基于斜坡单元的地质灾害气象预警系统建设初探
刘正华,余丰华,夏跃珍,佘恬钰,诸 烨
(1.中国地质大学(武汉)工程学院,湖北武汉 430074;2.浙江省地质环境监测院,浙江杭州 310007)
近年来,国内外学者对区域性降雨诱发地质灾害气象预警方法进行了大量的研究,使区域性地质灾害气象预警得到了较快的发展,并取得了良好的效果[1~5]。但这些研究主要集中在计算方法上,如临界降雨阈值法、信息量法、线性回归、神经网络等,预警单元也通常选用便于计算的网格单元,特别是大范围、小比例尺的情况。比如中国地质环境监测院采用地貌单元将全国划分为7个大区、28个预警区(2004年细化为74个区)建立了全国地质灾害气象预警系统。2008年采用10 km×10 km网格单元进行了升级[6]。各省省级预警系统也基本采用10 km×10 km网格单元,部分省采用5 km×5 km或1 km×1 km的网格。随着研究的深入,以网格单元或粗放的预警区为预警单元存在较多弊端。首先一个网格单元可能包含数个斜坡体,通常以最不利的影响因素值作为该网格单元特征值进行预测,结果表示该网格单元内各因素最不利的组合,与真实情况差距较大;其次预警对象也不明确,造成防御工作量增大,而采用斜坡单元则不存在这些问题。当前已有学者采用斜坡单元进行地质灾害研究,但多集中于单体斜坡稳定性数值计算或采用概化区域岩土参数进行斜坡稳定性数值计算[6~8]。
浙江省于2003年基于1 km×1 km的网格单元研制了地质灾害气象预警系统。但由于浙江省地质灾害规模小,往往发育于局部山坡地带,而1 km×1 km的网格范围大,涵盖多个方向坡面,无法确定究竟哪个坡面产生滑坡的可能性大,致使防灾对象无谓扩大,浪费人力物力。为完善浙江省地质灾害气象预警系统,提升地质灾害气象预警能力,浙江省地质环境监测院于2013年开始基于斜坡单元,采用联合概率模型研制省级地质灾害气象预警系统。
1 基于斜坡单元的地灾气象预警模型
降雨诱发地质灾害是概率事件,通常认为地质灾害发生的概率由以下两部分构成:一是地质环境内部条件形成地质灾害的可能性,即潜势度;二是降雨与地质环境相互作用增大了地质灾害发生的可能性。因此,地质灾害气象预警模型以潜势度为基底概率,以地质环境条件和降雨耦合作用促进地质灾害发生的可能性作为增量概率,构建地质灾害气象风险预警公式,计算预警指数,进行分级预警,模型可表达为:

式中:P——地质灾害发生概率,即预警指数;
P0——非降雨情况下地质灾害发生概率,即潜势度;
△P——降雨诱发地质灾害的增量概率;
G——与地质灾害有关的环境因子;
R——降雨量。
对2013年“菲特”台风强降雨期间发生的65起地质灾害与其前7日累计降雨量建立统计关系(图1),可以看出,地质灾害发生的频数与累计雨量总体上呈正相关,接近线性关系。

图1 累计雨量(7d)与地质灾害的关系图Fig.1 Relationship between the cumulative rainfall(7 d)and geological hazard
用R/Rmax去掉R的量纲,形成一个介于0至1的降雨量概率,其中Rmax是一个区域常量,表示该区域历史最大过程降雨量或更大值。为表达地质环境条件越好、引发地质灾害所需要的雨强或雨量就越大,地质环境条件越恶劣、较小的雨强或雨量就可能引发地质灾害的基本认识,再引入潜势度P0:

其中,k是调整系数,上式可以继续简化为:

从上式可以看出,相同降雨量下,潜势度大(小)的区域增量概率就大(小);同样地,相同潜势度区域内,降雨大(小)的区域产生增量概率也大(小)。从而得出联合概率预报预警计算公式:

式中:K——有效雨量影响系数;
R——有效雨量,包含前期和预报降雨。
假设当前时刻为t0,进行未来△t+时间段的地质灾害预报预警。首先,t0时刻的累计有效雨量可表示为:

式中:△t-——从计算开始到t0时刻的持续时间,通常为区域地质灾害与前期持续降雨时间的相关性最显著的时段,一般取24 h的整数倍,即若干天;
rc(t)——降雨过程雨量函数;
k(t)——有效雨量衰减函数,主要考虑大气降水对岩土体渗透过程以及地表径流等因素,一般取k(t)=kt,其中k是介0和1之间的经验系数,也可称为衰减系数。
其次,从t0时刻至未来△t+时段预报雨量可表示为:

式中:△t+——预报时段,由气象降雨预报时段确定,通常24h;
rf(t)——降雨预测过程雨量函数。
因此,建立地质灾害预报预警模型如下:

式中:K'——有效雨量调整系数;
Rc——有效累计雨量;
Rf——预报雨量;
L——预报雨量调整系数;
R'MAX——区域内一个预报预警期间的累计有效雨量与预报雨量之和的最大值。
根据地质灾害气象预警模型公式制作预警指数分布图(图2),即可根据预警指数分布情况发出黄色、橙色和红色预警,图中r=K'(Rc+LRf)。

图2 预警指数与潜势度和雨量关系Fig.2 Relationship of warning index and degree of potential and precipitation
2 浙江省级地灾气象预警系统建设
2.1 斜坡单元划分
斜坡单元是指由山脊线、山谷线、水系组成的封闭单元。斜坡单元的划分一般基于研究区域一定精度的DEM,采用水文分析模型。基本原理是利用正反地形分别提取汇水线和分水线,把生成的集水流域与反向集水流域融合,再经人工修改不合理的单元,最终得到的由汇水线与分水线所组成的区域即为斜坡单元。
基于此,采用浙江范围的NASA STRM DEM和浙江省1∶25万地形图,将浙江省山地丘陵地区划分为117 955个斜坡单元(图3)。

图3 浙江省斜坡单元图Fig.3 Slope unit in Zhejiang
2.2 潜势度的计算
潜势度是地质灾害“四度”指标之一[4],主要反映地质环境内部作用形成地质灾害的可能性。通常采用确定性系数模型(CF值)方法进行计算。本文中为避免潜势度值的过度分散,提出采用分类赋值的方法计算斜坡单元潜势度。
根据浙江省县市地质灾害调查与区划综合研究、小流域泥石流调查评价综合研究和降雨型滑坡预报理论方法及应用研究等成果,选择与地质灾害发生关系密切的地形地貌(高程、坡度、坡向、水系)、地层岩性(工程岩土类型)、地质构造、年均降雨、人类工程活动(交通、土地利用)等9个因子和8 251个地质灾害及隐患点参与计算潜势度[9],计算过程如下:
(1)根据地质环境因子状态,按照通用的分类方法或等间距分类方法将环境因子进行分类和量化,其中面状因子按照原有定性分类;线状因子根据缓冲区面密度分级,如构造、水系、交通根据缓冲区与单元面积的比值。
(2)利用Certainty Factors模型中CF函数计算每类数据的确定性因子CF,CF的变化区间为[-1,1]。当CF为正值时,表示地质环境条件差,发生地质灾害的确定性高;负值则表示地质环境条件好,发生地质灾害的确定性低;接近0时表示不能确定地质环境的优劣。

式中:CFij——第i个因子第j类的CF值;
P(H|Gij)——当 Gij的第 j类 Gij出现时发生地质灾害的条件概率;
P(H)=8251/105526.5,为区域地质灾害发生的先验概率。工程岩组的CF值见图4,其它图略。
(3)将每个因子各分段的CF值从+1到-1进行排序,并根据其值的范围将分段归纳为5类,反映该因子分段的地质环境优劣的5个级别,分别赋值0.1~0.5(表1)。
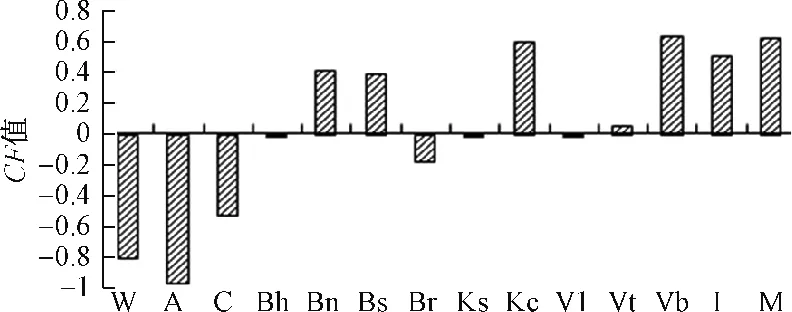
图4 工程岩组CF值Fig.4 The CF values of the rock group

表1 各环境因子分类及赋值Table 1 Environmental factors classificati on and assignment
(4)对每一个预报单元,利用Certainty Factors模型parallel-combination函数将各因子图层CF值逐步叠加合并,获得各因子的累计Z值。

(5)对Z值按照表2的分段意义进行分段统计,并将相邻两个因子Z值分段百分比两两相减,获得各因子分段百分比的变化量(图5)。

表2 CF分段统计说明Table 2 The CF value segmented statistic
(6)将各因子变化量的绝对值求和(T)作为分子,所有因子变化总量(∑T)作为分母,计算各个因子的权重(表3)。

图5 各因子图层Z值的变化量Fig.5 The Z value change of each factor

表3 各因子权重Table 3 The weight of each factor
(7)根据单元内各因素的等级属性,采用下式计算斜坡单元的潜势度,并绘制潜势度图(图6)。

式中:Wi——各因子权重;
Qij——坡面单元内因子分段值(表1)。

图6 浙江省灾害潜势度图Fig.6 The potential degree of geological hazard in Zhejiang
2.3 雨量数据处理
2.3.1 实测降雨数据处理
浙江省大部分地质灾害均在强降雨当天发生,而地质灾害发生前3天有降雨的占83.9%[9],前7日累计降雨与地质灾害发生数相关程度非常高(图1)。因此,本系统采用前7日降雨量进行计算。浙江省日降雨衰减系数通常取0.5~0.8[10],根据多年测试取0.7较合适,每个斜坡单元7日累计有效雨量计算方法如下:

前期降雨量由2 491个气象和2 457个水利部门的野外自动雨量监测站实测数据提供。通常以Excel文件定时提取后采用插值方法提取坡面单元降雨值,再计算预报日前7日累计有效降雨量。
2.3.2 预报降雨数据处理
预报降雨量由气象部门每日提供未来24小时图形预报和数值预报。图形预报采用人工交互矢量化方法提取斜坡单元预报雨量值;数值预报则采用插值的方式提取斜坡单元预报雨量值。
2.4 参数值的确定
2.4.1 预警预报分级指数的确定
通常认为自然斜坡在没有降雨的影响下发生地质灾害的可能性极小,即设定P0<0.5,当降雨作用产生概率增量与潜势度之和P≥0.5时,地质灾害才可能发生,因此设定0.5为黄色预警的下限值。而橙色和红色预警临界值可以根据图2确定。但预警区域划分受当地防灾能力限制,在实践中根据工作经验和防灾能力确定黄色、橙色、红色预警分级指数界线为0.5,0.75,0.90。
2.4.2 模型参数的确定
当进行24h预报时,预警指数模型为:

式中:K0——潜势度调整系数;
L——预报雨量调整系数;
e——修正系数。
K1=k/R'MAX,根据浙江省最大日降雨量为874.7 mm(2004年乐清市砩头站),累计7日有效降雨量小于1500 mm,因此,取R’MAX=2000,这是一个偏大的估计值,平常可通过测试进行调整。
选择区域内有代表性的地质灾害及隐患点坡面数据进行测试计算,确定24h预报预警模型参数K0=0.8、K1=0.005、L=0.004、e=0.1。
当进行6h/3h/1h短时预报时,现阶段短时预报雨量缺乏,即令Rf=0。预警指数模型为:

同理,可得模型参数 K0=0.8、K1=0.02、e=0.1。
3 预警结果检验
将2013年发生的509处地质灾害点分别采用新旧两个系统进行评价。为了消除降雨预报的误差,在评价过程采用次日实况降雨作为预报雨量。
测试结果显示:新系统漏报率和预报区面积明显减少,预报成功率和准确度显著提高,特别是梅汛期及台风期集中强降雨诱发地质灾害的预报成功率提升明显;但对于零星发生的地质灾害的预报成功率仍然较低,漏报情况也较多。总体上新系统预报区域针对性更强,成功率更高,明显优于原系统(表4)。
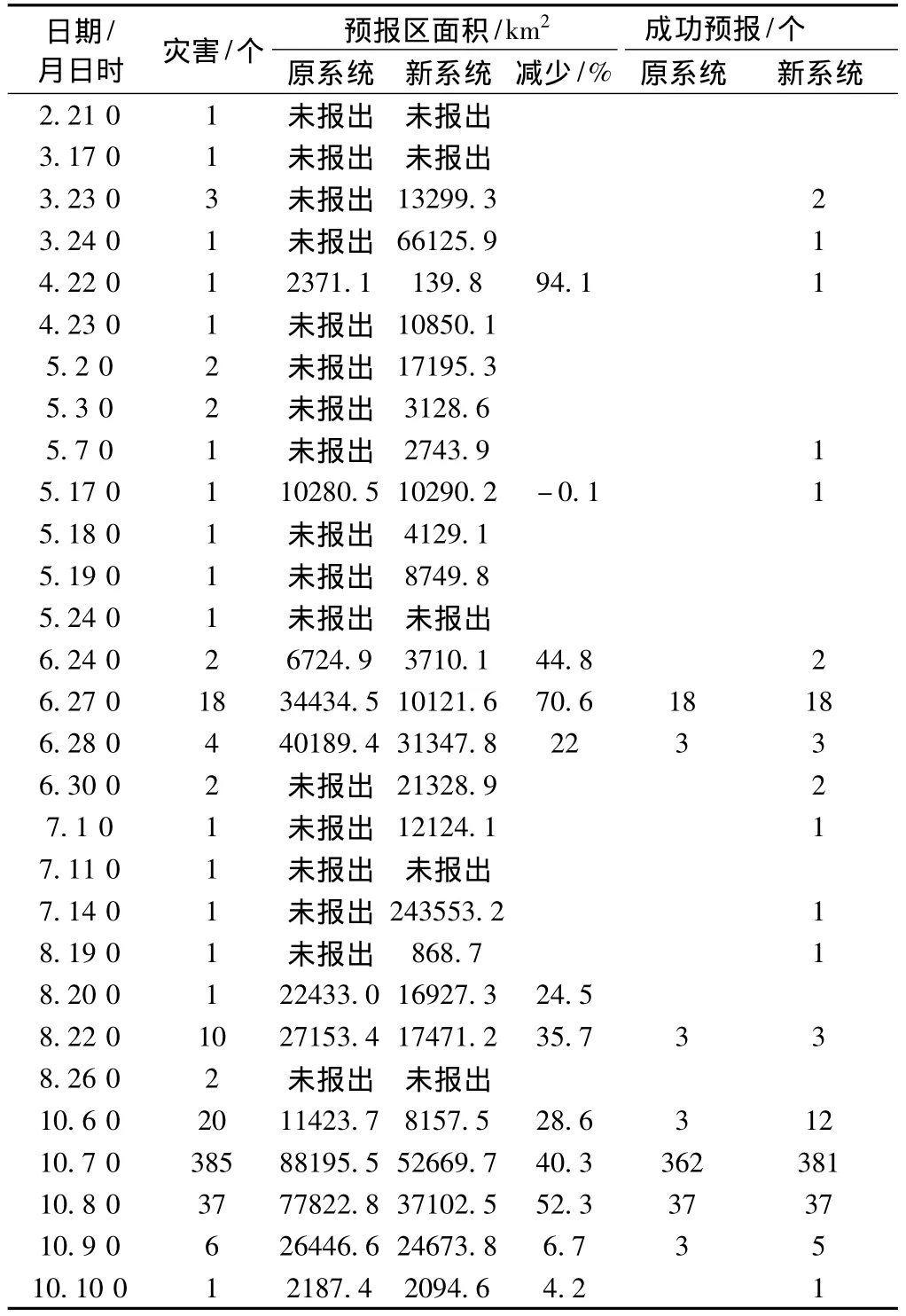
表4 测试结果对比统计Table 4 Comparision of the test results
4 结论与建议
(1)本文尝试在省级范围采用斜坡单元构建地质灾害气象预警系统,基于斜坡单元的概率统计方法不仅避免了区域斜坡稳定计算难于获取参数,也避免了概率统计对象的不准确性,是未来中、大比例尺开展地质灾害气象预警的趋势。
(2)地质灾害气象预警采用斜坡单元不仅清晰地反映了地质灾害与斜坡内在因素的关系,而且预警对象更明确,防治措施针对性强,比网格单元、地貌单元、流域单元、均一条件单元等具有明显的优势。
(3)预警模型采用非线性联合概率方法拟合地质环境条件与降雨耦合作用,计算预警指数,开展预报预警效果明显。对2013年全省地质灾害点进行测试表明,有效减少了预报区面积,在预报成功率上有较大的提升。
(4)测试结果表明本系统对集中强降雨引发地质灾害预警效果较好,而对零星降雨引发地质灾害预警漏报较多,有待进一步分类研究。
[1] Emmanuel J G,Douglas W B.Rainfall thresholds for landslide in the Himalayas of Nepal[J].Geomorphology,2004,63:131-143.
[2] Aleotti P.A warning system for rainfall-induced shallow failures[J].Engineering Geology,2004,73:247-265.
[3] Chowdhury R,Flentje P.Uncertainties in rainfall-induced landslide hazard[J].Quarterly Journal of Engineering Geology and Hydrogeology,2002,35:61-70.
[4] 温铭生,王连俊,李铁峰,等.云南省新平县滑坡预警区划研究[J].水文地质工程地质,2010,37(4):103-106.[WEN M S,WANG L J,LI T F.Earlywarning zoning studying of landslides in Xinping[J].Hydrogeology & Engineering Geology,2010,37(4):103-106.(in Chinese)]
[5] 陈玉萍,袁志强,周博,等.遗传算法优化BP网络在滑坡灾害预测中的运用研究[J].水文地质工程地质,2012,39(1):114-119.[CHEN Y P,YUAN Z Q,ZHOU B,et al.Application of back propagation neural networks with optimization of genetic algorithms to landslide hazard prediction[J].Hydrogeology & Engineering Geology,2012,39(1):114-119.(in Chinese)]
[6] 刘艳辉,刘传正,连建发,等.基于显式统计原理的地质灾害区域预警方法初步研究[J].中国地质,2008,35(2):344-350.[LIU Y H,LIU C Z,LIAN J F,et al.Method of Regional Early Warning of Geohazards Based on the Explicit Statistical Theory[J].Geology in China,2008,35(2):344-350.(in Chinese)]
[7] 谷天峰,王家鼎,付新平.基于斜坡单元的区域斜坡稳定性评价方法[J].地理科学,2013,33(11):1400-1405.[GU T F,WANG J D,FU X P.Regional slope stability analysis method based on the slope unit[J].Scientia Geographica Sinica,2013,33(11):1400-1405.(in Chinese)]
[8] 尚慧,倪万魁,程花.斜坡单元划分在彭阳县地质灾害危险性区划中的应用[J].中国水土保持,2011,9(3):48-50.[SHANG H,NI W K,CHENG H.Application of slope unit division to risk zoning of geological hazards of Pengyang county[J].Soil and Water Conservation in China,2011,9(3):487-50.(in Chinese)]
[9] 李长江,麻土华,朱兴盛.降雨诱发滑坡预报理论、方法及应用[M].北京:地质出版社,2008.[LI C J,MA T H,ZHU X S.Forecasting of Landslides Triggered by Rainfall: Theory, Methods&Applications[M].Beijing:Geological Publishing House,2008.(in Chinese)]
[10] 殷坤龙,张桂荣,龚日祥,等.浙江省突发性地质灾害预警预报[M].武汉:中国地质大学出版社,2005.[YIN K L,ZHANG G R,GONG R X,et al.Sudden geological hazard forecasting&warning in Zhejiang province[M].Wuhan:China University of Geosciences Press,2005.(in Chinese)]

