利用同余对数的整除性特征进行检验

赵云平

（滇西科技师范学院 数理系，云南 临沧 677099）

利用同余对数的整除性特征进行检验

赵云平

（滇西科技师范学院 数理系，云南 临沧 677099）

同余在数论里边是非常重要的一个内容，在初等数学中有广泛的应用。利用同余这一工具对数的整除性特征进行探讨，并详细给出了能被2、3、4、5、7、8、9、11、13、25、125等数整除的数的特征的检验，能让初学者更好地掌握相关数学结论。

同余；整除性；特征；检验

同余是数论中的重要概念，德国数学家高斯最先引用了同余的概念和符号，而同余理论是初等数论的重要组成部分，是研究整数问题的一种重要工具。在有的问题里边，我们经常会讨论某一个数除以另外一个数的余数是多少，而不管商到底是什么。比如说今天是星期二，再过20141000天是星期几？把20141000算出来就很难，再除以7找它的余数就更难，我们只考虑余数是多少不考虑商，没必要把商求出来，于是我们就要利用同余这个工具来找到这个余数。此外，利用同余还能简便的论证某些整除性的问题。在数论中有这么一个内容，利用同余检验因数，即利用同余对数的整除的特征进行验证，大多教材中仅例举了1～2个数的检验，在此我们对常用的数的检验进行详细说明。

1 预备知识、基本符号和概念[1,6]

定义1.1给定一个正整数m，把它叫做模（其实就是除法里的除数）。如果用m去除任意两个整数a和b，如果所得余数相同，则称a与b关于模m同余，记作。若a、b被m除余数不同，称与关于模不同余，记作。

定理1.2（反身性）对任意整数a有。

这是非常明显的事情，因为整数a除以m，得到的余数是唯一的。

2 利用同余检验因数

下面利用同余对数学中数的整除的特征进行一一检验，在利用同余检验因数的初始步骤要认真、准确的做出判断和选择，要选用什么样的进制：十进制、百进制、千进制等。其中十进制进率是10，从数的个位开始，每个数之间用逗号隔开；百进制进率是100，从个位开始两个数为一组用逗号隔开；千进制进率为1 000，从数的个位开始三个数为一组，依次用逗号隔开。这里把正整数a写成，上面加上一条线表示各位数码，用a0表示个位数码，a0对应的是相应进率的零次方，an就对应进率的n次方。如选择千进制，数2 536 429=2×1 0002+536×1 000+ 429，其中a0=429，a1=536，a2=2。

（1）能被2整除的数的特征是个位数字能被2整除（即个位为偶数）

就是说a能被2整除，则a0也能被2整除，即个位能被2整除（个位为偶数）。如取a=132=1×102+ 3×10+2，或取a=1346=1×103+3×102+4×10+6，或取a=3574=3×103+5×102+7×10+4，均能被2整除，因为这些数的个位都能被2整除，个位都为偶数。

（2）能被3（或9）整除的数的特征是各位数之和能被3（或9）整除

若能被3（或9）整除，则各位数字之和能被3（或9）整除。如取a=8 571 492=8×106+5×105+7×104+ 1×103+4×102+9×10+2，把各位数加起来8+5+7+1+ 4+9+2=36，36能被3整除，所以=8 571 492能被3整除；又36能被9整除，所以a=8 571 492也能被9整除。

(3)能被4（或25）整除的数的特征是这个数的末两位能被4（或25）整除

所以a≡a0（mod4（或25）），这里选择百进制，从个位起2个数为一组，故a0表示末两位，就是说如果a能被4（或25）整除，那么这个数的末两位也能被4（或25）整除。如取a=716=7×100+16，末两位16能被4整除，所以a=716能被4整除；取a=675=6× 100+75，末两位75能被25整除，所以a=675能被25整除。

(4)能被5整除的数的特征是个位数能被5整除（个位为0或5）

证明仿(1）

(5)能被7（或11或13）整除的数的特征是奇位千进位的和与偶位千进位的和的差（或反过来）能被7（或11或13）整除

其中

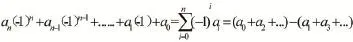
这里选择千进制，从个位起3个数为一组，a0表示末三位，依次类推。就是说如果a能被7（或11或13）整除，那么这个数的奇位千进位的和与偶位千进位的和之差也能被7（或11或13）整除。如取a= 8 949 682=8×1 0002+949×1 000+682，又949-（682+8）=259,259能被7整除，所以a能被7整除；取a=6022766321=6×10003+22×10002+766×1000+ 321，又（766+6）-（321+22）=429，429能被13整除，所以a=6 022 766 321能被13整除。

对于11的判断，还可选用10进制，即

因10≡-1（mod11），

由推论1.3.2，10k≡（-1）k（mod11），

由定理1.2，ak10k≡ak（-1）k（mod11），

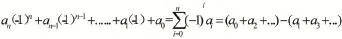
虽然得到的式子一模一样，但此刻选择的是10进制，即从个位开始每一个数为一组，用逗号隔开，此时的a0表示个位，a1表示十位，以此类推。能被11整除的数的特征还可描述为：奇数位之和与偶数位之和的差能被11整除。如取a=82159＝8×104＋2×103＋1×102＋5×10＋9，（9+1+8）-（5+2）=11,11能被11整除，所以82 159能被11整除。

（6）能被8（或125）整除的数的特征是这个数的末三位能被8（或125）整除

因1 000≡0（mod8（或125）），

由推论1.3.2，1000k≡0k（mod8（或125）），

由定理1.2，ak1000k≡ak0k（mod8（或125）），

所以a≡a0（mod8（或125）），这里选择千进制，从个位起3个数为一组，故a0表示末三位，就是说如果a能被8（或125）整除，那么这个数的末三位也能被8（或125）整除。如取a=76 432＝76×1 000＋432，末三位432能被8整除，所以a=76 432也能被8整除；如取a= 89 294 375=89×1 0002+294×1 000+375，末三位375能被125整除，所以a=89 294 375能被125整除。

3 结语

同余与整除有着密不可分的联系，我们讨论的整除只是考虑了余数为0的情况，而同余是要进一步考虑余数是其它的任意一个，比如说被b除，余数小于b的情况。利用同余检验整除性特征，再次证明了数学结论的正确性与可行性。同余与整除的结合，让初学者从中感受到了数学的不变与多变性，不变的是数学结论，多变的是证明判断数学结论的依据，在数学领域中这样的例子还很多，值得我们进一步挖掘与探讨。

注释及参考文献：

[1]潘承洞,潘承彪．初等数论[M]．北京：北京大学出版社,2002:97-105．

[2]刘合义．谈数论中的同余及其应用[J]．衡水师专学报,2002,4(1):38-39．

[3]张中峰．同余理论的一些简单应用[J]．肇庆学院学报,2013,34(2):8-11．

[4]朱丽平．关于同余的几个问题[J]．高师理科学刊,2008,28(5):43-46．

[5]李为善．同余的一个应用[J]．镇江高等专科学校学报,2000,13(4):80-81．

[6]闵嗣鹤,严士健．初等数论[M]．北京:高等教育出版社,2003:48-53．

[7]木仁,韩荣梅,张昆龙．同余关系的一些性质[J]．赤峰学院学报(自然科学版),2005,21(4):1-2,5．

[8]李山林．数的整除特征的探讨[J]．内蒙古电大学刊,2006,86(10):90-91．

Test Aliquot Sexual Characteristics Using the Congruence of Logarithmic

ZHAO Yun-ping
(Department of Mathematics and Physics,Dianxi Science and Technology Normal University,Lincang,Yunnan677099)

Congruence in number theory is a very important content,which has wide application in elementary mathematics.By using congruence,the characteristics of numbers divisibility are discussed in this paper,and presents test of the number characteristics that can be divisible by 2,3,4,5,7,8,9,11,13,25,125 etc,to make scholars better master relevant mathematical conclusion.

congruence;divisible;characteristic;inspection

O156.1

A

1673-1891（2015）04-0019-03

2015-09-08

赵云平（1982-），女，硕士，讲师，研究方向:基础数学数论应用、应用数学运筹学线性规划、数值代数。