基于嫦娥三号软着陆目标区域选取的研究*

李峻山，赵婉茹，许梦宇，朱家明

（安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030）

基于嫦娥三号软着陆目标区域选取的研究*

李峻山，赵婉茹，许梦宇，朱家明

（安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030）

针对嫦娥三号探月卫星运行过程，主要探究嫦娥三号软着陆过程中着陆目标区域的选取。根据不同地域所拍摄照片像素点数值大小不同的特性，通过构造、计算平坦系数并建立合适的空间直角坐标系，从而找出相对平坦区域，根据路径最小原则，选取嫦娥三号的最佳着陆地点，并给出相应的轨迹方程。

嫦娥三号；软着陆；灰度图像矩阵；MatlabR2010b；平坦系数

发射人造地球卫星、载人航天和深空探测是人类航天活动的三大领域。重返月球、开发月球资源、建立月球基地已成为世界航天活动的必然趋势和竞争热点。开展月球探测工作是我国迈出航天深空探测第一步的重大举措。实现月球探测将是我国航天深空探测零的突破。月球已成为未来航天大国争夺战略资源的焦点。本文以2014年全国大学生数学建模竞赛A题[1]为例，以嫦娥三号探月卫星为研究对象，通过Matlab编程，来研究嫦娥三号软着陆过程中的粗避障、精避障阶段的着陆目标选取。

1 研究准备

1）对新名词的解释：平坦系数(d)：利用平面灰度图像矩阵(Gmn)计算出的用以描述平面平整度的系数，数值越小表示平面越平坦。其具体计算公式如下：

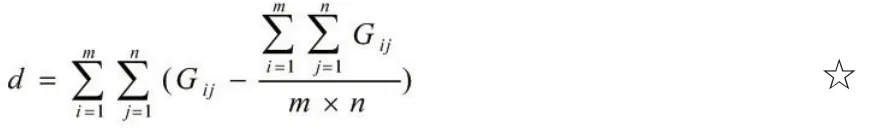
Amn表示平面灰度图像矩阵

2）坐标系的建立：以飞船所拍摄照片的中心（月球的19.51W，44.12N）为坐标原点，竖直向上为z轴，x,y轴分别建立在数字高程图中所显示的水平面上并与图片边缘平行，坐标系建立结果如图1所示。

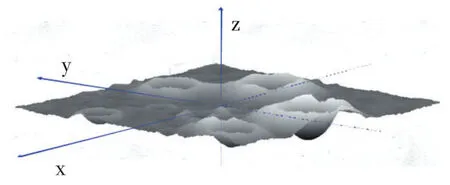
图1 坐标系的建立

2 粗避障阶段的分析与求解

2.1 粗避障阶段的分析

在粗避障阶段要求我们避开较大的陨石坑，也就是说我们应该把飞船引导向尽量平坦的地区降落，我们通过2 400 m高度拍摄的灰度图像寻找平坦区域，根据灰度图像矩阵数值大小可以反映地理相对高度大小的特性，我们对灰度图像矩阵进行分块[2]，计算每一个分块矩阵的平坦系数，这样我们只要把飞船引导向平坦系数最小的区域即可。距月面2 400 m处的数字高程照片如图2所示。

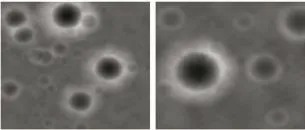
图2 距月面2 400 m（左）和100 m（右）处的数字高程图

2.2 挑选粗避障的着陆目标区域

选取合适的分块矩阵大小：

在粗避障阶段拍出的数字高程图的水平分辨率是1 m/像素，其数值的单位是1 m,矩阵大小是2 300×2 300；而在距月面100 m拍出的数字高程图的水平分辨率为0.1 m/像素，数值单位是0.1 m，大小是1 000×1 000；为了与精避障阶段的研究联系起来，在现阶段我们选择100×100作为一个单位分块矩阵大小。

计算平坦系数秩序矩阵：

第一步：用Matlab将（距2 400 m处的数字高程图）图像读入[3]后得矩阵：

第二步：挑取出矩阵A中的每一个100×100矩阵：

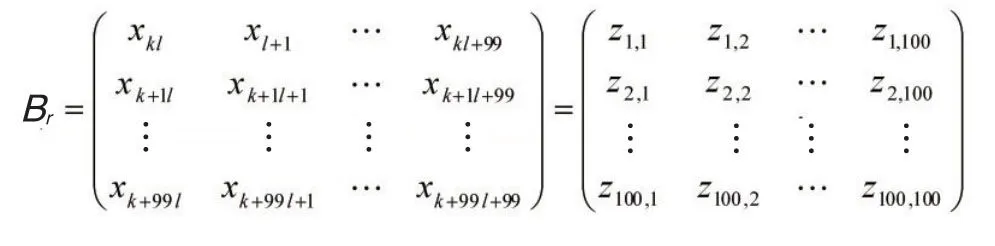
对D排序得秩序矩阵D'[4]，那么合适的降落区域也必定在平坦系数秩序矩阵中排名靠前的平坦系数所对应的区域中产生，由于陨石坑都呈现倒锥状，所以不可能出现区域位于坑底或坑顶而平坦系数计算值较小的情况。

按照以上算法利用Matlab求解出2 400 m处数字高程图的平坦系数如表1所示。

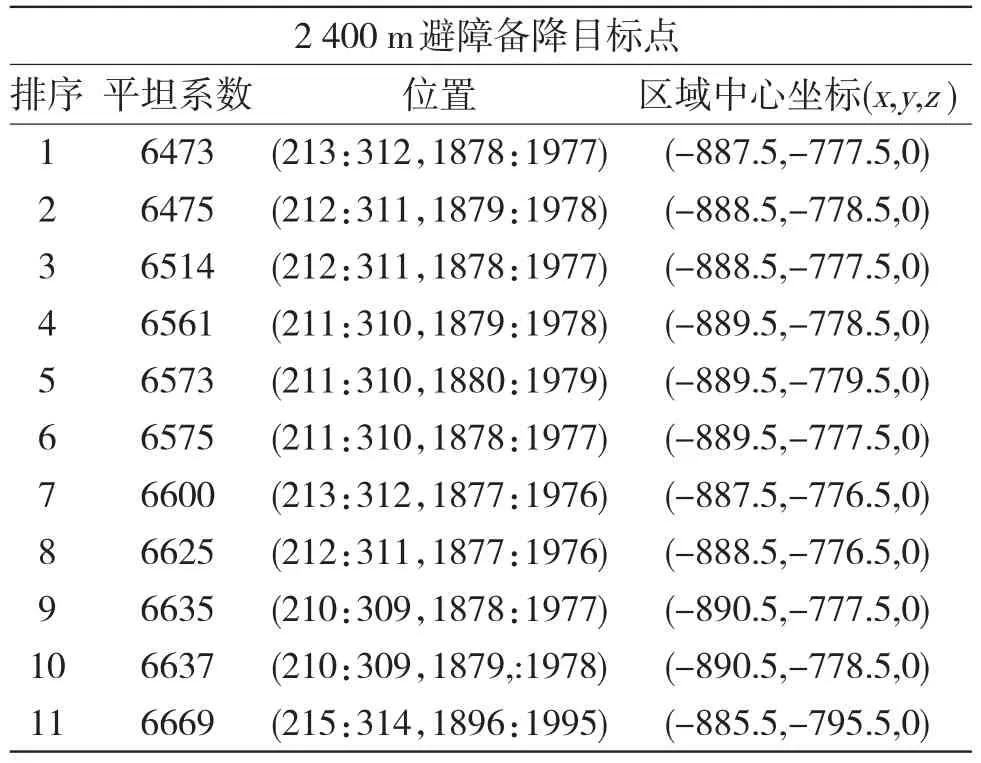
表1 2 400 m处数字高程图的平坦系数

关于表1中数据的意义，我们做以下说明：

（1）位置：表示该平坦系数对应的子矩阵所在灰度图像矩阵中的行列位置，比如(213∶312，1 878∶1 977)指平坦系数为6 473的那个100×100子矩阵在原矩阵中的第213至312行，1 878至1 977列。

（2）区域中心坐标：表示该平坦系数对应的子矩阵所表达的子灰度图像投影在三维坐标系的x，y坐标平面上的中心坐标。

2.3 求解最佳着陆点

根据上述解法，在秩序平坦系数矩阵中排在第一位的平坦系数所对应的区域就是降落目标区域，但是考虑到飞船自带的燃料有限，在避障阶段消耗的燃料越多飞船的着陆失败风险就越大，根据坐标图和实际经验容易知道飞船选取的着陆目标偏离空间坐标系轴越远，其所行走的路程就消耗越多燃料，所以在降落区域的选取上，我们可以在可行的降落区中选择区域中心与原点的欧式距离最小的降落去作为最佳降落区。

假设飞船的自控范围为平坦系数＜H且H= 6 635，根据平坦系数秩序矩阵挑选出的可降落区为，每个可行降落区的的中心坐标为，那么每个可行降落区的中心与原点的欧氏距离[5]为：

由表1数据计算得出降落区域的平坦系数与欧氏距离如表2，欧式距离折线如图3所示。

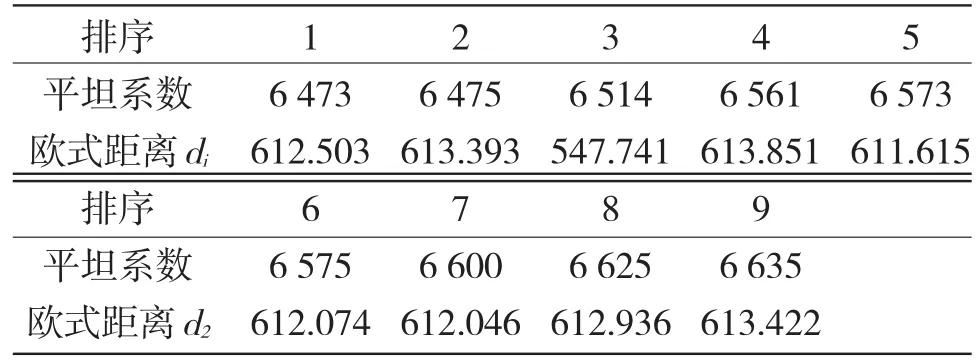
表2 降落区域的平坦系数与欧氏距离

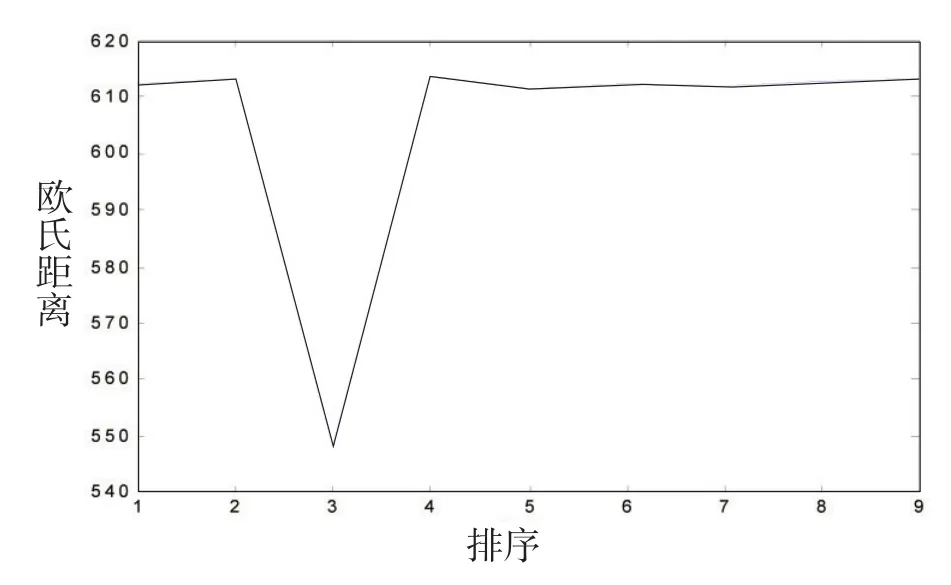
图3 欧式距离折线图

2.4 确定避障飞行轨迹

利用上一个模型中确定的合适降落区域为S,可以确定其对应矩阵在原灰度图像矩阵中是在第g至 g+99行，第h至h+99列即，从而可以确定该区域的中心坐标为，在其100 m正上方的对应坐标为，再有飞船在2 400 m高空时的坐标为（0，0，2 400）,可以根据这2个点确定一条直线，可计算其轨迹方程[6]为：

这也就是飞船在粗避障阶段的飞行轨迹。

根据欧式距离最小原则可以看出选取排序为3平坦系数为6 514的区域为着陆点最合适，那么在其上方100 m处对应坐标为(-888.5,-777.5,100)，根据公式（1），求得粗避障阶段的飞行轨迹方程为：

嫦娥三号应该通过控制自身发动机沿着该直线飞行，飞行轨迹如图4所示。

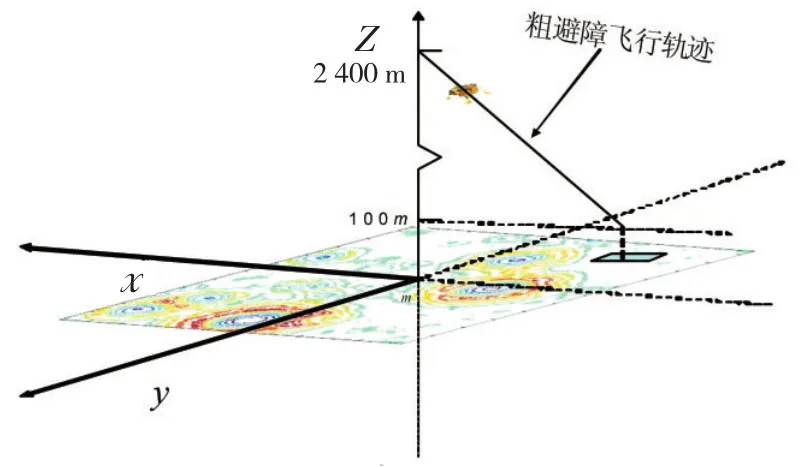
图4 嫦娥三号的粗避障阶段飞行轨迹

3 精避障阶段的分析与求解

精避障阶段要求精细避开月面障碍物，也就是要求在可视范围内选择最平坦的区域作为飞船的着陆点，所以这里可以利用和粗避障阶段相同的模型，通过计算平坦系数来量化选择最佳着陆点。在此阶段我们选取40×40为一个分块矩阵大小。主要是基于以下原因：嫦娥三号降落区域面积不到16 m2（嫦娥三号着陆器的底面是长宽不到4 m的近似长方形），当嫦娥三号悬停在100 m高空时拍摄的图像是0.1 m/像素，那么反映在图像矩阵中一个40×40的像素点阵表示的实际月面面积就是16 m2，故而我们选取40×40为一个分块矩阵大小。

求得100 m精避障阶段的相应数据如表3、表4和图5所示。

表3 位于100 m处平坦系数

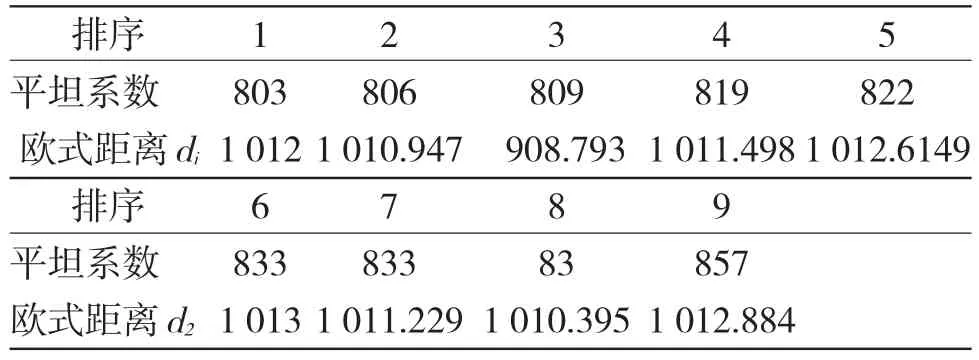
表4 降落区域的平坦系数与欧氏距离

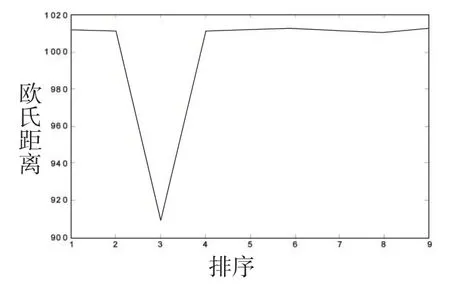
图5 欧式距离折线图

根据欧式距离最小原则可以看出选取排序为3平坦系数为809的区域为着陆点最合适，那么在其上方100 m处对应坐标为(-844,-337)，根据公式（1），求得精避障阶段的飞行轨迹方程为：

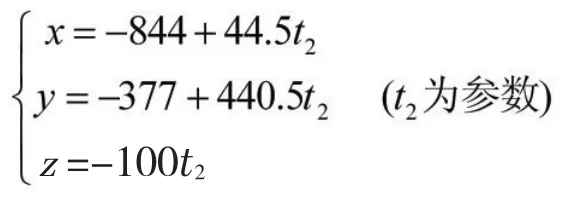
飞船应该通过控制自身发动机沿着该直线飞行，那么嫦娥三号登月飞船在粗避障和精避障阶段的运行轨迹如图6所示。

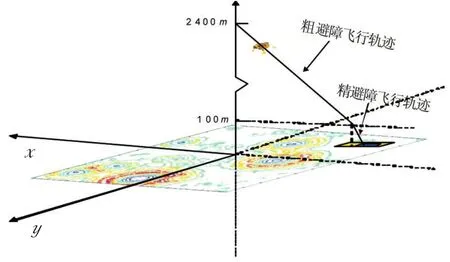
图6 嫦娥三号精避障阶段运行轨迹

4 结语

本文所介绍的嫦娥三号着陆目标区域选取方法利用了现代计算机快速精确计算优点，并且创造性地提出了平坦系数这一衡量平面平坦程度的概念。在模型中我们考虑到了所有的可能备降区域，给出一个精确的量化选择着陆区的方法。这种方法不仅适用于嫦娥三号的着陆，对现实中其他的航空航天器在未知区域安全降落同样具有重要意义。

注释及参考文献：

[1]2014全国大学生数学建模竞赛A题[EB/oL]．http://www．mcm．edu．cn/．

[2]王萼芳,石生明．高等代数[M]．北京:高等教育出版社，2012:181-186．

[3]张岩．Matlab图像处理超级学习手册[M]．北京:人民邮电出版社,2014:80-93．

[4]吴礼斌,闫云侠．经济数学实验与建模[M]．天津:天津大学出版社．2009:27-44．

[5]吴成东,贾子熙,张云州,等．基于欧氏距离的分布式网格定位估计方法[J]．东北大学学报,2013,30(3):1-3．

[6]吕林根,许子道．解析几何[M]．北京:高等教育出版社,2012．5:112-119．

The Landing Target Region Selection Based on the Chang'e No.3

LI Jun-shan，ZHAO Wan-ru，XU Meng-yu，ZHU Jia-ming
(School of Statistics and Applied Math，Anhui University of Finance and Economics，Bengbu,Anhui 233030)

Aim ming at the process of the Chang'e 3 lunar exploration project,this paper,mainly studies to select the object region in the process of Chang'e 3 soft landing.According to characteristics that pictures photoed in different areas have different sizes of the numerical pixel,it will be established a suitable space rectangular coordinate system and find out a relatively flat areas by construting and calculating flat coefficient.and select the best landing point of Chang'e,and conclude a corresponding trajectory equation under the principle of the minimum path.

Chang'e 3;soft landing;gray scale image matrix;matlab R2010b;flat coefficient

V525

A

1673-1891（2015）04-0022-03

2015-10-14

安徽财经大学教研项目（acjyzd201429）。

李峻山（1993-），男，安徽淮南人，研究方向：信息与计算科学。