固体火箭发动机喷管瞬态流场特性分析

徐学文，牟俊林，任建存，单 鑫

（海军航空工程学院,山东 烟台264001）

0 引言

固体火箭发动机喷管是将燃烧室内高温高压燃气所含有的一部分的能量转变为气体动能，从而使飞行器获得推力的机械装置，在导弹飞行条件和发动机工作状态一定的条件下，喷管的结构参数直接决定喷管的工作状态（欠膨胀状态、完全膨胀状态或过膨胀状态），从而决定了发动机推力大小和推进效率的高低。因此，开展固体火箭发动机喷管流场特性分析，使喷管更好、更有效地发挥其能量转换作用，这对喷管工程应用实践和进一步的优化结构设计具有指导意义。

当前，喷管流场特性分析一般采用实验研究和计算机仿真手段，而实验研究大多采用冷场研究[1-2]，这与喷管实际工作中的流场特征还有很大差别，因此计算机仿真就成为主要的研究手段，特别是许多大型商用CFD软件如FLUENT和PHOENICS等的出现。在计算机仿真中，国内大多计算模型仅以喷管流场为研究对象，喷管进口边界条件也只由热力学滞止状态参数（总温T0和总压p0）确定[3-5]，不考虑喷管实际工作过程中上游流场－燃烧室对喷管流场的影响。本文以某型固体火箭发动机喷管为研究对象，为准确预测发动机喷管的流场特性，考虑发动机工作过程中燃烧室流场对喷管流场的影响，因此，建立了燃烧室-喷管一体化三维流场模型[6-9]，仿真计算发动机点火启动过程中喷管内瞬态流场特性。

1 数值计算模型

1.1 流场模型

所研究的固体火箭发动机喷管为拉瓦尔喷管，燃烧室形状为五角星型，其头部安装有篓式点火器，燃烧室仅作为喷管流场进口边界条件的产生部件，在发动机点火启动过程仿真计算中，将燃烧室与喷管作为一个整体，所建立的喷管-燃烧室一体化三维流场物理模型如图1所示。模型中发动机燃烧室轴线为直角坐标系的x轴，方向指向发动机喷管，中心原点位于发动机头部轴线的起点上，由此表示流场横截面的位置。

图1 某固体火箭发动机燃烧室-喷管一体化流场模型Fig.1 The integrated flow field model of chamber and nozzle of the solid rocket motor

为便于计算，仿真中不考虑流场和固相之间的耦合，燃烧产物遵循完全气体状态方程，燃烧室药柱壁面按平行层规律燃烧，不考虑药柱的侵蚀燃烧效应和燃气辐射传热的影响。

1.2 计算方程

流场控制方程采用三维可压粘性方程，湍流模型采用计算精度比较高的应用比较广泛的k-ε二方程模型，另外，为使方程组封闭，还要补充气体状态方程。

1.3 初始和边界条件

1.3.1 初始条件

以固体火箭发动机点火器点火向燃烧室喷射燃气的时刻为流场仿真的计算起点，此时，燃烧室内和喷管内气体的压力、温度为周围大气的压力和温度。

1.3.2 流场壁面边界条件

喷管壁面和燃烧室内在被点燃之前的药柱面为流场的壁面边界，由于在近壁区域，燃气的流动情况受壁面影响比较大，燃气粘性力和湍流切应力在每个子层所主导的地位不一样，求解规律也不一样，本文采用壁面函数法[10]来求解近壁区域物理量。

1.3.3 质量进口边界条件

把燃烧室头部点火器的壳体表面作为燃烧室质量进口边界条件来确定，并假设点火器的单位面积质量流率沿整个壳体表面均匀分布，燃气流向垂直于壳体表面。当燃烧室装药表面的某点达到着火温度被点燃后，燃气开始从该点处向燃烧室内喷射，此处的壁面边界条件变为质量进口边界条件，给定入口单位面积的质量流率，即：

式中：ρprop为推进剂的密度；r为推进剂的燃速。

1.3.4 固相传热边界条件

在喷管壳体和燃烧室药柱壁面上均按第三类传热边界条件给出，即：固相壁面导热量等于流场表面传热量。

1.3.5 喷管出口边界条件

喷管出口边界条件按压力出口边界条件给出，当喷管出口处燃气流速为亚音速时，给定喷管出口上的背压力；当喷管出口处燃气流速达到超音速时，无须给定喷管出口上的任何参数，出口处的参数由内部流场参数推得。

2 计算结果及分析

采用有限体积法来离散喷管-燃烧室一体化三维流场模型，应用隐式的一阶迎风格式来离散控制方程，采用simple算法求解差分方程，仿真计算出发动机点火启动过程中喷管内燃气流场分布。

2.1 燃气亚音速流动阶段

发动机点火启动后，从燃烧室头部的点火器喷出高温高压燃气，燃气火焰锋和压力波开始向燃烧室四周及下游传播。在传播过程中，燃气压力波锋明显超前火焰锋，燃烧室内的空气受到压力波的扰动而压力升高，而温度还未升高。0.3 ms时燃气火焰锋到达燃烧室星根，开始加热星根处推进剂，药柱壁面受热面积逐渐扩大。0.9 ms时在燃烧室轴向0.08～0.14 m处的星根壁面上某些点处推进剂经过热量的积累达到着火温度开始燃烧，燃烧室头部压力升高，燃气压力波向下游传播速度加快。

1.5 ms时，燃气压力波到达喷管入口处（0.774 m），如图2所示，燃烧室内气体压力从头部到喷管呈单调下降趋势，而逐渐接近外界气压；燃气火焰锋在燃烧室轴向传播的距离为0.22 m，在火焰锋处突然降温；燃气火焰锋向前传播过程中先增速，在0.12 m处达到最高速度，然后速度迅速下降；在火焰锋前方，燃烧室内气体受火焰锋加热温度的影响越来越低，根据速度公式，压力波沿轴向传播速度也逐渐降低，但下降幅度比较平缓；燃气压力、温度及速度的这种变化趋势直至2.2 ms时燃气压力波锋到达喷管出口。

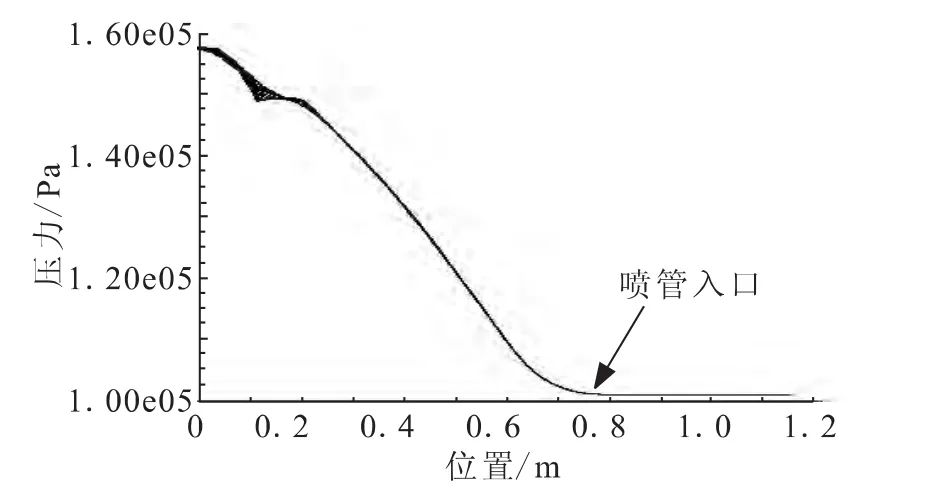
图2 1.5 ms时压力沿轴向变化曲线Fig.2 Change curves of pressure along axial direction at 1.5 ms

2.7 ms时燃气火焰锋到达燃烧室中部，燃烧室内燃气压力升高，并沿轴向分布趋向平缓，在喷管内，燃气流动速度增大，但仍为亚音速，在喉部之前燃气加速，在喉部马赫数达到最高值，但小于1，在喉部以后燃气减速，如图3所示；燃气压力在喷管内沿轴向仍呈单调下降趋势，喷管内还未产生激波，这种变化过程一直持续到燃气在喉部达到音速之前。

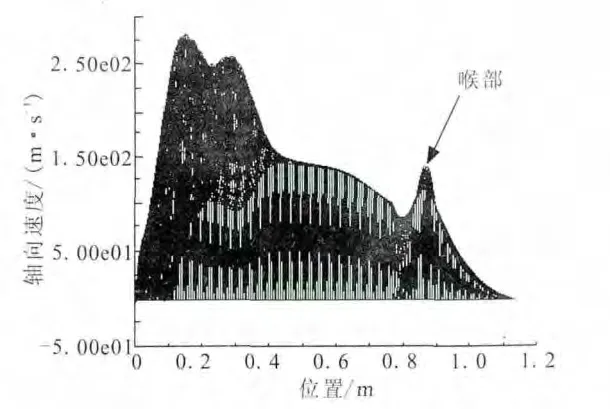
图3 2.7 ms时轴向速度沿轴向变化曲线Fig.3 Change curves of axial velocity along axial direction at 2.7ms

2.2 燃气壅塞流动阶段

随着燃烧室内燃气压力越来越高，喷管的进出口压力比也越来越高。3.4 ms时在喷管喉部燃气的流动速度达到临界速度，此时马赫数Ma=1，但速度在喉部之后又迅速下降；此时喷管进出口压力比为2.165，燃气压力在喷管喉部之前呈下降趋势，但在喉部之后压力稍稍升高再趋向于喷管出口背压——外界大气压。

3.8 ms时，燃气在喷管喉部之前亚音速加速流动，在喉部达到音速，在喉部之后燃气超音速加速一段距离之后突然减速流动，如图4(a)所示，这是说明在喷管扩张段出现了一道激波，正是由于激波的存在，使得燃气在喷管流动中压力在激波之前一直处于下降趋势，遇到激波后压力上升，而后又趋向出口处外界气压，如图4(b)所示，此时，喷管进出口压力比为9.19，喷管内燃气流动出现壅塞。

图4 3.8 ms时马赫数和压力沿轴向变化曲线Fig.4 Change curves of Mach number and pressure along axial direction at 3.8ms

同样，根据喷管一维等熵流函数也可证明喷管内此时出现了一道激波。已知喷管出口截面积A2和喉部截面积A*之比为：A2/A*=7.3 382；出口背压为：p2=1.01e5 Pa；喷管喉部处燃气的滞止压力为：po=1.06e6 Pa。根据连续方程，对于喷管内等熵壅塞流动有：

根据喉部Ma=1，查等熵函数表[11]并计算可得：当喷管出口截面上为亚音速时（即文特利管流）p2=1.057e6 Pa；当喷管出口截面上为超音速时p2=1.245e4 Pa，此时出口截面上的气体压力均不等于出口背压1.01e5 Pa，并且相差很大，因此在喷管喉部和出口截面之间必定有一道正激波存在。

2.3 燃气超音速流动阶段

随着燃烧室内燃气压力的升高，燃气在喉部之后超音速加速的距离不断扩大，激波在喷管内不断向外移动，燃气压力在喷管内仍呈现出先下降，然后突升，再下降至外界气压的趋势。

4.4 ms时，燃气速度在喷管内流动过程中持续增大，在出口处达到最大值，平均马赫数为3.39，喷管内无激波存在，如图5(a)所示；燃气压力在喷管内呈单调下降趋势，但愈靠近喷管出口处压力变化愈平缓，如图5(b)所示，喷管进出口压力比为15.47。此后，喷管内燃气速度和压力按这种变化规律一直增加到稳定状态为止。

图5 4.4 ms时马赫数和压力沿轴向变化曲线Fig.5 Change curves of Mach number and pressure along axial direction at 4.4 ms

根据喷管一维等熵流函数以及喷管A2和A*之比算得的喷管此时出口马赫数为：Mat=3.57，计算结果与理论分析结果比较相符。

3 结论

1）在药柱点燃初期，燃气压力波锋先于火焰锋到达喷管，喷管内燃气呈现亚音速流动，压力沿轴向呈单调下降趋势，喷管内无激波产生。

2）随着燃烧室压力升高，喷管内燃气呈现壅塞流动，在扩张段出现了一道激波，燃气压力在喷管内呈现出先下降，然后突升，再下降至外界气压的变化趋势。

3）随着时间推移，燃烧室内燃气压力逐渐达到稳态，喷管内燃气在喉部之后超音速加速的距离不断扩大，激波逐渐移出喷管外，最终，在喷管扩展段燃气呈现超音速流动，压力在喷管内呈单调下降趋势，喷管内燃气流动顺畅。

[1]丁英涛,谢君堂,仲顺安.微型喷管内气体流动的流量壅塞现象[J].北京理工学学报,2006,26(12)：1086-1089.

[2]张修峰,杨立,宋智勇.喷管通道内气体流动特性的实验分析与数值模拟[J].机电工程技术,2010,39(4)：25-28.

[3]刘君,郭健.双斜喷管固体火箭发动机流动特性数值模拟[J].固体火箭技术,2002,25(1)：8-9.

[4]黄宏艳,王强.过膨胀状态下轴对称收-扩喷管内外流场计算及分析[J].航空动力学报,2007,22(7)：1069-1073.

[5]罗静,王强,额日其太.轴对称矢量喷管内流特性的不同湍流模型计算[J].推进技术,2003,24(4)：326-329.

[6]赵汝岩,隋玉堂,周红梅.具有潜入式喷管的翼柱形药柱发动机火焰传播过程研究[J].固体火箭技术,2010,33(6)：526-630.

[7]杨乐,余贞勇,何景轩.基于FLUENT的固体火箭发动机点火瞬态内流场仿真影响因素分析[J].固体火箭技术,2011,34(4)：474-477.

[8]WILLIAM A D,MICHAEL T H,ROBERT A F.Integrated 3-D simulation of solid propellant rockets,AIAA 2001-3949[R].USA：AIAA,2001.

[9]FIEDLER R,JIAO X,NAMAZXIFARD A.Coupled fluid-structure 3-D solid rocketmotorsimulations,AIAA2001-3549[R].USA：AIAA,2001.

[10]VERSTEEG H K,MALAASEKERAW.An introduction to computational fluid dynamics-The Finite Volume Method[M].Beijing：Beijing World Publishing Corpration.2000.

[11]苏长荪.高等工程热力学[M].北京：高等教育出版社,1987.