马赫数2.5~7.0的二元变几何进气道设计
李永洲,刘晓伟,张蒙正,南向军
(西安航天动力研究所,陕西西安710100)
0 引言
火箭基组合循环(Rocket Based Combined Cycle,RBCC)发动机是高超声速飞行器和天地往返运输系统的理想动力装置[1-6]。相对TBCC和ATR等其他组合推进系统,RBCC发动机具有更宽的飞行空域、速域以及多种工作模态,其中模态间的平稳过渡是其稳定工作的前提,也是研制的难点[7]。进气道作为其关键部件,寻求适应上述要求的设计方案至关重要。
对Ma=4.0~7.0的双模态冲压发动机,由于定几何进气道结构简单,高低马赫数时的性能协调相对容易实现,因而普遍采用定几何方案[8]。但是,随着工作马赫数范围的拓宽,定几何进气道难以解决高、低马赫数下总体性能与低马赫数下起动性能之间的矛盾,变几何方案是必然的发展趋势。一些典型的高超验证飞行器都使用了变几何结构,如美国X-43A采用转动唇口形式[9],法国LEA采用斜向平移唇口设计[10]。对于更宽范围工作的RBCC发动机进气道,GTX发动机采用移动锥形中心体变几何方案并进行了进气道缩比实验[11]。美国Aerojet公司提出的Sturtjet发动机进气道通过转动整个顶板来调节喉道的面积以适应宽范围工作[12]。日本JAXA的RBCC发动机采用顶板上下平移方案[13]。国内张浩等针对内置中心支板的二元进气道[14],通过转动唇口、调节肩部型面以及设置放气槽实现了Ma=2.4~7.0正常工作。
总体看来,国外RBCC进气道变几何方案有限,国内更是起步较晚,因此亟需开展宽范围工作的RBCC发动机进气道变几何方案研究。二元进气道作为一种主要的进气道类型,设计方法成熟,利于与前体一体化设计,也容易实现变几何。本文针对矩形流道的RBCC发动机,研究了Ma=2.5~7.0的二元进气道变几何方案并通过数值仿真手段研究了其总体性能与调节方法。
1 变几何进气道设计
变几何进气道设计流程:首先,根据设计要求选择合适的设计马赫数与内外压缩面的角度完成基准进气道设计;其次,采用合适的变几何方案来满足低马赫数时总体性能和起动要求;最后,确定最终的调节方法来实现整个工作范围内高性能。
针对本文的变几何进气道,将其分为2段工作:高马赫数段 Ma=4.0~7.0和低马赫数段Ma=2.5~4.0,在这2段工作范围内,尽可能得保持型面固定。设计进气道基准构型时,考虑到高马赫数时处于冲压模态,设计马赫数取6.0。为了使进气道具有较高的流量系数,采用来流马赫数由高到低,外压激波依次封口的设计概念。图1给出了设计的基准进气道,第一级压缩角取6°,第二级压缩角取5°,第三级取6°来减小内压段长度,唇罩内型面后段是一段6°的上凸圆弧以弥散反射激波,优化喉部流场结构。第一道激波在Ma=6.0封口,第二道激波在Ma=5.0封口,第三道激波在Ma=4.0封口。此时,基准进气道的总收缩比Rct=6.6,内收缩比Rci比常规的定几何进气道显著增大,Rci=2.07,等直隔离段长度为7倍的喉道高度。

图1 变几何进气道基准气动构型Fig.1 Reference aerodynamic configuration of the variable geometry inlet
在低马赫数范围内(Ma=2.5~4.0),一方面进气道的压缩量需求减小,另一方面必须减小内收缩比来保证自起动能力。在基准构型的基础上,转动第三级以后的顶板是一种可行设计方法,这样既可以增大喉道从而减小了总收缩比和内收缩比,而且减小第三级压缩角也可以提高低马赫数的流量系数。本文将顶板沿第三级转折点A顺时针转动3.7°,见图2。
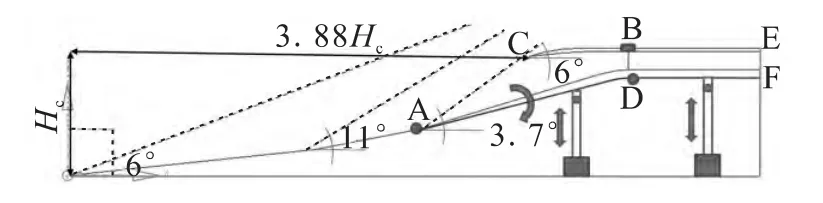
图2 低马赫数段进气道变几何方案示意图Fig.2 Schematic of the variable geometry inlet during low Mach number
此时第三级压缩角降为2.3°,总收缩比降为3.5,内收缩比降为1.41。由于隔离段出口高度的设计要求,此时需要沿D点将喉道后的型面转为水平。
2 数值计算方法
采用Fluent软件进行求解,通量差分采用AUSM格式,湍流模型为Re-Normalization Group(RNG)k-ε模型,流动方程、k方程、ε方程均选择二阶迎风格式离散,近壁采用非平衡壁面函数法。由于模型和流动的对称性,取一半模型进行计算。为了适应粘性计算和捕获激波的需要,加密壁面附近的网格和局部网格,网格量约为10万。采用Sutherland公式计算分子粘性系数,壁面取绝热无滑移和固体边界条件,采用压力远场和压力出口边界条件。各残差指标至少下降3个数量级并且流量沿程守恒时认为数值计算结果收敛。文献 [15]对该数值计算方法进行了试验校验,表明其可以较好模拟高超声速进气道复杂流场结构。
另外,本文主要研究部分顶板转动+唇口平移变几何方案的可行性,因此只开展了二维数值计算,没有考虑三维侧板构型和前挡板等对进气道的影响。按照ΔMa/ΔH=1/2(1/km)的方式给定来流条件,其中来流Ma=6.0时,高度H=24 km。
3 变几何进气道计算结果分析
3.1 Ma=4.0~7.0时进气道流场特点与性能
对基准进气道进行数值计算,图3给出了不同来流马赫数的流场结构。Ma=4.0~6.0时,外压激波依次封口,而且内收缩段流场结构良好,在设计点Ma=6.0时,唇口激波打在肩部之后,造成了很小分离。但是,Ma=7.0时三道外压激波均打到唇口以内,一方面唇口内型面出现一段明显的膨胀加速区,造成唇口激波强度增大;另一方面,三道外压激波汇聚,较强的顶压激波与唇口附面层相互作用,这样不但使唇口处出现大面积的分离,而且强的诱导激波打在顶板肩部后的附面层引起了更大面积的分离,最终导致进气道不起动。
表1给出了基准进气道的总体性能参数:流量系数为φ,总压恢复系数为σ,增压比p/p0以及出口平均马赫数Mae,下标th表示喉道截面,e表示出口截面。可以看出,采用激波依次封口的设计理念,进气道的流量系数很高,Ma=4.0时达到了0.80。整个Ma=4.0~6.0范围内性能较优,设计点时出口总压恢复系数达到了0.571,起动马赫数为3.82。
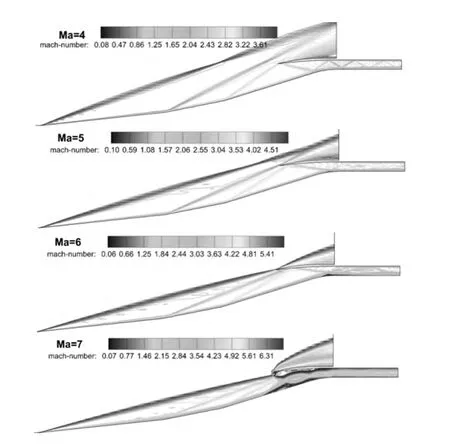
图3 不同来流马赫数时基准进气道的流场Fig.3 Flow field of reference inlet at different incoming Mach numbers

表1 不同来流马赫数时基准进气道的总体性能参数Tab.1 Overall performance parameters of reference inlet at different incoming Mach numbers
分析Ma=7.0时的流场可知,唇口内侧的分离主要是由于激波汇聚且打在发展的附面层之上,因此可以通过向后平移唇口BC(见图2),使外压激波正好位于唇口前缘点C,这样在不降低流量的前提下避免唇口分离并减弱唇口激波强度,进而避免顶板分离。以基准进气道的唇口前缘点C为原点,此时平移距离为△x/Hc=3.37。图4表明此时进气道可以起动,外压激波封口而且肩部的低速区很小,其总体性能良好(见表2)。另外,后移唇口可以达到减小内收缩比,实现更低马赫数自起动的目的。
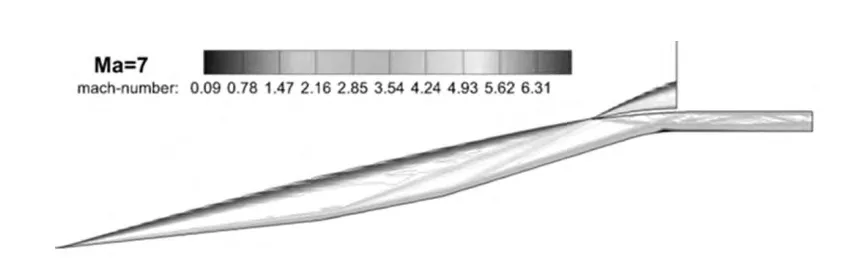
图4 Ma=7.0时平移唇口进气道的流场Fig.4 Flow field of the inlet with translating cowl at Ma=7.0
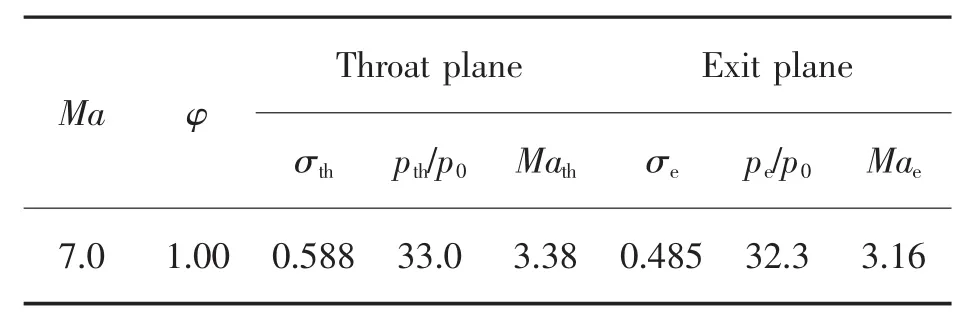
表2 Ma=7.0时平移唇口进气道的总体性能参数Tab.2 Overall performance parameters of the inlet with translating cowl at Ma=7.0
3.2 Ma=2.5~4.0时进气道流场特点与性能
对低马赫数段的进气道构型(见图2)开展二维计算,图5可以看出,Ma=3.0时第三道激波几乎封口,内压段和隔离段内流场结构良好。
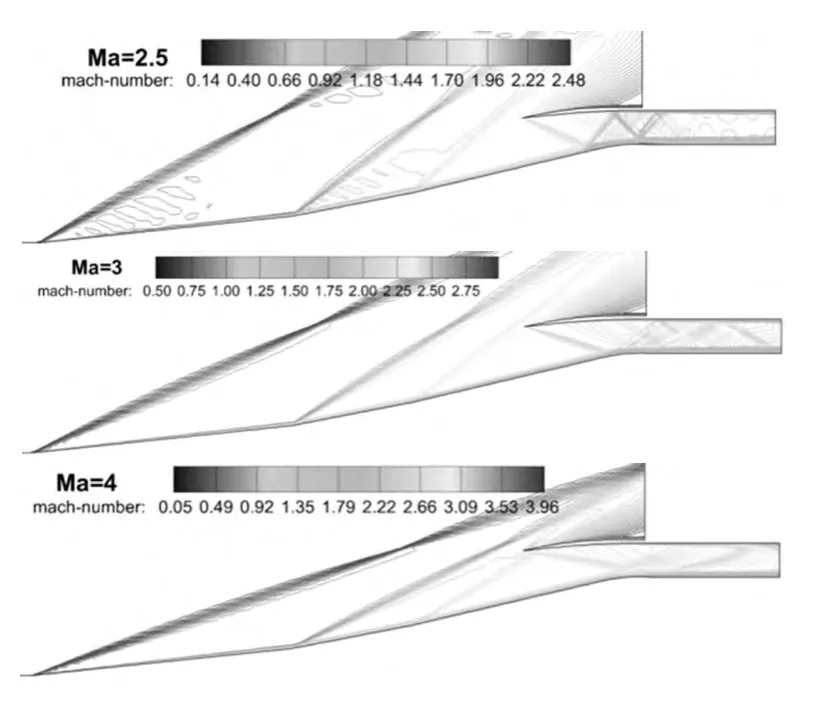
图5 不同来流马赫数时转动部分顶板进气道的流场Fig.5 Flow field of the inlet with rotating partial top wall at different incoming Mach numbers
Ma=2.5时,该进气道可以顺利起动,隔离段内反射波系清晰,从性能参数可以看出(见表3),喉道马赫数达到了1.22,即将进入不起动状态。Ma=4.0时,第三道外压激波打进唇口以内,此时流量系数相对表1不发生变化,但是由于第三级压缩角的减小,使得出口压缩量明显降低,相对降低了66%,但是出口总压恢复系数相对增加了11.4%。此时,唇口激波几乎打在肩部,隔离段内反射激波很弱。

表3 不同来流马赫数时转动部分顶板进气道的总体性能参数Tab.3 Overall performance parameters of the inlet with rotating partial top wall at different incoming Mach numbers
3.3 变几何进气道的自起动性能
为了保证变几何进气道正常工作,必须满足Ma=2.5时自起动,这里只需对Ma=2.5~4.5的构型进行研究。按照准定常过程计算自起动马赫数,即首先计算获得一个低马赫数下的不起动流场,然后不断增加来流马赫数直至进气道起动,该马赫数即为自起动马赫数。数值计算表明,低马赫数段构型在Ma=2.0时无法起动,唇口前存在一道正激波,而且形成的分离包产生的诱导激波与正激波相交,形成“λ”波,见图6。
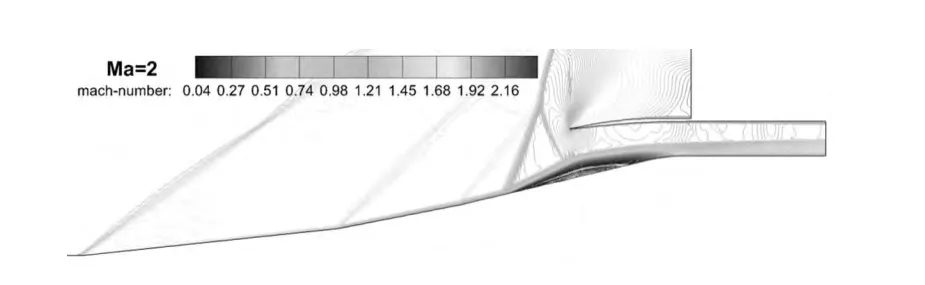
图6 Ma=2.0时转动部分顶板进气道的不起动流场Fig.6 Unstart flow field of the inlet with rotating partial top wall at Ma=2.0
在该不起动流场基础上,不断增加来流马赫数进行计算(ΔMa=0.1),即使在Ma=2.8时也无法自起动。这主要是因为此时内收缩比过大(Rci=1.41),按照Kantrowitz限制,其唇口平均马赫数至少大于3.0。
为了解决自起动问题,将唇口向后平移来减小内收缩比。为了尽可能地减少调节位置,唇口向后平移位置与Ma=7.0时相同(△x/Hc=3.37),此时内收缩比降为1.16。Ma=2.0时流场有所改善,但是正激波贴口,分离包仍然存在。在此不起动流场上继续增加来流马赫数,Ma=2.3时正激波被吞入,流场正常建立,进气道自起动,见图7,表4给出了此时的性能参数。进气道自起动后,立即将唇口向前平移复位,可以提高总体性能和流量系数。

图7 Ma=2.3时部分顶板转动+唇口平移进气道的自起动流场Fig.7 Self-start flow field of inlet with rotating partial top wall and translating cowl at Ma=2.0
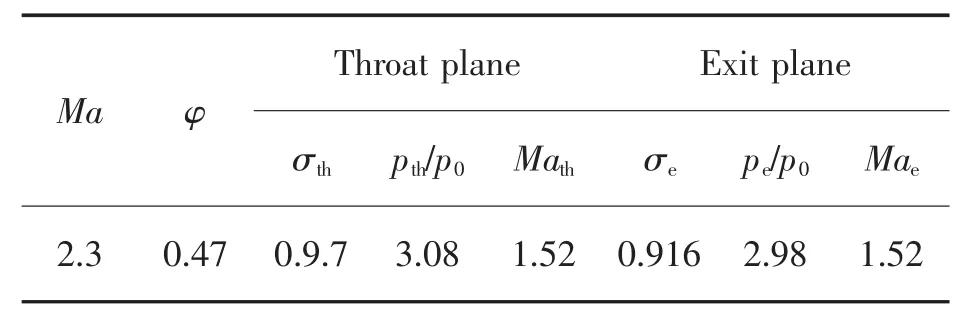
表4 Ma=2.3时部分顶板转动+唇口平移进气道的总体性能参数Tab.4 Overall performance parameters of inlet with rotating partial top wall and translating cowl at Ma=2.3
4 变几何进气道的调节方法
综上研究可知,按照RBCC发动机工作模态在Ma=2.5~7.0范围内工作时,变几何进气道的调节过程如下:
1)当2.5≤Ma≤4.0时,进气道保持图8的构型,此时相对基准进气道构型(虚线),顶板沿着第三级转折点(A点)顺时针转动3.7°,同时绕D点旋转使扩压段保持水平。此时若出现不起动,可以将唇口BC向后平移△x/Hc=3.37,自起动后唇口立即复位。
2)当4.0≤Ma≤6.0时,进气道保持基本构型,即在图8构型基础上,将顶板沿A点逆时针转动3.7°,见图9。
3)当6.0≤Ma≤7.0时,在基准构型的基础上,仅向后平移唇口△x/Hc=3.37,见图10。

图8 2.5≤Ma≤4.0时变几何进气道的构型Fig.8 Configuration of variable geometry inlet with at Mach number 2.5~4.0
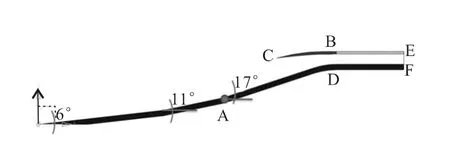
图9 4.0≤Ma≤6.0时变几何进气道的构型(基准构型)Fig.9 Configuration of variable geometry inlet at Mach number 4.0~6.0(reference configuration)

图10 6.0≤Ma≤7.0时变几何进气道的构型Fig.10 Configuration of variable geometry inlet at Mach number 6.0~7.0
5 结论
1)采用激波依次封口设计概念的变几何进气道具有良好的流量捕获能力,Ma=2.5时流量系数高达0.59,这对飞行器加速十分有利。
2)转动部分顶板的简单变几何方案解决了宽马赫数范围内进气道高效压缩和低马赫数起动问题,整个工作范围内总体性能较优。
3)向后平移唇口至同一位置,不但可以使基准构型在超额定工况Ma=7.0时起动,而且可以使低马赫数段构型Ma=2.3时自起动。
4)按照最终确定的调节方法,变几何进气道可在宽马赫数范围内高效工作,工程应用可行。
[1]FOSTER R W,ESCHER WJ D,ROBINSON J W.Studies of an extensively axisymmetric rocket based combined cycle(RBCC)engine powered single-stage-to-orbit(SSTO)vehicle,AIAA 1989-2294[R].USA:AIAA,1989.
[2]CZYSZ P A,LITTLE M J.Rocket based combined cycle engine(RBCC):a propulsion system for the 21st century,AIAA1993-5096[R].USA:AIAA,1993.
[3]EHRLICH C F.Early studies of RBCC applications and lessonslearnedfortoday,AIAA2000-3105[R].USA:AIAA,2000.
[4]吕翔.RBCC推进系统总体设计方法研究[D].西安:西北工业大学,2008.
[5]张蒙正,李斌,王君,等.关于RBCC动力系统的思考[J].火箭推进,2013,39(1):1-7.ZHANG Meng zheng,LI Bin,WANG Jun,et al.Thinking about RBCC propulsion system[J].Journal of Rocket Propulsion,2013,39(1):1-7.
[6]KODERA M,OGAWA H,TOMIOKA S,et al.Multiobjective design and trajectory optimization of space transport systems with RBCC propulsion via evolutionary algorithms and pseudo spectral methods,AIAA 2014-0629[R].USA:AIAA,2014.
[7]张蒙正,张玫,严俊峰,等.RBCC动力系统工作模态问题[J].火箭推进,2015,41(2):1-6.ZHANG Meng zheng,ZHANG Mei,YAN Jun feng,et al.Discussion about work modality of RBCC power system[J].Journal of Rocket Propulsion,2015,41(2):1-6.
[8]金志光,张堃元,刘媛.马赫数4~7的高超侧压式进气道气动设计与性能 [J].航空动力学报,2011,26(6):1201-1208.
[9]COCKRELL C E,AUSLENDER A H,WHITE J A,et al.Aeroheating predictions for the X-43 cowl-closed configuration at Mach 7 and 10,AIAA 2002-0218[R].USA:AIAA,2002.
[10]FALEMPIN F,SERRE L.French flight testing program LEA status in 2009,AIAA 2009-7227[R].USA:AIAA,2009.
[11]TREFNY C J,ROCHE J M.Performance validation approach for the gtx air-breathing launch vehicle,NASA/TM 2002-211495[R].USA:NASA,2002.
[12]BULMAN M,SIEBENHAAR A.The strutjet engine:exploding the myths surrounding high speed airbreathing propulsion,AIAA 1995-2475[R].USA:AIAA,1995.
[13]KANDA T,TOMIOKA S,UEDA S,et al.Design of sub-scale rocket-ramjet combined cycle engine model,IAC-05-C4.5.03[R].[S.l.]:IAC,2005.
[14]张浩,李光熙,李江,等.内置中心支板的RBCC变几何二元进气道设计与数值模拟 [J].固体火箭技术,2014,37(2):184-191.
[15]王翼.高超声速进气道启动问题研究[D].长沙:国防科学技术大学,2008.

