中心射流泵多参数优化设计

李春乐，李永鹏，陈 炜，李向阳

（西安航天动力研究所，陕西西安710100）

0 引言

因无运动部件且结构简单，射流泵被广泛应用于各个行业中[1]。影响射流泵性能的结构参数较多，但国内大多数仅分析射流泵中一、二个参数与性能的关系[2]，而性能随参数变化规律是随着其它参数变化而变化的[3]，只分析一、二个参数已无法满足越来越精细化的设计。

本文通过多参数优化设计对中心射流泵进行研究，以效率最大为优化目标，提出了中心射流泵的一种优化设计方法，可以同时分析多个参数对泵性能的影响，得到最优结构。

1 中心射流泵简介

中心射流泵基本结构如图1所示，主要由三部分组成：喷嘴、喉管和扩散管。其工作原理是将工作流体通过喷嘴高速喷出，同时静压能部分转换为动能。管内形成低压，液体被吸入管内。两股液体在喉管中进行混合和能量交换，工作液体速度减小，被吸液体速度增大，在喉管出口处速度趋于一致。混合液体通过扩散管时，随着流道的增大，速度逐渐降低，动能转化为压力能，混合液体压力随之升高。

能量交换主要发生在喷嘴出口至喉管末端[4]，这一段结构对中心射流泵性能影响最大，主要由4个结构参数组成：

1)面积比m-喉管面积与喷嘴出口面积之比，d22/d12；

2)喉嘴距系数A1-喉嘴距与喷嘴直径之比，L1/d1；

3)喉管长径比A2-喉管长度与喉管直径之比，L2/d2；

4)渐缩段角度α。

图1 中心射流泵示意图Fig.1 Schematic diagram of center jet pump

以上述4个参数为变量，效率最高为优化目标，对中心射流泵进行多参数优化设计，本文所研究的中心射流泵工作流体压力较高，工作流体与被吸流体压力比不小于10。

2 多参数优化分析

以三参数（a，b，c）优化为例，如图2所示，传统优化方只能在2个参数（b，c）固定的情况下，找到最佳的参数a，而b和c改变后，必须重新找到此时的最佳参数a。这种方法很难找到最优的参数组合，如需优化更多的参数，则传统方法将很难实现。

图2 传统优化方法Fig.2 Traditional optimization method

如图3所示，多参数优化设计同时改变a，b和c这3个参数，参数的组合形式来源于统计学理论，如部分因子法，田口法，拉丁超立方法等，根据这些统计学方法（试验设计方法），可以在较少的参数组合下，找到最优参数组合。同时，根据每组参数的计算结果，还可以列出参数与优化目标之间的函数关系（响应面模型），计算出最优的参数组合。变量数越多，所需的计算次数也越多，但都可以得到最优解。

图3 多参数优化方法Fig.3 Multi-parameter optimization method

图4 本文多参数优化设计流程Fig.4 Flowchart of multi-parameter optimization design

为了得到更准确的优化结果，需要对掺混段的4个参数同时进行优化分析，只能采用多参数优化分析方法才能实现。

本文的多参数优化设计是在参数化建模的基础上，选取合适的试验设计方法，将设计参数排列组合，对每一种组合进行数值计算，根据计算结果以及优化目标确定最优的设计参数，具体流程如图4所示。

2.1 试验设计

主要设计参数选择完之后就是将这些设计参数在一定的变化范围内进行组合排列，得到这些排列下相应的性能参数。试验设计就是通过合理的选择样本点来得到相应的性能参数，然后根据这些输入、输出关系进行相关性分析、建立响应面模型。试验设计有两个目的：

1）得出输入参数和输出参数之间的相关性关系，通过相关性的大小分析输入参数对输出参数的影响。一般相关性大，输入参数对输出参数的影响也大，从而找出主要设计参数与次要设计参数。

2）利用试验设计结果，可以建立响应面模型（输入参数与输出参数间的函数关系式），分析输入参数与输出参数的关系，也可以在后续优化中替代仿真程序，根据输入参数，通过函数关系式求解输出参数。

本文试验设计方法选用拉丁超立方法。拉丁超立方法是一种多维分层抽样方法，在优化设计[5]和可靠性计算[6]方面都有较多应用。输入输出之间的关系采用最小二乘法对样本点数据进行泰勒多项式拟合[7]，得出四个设计参数与性能之间的函数关系式。

2.2 优化方法

优化设计问题一般由变量、优化目标、优化函数、约束条件表征。其中，变量代表可改变的设计参数，约束条件把设计参数限制在一定范围内，优化函数表示变量与优化目标之间的关系。

优化方法分为两种，一种是基于导数的优化方法，一种是遗传算法。基于导数的优化方法一般只找到局部最优解，找到的最优解与起始点关系很大，但收敛速度快；遗传算法一般能找到全局最优解，但收敛速度慢，计算量大。本文采用自适应进化算法，是遗传算法的一种，精度和可靠性都很高，且约束条件较光滑时有较大优势。

3 数值计算

射流泵内部流体流动属于高雷诺数强剪切湍射流，由于湍射流流至具有一定的速度和压力的流场内，使整个流动不具有相似的性质，所以长期以来，对于射流泵内部流动机理认识不充分[8]。近几年来，随着试验测量手段的发展和CFD软件的出现，可以通过试验和数值模拟两种手段研究射流泵内的流场，从而揭示其内部流动规律。数值计算的准确是最终优化结果可信的前提，本文数值计算的控制方程为三维雷诺平均N-S方程，湍流模型采用标准k-ε模型，近壁区采用标准壁面函数法。

对优化前的产品进行数值计算，计算结果与试验数据对比结果如图5所示。

图5 数值计算结果与试验对比Fig.5 Comparison of numerical results and test

可以看出，中心射流泵数值计算结果与试验数据吻合较好，总体趋势正确。其中，h=H2/H1，q=q2-q1，H1为工作流体入口总压与被吸流体入口总压之差，H2为射流泵出口总压与被吸流体入口总压之差。q1和q2为工作流体和被吸流体体积流量，η为射流泵效率。

对比试验数据结果，证明了数值计算结果可信，每一组参数的计算都采用相同的网格密度以及数值计算方法，确保后续计算结果同样可信。

4 优化结果及分析

基于拉丁超立方法，进行了120次数值计算，根据计算结果，用最小二乘法建立响应面模型，图6为计算结果散点图，图中点离对角线越近，说明响应面模型精度越高。从图中可以看出，所建立的响应面模型与计算结果偏差很小，质量较好，可以根据建立的响应面模型开展后续优化分析工作。

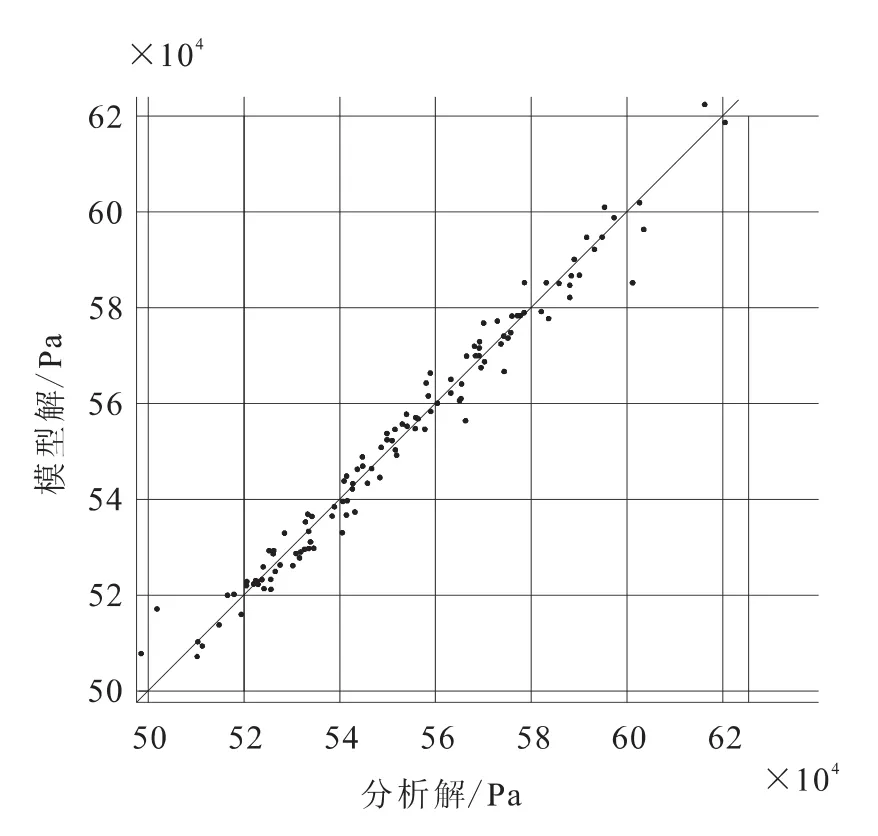
图6 计算结果散点图Fig.6 Scatter diagram of calculated results

表1列出了中心射流泵参数与性能的相关性，可以看出，面积比与射流泵性能的相关性较大，相关系数为-0.85；喉管长径比与性能也有一定的相关性，相关系数为0.19，喉嘴距系数以及渐缩段角度与性能相关性较小，相关系数分别为-0.11以及0.07。通过以上4个参数与性能的相关性分析得出，面积比是主要设计参数。

表1 中心射流泵参数与性能相关性Tab.1 Correlation between parameters and performance of center jet pump

以效率最高为优化目标，得到的最优设计参数如表2所示。因面积比受限结构等因素，优化下限为30。优化前后的数值计算结果如图7所示，优化前在设计点效率为10.35%，经过多参优化后效率为11.71%，提高了1.36%。

表2 中心射流泵最优参数Tab.2 Optimal parameters of center jet pump

图7 优化前后效率曲线对比Fig.7 Comparison of efficiency curves before and after optimization

对优化前后泵流场进行了对比分析，优化前后流场如图8和图9所示。

图8 优化前流线图Fig.8 Streamline diagram before optimization

图9 优化后流线图Fig.9 Streamline diagram after optimization

从图中可以看出，相比优化后，优化前喉管中的漩涡体积较大。漩涡会带来能量损失，使泵效率降低。

5 结论

采用多参数优化方法，对中心射流泵4个设计参数与性能之间的关系进行了分析，以效率最高为目标，得到了最优的设计参数，优化结果对工程设计有一定指导意义。与传统优化方法相比，多参数优化考虑了参数之间的相互影响关系，优化结果更全面、准确，是中心射流泵设计的一种新方法。

[1]WINOTOSH,LIH,SHAH D A.Efficiency of jet pumps[J].Journal ofHydraulic Engineering,2000,126(2)：150-56.

[2]龙新平,朱劲木,梁爱国,刘景植.射流泵喉管最优长度的数值计算[J].水利学报,2003(10)：14-18.

[3]王常斌,林建忠,石兴.射流泵最佳参数的确定方法[J].流体机械,2004,32(9)：21-25.

[4]陆宏圻.喷射技术理论及应用[M].武汉：武汉大学出版社,2004.

[5]陈沛,韩旭,姜潮,张正.基于最小二乘映射的多参数结构问题快速计算方法[J].中国机械工程,2011,22(6)：706-709.

[6]刘纪涛,刘飞,张为华.基于拉丁超立方抽样及响应面的结构模糊分析[J].机械强度,2011,33(1)：73-76.

[7]李庆杨,王能超,易大义.数值分析[M].北京：清华大学出版社,2008.

[8]LEE Jun-Hee,KIM H D.Studies on flow characteristics of variable ejectorsystems,AIAA2006-4884[R].USA：AIAA,2006.