基于分数阶PID的高频除尘电源控制方法研究

仇家胜，章飞，曾庆军

(江苏科技大学 电子信息学院，江苏 镇江 212000)

0 引言

目前国内广泛采用的静电除尘电源主要是工频电源，这类电源存在输出电压脉动大，输出平均电压低，除尘效率相对较低等缺点。高频除尘电源采用全控型器件，系统响应速度快，在电场发生闪络或短路时能够进行快速调整，并且输出电压纹波小，平均电压高，不仅能够提高电源工作效率，增大功率因数，而且还可以提高除尘效率，实现减排。因此，高频静电除尘电源必然能够替代原工频除尘电源成为静电除尘电源的新选择［1］。

现有的高频除尘电源控制方法大多采用简单闭环控制方法或采用整数阶PID方法，简单闭环控制方法控制方式简单但是控制效果较差，传统PID控制方法对整数阶对象控制效果显著，而高频除尘电源中的逆变环节为分数阶控制对象，传统PID控制方法控制效果不够理想［2-3］。分数阶PID控制方法与整数阶PID控制方法相比，具有上升时间快，稳定时间短，鲁棒性强的优点;另外，分数阶PID控制方法的控制对象范围更为广泛，尤其对分数阶控制对象控制效果更为显著，因此，本文提出一种高频除尘电源的分数阶PID控制方法，给出了分数阶微积分的Oustaloup滤波器近似算法，并在MATLAB中实现了该Oustaloup滤波器近似算法，最后，利用Simulink搭建并仿真了基于分数阶PID控制方法的高频除尘电源控制系统，同时将分数阶PID控制方法应用于一台72 kW的高频除尘电源系统中，结果表明高频除尘电源系统的分数阶PID控制方法与整数阶PID控制方法相比具有更好的动态特性。

1 分数阶PID定义

分数阶微积分定义方式主要有Grünwald-Letnikov(GL)分数阶微积分定义［4］，Riemann-Liouvile(RL)分数阶微积分定义，Caputo分数阶微积分定义，其中被广泛应用的是RL分数阶微积分定义［5］，RL 的定义为:

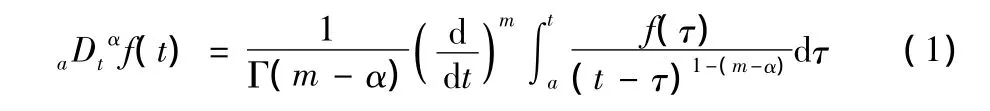
式中m-1＜α＜m，Γ(·)是Euler Gamma函数。其中a是微积分基本操作算子［6］，α，t是基本操作算子的上下限，α是微积分的阶次是一个复数，本文假定为实数，显然当α＞0时a为微分算子，α ＜0时，a为积分算子。

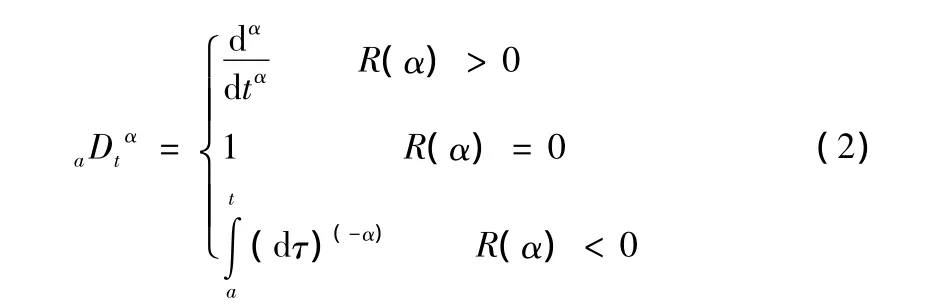
分数阶PID控制器一般记为PIλDμ形式［7］，其中λ和μ是积分和微分的阶次并且为正实数，其传递函数为:

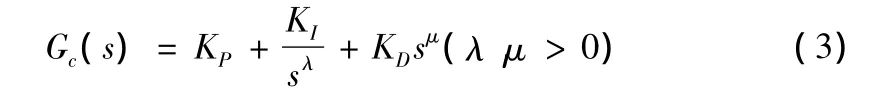
同理，时域中的表达式如下:

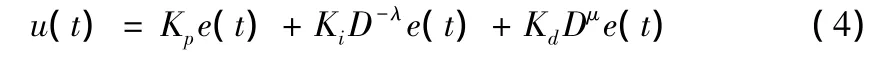
由传递函数可知，传统的整数阶PID控制器是分数阶PID控制器的一中特例，当λ=1，μ=1时，分数阶PID控制器就变成了整数阶PID控制器，由此可见，分数阶PID控制器比整数阶PID控制器的控制对象更为广泛［8］。

2 基于分数阶PID的逆变控制方法

基于分数阶PID的高频除尘电源控制系统结构如图1所示，整个除尘电源系统由四部分组成:三相桥式整流，全桥逆变，高频变压，高压硅堆整流。该系统输入为380 V三相交流电源，先经过三相滤波器进行滤波，然后进入三相桥式整流进行整流，由电容滤波之后进入逆变电路，逆变之后由高频变压器进行升压，进而由高压硅堆整流输出至本体。其中关于逆变电路部分，考虑到硬开关型逆变电路有较大的开关损耗以及造成大量的电磁干扰等问题，逆变电路采用LCC谐振型逆变电路［9］，谐振型逆变电路可以很好的改善硬开关型逆变电路的诸多缺点［10］，高频除尘电源的分数阶PID控制方法主要是对IGBT进行变频逆变控制，进而对高频逆变电路的LCC谐振过程进行控制。

高频除尘电源的分数阶PID控制方法的基本原理是通过将高频除尘电源的输出电压和设定值比较，得到的电压差值反馈至分数阶PID控制环节，根据分数阶PID的时域表达式，即式(4)计算得到分数阶PID的误差输出值为［11］:

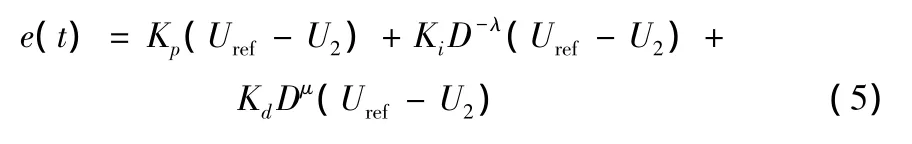
然后，再将该误差值转换为IGBT的驱动频率，结合谐振电路的参数设置，可以得出驱动频率范围为0～30 kHz的方波，固定占空比为50%，具体频率调制波形(PFM)由PFM模块完成。

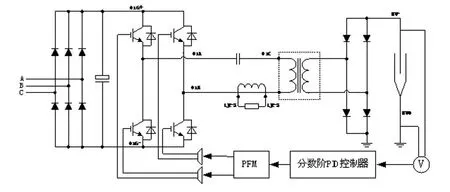
图1 基于分数阶PID的高频除尘电源控制系统结构

高频除尘电源分数阶PID控制方法中，对于分数阶微积分的近似计算是算法实现的核心，由于高频除尘电源系统结构复杂，很难建立精确的数学模型并求解出传递函数，因此常采用滤波器近似算法实现对分数阶微积分的近似计算［12］，而在众多近似算法中，Oustaloup滤波器算法性能最为出众，所以本文采用Oustaloup滤波器算法来实现高频除尘电源分数阶PID控制方法中的分数阶微积分的近似计算。

3 Oustaloup滤波器算法实现

由于纯微分器的频域特性是斜线，任何滤波器都不能在全频段进行近似计算［13］，所以只能在特定的频段范围内进行近似计算，假设需要近似的频段为(ωb，ωh)，则可以将相应的滤波器写成:

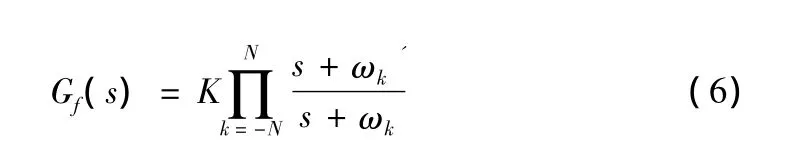
其中:

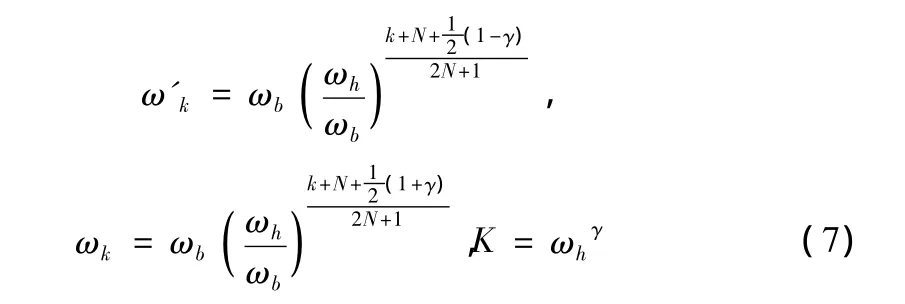
根据上述算法原理，通过建立MATLAB函数oustafod()来构造Oustaloup滤波器，假设输入信号为y(t)，则经过滤波器输出的分数阶微积分信号近似为aDtαy(t)。具体MATLAB函数oustafod()程序如下:

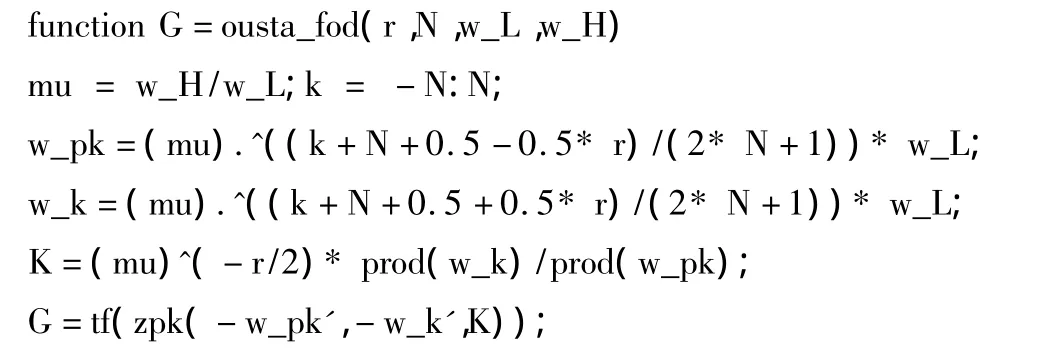
其中r是微积分的阶次，r＞0表示微分近似，r＜0表示积分近似;变量2N+1为滤波器的阶次;(w_L，w_H)是选定的特定频段，一般取w_L*w_H=1。

4 高频除尘电源分数阶PID控制方法仿真及实验

由于高频除尘电源控制系统较为复杂，很难建立精确的数学模型，因此本文采用MATLAB的Simulink搭建了基于分数阶PID控制方法的高频除尘电源控制系统。对于分数阶PID控制方法中的λ和μ的取值区间通常限定在(0.01，1.00)之间，取值步长为0.01，仿真系统输出电压设定值为-70 kV，依据ITAE准则，计算误差与时间乘积和最小的一组数据，即通过λ和μ的不同取值根据式(8)计算J的值，其中式(8)中的e(t)见式(5)所示，t为仿真时间:

选取ITAE值最小的一组参数，经过仿真最终确定:λ=0.1，μ=0.05，得到分数阶PID控制器为:

基于分数阶PID控制方法的高频除尘电源的电路仿真图如图2所示。

图3是高频除尘电源的分数阶PID控制方法和整数阶PID控制方法的控制效果对比图，其中仿真系统输出电压设定值为-70 kV，从图中可知，两种控制方法的上升速度几乎一致，但是整数阶PID控制方法的超调量比分数阶PID控制方法的超调量大，尤其在稳定时间方面，分数阶PID控制方法明显优于整数阶PID控制方法。

图3中嵌套图形表示的是基于两种控制方法的高频除尘电源系统稳定输出局部放大图，从图中可以看出整数阶PID控制方法的稳态误差点与设定值相差大，稳态误差点的分布也相对较为分散;相比之下，分数阶PID控制方法的稳态误差点分布较为集中并且与设定值相差不大。根据图3得到表1。从表中可以看出，分数阶PID控制方法的稳定时间是0.8 ms，而整数阶PID控制方法的稳定时间则为3 ms，是分数阶PID控制方法稳定时间的4倍左右;整数阶PID的超调量是4 kV，与分数阶PID控制方法相差2 kV;但是在稳态误差和均方误差方面，分数阶PID控制方法的稳态误差均值只有91 V，均方误差为138 V，而整数阶PID控制方法的稳态误差均值和均方误差值是其5倍左右;综上所述，高频除尘电源分数阶PID控制方法在系统稳定时间，超调量以及稳态误差方面全面优于整数阶PID控制方法，其控制效果更为理想。

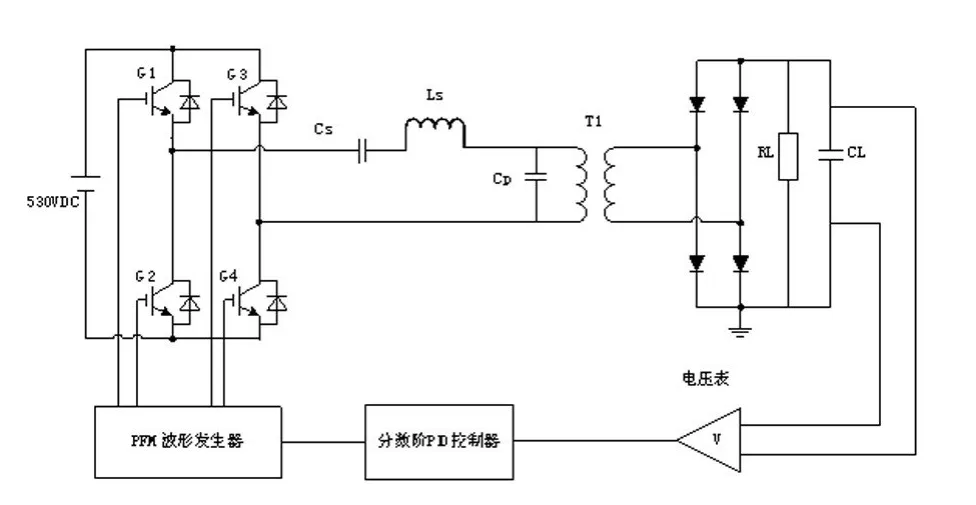
图2 高频除尘电源的分数阶PID控制方法仿真电路

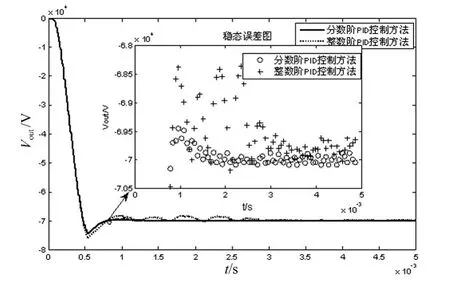
图3 控制效果对比

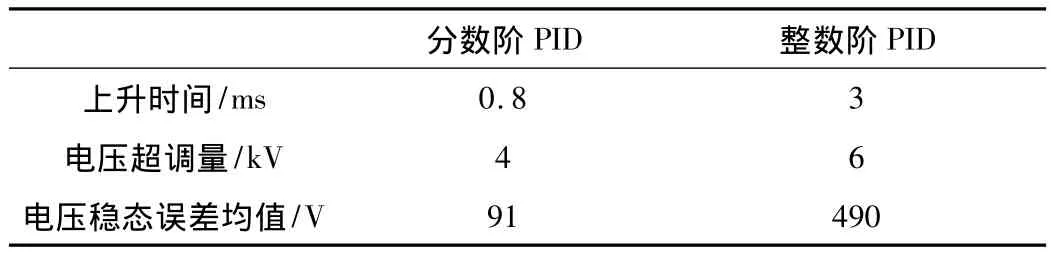
表1 数据对比

将本文所提分数阶PID控制方法应用于72 kW高频除尘电源系统，该电源系统以TMS320F2812为核心处理器，采用英飞凌FZ400R12KE4型IGBT，输入电源为工频380 V，LCC串联谐振电容为 1 μF，高频变压器变比为 1∶140，漏感为 15 μH，寄生电容为0.8 μF，图4和图5给出了基于分数阶PID的高频除尘电源实际测量的谐振电流波形和输出电压波形。

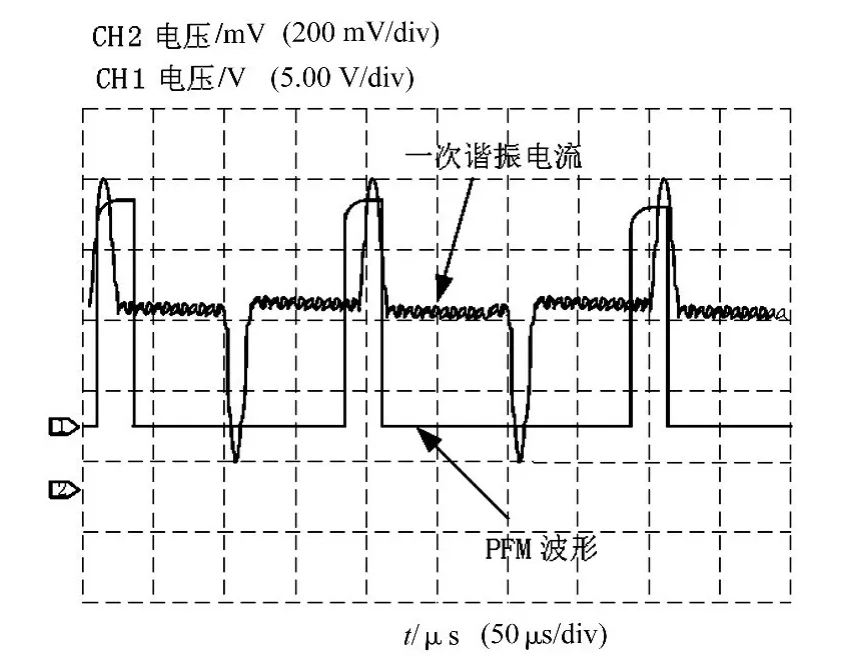
图4 电流断续模式波形

图5 输出电压电流波形

从图4中可以看出，LCC逆变电路工作在电流断续模式下，其电流波形与PWM波形符合理论分析，由于采用纯阻性模拟负载，因此电流输出波形和电压输出波形如图5所示，从图5中可以看出电流波形和电压波形均没有直流分量并且变化趋势完全相同，此时输出电压的最大值达到82 kV。通过实验结果表明，分数阶PID控制方法比整数阶PID控制方法具有更好的动态特性。

5 结束语

本文提出一种高频除尘电源的分数阶PID控制方法，通过与整数阶PID控制方法相比较，进一步验证了分数阶PID控制方法在高频除尘电源系统中的优越性。利用Simulink搭建并仿真了基于分数阶PID的高频除尘电源的系统结构，并通过实验数据表明分数阶PID控制方法在系统稳定时间，超调量以及稳态误差和均方误差方面全面优于整数阶PID控制方法。本文采用ITAE准则实现对高频除尘电源分数阶PID控制方法的参数整定，该方法运行效率较低，对于其他执行效率高的参数整定方法有待进一步研究。

［1］吴伟.高频静电除尘电源监控系统设计［D］.秦皇岛:燕山大学，2013.

［2］薛定宇，赵春娜.分数阶系统的分数阶PID控制器设计［J］.控制理论及应用，2007，24(5):771-776.

［3］王璇，张小凤，周丰，等.三相电压型PWM整流器分数阶PID直接功率控制［J］.电气传动.2013，43(4):45-49.

［4］秦昌茂.高超声速飞行器分数阶PID及自抗扰控制研究［D］.哈尔滨:哈尔滨工业大学，2011.

［5］薛定宇，陈阳泉.高等应用数学问题的MATLAB求解［M］.北京:清华大学出版社，2004.

［6］薛定宇，陈阳泉.控制数学问题的MATLAB求解［M］.北京:清华大学出版社，2007.

［7］I PODLUBNY.Fractional-order systems and PID-controllers［J］.IEEE Transactions on Automatic Control，1994，44(1):208-214.

［8］K A TEHRANI，A AMIRAHMADI，S M R RAFIEI，et al.Design of fractional order PID controller for boost converter based on multiobjective optimization［C］//14th International Power Electronics and Motion Control Conference，EPE-PEMC，Ohrid，Macedonia，September 6-8，2010:179-185.

［9］夏冰.LCC谐振变换器在大功率高输出电压场合的应用研究［D］.南京:南京航空航天大学，2008.

［10］常磊，刘军，何湘宁.C-filter LCC断续工作模式逆变桥损耗分析［J］.电力电子技术.2013，47(2):1-3.

［11］L MANYU，D HUAYING，L GUISHU.SVC voltage regulator based on fractional order PID［C］//2012 International Conference on Control Engineering and Communication Technology， Shenyang， Liaoning，China，December 7-9，2012:28-32.

［12］B M VINAGRE， I PODLUBNY， A HERNANDEZ， et al. Some approximations of fractional order operators used in control therory and applications［J］.Fractional Calculus and Applied Analysis，2000，3(3):231-248.

［13］A OUSTALOUP，F LEVRON，B MATHIEU，et al.Frequency-band complex noninteger differentiator:characterization and synthesis［J］.IEEE Transactions on Circuit and Systems-I:Fundamental Theory and Applications，2000，47(1):25-39.