BP神经网络在气动人工肌肉拉力预测中的应用

顾宝彤，刘　凯，马　韬

（南京航空航天大学机电学院，江苏 南京 210016）

BP神经网络在气动人工肌肉拉力预测中的应用

顾宝彤，刘凯，马韬

（南京航空航天大学机电学院，江苏 南京 210016）

在气动人工肌肉的静态建模中，为寻找拉力与气压和位移的函数关系，该文利用训练后的BP神经网络预测气动人工肌肉输出力。将准静态实验获得的气压、位移和对应的输出拉力代入BP神经网络进行训练，得到气动人工肌肉的BP神经网络静态模型。预测结果表明，预测拉力与试验测得拉力相关系数达0.99以上，且通过BP神经网络预测拉力与实测拉力误差率在较大收缩范围内维持在较低水平，从而证明根据BP神经网络预测拉力的静态模型是可行的。

气动肌肉；驱动器；BP神经网络；输出力；预测

0　引　言

气动人工肌肉驱动器主要由纤维包裹的橡胶制成，并且两端通过端盖相连。橡胶管具有良好的弹性而纤维刚度很大，所以当橡胶管加压时，气动人工肌肉在轴向缩短、径向扩大，与此同时产生拉力。与电动和液压执行机构相比，气动人工肌肉响应迅速，并且功率/重量比和功率/体积比很高，但人工肌肉的非线性导致对其自身控制相对困难，所以建立人工肌肉模型意义重大。

气动人工肌肉模型主要研究方向是静态模型和动态模型。静态模型是将气动人工肌肉收缩和拉伸过程看成一个准静态过程，主要应用在动态响应要求不高的场合；动态模型主要关注人工肌肉动态响应特性，如在阶跃气压激励下，肌肉收缩长度与时间关系。

气动人工肌肉静态建模主要从能量守恒、力平衡及直接拟合角度考虑。Chou[1]从能量守恒角度，根据虚功原理建立气动人工肌肉输入压力、位移和输出拉力之间的理论关系。力平衡模型是由Ferraresi等[2]在2001年提出，后来研究者通过引入非圆柱形状和变厚度等参数改进了该模型。直接拟合根据实验台测量输入拉力、气压和输出拉力后寻找合适数据模型拟合数据，于海涛等[3]通过改进的Tondu-Lopez模型拟合了三者关系。

人工神经网络[4]可实现多个输入因素与输出目标的非线性映射关系，能够灵活方便地对多个因素、复杂的未知变量进行建模。神经网络主要用在人工肌肉动态模型，田社平等[4]提出的局域神经网络人工肌肉非线性控制方法，能够获得更快控制速度和更高的精度；沈伟等[5]针对气动人工肌肉设计了自适应模糊小脑模型神经网络控制器以实现更好的跟踪和控制性能；高建英等[6]利用BP神经网络对单根气动人工肌肉阶跃响应的动态响应进行研究；王冬青等[7]利用递归神经网络对人工肌肉手臂进行非线性动态建模。

由于上文提到的静态建模结果往往和实际测量值有较大偏差，BP神经网络结构简单且学习算法相对比较成熟，所以本文引入BP神经网络参与静态建模，利用神经网络自学习能力提高静态建模准确度。

1　气动人工肌肉模型特性测试

人工肌肉测试系统主要包括气动人工肌肉、气压比例伺服阀、气压传感器、力传感器、数据采集模块、运动控制模块和测控软件等。气动人工肌肉（FESTO公司提供，型号DMSP-10-100N-RM-CM）的初始长度100mm，最大收缩率为25%。气动人工肌肉一端连接到力传感器，另一端固定在滑动平台上并通过手轮驱动。气源通过伺服阀（SMC公司，型号ITV1050-312-l2）和气压传感器（SMC公司，型号PSE530）输送到人工肌肉。人工肌肉通过电位器（GRFRAN公司，型号PK-M-400）检测位移。使用数据采集卡（阿尔泰科技公司，型号PCI8735）采集力、位移和压力，采样频率为50Hz；使用运动控制卡（型号PCI8301）控制伺服阀。通过C/C++编写测控软件实时采集传感器数据和控制输出气压。

为了分析气动人工肌肉输入气压、轴向输出力及收缩率3者静态关系，需要测量人工肌肉在输入气压下的等压特性曲线。实验流程如图1所示，在特定的输入气压下，调节手轮使得人工肌肉缓慢收缩到输出力＜0N，在此过程中每收缩1mm记录传感器数据，接着反方向调节手轮使得人工肌肉缓慢拉伸至初始长度，在此过程中每拉伸1mm记录传感器数据。

图1　试验流程

以人工肌肉为研究对象，在100～800 kPa每隔100 kPa重复进行3次收缩和拉伸测试，每个记录点的拉力取平均值，获得每个气压下的拉力与收缩率（收缩量/初始长度）关系如图2所示。图中每个气压的上方曲线为拉伸过程中产生输出力，下方曲线为收缩过程中产生输出力。

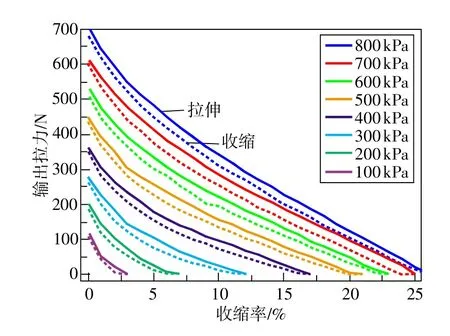
图2　等压测试曲线

2　BP神经网络预测气动肌肉输出力

2.1BP神经网络结构设计

BP神经网络由输入层、隐含层和输出层组成，层与层之间采用全部连接方式，同一层单元之间不存在相互连接。信息从输入层依次向上传递，直达输出层。BP网络算法是通过网络输出误差的反向传播，不断调整和修改网络的连接权值，使网络误差达到最小，从而使该网络实现给定样本数据的输入与输出映射关系。

假设BP神经网络的第Q层为输出层，第q层神经元个数为nq，从第q-1层第j个结点输入到第q层的第i个神经元的连接权值为ωij（q），如图3所示，则从第q-1层到第q层第i个结点变换关系可表示为

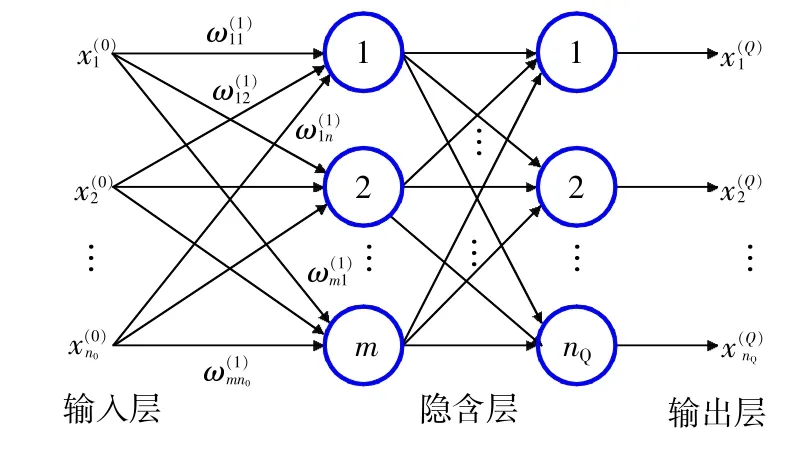
图3　BP神经网络结构示意图

式中i=1～nq，j=1～nq-1，q=1～Q。

复杂网络误差曲面是多维空间曲面，传统的BP算法在训练过程中容易陷入局部最小，为得到合理的神经网络模型，本文采用L-M优化算法[8]，可以使误差函数沿着梯度增大方向继续迭代，从而避免局部最小问题，其连接权值调整公式为

式中ωk和ωk+1分别表示第k和k+1次迭代过程中连接权值组成的向量，Δω为权值增量，它表示为

式中：E——输出层各结点的误差组成的误差向量；

J——该误差向量对连接权值微分的雅可比矩阵；

I——单位矩阵；

μ——试探性的参数，其取值及优化可由计算机辅助完成。

气动人工肌肉建立的静态模型中，因变量为拉力，自变量为位移与输入气压，因此可确定BP神经网络的输入层为2维向量，输出层为单个神经元。经过反复计算，最终确定隐层数取2，第1隐含层的节点数为5，第2隐含层的结点数为10。

神经网络的学习主要通过对样本的反复训练来实现，训练网络的目的在于让系统找出输入与输出之间的本质联系[9]。为了消除噪声数据的影响，同时得到满意的输入输出映射关系，需要设置合理的训练次数及网络误差最大值。经过反复计算，本文使用的BP神经网络最大训练次数为1000，网络误差选用网络输出和期望输出的均方差，并设置其最大允许值为2，采用L-M优化算法对气动人工肌肉的BP神经网络静态模型进行训练。在Matlab中调整各参数后，将收缩和拉伸过程中测得的气压、位移和输出拉力离散数据分别代入神经网络进行训练。

2.2BP神经网络检验及误差分析

通过训练的BP神经网络预测气动人工肌肉输出拉力，在150～750kPa每间隔100kPa测得收缩和拉伸过程中实测力、预测力与收缩率关系分别如图4和图5所示，在此过程中实测力与预测力的相关系数如表1所示。

从两图中可以看出，预测值与实际测量值基本重合，在低压区有微小偏移（图4中的250kPa；图5中的150kPa和250kPa），表1中任何气压下的拟合值与实测值相关系数都非常高，对比参考文献[3]中的相关性有了很大提高。

图4　收缩过程中测量值与BP神经网络拟合值比较

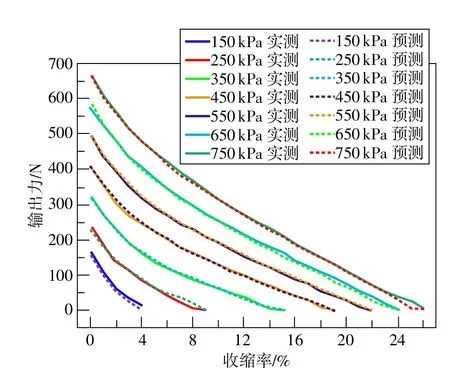
图5　拉伸过程中测量值与BP神经网络拟合值比较

收缩和拉伸过程中，在150～750 kPa每间隔100kPa测得预测值与实测值的误差率分别如图6和图7所示。在低压区（图6的150kPa，图7的150kPa和250kPa），由于输入到网络中训练的数据比较小，导致低压区的误差率很大。在收缩和拉伸的较大范围内误差率比较低（图6中750kPa下，收缩率在0～22%范围内，误差率基本为0；图7中450kPa下，收缩率在0～16%范围内，误差率基本为0），但当达到极限收缩率时（图6中气压为750kPa、收缩率＞22%的区域；图7中气压为450kPa、收缩率＞16%的区域），误差率突然增大，这是由于气动人工肌肉在达到最大收缩率情况下，输出力非常小（接近于0），预测力微弱的变化都会导致误差率陡然升高。

表1　测量值与BP神经网络拟合值相关系数

图6　收缩过程中的误差率

图7　拉伸过程中的误差率

3　结束语

1）将气动人工肌肉在100～800 kPa得到的3个特性参数代入到BP神经网络进行训练后，BP神经网络预测150～750kPa的输出力与试验测得输出力相关性非常高，能够达到0.99以上。

2）在150～750 kPa，BP神经网络预测的输出力与试验测得输出力的误差率在收缩开始较大范围内维持在较低水平，而当达到收缩极限时误差瞬间增长，在模型实际应用中，收缩极限位置不能够被使用。

3）与功能原理、力平衡和直接拟合的静态建模相比，BP神经网络建模简单，不需要复杂的理论推导即可获得相对精确的模型，并且在相关性等指标上优于其他静态模型。

[1]Chou C P，Hannaford B.Measurement and modeling of McKibbenpneumaticartificialmuscles[J].IEEE Transactions on Robotics and Automation，1996，12（1）：90-102.

[2]Ferraresi C，Franco W，Bertetto M A.Flexible pneumatic actuators:a comparison between the mckibben and the straightfibresmuscle[J].JournalofRoboticsand Mechatronics，2001，13（1）：56-63.

[3]于海涛，郭伟，谭宏伟，等.基于气动肌腱驱动的拮抗式仿生关节设计与控制[J].机械工程学报，2012，48（17）：1-9.

[4]田社平，丁国清，颜德田，等.人工肌肉系统神经网络建模与控制[J].中国生物医学工程学报，2003，22（4）：300-308.

[5]沈伟，施光林.基于气动人工肌肉的自适应模糊小脑模型神经网络位置跟踪控制[J].上海交通大学学报，2012，46（4）：579-583.

[6]高建英，彭光正，范伟，等.基于BP网络的气动人工肌肉位置跟踪的研究[J].液压与气动，2004（5）：5-7.

[7]王冬青，王钰，佟河亭，等.气动人工肌肉手臂的神经网络Smith预估控制[J].控制工程，2012，19（2）：254-257.

[8]董长虹.Matlab神经网络与应用[M].北京：国防工业出版社，2007：77.

[9]孙增圻，邓志东，张再兴.智能控制理论与技术[M].北京：清华大学出版社，2011：201-205.

Application of BP neural networks in force prediction of pneumatic muscle actuators

GU Baotong，LIU Kai，MA Tao
（College of Mechanical and Electrical Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

To find out the function relationship among force，pressure and displacement in static models of pneumatic muscle actuators，the trained BP neural network is used to predict the force of pneumatic muscle actuators in the paper.To be specific，these data obtained through quasi-static experiment are trained in the BP neural network to get a BP neural network-based static model for pneumatic muscle actuators.Prediction results show that the correlation coefficient between the predicted and experimental force is higher than 0.99 and the error rate is confined in a relative low level for a wide range of contraction.The static model is therefore proven feasible.

pneumatic muscle；actuator；BP neural network；output force；prediction

A

1674-5124（2015）12-0115-04

10.11857/j.issn.1674-5124.2015.12.028

2015-06-15；

2015-08-20

国家自然科学基金项目（51405229）江苏省自然科学基金项目（BK20151470）南京航空航天大学基本科研业务费资助项目（NS2013049）

顾宝彤（1989-），男，江苏如皋市人，硕士研究生，专业方向为仿生机器人。

刘凯（1981-），男，江苏淮安市人，副教授，博士，研究方向为仿生机器人、数控技术。