基于椭球假设的MIMU现场标定方法
翟子雄,张丕状,张煜林
(中北大学仪器科学与动态测试教育部重点实验室,山西 太原 030051)
基于椭球假设的MIMU现场标定方法
翟子雄,张丕状,张煜林
(中北大学仪器科学与动态测试教育部重点实验室,山西 太原 030051)
微惯性测试单元(MIMU)中测量组合的测量准确度直接影响姿态测试系统姿态解算的准确度,根据微惯性测量组合任意静态位置3个轴测量模值为固定值,提出一种基于椭球假设的MIMU现场快速标定方法。通过分析微惯性测量组合的误差模型,对其在不同姿态下的测量数据进行椭球拟合,快速得到全部标定参数。试验结果表明:该方法可在没有精密标定设备的条件下现场标定,操作简便、快速,准确度可以提高3个数量级,满足导航解算的准确度要求。
椭球假设;微惯性测试单元;现场标定;零偏;灵敏度;非正交
0 引 言
针对姿态测试系统小型化、轻量化、低功耗的需求,MEMS惯性测量组合的发展使得研制这种姿态测试系统成为可能[1]。微惯性测量组合(MIMU)的测量性能将直接影响姿态测试系统姿态解算的准确性;然而,微惯性测量组合单元的自身参数会随着时间、环境、温度的变化而改变[2-3]。其中,加速度传感器和陀螺仪的零偏表现最为明显,测量时间不同则所测结果不同,并且会不断漂移。那么系统的惯性测量组合在现场试验环境中的性能参数和实验室转台标定的参数会有很大不同,如果使用实验室标定的参数会产生较大的解算误差,影响姿态的解算准确度[4],因此需要一种现场标定方法[5]。
MIMU传统的标定方法有十二位置标定法[6]、静态多位置法[7],这些微惯性测量组合标定方法依赖实验室设备,很难进行现场准确标定;而文献[8]的方法虽然可以现场标定,但借助于转台测量结果,加速度计和陀螺仪的非正交误差角没有考虑进去,使得传感器输出的标定结果并不准确。因此,本文提出一种不依赖精密标定设备,每次试验前能够现场对微惯性测量组合进行快速准确标定的方法。该方法在对三轴加速度传感器和陀螺仪标定时,分别以某一位置的重力场和地球自转角速度为固定值,通过椭球拟合对MIMU中各惯性传感器的零偏、灵敏度、非正交误差角进行现场快速标定,准确度较传统方法可以提高3个数量级,完全满足导航系统对MIMU的准确度要求。由于加速度传感器和陀螺仪标定方法基本相同,本文以加速度传感器为例进行现场标定。
1 MIMU中加速度传感器误差模型
加速度传感器3个测量轴存在测量性质差异,而且3个测量轴也无法保证两两正交,因此三轴加速度传感器误差模型主要是由零位误差、灵敏度误差和安装误差组成。零位误差可以表示为

式中gx0,gy0,gz0分别为x轴、y轴、z轴的零位偏差。
灵敏度误差是由于3个轴信号的放大电路特性不同引起的,可以表示为

式中Sn为加速度传感器的额定灵敏度,Sx、Sy、Sz分别为3个轴的灵敏度。
理想情况下,加速度传感器的3个轴是完全正交的,但在传感器制造过程中不能保证3个轴两两正交,从而产生非正交误差[9]。假设加速度传感器z轴和正交坐标系的zm轴完全重合,其他两轴与正交坐标系的夹角分别为α,β,γ,如图1所示。
非正交误差可表示为

通常,厂家提供的三轴加速度传感器非正交误差角度<0.5°。因此可以对式(3)进行化简。综合考虑加速度传感器误差,真实加速度ge和测量值gm之间的关系如下:
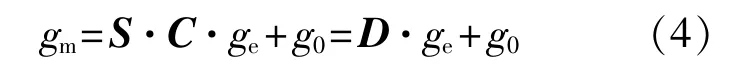
其中

其中

2 椭球拟合法
三轴加速度传感器坐标系O-xbybzb与地理坐标系O-xgygzg关系如图2所示,重力矢量g垂直向下,θ、φ分别表示载体的俯仰角和滚转角。某姿态下加速度传感器的测量值为A=(ax,ay,az)T,重力矢量在加速度传感器各轴的分量为

图2 三轴加速度传感器坐标系与地理坐标系关系示意图

在无误差的理想情况下,测量值A满足下式:


一般的二次曲面方程可表示为

的系数矩阵;

令I=a+b+c,J=ab+bc+ac-f2-e2-d2,如果4J-I2>0,式(10)必为椭球。若取为n组加速度的测量值。
定义:

则拟合椭球到测试点的问题可转化为如下约束问题:

也可表示为

其中D=(X1,X2,…,Xi),且根据文献[10]的椭球拟合的最小二乘法算法可唯一确定椭球系数向量V。
根据椭球系数,利用解析法即可求出误差参数(ge取当地重力加速度)。


将参数误差代入式(5),得到三轴加速度传感器的误差补偿模型并对测量值进行标定。
3 实验结果与分析
为了验证上述标定方法的可行性和标定结果的有效性,将三轴加速度传感器固定在三轴位置转台上,旋转转台,采集不同姿态下的三轴加速度数据,标定位置应尽量覆盖椭球的各个方向,每个测试位置静止采集20s。选取20个姿态采集三轴加速度传感器数据作为测量值进行椭球拟合,得到椭球全部误差参数,利用式(5)对加速度传感器的误差进行补偿,补偿结果如图3所示,其中虚线代表原始加速度传感器误差、实线代表补偿后的加速度传感器误差。

图3 三轴加速度传感器20组数据补偿误差
图中加速度传感器最大最小绝对误差由标定前的0.4077m/s2减小到0.0031m/s2。均方根误差由标定前的0.1247m/s2减小为7.023×10-4m/s2,准确度可以达到10-3m/s2。
传感器处于水平位置时,加速度传感器x轴和y轴应该为零,z轴感应重力加速度,将实验室转台标定参数和现场快速标定的参数应用到加速度传感器标定,经过实验室转台标定和现场标定后的三轴输出与未经过补偿的三轴输出对比曲线如图4所示。没有经过补偿的三轴输出会有较大误差,而经过椭球拟合现场标定后的准确度会逼近于转台标定结果。
4 结束语
本文分析了微惯性测量组合中加速度传感器任意姿态下的误差模型,利用椭球拟合可以求出椭球参数,进而求得加速度传感器的零位、灵敏度、非正交误差角,并对MIMU的输出进行补偿。试验结果表明,该测试方法可在不需要外界参考基准下现场快速测试,操作简单易行,经过标定后的三轴加速度传感器精度可以提高3个数量级,具有较好的工程应用价值。该方法同时适用于其他三轴矢量传感器的标定工作,如三轴磁传感器等。

图4 三轴加速度输出标定效果比较
[1]杨淑洁,曾庆双,伊国兴.低成本无人机姿态测量系统研究[J].传感器与微系统,2012,31(2):15-18.
[2]刘俊,石云波,李杰.微惯性技术[M].北京:电子工业出版社,2005:296-300.
[3]李杰,洪惠惠,张文栋.MEMS微惯性测量组合标定技术研究[J].传感技术学报,2008,21(7)1169-1173.
[4]刘锡祥,徐晓苏.惯性测量组件整体标定技术[J].中国惯性技术学报,2009,17(5):568-576.
[5]毛友泽,张海.无依托状态加速度计的新型标定方法[J].北京:北京航空航天大学学报,2011,37(1):124-126.
[6]陈弯弯,陈智刚,付建平.MEMS微型惯性测量组合的标定[J].仪表技术与传感器,2014(12):37-38.
[7]田晓春,李杰,范玉宝,等.一种微惯性测量单元标定补偿方法[J].传感技术学报,2012,25(10):1412-1415.
[8]范玉宝,李杰,张晓明,等.基于椭球拟合的微惯性测量组合现场快速标定方法 [J].传感技术学报,2011,24(11):1548-1550.
[9]龙达峰,刘俊,张晓明,等.基于椭球拟合的三轴陀螺仪快速标定方法[J].仪器仪表学报,2013,34(6):1300-1305.
[10]Li Q,Griffiths J G.Least squares ellipsoid specific fitting[C]∥ProceedingsoftheGeometricModelingand Processing,2004:335-340.
Field calibration of MIMU based on ellipsoid hypothesis
ZHAI Zixiong,ZHANG Pizhuang,ZHANG Yulin
(Key Laboratory of Instrumentation Science&Dynamic Measurement of Ministry of Education,North University of China,Taiyuan 030051,China)
Whether a measurement unit in MIMU is measured accurately can directly affect the attitude calculation of an attitude testing system.So,it is important to calibrate the measurement units quickly and accurately.A MIMU field fast calibration method has hence been proposed based on ellipsoid hypothesis and a fixed value-three axis measurement mode data in any static position.In line with the analytical results of a MIMU error model,all the calibration parameters wereobtainedviaellipsoidfittingofthemeasurementdataacquiredindifferentpostures. Experimental results show that this simple and rapid field calibration method can be used in the environment without precision calibration to improve the MIMU accuracy by 3 magnitudes,thus satisfying the accuracy requirement of navigation calculation.
ellipsoid hypothesis;MIMU;field calibration;zero bias;sensitivity;non-orthogonal
A
1674-5124(2015)12-0025-03
10.11857/j.issn.1674-5124.2015.12.007
2015-04-15;
2015-06-03
翟子雄(1990-),男,山西太原市人,硕士研究生,专业方向为惯性导航技术、信号与处理。

