中国离岸市场利率期限结构特征研究——基于面板宏观金融模型的分析

闵 敏，丁剑平，2，3

（1.上海财经大学 金融学院，上海 200433；2.上海国际金融中心研究院，上海 200433；3.上海市金融信息技术研究重点实验室，上海 200433）

一、引言与文献综述

随着我国综合国力的不断增强，人民币国际化背景下的利率市场化改革与金融市场开放逐渐成为了焦点。综观发达经济体，离岸金融市场的建设与发展是其主权货币国际化不可或缺的阶段。虽然我国人民币离岸市场建设的时间较短，但是研究其利率期限结构的特征具有不容忽视的重要意义：首先，离岸市场与在岸市场具有不同的政策背景和微观结构，研究其利率期限结构的动态演变特征有助于把握在岸利率市场化的路线和方向，可为利率市场化改革提供参考；其次，通过与在岸市场已有相关研究的对比，可以进一步挖掘不同市场之间的结构异同，从而更加深入地理解市场运作机理；最后，利率市场之间存在分割，一般分为侧重经贸需求的短期货币市场和侧重投资需求的中长期债券市场，而研究利率市场内部的差异有利于发现离岸市场建设发展过程中存在的问题，从而更好地为中国离岸与在岸市场的发展提供帮助。

香港离岸市场是目前最主要的人民币离岸中心之一。目前关于其与在岸市场互动影响的研究集中于分析汇率和单期利率的引导关系，如无本金交割远期（Non－deliverableforward，NDF）或无本金交割利率互换（Non－deliverableinterestrateswap，NDIRS）与汇率的关系（冯永琦，2012），而针对整个利率市场的研究非常少。安佳等（2013）利用中国香港和上海的银行间同业拆借利率以及中国香港人民币存量数据分析得到，两岸市场存在长期均衡关系，而不存在相互引导机制；Loechel等（2013）利用动态Nelson－Siegel模型（以下简称NS模型）对两岸国债利率市场的主要期限结构因子与宏观经济变量进行了分析，得出决定两岸市场因子的条件互不相同的结论，同时验证了两岸市场之间不存在利率上的溢出效应。可见，关于离岸市场利率期限结构的研究无论是在具体问题的分析还是在方法的运用上都存在局限，缺乏系统而全面的动态分析。

关于在岸利率期限结构的研究非常丰富，目前主流的研究已经开始进行宏微观相结合的互动分析。例如，Diebold和Li（2002）将静态NS模型在固定衰减系数的情况下基于三个参数构建了动态模型，但由于解释变量缺乏经济结构信息，这类动态化的静态模型缺乏宏观经济意义。而Ang和Piazzesi（2003）通过拓展债券定价理论，首次将通胀率等宏观经济变量通过无套利定价核引入到仿射利率期限结构模型（Duffle和Kan，1996）中，以更加方便地研究利率期限结构与宏观经济变量之间的互动关系，开启了宏观金融模型（Marco－finance model）的先河。

宏观金融模型可以很好地兼顾微观演变和宏观分析，发展应用已非常广泛，被大量应用于利率期限结构特征研究以及与宏观经济的互动分析中。例如，Ichiue（2004）针对美国的研究表明，GMM估计结果优于Ang和Piazzesi（2003）两步法估计结果，并提出了一套宏微观变量互动分析的方法框架。石柱鲜等（2008）参考Ichiue（2004）的模型设定，对同业拆借期限结构与宏观变量的互动关系进行了研究。孙皓和石柱鲜（2011）借鉴Oda和Suzuki（2007）的结构化模型，对同业拆借市场基于宏观风险的估计结果进行了分解，得到利率期限的预期成分和风险溢价成分。而魏玺（2008）对我国交易所和银行间债券市场利率期限结构与主要宏观经济因素进行了动态分析，发现两者之间存在相关关系。

离岸市场本质上是在岸市场的延伸，在岸是离岸的“根基”。同时，中国在岸市场并没有完全开放，它是一个相对合适的“参考系”而不用担心内生性问题。因此，本文基于宏观金融模型框架，以在岸经济为基础，通过回答以下3个问题来揭示中国离岸利率市场的特征。

第一，在岸经济变化对离岸利率市场有何影响？有研究认为，经济利好会引起离岸利率上升（石柱鲜等，2008）。针对日本离岸市场的研究却发现，在岸经济繁荣会导致离岸市场的资金存量增多（许祥云，2013）。其背后的机理可能是进口消费、本币贸易扩张甚至境外旅游等贸易形式增多，也可能是在岸资本的直接流出。无论何种形式都会导致资金的价格（即利率）下降。但中国和日本不同，中国的在岸金融市场并没有完全开放，资本流动还存在限制，那么中国在岸经济对人民币离岸市场的影响是否存在类似日本的结果呢？

第二，离岸利率市场对在岸市场有“反馈”吗？期限结构蕴含着丰富的经济信息，Ichiue（2004）发现美国债券市场对宏观经济有一定的预测能力，石柱鲜等（2008）发现SHIBOR市场也存在这个现象。对于离岸市场，一方面，市场化的运作、国际化的背景以及专业化的参与者都能给价格信息“加分”，增加预测能力；但另一方面，由于中国在岸市场管制，离岸人民币回流渠道体系尚未完善，离岸人民币目前还是一个相对独立且规模不大的“池子”。就像二级市场上交易的股票一样，交易者偏好甚至市场投机性都可能干扰公司基本面信息在价格上的反映，离岸的资产定价也可能存在这个问题。那么在当前的人民币离岸利率市场中，究竟哪种逻辑占主导呢？

第三，在岸经济在离岸利率定价上起到什么作用？孙皓和石柱鲜（2011）发现，在岸市场利率中除了包含自身的预期风险外，还有来自宏观经济的风险溢价。这可能是因为在岸投资者“没得选”，从而把宏观经济的变化看作不确定因素之一。而离岸市场的产生源于离岸投资者对在岸本币的需求。如果把在岸经济看作本币离岸资产的“基本面”，那么一种逻辑是，“基本面”好是投资者愿意持有的原因，会减少资产的风险。但这里同样存在第二个问题中的分析逻辑：如果出现其他需求偏好或者预期升值性投机，则投资者同样可能愿意持有，比特币就是一个比较典型的例子。①比特币并无“基本面”可言，但它在塞浦路斯银行危机中充当避险保值货币，后亦因高投机回报而遭疯抢。那么，人民币离岸利率市场中会存在这样的在岸“利好”现象吗？

经过四年多的发展，中国香港离岸市场的数据已趋于稳定。因此，本文根据离岸市场特性来构建全新的面板宏观金融模型（Panelmacro－financemodel，PMFM），通过考察中国香港HIBOR人民币市场和离岸人民币债券市场来回答上述3个问题。同时，出于完整性考虑，我们将在岸国债市场因子化，作为在岸利率因子，并综合在岸的其他宏观因子，与离岸利率市场一起纳入分析框架。

二、模型建立

（一）模型构建

按照朱波和文兴易（2010）的分类方法，根据宏观经济模块有无结构化信息约束，宏观金融模型被分为简约化模型和结构化模型。Ang和Piazzesi（2003）的模型是典型的简约化模型，侧重实证分析，其因子约束少，但隐变量缺乏一定的经济理论依据；而结构化模型大多含有复杂结构方程，侧重模拟分析，如Bekaert等（2010）基于新凯恩斯宏观经济模型的利率期限结构模型。离岸市场的经济基础复杂，无法直接使用现有的理论模型。因此，本文在简约化模型的基础上构建了一个适用于离岸市场的分析框架。

首先，与以往直接使用息票处理的研究不同，本文使用四因子Nelson－Siegel－Svensson模型（下文简称NSS模型）对离岸和在岸债券市场分别建模。我们首先通过拟合在岸市场固定衰减系数，得到描述该市场动态规律的结果并引入主模型，然后通过拟合离岸市场非固定衰减系数，获得更高的精度作为具体期限进行分析。其次，考虑到离岸市场的特性，本文进一步引入面板数据模型进行无偏性修正，以提高后续分析的稳健性。最后，出于精度和稳健性考虑，本文使用GMM方法进行估计。②本文使用Matlab来拟合NSS模型和进行GMM估计，并使用两阶段NW方法来保证GMM 估计的渐进一致性。传统的宏观金融模型估计方法有两步法和GMM方法两种（Kim，2009）。两步法计算量较小，并使用极大似然估计。但利率数据不服从正态分布，极大似然估计的假设过于严格；此外，由于收敛性问题，当变量较多时不得不对估计参数做出限制（Ang和Piazzesi，2003）。而GMM估计的假设较少，但由于待估矩条件较多，目标函数不光滑而呈阶梯状（Kim，2009），因此对优化算法和计算速度的要求较高，实现难度较大。离岸市场数据的长度较短，从而必须考虑精度，否则会影响后续研究结果的可靠性。

（二）模型设定

1.NSS模型。标准的NS模型是一个类似动态利率方程的常微分方程，用它可以描绘递增、递减、水平和倒置四种不同的利率期限结构。为了更好地拟合复杂的收益曲线，如驼峰形和V字形曲线，Svensson（1994）对NS模型进行了扩展，添加了反转因子。由此得到的未来θ时刻的零息利率为：

其中，β0、β1、β2和β3是系数，分别表示水平、斜率、曲度和反转因子，浓缩了期限结构的主要信息。τ1和τ2是衰减系数。由于真实债券市场以附息债券为主，大多采用净价交易，因此报价数据不能直接用于估计参数。对此，本文参考以往的文献，直接展开所有债券每期的贴现现金流，按照NSS模型折现至当期，然后通过最小化误差来估计参数。因此，计算时实际使用的公式为：

其中，W为拟合权重。考虑到久期对期限结构的影响，我们以修正久期的倒数作为权重，对每个交易日的数据进行非线性优化来估计参数。而为了权衡拟合精度和参数稳定性，我们采用在岸市场固定τi估计、离岸市场自由估计来满足具体的模型需求。

2.无隐变量的宏观金融模型。我们接下来构建离岸与在岸市场的仿射利率模型，将一个经济体分为宏观经济和两个同币异市利率部门。本文参考Ichiue（2004）的研究来构建一个无隐变量的仿射模型，设kn＝（bncn）T，则有：

其中，Xt表示宏观经济部门，Zt＝（β0tβ1tβ2tβ3t）T则代替宏观金融模型中的隐变量，表示在岸市场的利率部门。为了简化模型，假设Xt和Zt分别服从一个VAR（1）过程且独立，可表示为：

为了更好地对VAR进行结构性解释，假设εt和ξt都具有变量顺序传递的递归结构，即εt＝∑bμbt，ξt＝∑cμct。在此基础上，考虑一个离岸市场无套利①考虑到在岸利率市场管制，人民币离岸市场的无套利假设更加合理。的债券资产定价过程：

其中，Mt＋1是服从对数正态分布的随机贴现因子，pnt是t时刻存续期为n的债券价格，且有p11＝1。设λ1为准对角矩阵，λt＝λ0＋λ1（XtZt）T，则有：

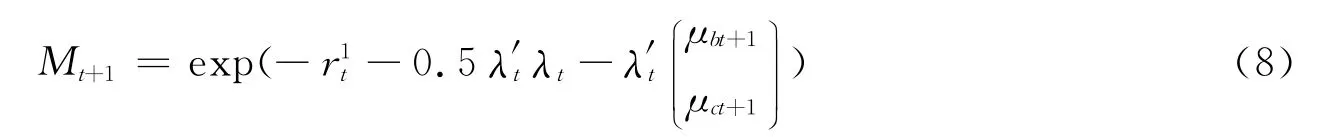
根据利率模型，令An＝－nan，Kn＝－nkn，Bn＝－nbn，Cn＝－ncn，则零息债券价格又可表示为：

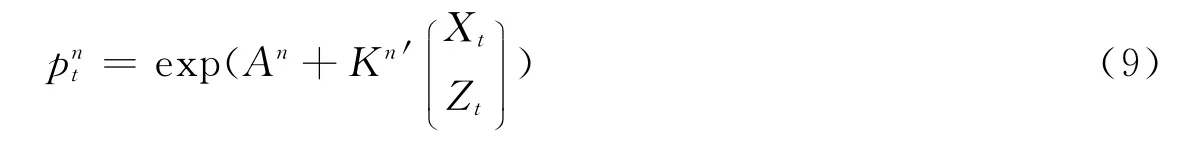
按照无套利模型的推导，设λ0＝（λ0bλ0c）T，λ1b和λ1c分别为λ1这个准对角矩阵的组成方阵，则各系数满足如下的递归方程：

其中，b1和c1分别表示r1t即第一期针对Xt和Zt的系数。而对于离岸市场，如果使用债券市场数据做完全期限拟合，则最终模型可以表示为：①本文不以利率作为解释因子，因而不对第一期的拟合进行强制约束。

其中，Δ为最小步长，Zht为离岸市场的动态NSS模型参数向量。对于每个时刻t，τ1t、τ2t和Zht都是使拟合误差最小的优化结果。

3.宏观金融模型的面板化改进。以往文献的期限拟合只有误差之和最小的约束条件，而没有考虑相关性。期限结构数据具有“小n大t”的面板结构，如果时间和期限两个维度上的残差项与解释变量相关，则估计结果将是有偏的。因此，本文增加了一个来自期限维度的固定效应，认为各期限之间有与解释变量相关的固定成分，则有：

其中，αt为固定效应。由此，我们估计的是除去基期外的差分项，如t时刻m期和n期的差分项：

受益于宏观金融模型的递归设定，差分后的式（16）并没有丢失an和am，而且式（15）实质上没有常数项，完全不影响整体模型的估计，反而准确地滤出了固定效应。但模型设定使实际估计时还需要使用式（15）来估计a1和k1，因此如果存在固定效应，则该面板模型的估计不能做到完全无偏，但无偏性要大大优于直接估计原始模型。①根据GMM估计的原理，在隔期差分的基础上适当增加跨期差分一并进行估计，可以减少式（15）的有偏性。

如果存在固定效应，则说明离岸市场的期限结构存在在岸变量无法解释的共同趋势。虽然离岸市场是在岸市场的延续，但正如象棋中“过河的卒子”，离岸国际化的舞台赋予了该市场新的意义。市场参与者的不同、监管制度的差异、其他币种资产的竞争以及跨越地域的信息不对称都可能导致离岸市场有自己“不一样的声音”。

三、模型估计

（一）数据说明

考虑到中国CNH债券市场交易活跃较晚以及数据的可得性，本文选取了2012年7月至2014年6月的在岸和离岸周度数据以及同期的在岸国债数据。②由于离岸债券市场发达，而且离岸发债的国内企业信用良好、资金雄厚，因此离岸市场不仅包含13只国债，而且扩展到43只人民币债券。但在国内，国债市场是主体，所以我们只使用国债数据。拟合优度结果见表1。

表1 在岸与离岸人民币债券市场拟合情况

在岸市场人民币债券选取对应期限的交易所交易国债，NSS衰减系数按照误差最小原则进行变步长全空间搜索，最终得到最优衰减系数为［2.5，0.05］，这与已有文献的计算结果差别不大。从表1中可以发现，拟合情况较好，基本可以涵盖整个信息集。

本文中的宏观数据包括经季节调整的实际GDP增长率gt、M2增长率mt和CPI增长率πt，并假设它们服从上述的传导结构，且均经过年化处理。本文选择了两个离岸利率市场，分别是HIBOR人民币市场和CNH债券市场；同时，考虑到市场分割情况和各市场主要期限的分布情况，我们分别选择了1周、2周、4周、8周、12周、24周和48周以及48周、60周、72周、84周、96周、108周和120周各7个期限。本文数据来源于Bloomberg，并结合Wind EBD进行校验。

ADF检验表明，3个宏观变量都是I（0）过程，属于平稳序列，可以构造VAR（1）模型，而4个在岸期限因子都是I（1）过程。Johansen协整检验表明，4个I（1）过程的期限因子有且最多有一个滞后一阶的协整关系，单独估计模型稳定。③受篇幅限制，具体检验结果未报告。

（二）分市场估计

1.HIBOR人民币市场的估计。HIBOR人民币市场的主要部门共有64个变量，加上估计基期和第一期所需的8个参数，共72个变量。而考虑到国内利率市场和离岸市场的相关性，我们只选用宏观经济部门作为工具变量。同时，出于模型简洁性和可识别性考虑，我们分别加入了各期跨期利差、期末期初利差和期末期中利差，矩条件也为72个。估计结果见表2。

从表2中可以发现，GMM估计的模型非常显著，VAR模型几乎都是显著的，这与OLS模型相比更加稳健。而金融部门市场风险价格的显著性也不错，与Ichiue（2004）的结果类似。但属于短期的HIBOR人民币市场对于在岸市场的曲度反转因子的时变效应都不显著，说明短期离岸市场的利率结构变化较为单一，在岸的曲度因子足以描述其市场的复杂结构变化，这符合常识。

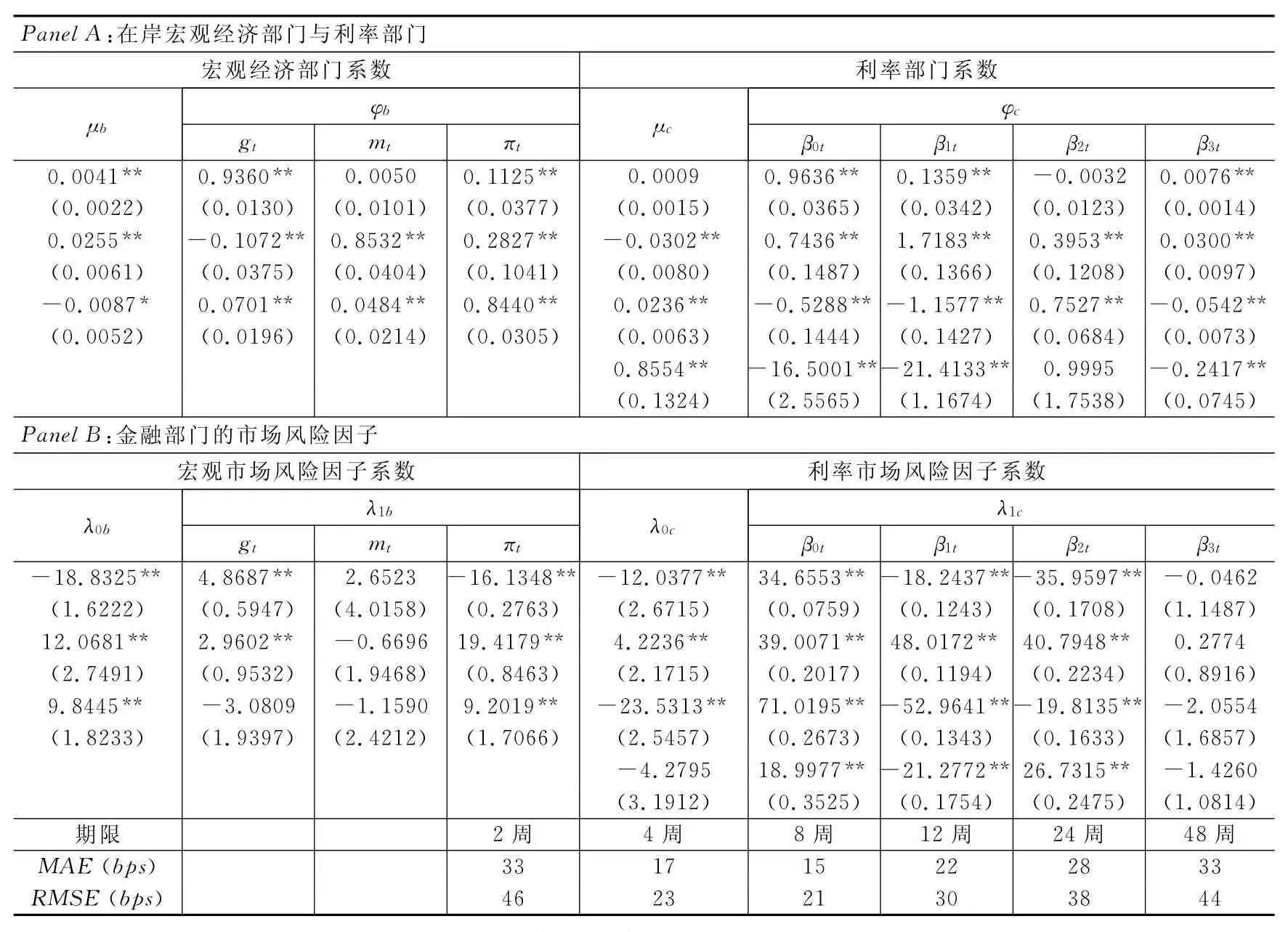
表2 HIBOR人民币市场估计

图1 HIBOR人民币市场固定效应序列（αt，含95%置信区间）

离岸期限拟合误差的平均绝对值误差（MAE）和均方误差平方根（RMSE）也显示出对于面板模型的强拟合能力。与以往使用月频数据得到的误差相比，周频数据的结果可以接受。此外，固定效应有多处较为显著，而且具有明显的聚集性和持续性，因此它在这个市场的期限结构中是不容忽视的，这也证明了引入面板模型的必要性。

2.CNH债券市场的估计。CNH债券市场的主要部门也有64个变量，加上估计基期所需的8个参数和迭代所用的第一期的8个参数，共80个变量。与HIBOR人民币市场不同，CNH债券市场的短期利率与平均久期差距较大而无法作为首项使用。本文延续以往研究惯例，借用拆借市场周利率作为首项，但迭代从CNH债券市场最短期限即48周开始。我们同样加入了各期跨期利差、期末期初利差和期末期中利差，矩条件也为80个，恰好识别模型。估计结果见表3。

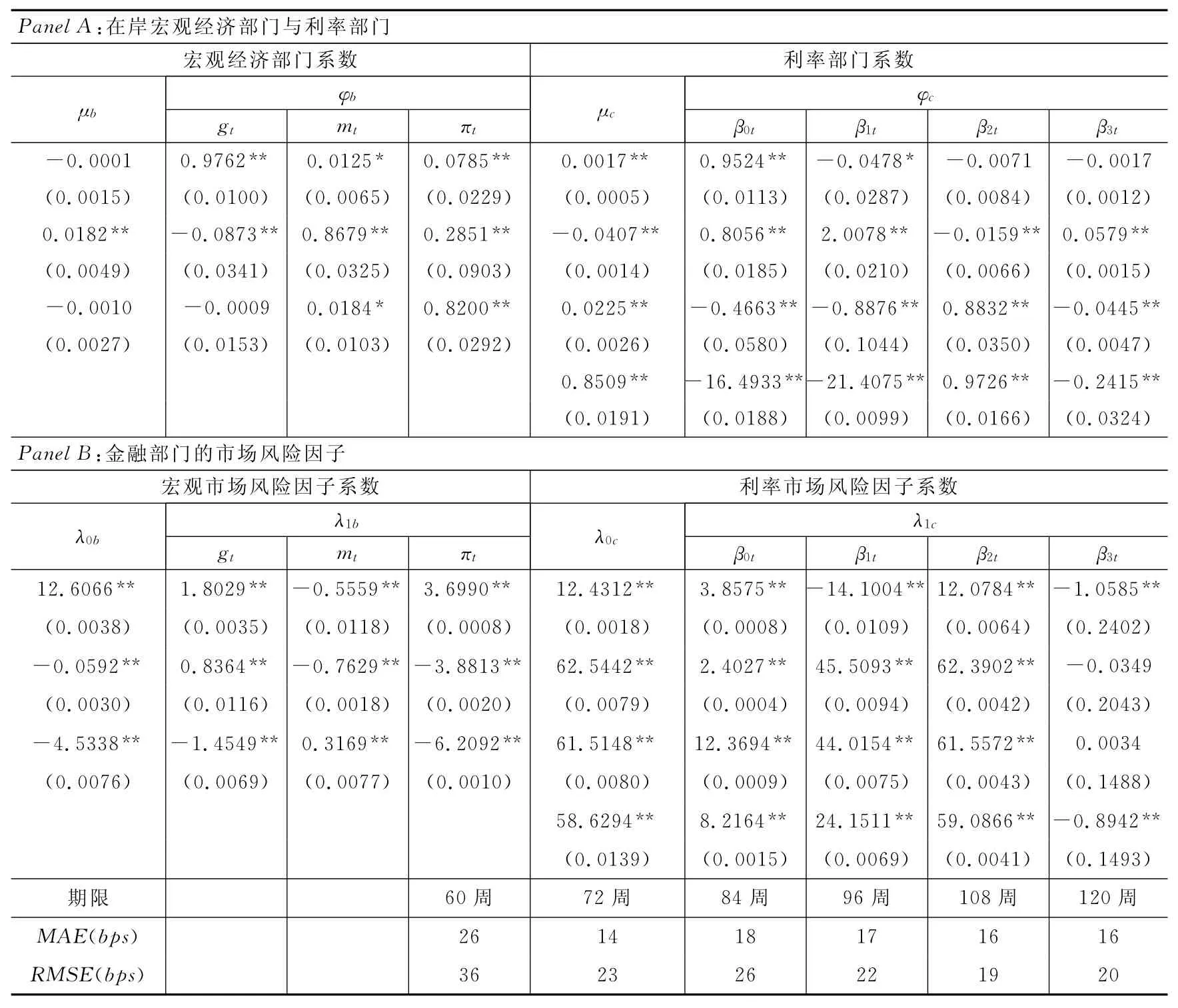
表3 CNH债券市场估计

图2 CNH债券市场固定效应序列（αt，含95%置信区间）

该市场的模型更加显著，尤其是在金融部门。这说明与短期的HIBOR人民币市场相比，中长期的债券市场与在岸债券市场有着更加密切的联系。同时，期限拟合的结果与HIBOR人民币市场类似，效果较好，而且CNH债券市场同样存在固定效应。

四、模型分析

基于上文的估计结果，本文进一步对模型进行了脉冲分析、方差分解、因子风险分解和反馈预测，①宏观金融模型不是单纯的VAR模型，本文参考Ang和Piazzesi（2003）的附录公式进行了脉冲分析和方差分解。通过回答引言中提出的三个问题来分析两个离岸利率市场的期限结构特征。

（一）在岸经济变化对离岸利率市场有何影响？①由于缺乏关于在岸利率因子对离岸期限结构影响的同类对比研究，我们在此不展开分析。

从图3中可以发现，两个离岸利率市场各个期限对宏观经济变量的脉冲反应基本上都是负向的。除了HIBOR人民币市场的2周利率对于通货膨胀的冲击有短时间的正向反应，以及人民币离岸债券市场的60周利率对于GDP的冲击为小幅的正向反应，其他基本上与石柱鲜等（2008）针对在岸利率市场的研究结果相反。这说明，虽然中国资本项目并没有完全开放，但是在岸经济可以借助贸易渠道来影响离岸市场。在岸经济的繁荣可能导致中国香港离岸人民币的增多，降低离岸市场的资金价格，从而出现和日本一样的情况。

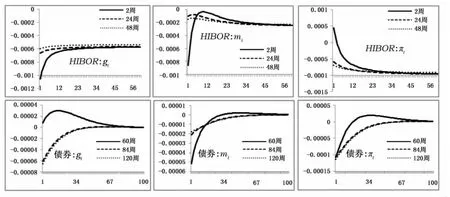
图3 HIBOR人民币市场与CNH债券市场对于在岸宏观因子的脉冲反应

需要注意的是，虽然与HIBOR人民币市场的结果类似，但是在岸宏观经济对CNH债券市场的影响幅度远小于HIBOR人民币市场，这说明CNH债券市场对于宏观经济的反应不如HIBOR人民币市场敏感。

（二）离岸利率市场对在岸市场有“反馈”吗？

针对这个问题，本文对离岸利率期限结构进行了预测能力分析。Ichiue（2004）及石柱鲜等（2008）利用相关系数来研究利率期限对解释因子的预测情况，具体如下：

其中，corr函数表示皮尔森相关系数，为t时刻未来h期的模型预测值，与为同一时刻第n期和第m期的预测值。考虑到与真实数据接轨，本文使用去除噪音影响的未来期拟合值来替代。同时为了简化结构，去除复杂的利差组合，本文直接研究期限结构本身，则计算公式变为：

在此基础上，我们再考察反映市场特有特征的固定效应对预测效果的影响。结果发现，HIBOR人民币市场的期限结构对在岸宏观因子有较好的预测能力，对GDP增长率的预测能力最高接近70%，对通货膨胀最高约为24%。但受市场分割影响，对在岸利率四个因子的预测能力一般。此外，在大部分期限结构下，含有固定效应的预测效果更好。①受篇幅限制，这里只报告了含固定效应的预测情况。CNH债券市场的预测能力则主要体现在通货膨胀（最高为35%）和水平因子（最高为29%）上，其他因子结果不如HIBOR人民币市场，当不包含固定效应时则几乎没有预测能力。

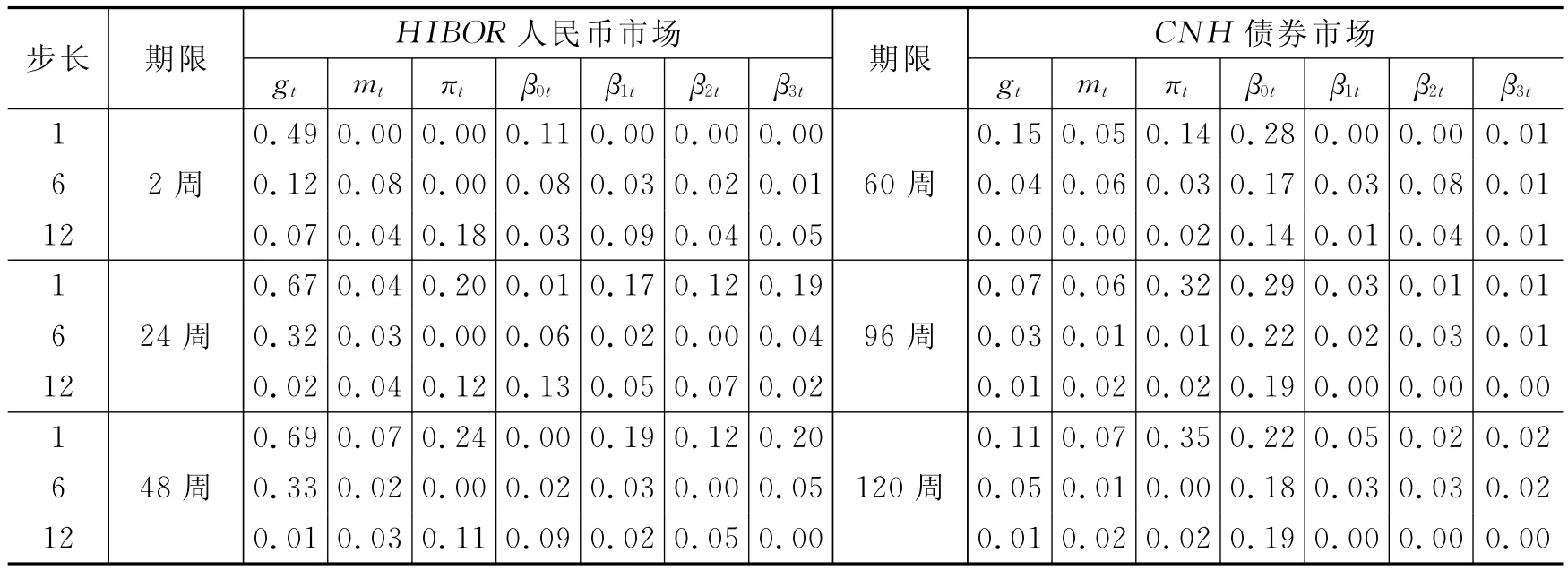
表4 离岸市场对于在岸因子的预测情况对比（含固定效应）

两个市场之间的差异非常明显。HIBOR人民币市场对于在岸经济尤其是部分宏观因子有非常强的信息回馈，甚至超过了国内SHIBOR市场，可以考虑作为在岸市场投资、政策制定的参考因素，属于来自市场化的利率修正“意见”。CNH债券市场对于在岸通胀和利率水平因子具有一定的预测能力，但弱于国内债券市场。由于存在市场期限差异而不能直接比较，如果将国内市场看作标杆，HIBOR人民币市场的“反馈”能力强于国内SHIBOR市场，而CNH债券市场则弱于国内债券市场。HIBOR市场发展相对更加成熟，期限结构中包含的有效经济信息相对更多。

（三）在岸经济在离岸利率定价上起到什么作用？

针对这个问题，本文按照孙皓和石柱鲜（2011）的方法，将金融部门市场因子的所有参数均设为零，得到预期的市场利率。而拟合的利率减去预期的市场利率即为金融部门市场因子风险溢价。其中HIBOR人民币市场的分解结果与孙皓和石柱鲜（2011）的结果类似，风险溢价结构比较稳定，但不同的是，2周利率出现了负溢价，也就是说市场风险因子反而降低了短期利率风险。这说明中国的经济情况相对于别国在离岸市场的确是“利好”的“基本面”：离岸市场中的投资者更愿意承担预期风险去持有人民币资产，在一定程度上因为它是“中国制造”。而随着期限的增加，这种现象逐渐消减，结合国内分解情况，这可能是因为交易活跃程度下降导致持有需求下降。

CNH债券市场的分解结果则与HIBOR人民币市场不同，市场因子的风险溢价无结构性，有正有负，随着期限的增加，波动变小趋于平稳。需要注意的是，CNH债券市场的60周利率在初期出现了预期风险的大幅跳跃，但实际利率变化并不大，风险溢价起到了平稳利率的作用。此外，主要期限中风险溢价为负的时期占多数，这与HIBOR人民币市场一样，表明在岸经济起到了降低和稳定离岸利率风险的作用。

（四）其他实证结果

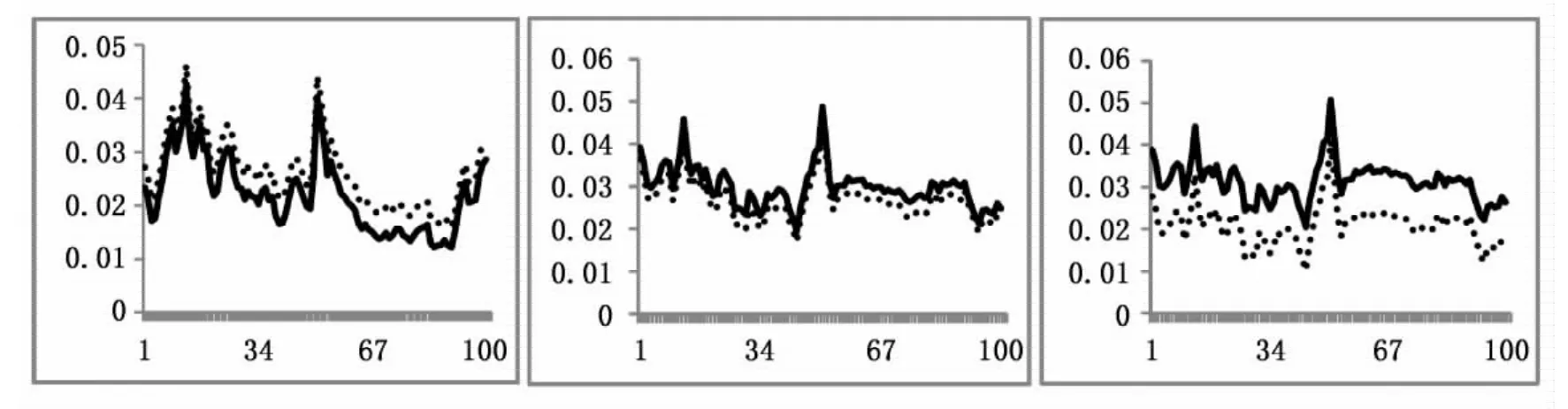
图4 HIBOR人民币市场分解

图5 CNH债券市场分解

除了上述3个主要问题外，本文进一步通过方差分解来观察主导离岸市场变化的变量贡献。结果发现，在岸经济对离岸HIBOR人民币市场各期限的作用更为平均，而对CNH债券市场各期限的解释主要集中在在岸水平和斜率因子上。从利率市场的角度来看，结合之前离岸人民币市场对在岸利率因子的预测仅集中于水平因子的结果，CNH债券市场与在岸利率市场的相互影响不对称，在岸对离岸的影响更加全面。这在一定程度上也支持了第二个问题中关于CNH债券市场发展不足的发现。

表5 HIBOR人民币市场方差分解平均情况①受篇幅限制，仅报告了主要的方差分解平均数据。

表6 CNH债券市场方差分解平均情况

五、结 论

本文以在岸经济与市场作为分析基础和研究参考，通过一个经过无偏修正、与NSS模型相结合的面板宏观金融模型，对中国离岸市场利率期限结构特征进行了系统的动态研究。本文通过与在岸利率市场的比较，发现离岸市场利率期限结构存在不同的市场特性：

首先，在岸宏观经济对离岸利率的影响可能需要考虑市场资金存量（规模）而不再仅是依靠经济数据，而在岸市场上资本项目管制的溢出效应较小。在这种情况下，利率的决定是相对的而不是绝对的，因此相关的分析思路和决策指标都需要随之改变。这对于进一步推进在岸市场的利率市场化具有参考意义。

其次，离岸利率市场的价格对在岸市场亦存在“反馈”，蕴含着丰富的信息。其中，HIBOR人民币市场的预测效果甚至优于在岸市场，显示出市场化和国际化的离岸市场的信息发现优势，因此它完全可以作为在岸市场的决策变量。而CNH债券市场的预测效果弱于国内市场，存在一定的不足。这在一定程度上表明，在经常项目完全开放而资本项目尚有限制的条件下，获得更多流动性的HIBOR人民币市场更能反映在岸宏观要素的变动。

再次，在离岸市场中，多维度的信息可提供更准确的“定向”，投资者更愿意承担一定的风险去持有人民币资产。这对于人民币“走出去”无疑是一个良好的契机。因此，在继续做好外部市场拓展的同时，相应的监管政策和红利政策也需要跟进，在保证人民币流通渠道畅通的同时要遏制非法套利和预防升值预期性投机，从而稳步实现国际化战略。

最后，HIBOR人民币市场和CNH债券市场的表现差异表明，短期的HIBOR人民币市场反映的是国际经济与贸易中对人民币的诉求，其较高的预测能力和较对称的双向影响结构揭示了该离岸市场良好的发展态势，表明人民币在国际经贸中的地位不断提高；而中长期的离岸债券市场反映的是资本市场的诉求，分析结果表明人民币在资本市场的“国际化”仍存在较大的空间，需要进一步努力。这也给在岸利率市场的发展提供了参考：资本市场的发展与繁荣单靠“市场化”是不够的，还需要相关衍生品、流通渠道以及监管发行模式等一系列配套机制的有效协同。

自2010年建立以来，中国香港两个离岸利率市场均已走出了“热身期”，成为了具有一定影响力的“风向标”。本文通过研究离岸人民币利率市场期限结构的特征，让我们“听到”了海外人民币资产发出的“不一样的声音”，同时带给我们对于市场化利率运作机制更深的理解和不同的视野。但对于其运作机理，需要更加系统而深入的研究，从而推动离岸利率市场的进一步发展，并为在岸利率市场化积累经验，共同为人民币国际化打下坚实的基础。

［1］安佳，逄金玉，王振山，等.人民币离岸在岸利差和汇差与资本跨境流动［J］.管理世界，2013，（12）：172－173.

［2］冯永琦.香港人民币离岸市场形成与发展研究［D］.长春：吉林大学博士学位论文，2012.

［3］石柱鲜，孙皓，邓创.中国主要宏观经济变量与利率期限结构的关系：基于VAR－ATSM模型的分析［J］.世界经济，2008，（8）：53－59.

［4］孙皓，石柱鲜.中国利率期限结构中的宏观经济风险因素分析——基于宏观金融模型的研究途径［J］.经济评论，2011，（3）：36－42.

［5］魏玺.引入宏观政策变量的中国利率期限结构微观研究［D］.上海：复旦大学博士学位论文，2008.

［6］朱波，文兴易.利率期限结构宏观金融模型研究新进展［J］.经济学动态，2010，（7）：101－105.

［7］Ang A，Piazzesi M.A non－arbitrage vector autoregression of term structure dynamics with macroeconomic and latent variables［J］.Journal of Monetary Economics，2003，50（4）：745－787.

［8］Ichine H.Why can the yield curve predict output growth，inflation，and interest rate？An analysis with affine term structure model［R］.Working Paper，2004.

［9］Kim D H.Challenges in macro－finance modeling［J］.Social Science Electronic Publishing，2009，91（5）：519－544.

［10］Loechel H，Packham N，Walisch F.Determinants of the onshore and offshore Chinese government yield curves［R］.Working Paper，2013.