高等数学教学中的几点注记

唐风琴，杜翠真

（淮北师范大学 数学科学学院，安徽 淮北 235000）

高等数学教学中的几点注记

唐风琴，杜翠真

（淮北师范大学 数学科学学院，安徽 淮北 235000）

探讨高等数学教学中的三个问题，包括极限的思想和方法、量与图形的统一及高等数学在经济学领域的应用，旨在改进课堂教学效果，提高学生学习兴趣.

高等数学；极限；量与图形统一

《高等数学》是理工科院校一门重要的基础课程，具有高度的抽象性、严密的逻辑性和广泛的应用性等特点.学好高等数学对许多专业后继课程的学习起到举足轻重的作用，比如《大学物理》、《化学动力学》、《数据结构》、《计量经济学》等课程就要求有较好的微积分功底.但是很多院系文理兼收，学生来自五湖四海，数学水平参差不齐，在讲授同一本教材时，老师们常感到进度困难，部分学生也觉得很困惑，学习兴趣消失殆尽，不利于其他相关专业的学习.基于以上种种问题，很多教师对高等数学教学方式及教学内容等方面做大量有益的研究.比如齐民友［1］总结微积分的发展史并对微积分的教学提出一系列的观点，鲍培文［2］探讨在高等数学教学中数形结合问题，张莲［3］总结高等数学教学中求极限的方法，杨丽贤等［4］探讨高等数学在经济领域的应用.在此基础上，本文结合实际教学经验，对极限的思想和方法问题、量与图形的统一问题及高等数学在经济领域的应用进行讨论，旨在改进课堂教学效果，提高学生学习兴趣.

1 极限的思想和方法

学习《高等数学》课程的第一个要求就是理解极限的思想，建立极限的概念.《高等数学》［5］上册以初等函数为研究对象，其内容和体系基本是建立在严格的（初等）极限理论基础之上的.如果对极限掌握不过关，这门课程的后期学习就必定面临巨大的困难.然而，对大部分刚刚步入大学的学生（尤其文科背景的学生）而言，这一要求是很难达到的.毕竟，从初等数学到高等数学，跨度很大——研究对象由常量转化为变量，研究范围由有限转化为无限.解决问题的主要手段更是产生一个飞跃——由直观的初等方法变为抽象的极限方法.许多重要的概念，均是借助极限来定义的；许多重要的问题，均是借助极限来解决的.另一方面，高中数学课程对函数和极限等内容的描述不够严格，使许多学生对这些概念的理解不够深刻，认识误区比比皆是.要想改变这一现状，避免教师在《高等数学》课程教学中花费大量时间去纠正学生的种种错误观念和认识误区，可从以下几点着手：

第一，以鼓励为手段，促进学生的学习兴趣.文理学生同堂听课，文科学生学习高等数学的心理压力更大.要特别对他们进行鼓励，鼓励他们思考和提问，提高他们的自信心，避免问题积累，差距扩大.数学是需要想象力的，而在想象力方面，文科学生并不见得会差于理科学生.

第二，在坚持极限概念严格性的基础上，尽可能赋予直观解释.必要时，甚至可以牺牲一部分严格性.直观解释可用的例子很多，不胜枚举.最重要的是利用直观解释来增强理解，揭露本质.例如，要让学生明白极限是一个无穷进行的过程，旨在描述一种变化趋势，从宏观层次到微观层次再到更微观层次，永不停止，突破初等数学的有限观念束缚.对极限的定义，如果一开始就照抄ε-δ语言，不去解释极限的背景及其本质，那么学生会完全不知所云.因此在教学中应该先讲有关背景，例子要丰富，类型要突出，提出问题并启发思考；然后总结其共同的内在特征，引出极限的思想；接下来则很自然地通过数学的方法描述极限并引导同学们进入状态，最后抽象出经典的极限定义，这样学生接受起来会容易的多.

第三，无穷小量的阶的比较，是极限理论的经典内容，更是极限教学的关键部分.面对一个一般的极限问题，结果总是可以计算出来的，比如说，等于A，但要问，这个极限为什么等于A？为什么不是B？如何解释.经验表明，如果学生弄清了无穷小量的概念及其阶的比较的原理，并学会以此来解释极限，就会对极限是什么产生更细致、更深刻的理解.进一步地，如果搞清无穷小量的概念及其阶的比较，无穷大量的概念自然就清楚，并且有关极限未定型、收敛速度、广义积分及级数的收敛等相关问题的理解也就容易多.

第四，关于极限的求法，应注重多种方法的结合.诸多单个的方法如各类初等代换、变量代换、等价无穷小（大）量的替换、L′Hospital法则以及利用两边夹法则、Taylor展开及定积分求极限等，均是极其经典并行之有效的，但对于经常碰到的较为综合或复杂的求极限问题，则需将上述各方法结合起来予以解决.

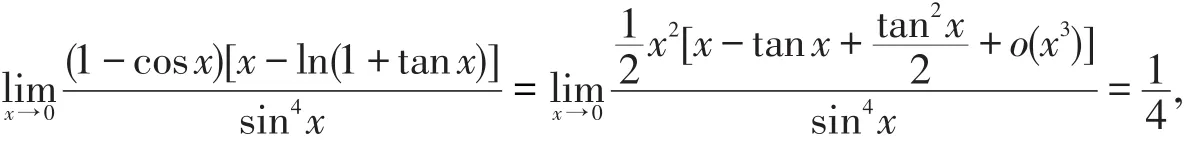
这道题显然不能通过一种方法解决，需要结合等价关系和Taylor展开才能完成求解.

第五，及时总结，不断反复，让学生逐步深化对极限的认识.极限内容讲完，一个接一个新的概念如连续、导数乃至定积分、级数等，均要求我们的教学重复地运用极限的概念.从长远来看，以极限思想作为一条主线，贯穿于《高等数学》课程教学的整个过程，不仅有利于学生温故知新，加深对极限概念的理解，熟练掌握求极限的方法，还能在一定程度上保证学生对《高等数学》课程宏观框架的把握，既见树木，又见森林，益处毋庸质疑.

2 量与图形统一问题

数学类的许多课程很讲究“量”与“图”二者的统一和结合，《高等数学》自然也不例外.在传统的数学教学中，教师往往更关注定义、公式、定理的逻辑推导而忽视它们的几何或者物理背景.要让学生感受到深奥数学公式的直观美，需在教学中做到以下几点：

第一，首先将实数与实数点、实数集与实数轴之间的一一对应关系建立起来.这是量与图形统一思想的基本出发点.就教学而言，它也是对中学数学有关内容的一个简要回顾，起着承上启下的作用.弄明白这一点，日后多变量函数中二元实数对与二维实数点、多元实数集与多维实空间的子集之间的等价性，就仅仅是形式上的推广，理解起来不成问题.

第二，在平常教学中，不少问题的描述和推导，教师应坚持利用图像加以直观解释.我们注意到，有些证明几乎是完全可以利用图像方法来完成的.即使不是如此，借助图像进行辅助分析，效果也很好.数学看起来总是抽象的，但其本质绝不抽象，学习数学不应拘泥于抽象的形式.典型的例子如中值定理类问题，若不顾几何背景，纯粹使用数学推导，结论就显得很晦涩难懂，证明自然也难以完成.即使勉强完成了证明，就数学教学的要求而言，意义也不大.问题的实际背景是什么以及结论有什么意义？二者之间有什么联系？纯粹的数学推导是回答不了这些问题.相反，若能够根据已知条件绘出图像，则一目了然.根据图像会清楚地看到，要找的那种点在什么位置？实际上，它只能存在于已知区间的某些特定的位置.接下来的任务仅仅是利用经验和技巧将其解析地“推导”出来罢.

例2 已知f（x）在（0，1）上可导，在［0，1］上连续满足f（0）=0，f（1）=1且f（x）是关于x的非线性函数.证明在（0，1）内至少存在一点η使得f′（η）＞1.

首先给出该题的理论证明.令F（x）=f（x）-x，由已知，F（x）在（0，1）上可导，在［0，1］上连续满足F（0）= F（1）=0且F（x）不恒等于0.记

以下分两种情形讨论：

（1）若M＞0，则必有x1∈(0,1)，由拉格朗日中值定理知，存在η1∈(0,x1)，使得

而F′(η1)=f′(η1)-1，故 f′(η)＞1.

（2）若M=0，则m=F(x2)＜0，由拉格朗日中值定理知，存在η2∈(x2,1)，使得

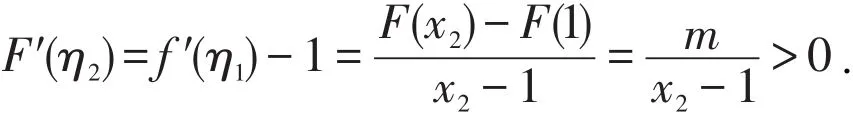
故 f′(η)＞1.

对于学生来说，这个证明还是有相当的技巧和难度.换句话说，如果只会证明，或者只看证明，很难帮助学生更好地理解问题本身.但是根据题意和已知的条件绘出图1，再结合导数的几何意义，结论是显而易见的.

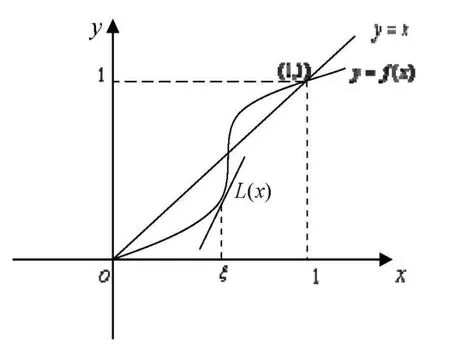
图1 曲线y=f(x)表示因变量y与自变量x之间的非线性关系，直线L(x)表示过曲线y=f(x)上的点ε的切线，其斜率大于1

更甚者，可以为其加上一个物理学背景.可将f(x)看成路程，变量x为时间，那么所研究的对象就变成“单位时间内路程为1（平均速度为1），但物体做非匀速直线运动，因此在某些时点上物体的速度绝对会超过平均速度1”这一问题了，由导数物理背景知，速度是路程函数的导数.这样的解释使题意与结论变得自然、直观且十分有趣.数学脱下了神奇而抽象的外衣，表现出可爱的一面——源于实际的数学，又奇妙地回归于实际.这样解决问题的方式，不仅使问题的背景、意义及其之间的关系变得清晰化，问题的解决过程不再云里雾里，还会让整个学习过程清爽愉快，学习效果明显提升.“理论联系实际”才是最符合高等数学教学的要求.

第三，为了达到上述要求，必须注意培养学生的图像能力，包括绘图能力和图像理解能力.总有一些学生的手工绘图能力较差，或者不善于将有关知识点与相应的图形特征联系起来.针对这一现状，教师在课堂讲授及习题讲解中可结合具体内容，一方面传授作图的基本技巧，如由简单函数的图像经叠加、压缩、旋转、对称及复合等变换生成各种较复杂的函数图像；另一方面利用图像特征进行辅助分析，由简单到复杂，由特殊至一般，逐步培养学生的图像基本功，培养学生把问题转化为图像的能力和利用图像分析并解决问题的能力.

3 高等数学在经济领域的应用

实践证明，用数学方法对经济问题做定性或者定量分析是十分有效的、可靠的.随着经济问题的多样化，在定量分析这些问题的时候，首先要根据经济理论，建立数学模型，然后通过分析数据，并运用概率统计方法对其结果进行分析，从而可以对于未来的经济状况作出预测，最终为决策者提供有效的决策信息.在上述过程中，每一步都与数学理论息息相关，比如在政策评价中，需要用到弹性函数、边际效用等，它们与高等数学中的微分学紧密相连.另外，在经济学和管理学中，最优化理论是极其重要的研究对象之一.通俗的来讲，就是在经济资源投入一定的前提下如何使效益达到最大；或者在效益一定的前提下如何使投入最小.现在举例说明：

例3 根据需求、收入及价格间的关系，假设某种商品在一定时期内的综合需求函数为D=0.5P-0.6X0.8，其中D为需求函数，P为该商品单位价格，X为人均月收入.由于该商品的需求富有弹性，即收入增加，需求增加；价格提高，需求下降.可见给出的函数关系是有意义的.

假设某地区人均月收入5000元，苹果手机的价格为4500元，则需求量为2.91.利用此结果，可为商家的进货量做出合理预测.同时，由需求函数可得：需求关于收入的偏弹性为，表明收入增加1%，对该商品的需求量增加0.8%.同理可得需求关于价格的偏弹性为αP=-0.6，也就是说当该商品价格提高1%，需求量下降0.6%.

例4 某公司有三条生产线生产两类产品，数据如表1，要求利润最大，该如何生产？

表1 公司的三条生产线生产不同类别产品的生产周期及其每天工作时间

解 设两类产品每天产量分别为x1,x2，每天利润为z，则x1,x2满足

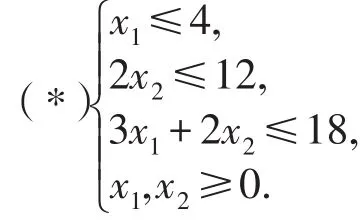
可行性域如图2.

故当x1=2,x2=6时，该公司的每天利润z=3x1+5x2达到最大.究其本质，该问题是利用线性规划理论求条件极值的问题，即在约束条件（*）下，如何才能实现目标函数z=3x1+5x2的最大值.由于约束条件中的函数及目标函数形式简单，也可以采取代入法，转换为无条件极值问题，结论相同.

图2 蓝色区域表示目标函数z=3x1+5x2在约束条件（*）下的可行性区域

4 总结

除上述几个方面外，“高等数学”教学中应该注意到的问题还有很多，比如习题讲解中“质”与“量”的关系问题，是追求大量讲解习题以帮助学生积累解题经验，还是少讲精讲而树立解题典型？又比如数学形式的严格性与讲授的通俗性的关系问题，若讲得通俗明白一点，学生容易接受，但可能牺牲数学科学的一部分严格性；若极力保持严格性，就不能太通俗，但学生很可能听不大懂.二者明显是不相容的，如何处理这个关系？有些问题难于定论，有待进一步的总结，继续探索教学规律.“高等数学”的教学方法可以不同，思想可以有所差别，然而有一点是明确无误的：我们的教学，务必想方设法地消除大多数学生对于数学课程的恐惧感，让他们喜欢数学、认识数学甚至学会鉴赏数学，并尽可能利用数学的思想和方法来指导他们的学习和日后的工作.

［1］齐民友.从微积分的发展看微积分的教学［J］.高等数学研究，2004，7（2）：2-6.

［2］鲍培文.例析数形结合思想在高等数学教学中的应用［J］.当代教育理论与实践，2012，4（10）：74-77.

［3］张莲.高等数学教学中极限的几种求法分析［J］.辽宁师专学院，2011，13（4）：15-15.

［4］杨丽贤，曹新成，关丽红.谈高等数学理论在经济领域的应用［J］.长春大学学报，2006，16（6）：20-22.

［5］同济大学数学系.高等数学［M］.6版.北京：高等教育出版社，2007.

Notes in the Teaching of Higher Mathematics

TANG Feng-qin，DU Cui-zhen
（School of Mathematical Sciences，Huaibei Normal University，235000，Huaibei，Anhui，China）

In this paper，three problems in the teaching of Higher Mathematics are presented，includ⁃ing the methods and thoughts of limit，the unity of quantity and graphic and the applications of high⁃er mathematics in economic area.Our discussions are devoted to improving the classroom teaching and arousing the students’interest in the higher mathematics.

higher mathematics；limit；unity of quantity and graphic

O 13

C

2095-0691（2015）01-0082-05

2014-07-10

淮北师范大学教学研究项目（jy13231）

唐风琴（1983- ），女，江苏连云港人，讲师，研究方向：概率论极限理论.