有阻尼吸振器参数优化与应用
王卫峰,丁智平,贺才春,涂奉臣,穆龙海
(1.湖南工业大学 机械工程学院,湖南 株洲 412007;2. 株洲时代新材料科技股份有限公司,湖南 株洲 412007)
有阻尼吸振器参数优化与应用
王卫峰1,2,丁智平1,贺才春2,涂奉臣2,穆龙海1
(1.湖南工业大学 机械工程学院,湖南 株洲 412007;2. 株洲时代新材料科技股份有限公司,湖南 株洲 412007)
针对某一特定频率下的振动问题,优化有阻尼吸振器参数来对其进行吸振。先对悬臂梁进行模态分析,得到对振动贡献最大的频率并确定吸振器的安装位置;然后,应用单自由度质量感应法得到动力吸振器在主振动系统上安装位置点的等价质量和等价刚度,并由其组成一个等效的单自由度系统;建立吸振器的数学模型,并基于理论推导出具有单自由度的动力吸振器的解析解,得到吸振器的3个参数;以悬臂梁为例,应用Abaqus软件仿真附加吸振器前后测试点的振动响应。仿真结果显示,安装动力吸振器后,测试点的振动得到显著降低,证实了吸振器的有效性。
动力吸振器;悬臂梁;质量感应法;Abaqus软件
0 引言
振动广泛存在于人们的日常生产生活中。工程设计人员应用振动原理制造了许多机械设备,如振动筛、振动沉桩机等。同时,振动也带来了负面影响,使机械设备受到疲劳损坏,缩短其工作寿命,还造成严重的噪声污染[1]。为了控制机械设备的振动在允许范围内,保证机械正常运转和操作人员的人身安全,学者们提出了振动控制技术[2-3]。动力吸振器(dynamic vibration absorber,DVA)是一种经济、有效的减振方法,可以在一定频率范围内减小被吸振结构的振动响应[2]。
国内外学者对动力吸振器都有深入的研究,在工程上也有许多的应用实例[4-7]。悬臂梁的振动现象在机械设备中广泛存在,并且时常会在某个频率下出现异常振动问题。针对这类振动问题,本文以梁的一阶振动问题为例,对动力吸振器的设计及应用方法进行了研究,并应用仿真技术验证了所设计的动力吸振器的有效性。
1 有阻尼动力吸振器的工作原理
动力吸振器技术在船舶[8]、铁路、航空[9]、电力、建筑、车辆[10]等领域都有着广泛的应用。其工作原理是,在主系统上附加具有质量弹簧的子系统,附加系统在共振时会产生反作用力,使振动所产生的能量由主系统转移至吸振器,从而减少或抑制主系统受外激励时的响应[6]。
本文将主系统简化为单自由度系统,其质量、刚度由质量感应法得到对应的等效值,动力吸振器采用有阻尼动力吸振器。有阻尼动力吸振器是由质量、刚度、阻尼3个元素组成,通过3个参数的最优组合使得主系统在受外激励时的振动响应达到最小,其力学模型如图1所示。
图中参数说明如下:
m1, m2分别为主系统和动力吸振器的质量;
x1, x2分别为主系统和动力吸振器的位移;
k1, k2分别为主系统和动力吸振器的刚度;
c为动力吸振器的阻尼;

图1 有阻尼动力吸振器的力学模型图Fig. 1 Mechanical model diagram of damped dynamic vibration absorber
主系统受到外力激励时,系统的运动微分方程为[2]:


针对特定频率的减振,安装和未安装动力吸振器时,主系统的频率响应曲线如图2所示。由图可知,加装吸振器后主系统的减振效果显著[11]。
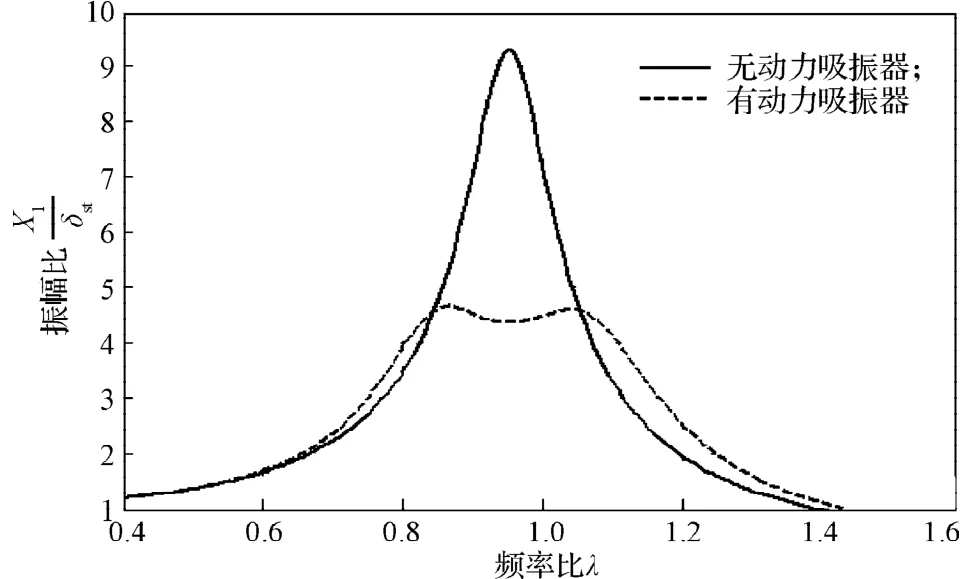
图2 安装和未安装动力吸振器时主系统的频率响应曲线图Fig. 2 The frequency response curve of the primary system with and without dynamic absorber
2 定点理论的参数优化
定点理论是指对于含有制振器阻尼的振动系统,利用频率响应函数曲线上与阻尼无关的特定点来设计制振装置的方法[2]。
相同质量比条件下,三要素DVA具有比Voigt式DVA更好的减振效果。 学者们还推导出三要素DVA的最优设计公式。
满足最优同调条件的动力吸振器与主振动系统的固有频率比为

满足动力吸振器的最优阻尼比为
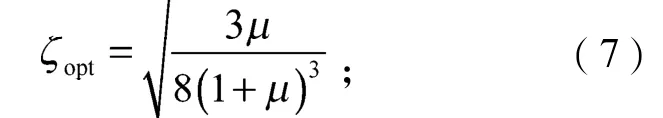
满足最优条件时的最大振幅比为

图3为定点与满足最优条件的振幅比曲线关系图。由图可知,在质量比(=0.1)和固有频率比不变的前提下,当改变结构阻尼比时,其振幅比曲线都会经过2点P, Q,这就是所谓的2个定点。在最优同调和最优阻尼的组合下,P,Q 2点不仅仅是整条曲线中值最大的点,而且2点也是等高的。

图3 定点与满足最优条件的振幅比曲线关系图Fig. 3 The relationship curve of the fixed point and amplitude ratio under optimal condition
3 设计案例——梁的应用
为了验证动力吸振器的吸振效果,对悬臂梁进行模态分析,得到其各阶的固有频率及其对应的振型。本文仅以悬臂梁第一阶固有频率作为吸振频率,并在这一频率的最大振幅位置上安装动力吸振器,以为观察目标,分析安装动力吸振器前后的制振效果。
3.1 悬臂梁模型及有限元模态分析
本文应用Abaqus软件建立尺寸400 mm×40 mm× 5 mm的悬臂梁模型,材料为铸钢。材料的物理性能为:密度=7.8 g/cm3,弹性模量E=2.1×105MPa,泊松比=0.3,结构阻尼比=0.01。将悬臂梁的左端进行全约束,x轴作为梁的长度方向,y轴作为梁的宽度方向,轴作为厚度方向。悬臂梁模型用一个赋予了厚度的平面来表示,并且将平面划分为40×6的长方形单元。
在Abaqus软件中,首先对悬臂梁进行模态分析,提取其前十阶的固有频率,分别为26.34, 165.09, 205.38, 462.85, 493.80, 909.17, 1 236.00, 1 489.10, 1 507.80, 2 261.20 Hz。对于连续性主系统,若其各阶固有频率相隔较远时,则可以忽略各个模态间的相互影响,因此,在振动控制时,可以将各个模态分别进行处理[2]。通过有限元分析可知,悬臂梁的第一阶模态振型主要是集中在 轴方向,在 轴方向上的最大位置为节点154。通常,吸振器安装在振幅最大位置时,吸振效果最佳,因此文中选择悬臂梁的第一阶固有频率f=26.34 Hz作为吸振频率,其振型在 轴方向的最大位置为动力吸振器的安装位置。

图4 固有频率26.34 Hz所对应的振型图Fig. 4 Natural frequency of 26.34 Hz corresponding the vibration mode
为了比较附加动力吸振器前后,其观察目标关于频率的变化值,并且考虑到悬臂梁的第一阶模态振型主要是集中在 轴方向,本文在主系统自由端的一个节点上沿 轴方向施加了一个单位载荷的简谐激励,这样便能激励出该阶的振型。这里所取的频率变化范围为10~200 Hz。
3.2 附加质量法得到等效质量
质量感应法是普遍使用的一种方法。其原理是在动力吸振器或作动器的设置位置附加一个给定的质量,再根据附加质量前后对象结构固有频率的变化来得到主结构的等价质量[12-13]。由于是基于单自由度系统的假定而确立的方法,因而称之为单自由度质量感应法。
主系统的等价质量m和等价刚度k的计算式为:
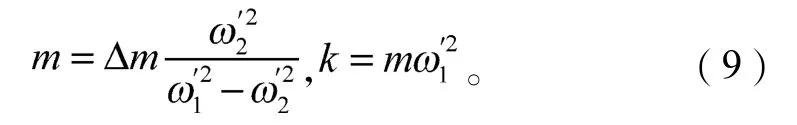
式中:Δm为附加的给定质量;
由于本文将动力吸振器安装于第一阶固有频率
23.64 Hz的最大振幅处,因此,在该点附加一个0.06 kg的质量块。由式(9)可以得到等价质量m=0.15 kg,等价刚度k=4 221 N/m。
3.3 动力吸振器参数设计
根据动力吸振器相关理论,质量比越大,系统的吸振效果越好,吸振的频带也越宽。已有文献证明当设定的质量比大于0.1时,若再增加附加吸振器的质量,则其减振效果提高很缓慢,并且质量比的增大会导致所附加的动力吸振器的质量增大,从而使得总体的安装布置变得困难[6-7],故设定吸振器的质量比为0.1。
悬臂梁第一阶弯曲的模态固有频率为26.34 Hz,由质量感应法得到主系统的等价质量为0.15 kg,质量比=0.1,将其代入式(6)和式(7)中,可得动力吸振器的质量为0.015 kg,刚度为348.8 N/m,阻尼为0.86 (N·s)/m。
3.4 吸振效果分析
应用Abaqus软件对动力吸振器进行模态分析。先建立等效的单自由度模型,输入各参数数值,最后计算其模态。由仿真分析可知,动力吸振器的固有频率为23.54 Hz,阻尼比为0.19。
将所设计的动力吸振器安装到悬臂梁的相应位置,对其效果进行模拟验证。图5为装入吸振器后的模型。对悬臂梁的左端进行了全约束,在参考点RP-1上建立了一个等效吸振器的质量点,并将其与节点154用弹簧和阻尼连接模拟动力吸振器。同时,在节点154施加了单位间谐激励载荷。

图5交互界面图Fig. 5 Interaction interface
图6 为安装动力吸振器前后在节点154上的振动幅度响应曲线图。由图可知,振动在26.34 Hz处得到了抑制,同时原主峰值的两侧出现了2个矮峰,2条曲线的交点处横坐标值分别为21.28, 30.16 Hz,即此动力吸振器的有效宽带为8.80 Hz。振动的位移衰减在90%以上,其吸振效果十分明显。
由仿真结果可知,根据理论所设计的动力吸振器能够有效地抑制悬臂梁第一阶固有频率的振动,并且其有效带宽较宽。
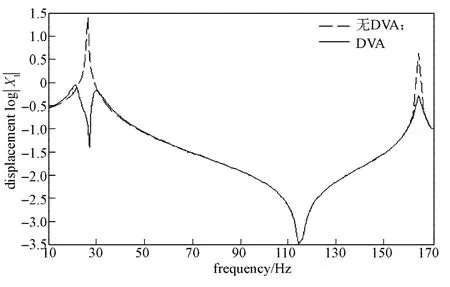
图6 安装动力吸振器前后节点154的振幅图Fig. 6 The amplitude of node 154 before and after installation of vibration absorber
4 结语
文对有阻尼动力吸振器的基本原理进行研究。以悬臂梁为例,先利用Abaqus软件建立其模型,并进行有限元模态分析;然后,针对悬臂梁模型的第一阶固有频率,应用质量感应法得到了吸振器安装位置上的等价质量和等价刚度,为动力吸振器参数的设计提供有力的支撑;最后优化有阻尼动力吸振器的参数,仿真分析在悬臂梁节点154上安装动力吸振器后的吸振效果。仿真结果表明,该动力吸振器的吸振效果良好。
[1]陈建国,夏 禾,曹艳梅,等. 运行列车对周围建筑物振动影响的试验研究[J]. 振动工程学报,2008,21(5):476-481. Chen Jianguo,Xia He,Cao Yanmei,et al. Experiment on Running Train Induced Vibrations of Nearby Buildings[J]. Journal of Vibration Engineering,2008,21(5):476-481.
[2]背户一登. 动力吸振器及其应用[M]. 北京:机械工业出版社,2013:78-79. Beihu Yideng. Dynamic Vibration Absorber and Its Application[M]. Beijing:China Machine Press,2013:78-79.
[3]刘耀宗,郁殿龙,赵宏刚,等. 被动式动力吸振技术研究进展[J]. 机械工程学报,2007,43(3):14-21. Liu Yaozong,Yu Dianlong,Zhao Honggang,et al. Review of Passive Dynamic Vibration Absorbers[J]. Chinese Journal of Mechanical Engineering,2007,43(3):14-21.
[4]Son Y K,Savage G J. Optimal Probabilistic Design of the Dynamic Performance of a Vibration Absorber[J]. Journal of Sound and Vibration,2007,307(1):20-37.
[5]李 勇,顾 彦,靳春梅. 汽车动力吸振器优化设计[J].噪声与振动控制,2011,31(6):123-126.Li Yong,Gu Yan,Jin Chunmei. Optimal Design of Automobile’s Vibration Absorber[J]. Noise and Vibration Control,2011,31(6):123-126.
[6]魏榕祥,陈国平,黄瑞泉,等. 动力吸振器抑制某型飞机平尾振动的设计与试验研究[J]. 南京航空航天大学学报,2012,42(3):307-312. Wei Rongxiang,Chen Guoping,Huang Ruiquan,et al. Design and Experiments of Dynamic Absorber for Aircraft Tailplane[J]. Journal of Nanjing University of Aeronautics & Astronautics,2012,42(3):307-312.
[7]陶 杰,吴坚华,刘德立. 船艉结构动力吸振器的试验研究[J]. 振动与冲击,1997,16(1):80-83. Tao Jie,Wu Jianhua,Liu Deli. Application of Modal Analysis in Parameter Optimization of Dynamic Vibration Absorber[J]. Journal of Vibration and Shock,1997,16(1):80-83.
[8]郭有松,李 超,王德禹,等. 军用船舶动力吸振器性能与参数优化研究[J]. 舰船科学技术,2014,36(7):48-52. Guo Yousong,Li Chao,Wang Deyu,et al. Parameter and Performance Research of Dynamic Vibration Absorber Applied in Marine Vessels[J]. Ship Science and Technology,2014,36(7):48-52.
[9]周 薇,韩景龙. 直升机桨叶/吸振器系统的组合共振研究[J]. 振动工程学报,2015,28(2):248-254. Zhou Wei,Han Jinglong. Helicopter Blade-Absorber System Combination Resonance Research[J]. Journal of Vibration Engineering,2015,28(2):248-254.
[10]赵 悦,肖新标,韩 建,等. 高速有砟轨道钢轨动力吸振器垂向吸振特性及其参数影响[J]. 机械工程学报,2013,49(16):17-25. Zhao Yue ,Xiao Xinbiao,Han Jian,et al. Vertical Characteristic and Its Parameter Effect of Rail Vibration Absorber used in High-Speed Ballasted Track[J]. Chinese Journal of Mechanical Engineering,2013,49(16):17-25.
[11]李剑锋,龚兴龙,张先舟,等. 主动移频式动力吸振器及其动力特性的研究[J]. 实验力学,2005,20(4):507-514. Li Jianfeng,Gong Xinglong,Zhang Xianzhou,et al. Study of Adaptive Tuned Vibration Absorber and Its Dynamic Properties[J]. Journal of Experimental Mechanics,2005,20(4):507-514.
[12]Seto K,Ookuma M,Yamashita S,et al. Method of Estimating Equivalent Mass of Multi-Degree-of-Freedom System[J]. Bulletin of the JSME,1987,30(268):1638-1644.
[13]宋 波,刘浩鹏,张国明. 基于附加质量法的桥墩地震动水压力分析与实例研究[J]. 土木工程学报,2010,43 (增刊1):102-107. Song Bo,Liu Haopeng,Zhang Guoming. Analysis and Case Study of Earthquake Induced Hydrodynamic Pressure on Deep Water Bridge Based on Added Masses Approach[J]. China Civil Engineering Journal,2010,43(S1):102-107.
(责任编辑:邓 彬)
The Parameter Optimization and Application of Damping Absorber
Wang Weifeng1,2,Ding Zhiping1,He Caichun2,Tu Fengchen2,Mu Longhai1
(1. School of Mechanical Engineering,Hunan University of Technology,Zhuzhou Hunan 412007,China;2. Zhuzhou Time New Material Technology Co., Ltd.,Zhuzhou Hunan 412007,China)
Aimed at vibration problems of a particular frequency, optimizes the parameters of the damping vibration absorber for the vibration absorption. Analyzed the cantilever beam modal, obtained the frequency of maximum contribution to vibration and determined the installation position of absorber; Applied the single free induction method to obtain equivalent mass and equivalent stiffness of dynamic vibration absorber on main vibration system installation position and built an equivalent single degree freedom system; Established the absorber mathematical model, and deduced theoretically the analytical solution for a single degree dynamic absorber and obtained three parameters for the absorber. Taking the cantilever beam as an example, applied Abaqus software to simulate the vibration response of test points attached to the vibration absorber front and back. The results showed that the vibration of test points was greatly decreased and the effectiveness of absorber was verified.
dynamic vibration absorber;cantilever beam;quality induction method;Abaqus software
TB123
A
1673-9833(2015)05-0040-05
10.3969/j.issn.1673-9833.2015.05.009
2015-07-22
王卫峰(1990-),男,湖南衡阳人,湖南工业大学硕士生,主要研究方向为机械结构强度理论,E-mail:friendswwf@163.com

