一类具有时滞和放养的扩散系统的周期解

王晖

（内蒙古民族大学 数学学院，内蒙古 通辽 028000）

一类具有时滞和放养的扩散系统的周期解

王晖

（内蒙古民族大学 数学学院，内蒙古 通辽 028000）

研究一类具有Beddington功能反应和放养的Lotka-Volterra 扩散系统。证明了系统正周期解的存在性，并通过构造适当的Lyapunov泛函，给出了正周期解全局稳定的充分条件。

时滞；扩散；放养；正周期解；全局稳定性

1 研究背景

国内外很多学者对具有功能反应的捕食周期系统进行了大量研究[1-8]。如：文献[6]研究了时标上具有阶段结构的三种群捕食系统。运用时标上连续拓扑度定理，得到了系统存在周期解的充分条件，其研究方法使系统的连续时间情形和离散时间情形的周期解问题得到了统一。文献[7]研究了一类具有保护区和避难所效应的捕食系统周期解存在性。利用重合度理论，得到系统至少存在8个正周期解的充分条件,并举例子说明了结果的有效性。由于环境的变化、人为的干预或外来物的影响，都不同程度地影响着生物的持续生存和灭绝，于是越来越多的现实因素被考虑到模型中来。不论是野生的还是人工饲养的种群，人们常采取扩散和放养（食饵补充）来加以保护或控制。特别是当捕食者种类多、密度大或捕食能力强时，常通过补充食饵使种群的数量趋于稳定，以达到生态平衡。

文献[8]研究了具有扩散和放养的两种群竞争系统，得到了系统周期解的存在性，唯一性和全局渐近稳定性的充分条件，但文献[8]研究的种群比较少，且没有给出捕食者种群的捕食率，而生态系统中多见的是多种群相继捕食的生物链。因此，本文在文献[8]的基础上考虑了捕食率为Beddington型功能反应的三种群相继捕食的扩散模型，即如下模型：

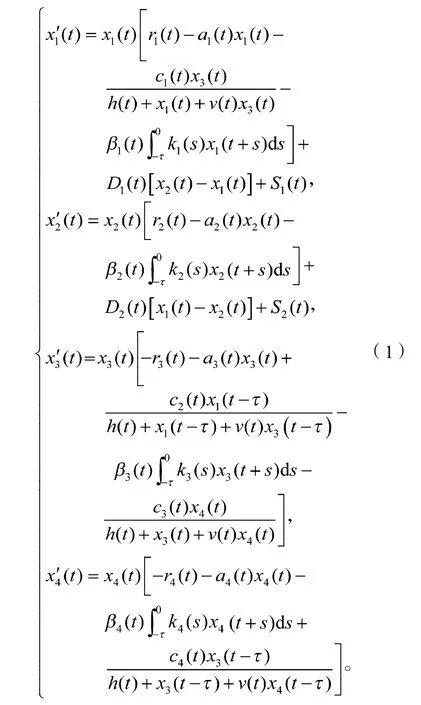
式中：xi(t)(i=1, 2, 3, 4)分别为被捕食种群和捕食者种群的密度，x1(t), x2(t)分别为被捕食种群在斑块Ⅰ和Ⅱ中的密度，而捕食者种群被限制在斑块中不能扩散；

x3(t)以x1(t)为食，x4(t)以x3(t)为食，如此相继捕食，形成了一个生物食物链；

Di(t)(i=1, 2)，Si(t)(i=1, 2)分别为被捕食种群在斑块Ⅰ或Ⅱ中的扩散率和投放率，

ri(t), ai(t), ci(t),i(t) (i=1, 2, 3, 4)均为模型的系数；

ki(s)（i=1, 2, 3, 4）, v(t), h(t)均表示函数。

2 基本概念和假设

3 解的正性

4 周期解的持久性

由定义1和引理2可得如下定理：

定理1 如果模型（1）满足条件H1～H7，则模型（1）是一致持久的。

5 周期解的唯一性和全局稳定性

定理2 假设在H1～H7下，还有：

因此，模型（1）的周期解是唯一的且是全局稳定的。

[1]Xu R，Chaplain M A J，Davidson F A. Periodic Solution of a Lotka-Volterra Predator-Prey Model with Dispersion and Time Delays[J]. Appl. Math. Comput.，2004，148 (2)：537-560.

[2]Song Xinyu，Chen Lansun. Persistence and Global Stability for Nonautonomous Predator Prey System with Diffusion and Time Delay[J]. Computers Math. Applic.，1998，35 (6)：33-40.

[3]Chen Fengde，Shi Jinlin，Chen Xiaoxing.A Nonautonomous Diffusion Predator-Prey System with Functional Response and Time Delay[J]. Pure and Applide Mathematics，2003，19(4)：311-317.

[4]Wang Hailing，Zhong Shouming，Tian Baodan. Permanence and Existence of Periodic Solutions of a Predator-Prey Patchy Model with Dispersal and Time Delay[J]. Math. Biosci.，2007，22(1)：25-36.

[5]Dong Ranran，Zhang Daoxiang，Yin Hongyun. Periodic Solutions for a Ratio-Dependent Three-Species Predator-Prey Diffusion System with the Beddington-DeAngelis Functional Response[J]. Journal of Biomathematics，2012，27(2)：213-223.

[6]徐昌进. 时标上具有阶段结构的三种群捕食系统的周期解[J]. 经济数学学报，2013，30(1)：5-11. Xu Changjin. Periodic Solutions for a Three Species Predator-Prey System with Stage-Structure on Time Scales[J]. Journal of Quantitative Economics，2013，30(1)：5-11.

[7]贾素娟，魏凤英. 具有保护区和避难所效应的捕食系统周期解的存在性[J]. 福州大学学报：自然科学版，2012，40(4)：423-428. Jia Sujuan，Wei Fengying. Existence of Solutions to Predator-Prey Systems with Protected Areas and Refuges [J]. Journal of Fuzhou University：Natural Science Edition，2012，40(4)：423-428.

[8]陈福来，文贤章. 具有扩散和放养的时滞竞争系统的正周期解[J]. 生物数学学报，2006，21(1)：57-67. Chen Fulai，Wen Xianzhang. Positive Periodic Solution for Delay Competition System with Diffusion and Stock[J]. Journal of Biomathematics，2006，21(1)：57-67.

[9]Barbalat I. Systems D’equations Differentielle D’oscillations Nonlinraires[J]. Rev. Roumaine Math. Pures Appl.，1959，4：267-270.

（责任编辑：邓光辉）

The Periodic Solutions of Diffusion System with Stock and Time Delay

Wang Hui
（Mathematics College，Inner Mongolia University for the Nationalities，Tongliao Inner Mongolia 028000，China）

Researches a Lotka-Volterra diffusion system with Beddington function response and stock. Proves the existence of positive periodic solution for the system, and by constructing appropriate Lyapunov function, provides sufficient conditions for the global stability of positive periodic solution.

time delay；diffusion；stock；positive periodic solution；global stability

O175.13

A

1673-9833(2015)03-0094-07

10.3969/j.issn.1673-9833.2015.03.018

2015-04-04

内蒙古自治区高等学校教学改革研究基金资助项目（2013NMJG032），内蒙古民族大学教育教学研究基金资助项目（MDYB201406）

王 晖（1982-），女，四川德阳人，内蒙古民族大学讲师，硕士，主要研究方向为生物数学，E-mail：whll_clam@163.com