基于熵权法的高校体育教师评价指标体系的建立

毛毅钢

(渤海大学体育教研部，辽宁锦州 121013)

教师是提高教育质量的关键因素，是推进教育变革的核心力量，建设具有良好政治业务素质、结构合理、相对稳定的教师队伍，是教育改革和发展的根本大计。提高全民族素质，实现科教兴国战略，必须提高教师水平。体育教育是实施全面素质教育的重要内容之一，要使学生得到“德、智、体、美、劳”等素质的全面发展，就要充分发挥体育教育在素质教育中的作用［1］。体育教师评价作为教师评价的有机组成部分，对其评价体系的建立始终是一个薄弱环节，缺少系统有效的理论指导和技术支撑，随着高等教育改革以及素质教育的不断深入，产生的弊端日益显现，制约了高校体育教育工作的开展［2］。构建高校体育教师综合素质评价指标体系，有助于确立体育教师评价的价值取向和明确体育教师评价的目标，制定适合体育教师专业特点的评价方案，采用先进的教师评价理念和科学的态度指导体育教师评价的实践活动，促进体育教师素质的不断提高和专业的持续发展，提高学校体育教育教学工作质量，为全面提高学生的综合素质打下坚实的基础。

1 评价指标体系结构模型

评价指标体系的建立是评价工作正确进行的基础，测量与评价的可靠性，在很大程度上取决于所设计指标的有效程度。建立合理可靠的分析评价模型，必须首先建立有效的评价指标体系［3］。本文综合运用文献资料法、专家访谈法、问卷调查法、数据统计法等多种方法［4］，并遵循方向性与主体性相结合、科学性与可行性相结合、静态性与动态性相结合、奖惩性与发展性相结合、定性与定量相结合等原则，结合体育教学的特点，综合考虑教学、科研、知识、素质等因素，在参照前人研究成果的基础上，构建了由职业思想道德、教学方案设计、教学过程实施、专业技术素质、学识知识水平、业余运动训练、科学研究探索、职业创新发展、社会服务指导、信息技术应用、组织协调管理、团队沟通合作等指标构成的评价指标体系，结构模型如图1所示。

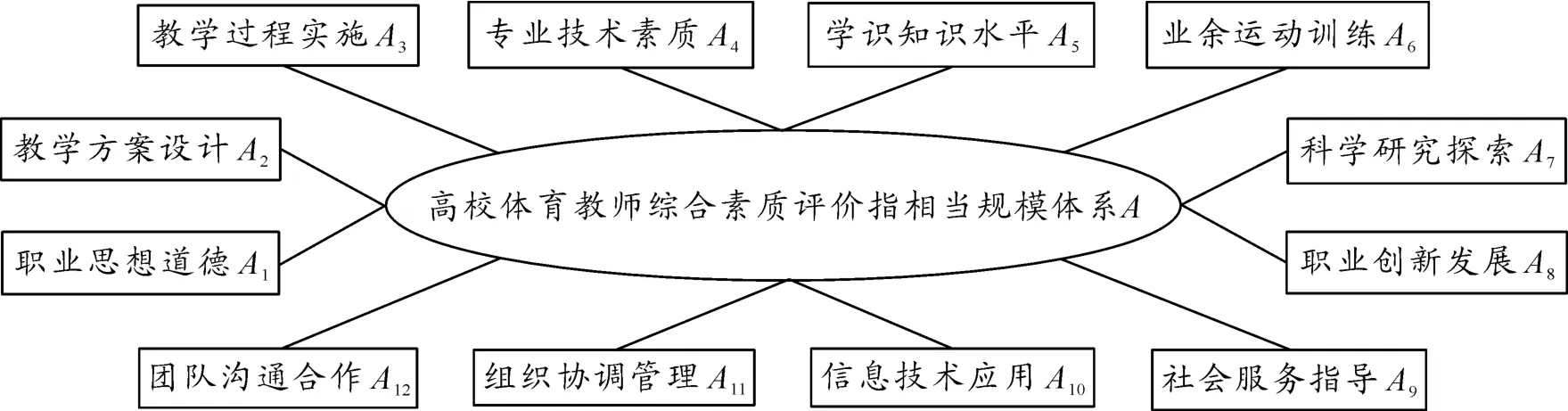
图1 高校体育教师综合素质评价指标体系结构模型

2 熵权法计算权重数学模型

权重是否合理直接影响到评价的科学性。权重是指某一指标在整体度量中的相对重要程度，一组度量指标体系相对应的权重组成了权重体系［5］。计算权重的方法有很多，本文选用熵权法。

熵权法(entropy-right method，ERM)的基本原理是通过度量评价指标体系中指标数据所蕴含的信息量来计算各指标的权重。当评价对象在某项指标上的值相差较大时，熵值较小，说明该指标提供的有效信息量较大，指标的权重也应较大;反之，若某项指标的值相差越小，熵值较大，说明该指标提供的信息量较小，指标的权重也应较小［6］。

2.1 熵的定义及其性质

熵(entropy)，在物理学上指热能除以温度所得的商，标志热量转化为功的程度;科学技术上用来描述、表征体系混乱度的函数，亦被社会科学用以借喻人类社会某些状态的程度。

设系统可能会处于如下n种不同状态:S1，S2，…，Sn。令 i=1，2，…，n，则系统处于 Si的概率为［7］:

如果上式中 Pi(i=1，2，…，n)的值已知，则系统熵的计算公式为:

其中:0≤Pi≤1，∑Pi=1。

熵具有以下数学性质［8－9］:

1)对称性。设n个事件的概率分布为p1，p2，…pn，当事件的位置顺序任意调换后得到新的概率分布为 p'1，p'2，…p'n，有下式成立:

2)非负性。H(p1，p2，…pn)≥0。因为 pi≤1，所以 lnpi＜0，可得－lnpi＞0。

3)确定性。信源中只要有一个事件的概率是1，则其他事件的概率是0，即:

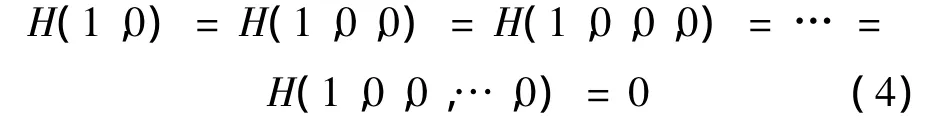
4)可加性。对于2个随机变量 X和Y，H(XY)为2个变量的联合熵，H(XY)等于X的无条件熵加上已知X时Y的条件概率的熵的平均值，即:

5)极值性。当系统状态为等概率，即，Pi=，i=1，2，…，n 时，熵最大，有:

当系统状态任意时，有:

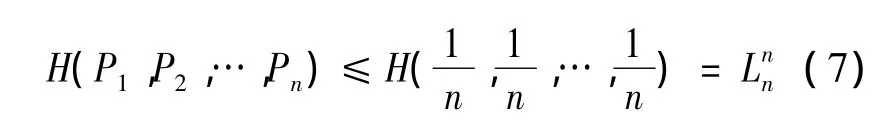
6)扩展性。对于2个集合X和Y，若集合X有n个事件，集合Y有n+1个事件，但集合Y仅比集合X多一个概率近似于0的事件时，则2个集合的熵值相等，即:

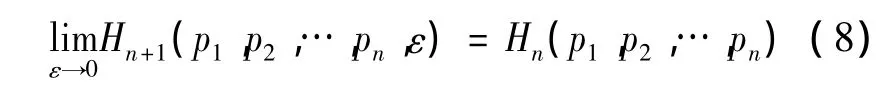
上式表明:当一个事件的概率和集合中其他事件的概念相比较小时，它对集合中熵值的贡献可以忽略不计。

2.2 熵权法计算权重步骤

熵权法计算权重分为5步:

1)单指标评价。单指标评价即对一个被评价对象的一个评价指标进行评价，可以采用历史数据法、专家打分法、综合统计法、排序综合法等一种方法或几种方法的组合。设有m个被评价对象，n 个评价指标，xij表示第 i(i=1，2，…，m)个被评价对象的第j(j=1，2，…，n)个评价指标的评价值，所有被评价对象的单指标评价结果构成m×n阶评价矩阵 Sm×n。

2)数据的归一化［10］。数据的归一化的目的是将不同量纲和不同数量级大小的数据转变成可以相互进行数学运算的具有相同量纲和相同数量级的具有可比性的数据。对于样本数据xi(i=1，2，…，m)，可采用最大最小值法、均值法和中间值法等归一化方法。本文使用最大最小值法，将样本数据归一化到［0，1］范围内，归一化后构成的矩阵为 Tm×n=［yij］m×n，单一指标归一化公式为:

3)计算指标值比重。计算结果构成的矩阵为 Um×n=［uij］m×n，第 i个被评价对象的第 j个评价指标值比重uij的计算公式为:

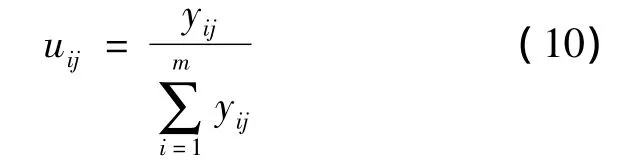
4)计算指标熵值。先进行预处理，得到Vm×n=［vij］m×n矩阵，vij的计算公式为:

指标熵值计算结果为 En=［e1，e2，…，en］，单一指标ej的计算公式为:

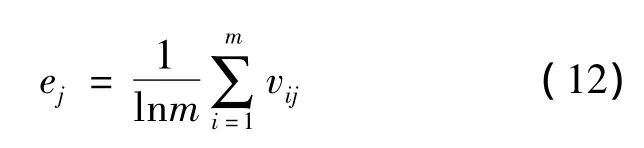
5)计算指标熵权。所有指标熵权计算结果为 Wn=［w1，w2，…，wn］，单一指标 wj的计算公式为:

3 指标体系权重计算过程与结果

某高校体育教研室有7名高级职称教师，现聘请10位专家对这7名教师的12项指标分别打分，根据专家打分结果计算指标权重。

1)单指标评价。单指标评价采用算术平均法构成的S7×12评价矩阵如下:

2)数据的归一化。对S7×12矩阵运用式(9)计算结果如下:

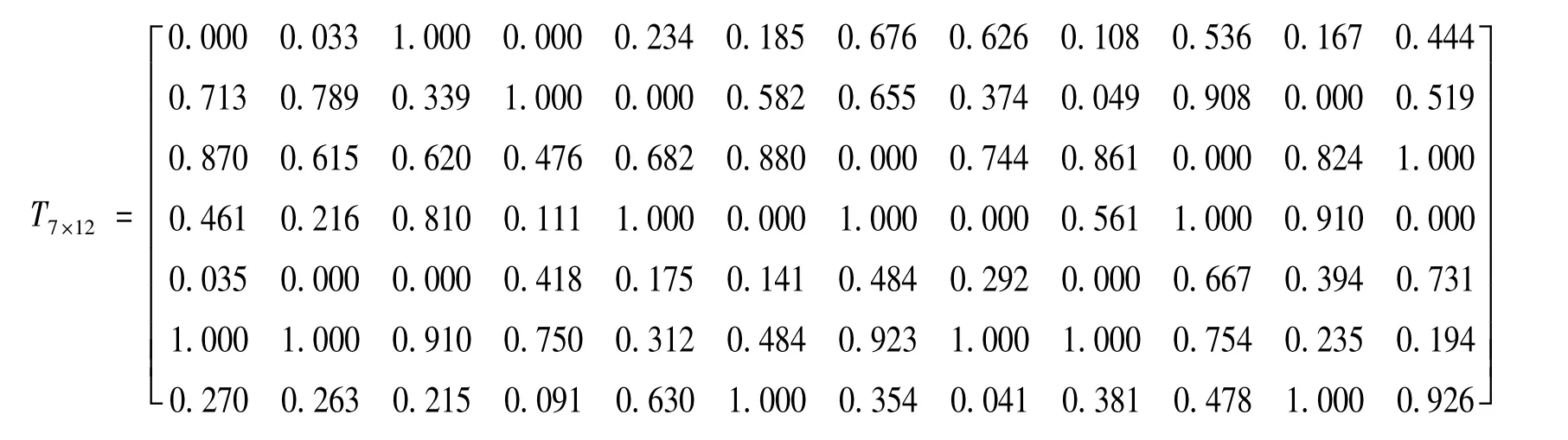
3)计算指标值比重。对T7×12矩阵运用式(10)计算结果如下:

4)计算指标熵值。为U7×12矩阵运用式(11)进行预处理结果如下:

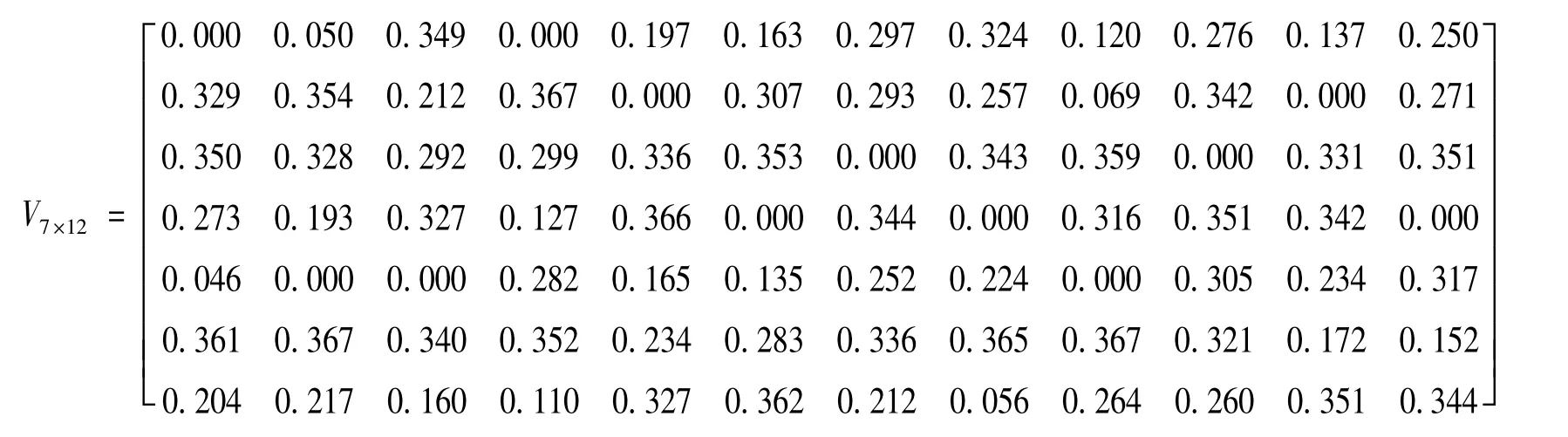
运用式(12)计算的指标熵值结果矩阵如下:

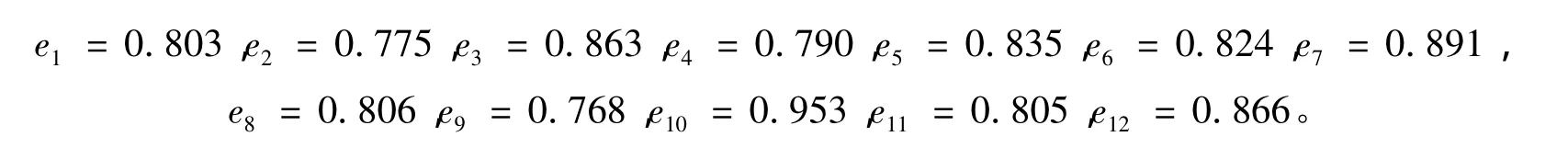
计算结果构成的指标熵值矩阵为:

5)计算指标熵权。运用式(13)计算结果如下:

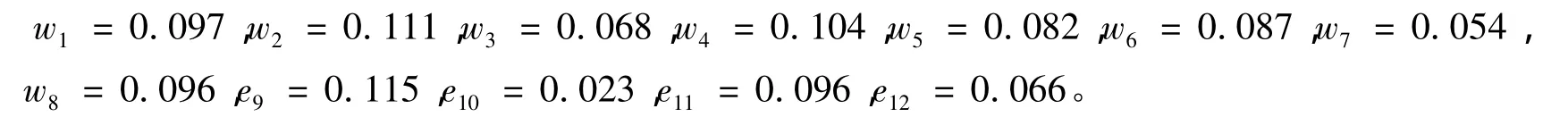
计算结果构成的指标权重矩阵为:

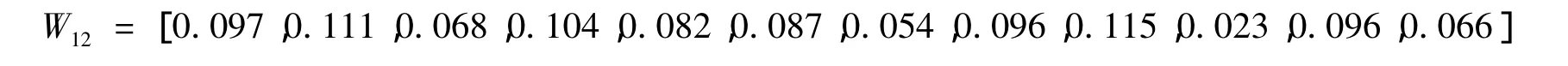
4 结束语

有效地开展教师评价，对于全面贯彻党的教育方针、不断深化教育教学改革、加强教师队伍管理、促进教师专业发展、提高学校教育质量和培养社会需求的合格人才等方向具有重要作用。本文针对高校体育教师的特点，确定了评价指标体系结构模型，用熵权法计算了指标体系权重。熵权法是一种在综合考虑各指标提供信息量的基础上计算权重的数学方法，根据指标变异程度，利用信息熵计算指标熵权，再通过熵权对各指标的权重进行修正，从而得出较为客观的指标权重。因此，本文计算的指标权重，具有较强的科学性和可操作性，符合测量学的要求。实际应用时要注重单指标评价，并与多种方法相结合，使权重值更客观实际。

［1］陈果.论体育在素质教育中的地位与作用［J］.教育教学论坛，2012，5(7):13－14.

［2］曾庆涛.我国体育教师评价体系研究［D］.郑州:河南大学，2011.

［3］卓建南，尹少丰.普通高校体育教师教学能力量化评价研究［J］.安徽师范大学学报:自然科学版，2008，31(6):609－612.

［4］陈秀云，周新业.全国普通高校体育教师评价体系研究［J］.广州体育学院学报，2010，30(3):96－100.

［5］王莉军.高等院校科技创新能力模糊聚类分析［J］.渤海大学学报:自然科学版，2013，34(2):220－224.

［6］邹志红，孙靖南，任广平.模糊评价因子的熵权法赋权及其在水质评价中的应用［J］.环境科学学报，2005，25(4):552－556.

［7］赵冬梅，张玉清，马建峰.嫡权系数法应用于网络安全的模糊风险评估［J］.计算机工程，2004，30(18):21－23.

［8］Héctor A M，López-Torres G C，Laura R R.Developing a Method to Evaluate Entropy in Organizational Systems［J］.Procedia Computer Science，2014，28(1):389－397.

［9］Giagkiozis I，Purshouse R C，Fleming P J.Generalized decomposition and cross entropy methods for many-objective optimization ［J］.Information Sciences，2014，282(20):363－387.

［10］百度文库，数据预处理之归一化［EB/OL］.［2014－09－05］.http://wenku.baidu.com/link?url=lVXCX_0FJ26YEiJ4R28AmsUgnjA0mWclBLYGXcBZh6QpQ01N oy5guxyBHxybpqqlla-IRHrI－81usc4EzXAw3A4DgR7qN bRVQHzCcAC.