CCR—DEA模型中弱有效决策单元对效率值的影响分析

彭宜青，姚晓闺，王 磊

(解放军陆军军官学院，合肥 230031)

数据包络分析方法(data envelopment analysis，DEA)是一种用来评价决策单元(DMU)之间相对有效性的方法。它以待评价系统的投入、产出指标的权系数为优化变量，运用数学规划模型，对待评价系统的相对有效性做出评价，因此对某个DMU有效性评价的结果依赖于其他的DMU。当增加新的DMU到原有的DMU集中或者从原有的DMU集中减去某些 DMU时，可能会对其余的DMU效率值产生影响，同时在对新加入的DMU进行有效性判断时，一般是与DMU集中所有元素进行比较判断，计算量也较大。文献［1－3］中指出:当判断决策单元集中的某一个DMUj效率值时，非有效的DMU对DMUj效率值不产生影响，只有其中的有效DMU会对DMUj产生影响。而有效DMU也可分为几种类型，文献［1］并没有指出不同类型的有效DMU会对DMUj的效率值产生何种影响。本文在此基础上讨论了弱有效DMU会对DMUj的效率值产生的影响。

1 DEA基本理论

假设决策单元集中有n个DMUs，DMUj(1≤j≤n)的输入、输出向量分别为 xj=(x1j，x2j，…，xmj)T＞0，yj=(y1j，y2j，…，ysj)T＞0，j=1，2，…，n。评价DMUj0DEA有效性的最初CCR模型为一个分式规划，利用Charnes-Coope变换，可化为一个等价的线性规划，引入松弛变量后可得以下对偶规划:

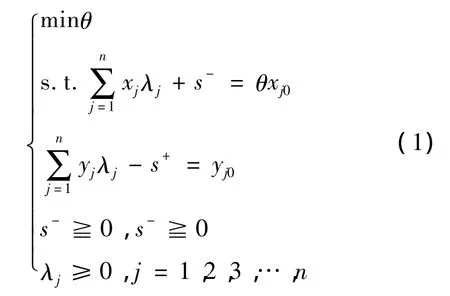
其中θ为DMUj0的效率值，当模型(1)的最优解满足 θ=1，此时决策单元为弱 DEA［4－7］有效;若最优解满足θ=1，且s+=s－=0，则此决策单元为DEA有效;若θ＜1，则此决策单元为DEA非有效。

Charnes在文献［8］中提出可通过超效率DEA模型将决策单元集(记为S)里的决策单元分为两类:一类为前沿面决策单元(frontier DMUs)集(记为P);另一类是非前沿面决策单元(non-frontier DMUs)集(记为Q)。前沿面决策单元集P由3个集合E，E'和F组成。其中集合E由极有效(extreme efficient)决策单元组成;集合E'由有效但非极有效(efficient but not an extreme point)决策单元组成;集合F由弱有效决策单元(weakly efficient)组成，即P=E∪E'∪F。显然，前沿面决策单元都是有效或弱有效的，非前沿面决策单元都是非有效的。对不同类型的决策单元分别记为:

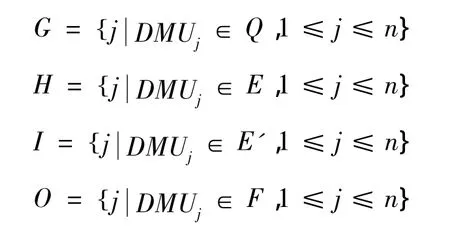
2 弱有效决策单元对效率值的影响

文献［1］指出:当判断决策单元集中的某一个DMUj效率值时，只有其中的有效DMUs会对DMUj效率值产生影响，而非有效DMUs对DMUj效率值不产生影响，即当增加或减少的DMUj∈Q(j∈G)，DMUj不影响对其他决策单元的效率值。下面给出弱有效DMUs对其他DMUs效率值影响的结论。

定理1设DMUj1∈F(j1≠j0)，如果 DMUj0在模型(1)中的最优解为 λ0，s－0，s+0，θ0，在模型(2)中的最优解为 λ*，s－*，s+*，θ*，则有 θ*= θ0。

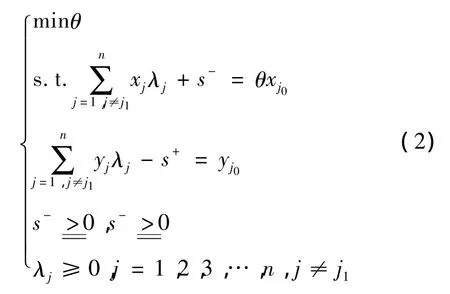
证明:设DMUj0在模型(2)中的最优解为λ*，s－*，s+*，θ*，则在 λ*中第 j1个分量位置增加一个0，记为，即 λ*=(λ*，…，，…，)T变为=(，…，，0，，…，)T。显然，s－*，s+*，θ*为模型(1)的一个可行解，且有

又因为DMUj1∈F(j1≠j0)，即决策单元DMUj1在决策单元集S中为弱有效的，其输入向量为xj1，输出向量为yj1，由“DEA生产可能集锥性公理以及有效性与DMU同倍增长无关定理”可知:必存在DMUj2∈S，且满足(xj1，－ yj1)≥k(xj2，－ yj2)，其中k ＞0，且为常数。设 λ1，s－1，s+1，θ1为 DMUj0在模型(1)中的某个可行解，则其中的约束条件满足:

同理，在模型(1)中约束条件也满足

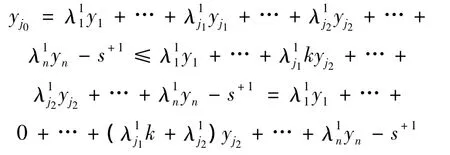
显然存在s1+*≥s+1，满足

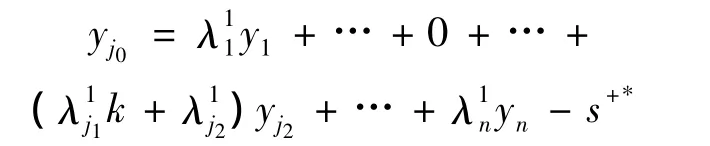
因此，DMUj0在模型(1)中的任意一个可行解λ1，s－1，s+1，θ1均对应模型(2)的一个可行解，其中

设DMUj0在模型(1)中的所有可行解θ的集合为{θ1，θ2，θ3…}，则在模型(2)中可得对应可行解θ的集合为…}，且满足 θi≥(i=1，2，3，…)，又因为 θ0=min{θ1，θ2，θ3…}，min{…}≥θ*，由以上证明中 θ1的任意性，有

由式(3)、(4)可推出θ0=θ*，定理成立。

定理1说明在用CCR模型判断DMUj0的有效性时，如DMUj1为DEA弱有效，则将DMUj1从决策单元集S中剔除，不影响DMUj0的效率值。将以上结论推广到决策单元集S中所有的弱有效决策单元，则有以下结论:

推论1设DMUj0(j0∉O)在模型(1)中的最优解为 λ0，s－0，s+0，θ0，在模型(5)中的最优解为λ*，s－*，s+*，θ*，则有 θ*= θ0。

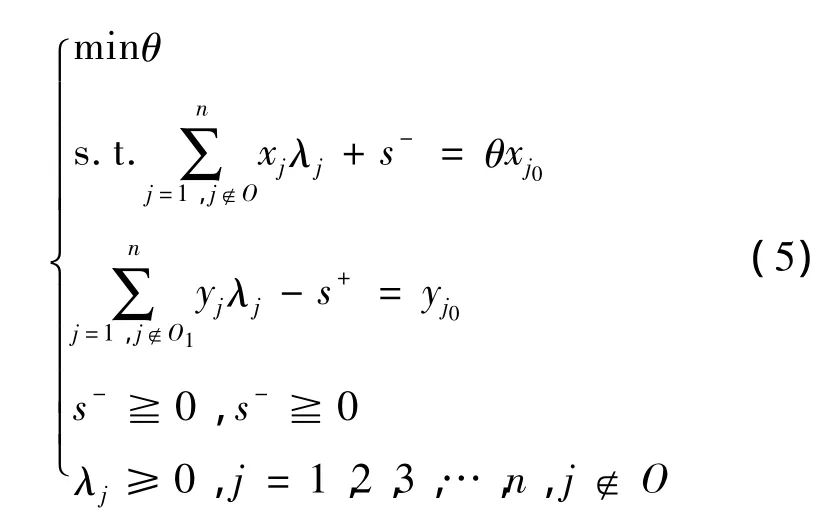
证明 在模型(1)中依次减去一个弱有效决策单元，由定理1可知效率值不变。

推论1说明在评价DMUj0有效性时，决策单元集中的弱有效决策单元不对DMUj0的效率值产生影响。

综合定理1和推论1，易得如下推论:

推论2设DMUj0(j0∉O，j0∉G)在模型(1)中的最优解为 λ0，s－0，s+0，θ0，在模型(6)中的最优解为 λ*，s－*，s+*，θ*，则有 θ0= θ*。

推论2说明在评价DMUj0有效性时，决策单元集里的非有效单元和弱有效单元不对评价结果产生影响。

综上可知，决策单元集里非有效和弱有效决策单元不会对其他决策单元的效率值产生影响。因此，当利用DEA评价系统对新的决策单元进行有效性评价时，可以将非有效和弱有效决策单元从原评价系统的决策单元集里剔除。这样既减少了评价系统里的决策单元数量，简化了计算，又不影响评价结果。

3 算例分析

有决策单元如表1所示。

表1 决策单元的输入和输出数据

由超效率模型可知:决策单元1，2和6为极有效决策单元;决策单元5，8为有效但非极有效决策单元;决策单元3，9为弱有效决策单元;决策单元4，7为非有效决策单元。用集合表示分别为:E={DMU1，DMU2，DMU6}，E'={DMU5，DMU8}，F={DMU3，DMU9}，Q={DMU4，DMU7};决策单元下标集合分别为:G={4，7}，H={1，2，6}，I={5，8}，O={3，9}。

选取决策单元1，4，8，将所有决策单元作为参考集，即利用模型1所得结果见表2。

表2 模型1计算结果

将非有效决策单元7从决策单元集中移除，得

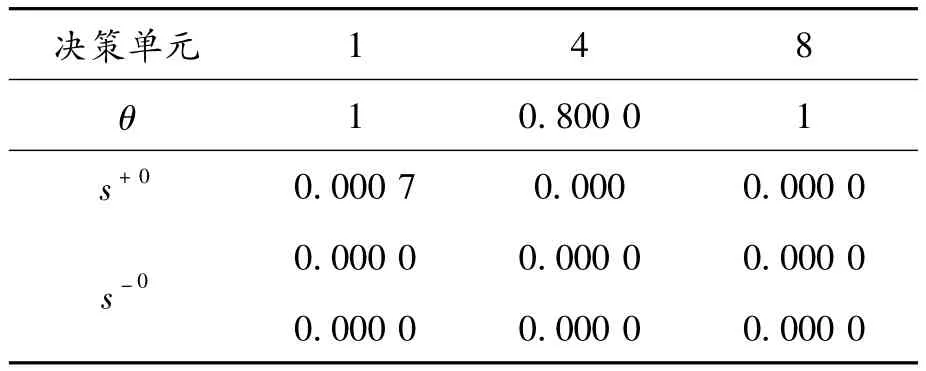
表3 效率值计算结果

由表3可知决策单元1，4和8的效率值无变化。

将弱有效决策单元3，9从决策单元集中移除，得

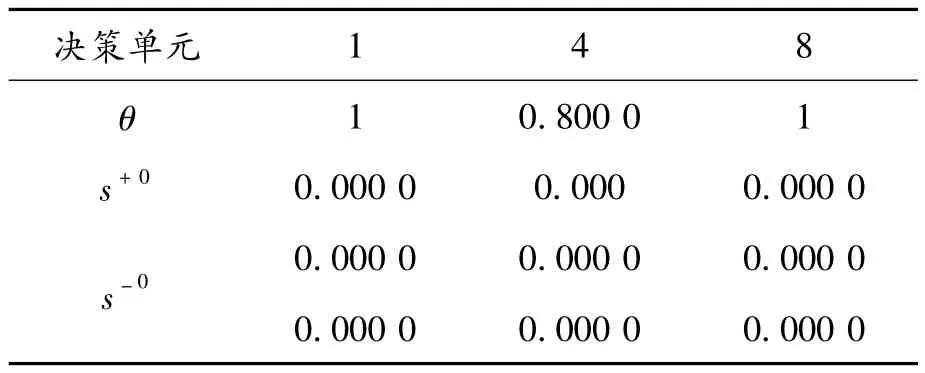
表4 模型7计算结果

决策单元1，4和8的效率值也无变化。

4 结束语

本文讨论了CCR模型在增加决策单元和减少决策单元时的灵敏度分析，得出了以下结论:增加的决策单元有效性由决策集里的有效单元(不包括弱有效决策单元)决定，减少的决策单元如果是非有效单元或弱有效单元，则不改变其余决策单元的有效性，最后通过一个算例验证了结论。在评价新的决策单元有效性时，如果决策系统里的决策单元较多，利用本文结论，可以剔除对需评价的新决策单元不产生影响的决策单元，从而减少决策系统里的决策单元数量，在没有改变评价结果的条件下减少了评价的计算量。通过对本文定理1和定理2的证明，可以发现在DEA理论中，决策系统中决策单元的地位并不相同，弱有效决策单元集和非有效决策单元集对于决策单元的效率值并不产生贡献。

［1］张俊容，郭耀煌.Pareto有效在 DEA模型中的应用［J］.系统工程理论方法应用，2002，11(2):165－168.

［2］吴怡之，全东平，许红安，等.基于 Pareto多目标优化的工业传感网路由协议研究［J］.计算机科学，2011，38(4):100－103.

［3］Charnes A，Cooper W W，Thrall R M.A structurefor classifying and characterizing efficiencies and inefcienciesin DEA［J］.Journal of Productivity Analysis，1991(2):197－237.

［4］王金山，倪敏.一种新的带有参数的DEA有效单元排序模型［J］.运筹学学报，2010，14(4):68－74.

［5］Jahanshahloo G R，Hosseinzadeh Lotfi F，Shoja N，et al.Sensitivity analysis of inefficient units in data envelopment analysis［J］.Mathematical and Computer Modelling，2011，53(5):587－596.

［6］王开荣，徐广业，南春梅.DEA有效单元排序的一种新方法［J］.数学的实践与认识，2011，41(16):125－132.

［7］马占新，木仁.基于有效样本视角下的DEA方法［J］.内蒙古大学学报:自然科学版，2011，42(3):241－246.

［8］Andersen P，Petersen N C.A procedure for ranking efficient units in data envelopment analysis［J］.Management Science，1993，39(10):1261－1268.