一类奇异积分算子及交换子在变指数 Herz空间上的有界性

李露露，陶双平

(西北师范大学数学与统计科学学院，兰州 730070)

给定一个开集E⊂Rn和一个可测函数q(x):E→［1，∞)，则变指数Lebesgue空间Lq(·)(E)定义为:

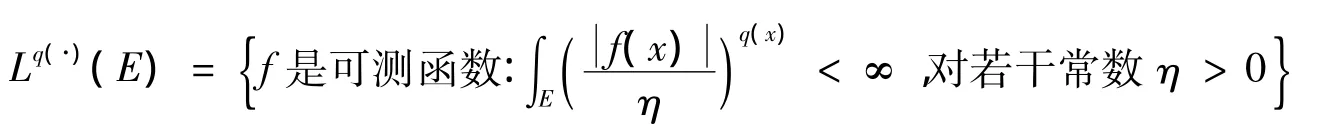
并赋予范数:

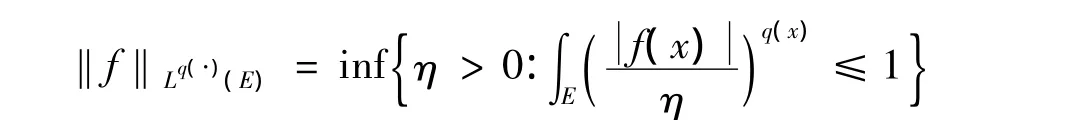
当q(x)=q0是常数时，Lq(·)(E)就是经典的Lq0(E)。

归功于Kováˇcik和Rákosn r'k在文献［1］中建立了变指数函数空间的一些基本性质，在最近20多年中，关于算子在变指数函数的有界性研究有了很大的突破，详见文献［2-11］。其中最令人欣喜的结论之一是建立了Hardy-Littlewood极大算子在变指数的Lebesgue空间中的有界性。最近，Cruz-Uribe-SFOFiorenza-Martell-Pérez在文献［3］中论证了调和分析中的许多经典算子在变指数的Lebesgue空间中的有界性结论，诸如sharp极大算子、乘子算子、平方函数算子、数次积分算子等。

令Ω是零次奇次的，在单位球Sn-1上无穷可微的，且满足则奇异积分算子T定义为:

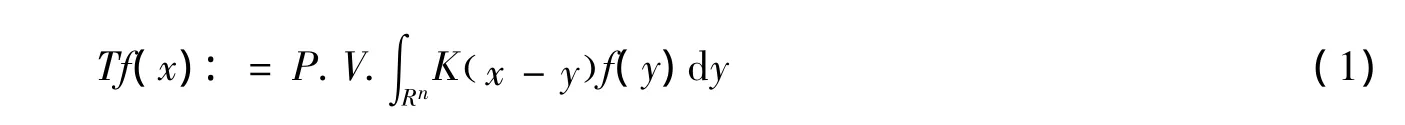
由算子T和一个函数b生成的交换子［b，T］定义为:

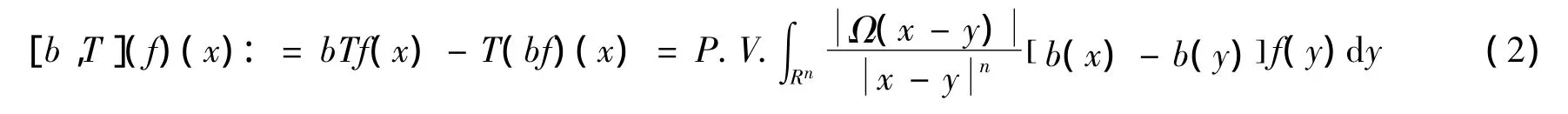
文献［3］和［12］分别证明了式(1)定义的算子T和当b∈BMO时式(2)定义的交换子［b，T］在变指数的Lebesgue空间中是有界的。本文考虑T和［b，T］在变指数的Herz空间中的有界性。通过在经典的Hardy空间中研究乘子的性质得到了经典的Herz空间，参见文献［13-15］。

1 预备知识

在这部分，将回顾一些定义并介绍一些证明中用到的一些引理。给定一个函数f∈L1loc(E)，则Hardy-Littlewood极大算子M定义为:

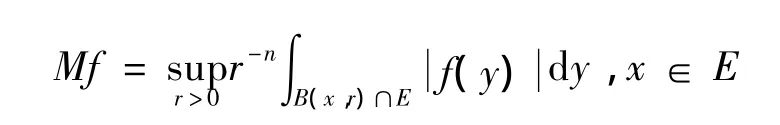
定义 1［12］

1)集合Ρ(Rn)表示由所有的可测函数q:E→［1，∞)组成，并且满足

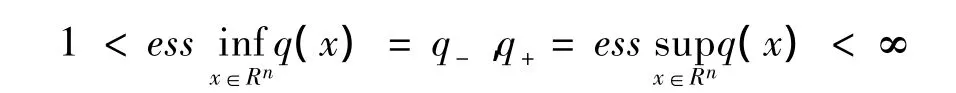
2)集合Β(Rn)表示由所有的可测函数q(x)∈Ρ(Rn)组成，并且满足Hardy-Littlewood极大算子M在 Lq(·)(E)上是有界的。

定义 2［16］令 α∈R，0≤λ ＜ ∞，0 ＜p ＜ ∞，并且 q(x)∈Ρ(Rn)，则奇次的 Herz空间定义为

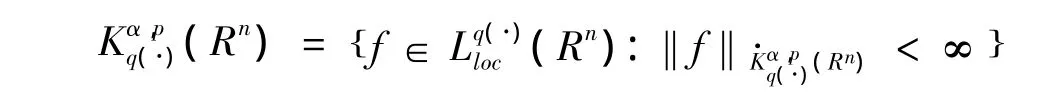
下面给出变指数的一些性质。Cruz-Uribe，SFO等在文献［4］以及Nekvinda在文献［10］中各自独立地证明了下面的充分条件。

引理1［4］若E是一个开集，如果q(·)∈Ρ(E)满足不等式:

其中C＞0是与x，y无关的常数，则有q(·)∈B(E)。

引理2［3］令q(x)∈Ρ(Rn)，则下面的条件互相等价:

① q(x)∈B(Rn);

② q'(·)∈B(Rn);

④ 对若干1＜q＜p-∈B(Rn);

引理 3［3］若 q(x)∈B(Rn)，则对任意的 f∈Lp(·)(Rn)，存在一个常数 C，使得

引理 4［12］若 q(x)∈B(Rn)，并且 b∈BMO(Rn)，则对任意的 f∈Lp(·)(Rn)，存在一个常数 C，使得

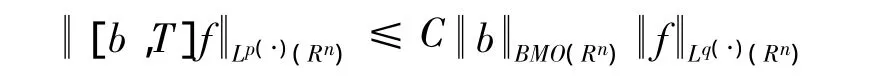
下面的引理描述了广义的 Hölder’s inequality和Lq(·)(E)的对偶空间。详细的证明见文献［1］。

引理5［1］若q(·)∈B(E)，则下面的事实成立。

1)(广义的 Hölder’s inequality)对所有的 f∈Lq(·)(E)和所有的 g∈Lq'(·)(E)，有

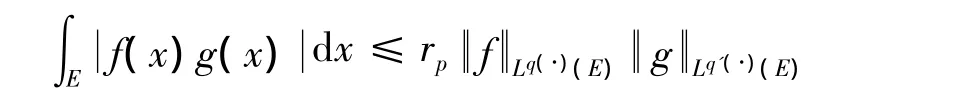
其中rp=

2)对所有的 f∈Lq(·)(E)，有

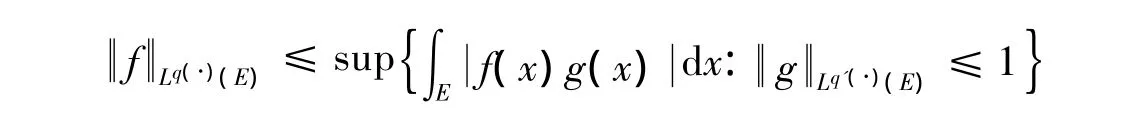
引理6［16］若q(x)∈B(Rn)，则存在一个正常数δ∈(0，1)和C＞0，对Rn中的所有的球B和所有的可测子集S⊂B，有

引理7［16］若q(x)∈B(Rn)，则存在一个正常数C＞0，使得对Rn中的所有的球B，有

引理 8［17］令 b∈BMO(Rn)，m∈N，i，j∈Z 并且 i＜ j。则有:

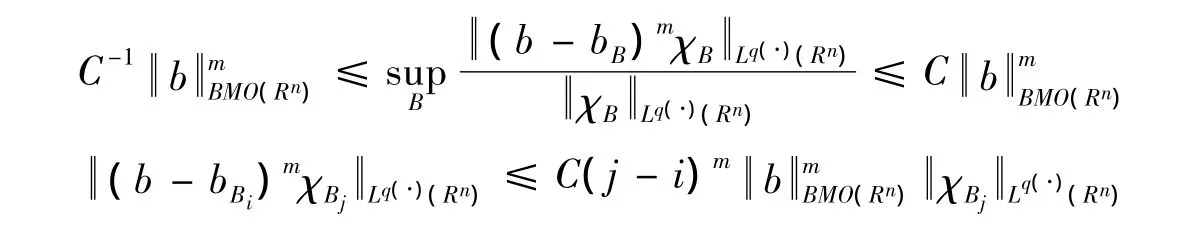
2 主要结论及其证明

令q(·)∈Ρ(Rn)，满足引理1中的条件(3)和(4)。q'(·)也满足同样的条件。特别的，由引理2可知 q(·)，q'(·)∈B(Rn)。因此，运用引理 6，当 q(·)，q'(·)∈B(Rn)，设 0 ＜ δ1，δ2＜1，对 Rn中的所有的球B和所有的可测子集S⊂B，有

全文中的δ1和δ2的定义如上所述。

本文的主要结论如下:

定理 1 若 q(x)∈B(Rn)，0 ＜ p≤∞ ，-nδ1＜ α ＜ -nδ2，则T 在上是有界的。

定理 2 若 b∈BMO(Rn)q(x)∈B(Rn)，0 ＜ p≤∞，-nδ1＜ α ＜ -nδ2，则［b，T］在(Rn)和(Rn)上是有界的。

下面给出定理1的证明。因为非奇次Herz空间上的证明类似于奇次Herz空间上的证明，所以只给出奇次空间上的证明。设 f∈(Rn)，并记

则有

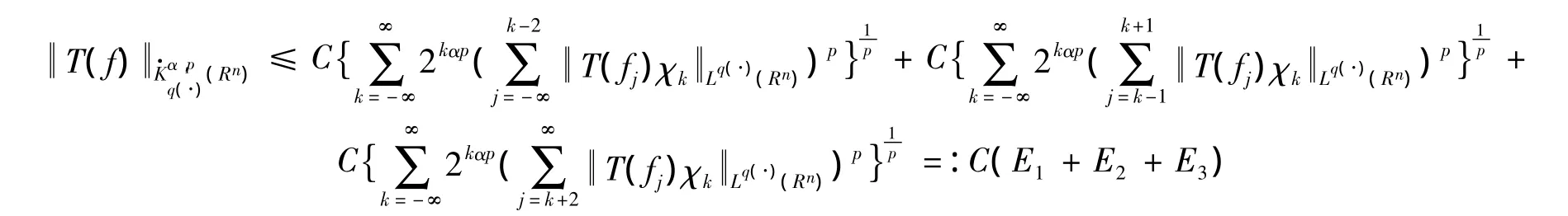
由引理3可知，算子T在Lp(·)(Rn)上是有界的，则

下面估计 E1。注意到当 x∈Ak，j≤k-2，y∈Aj时，有由于Ω是有界的，因此，由引理5有

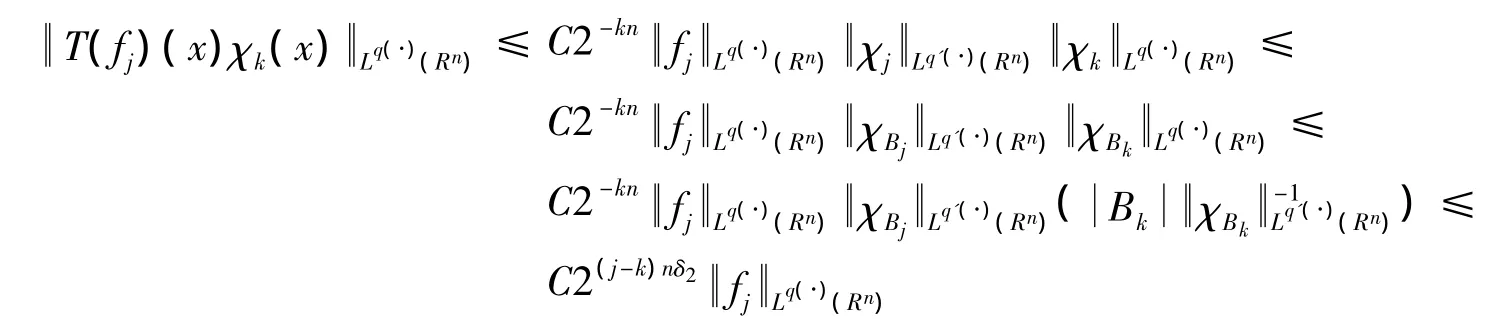
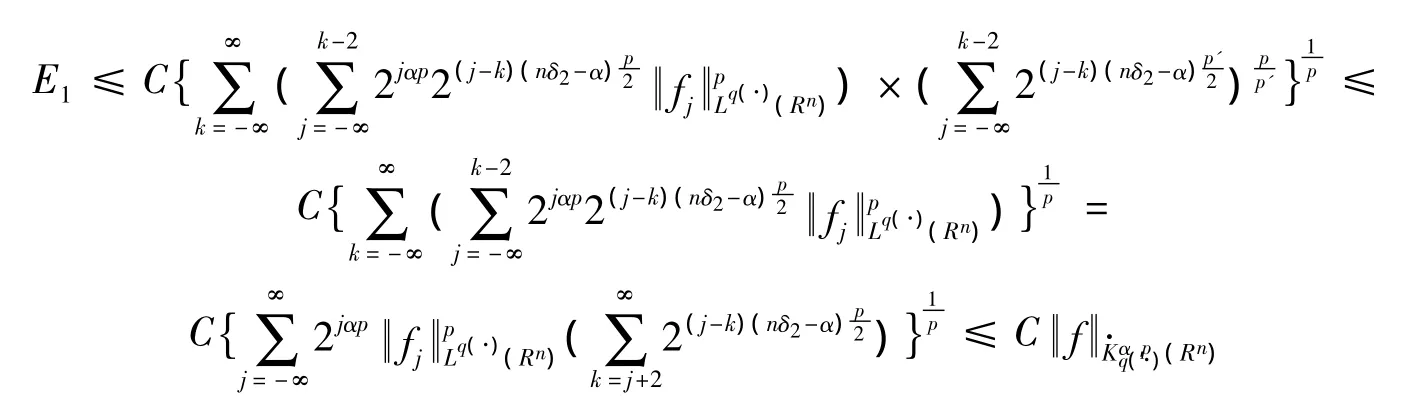
若0 ＜p≤1，则有

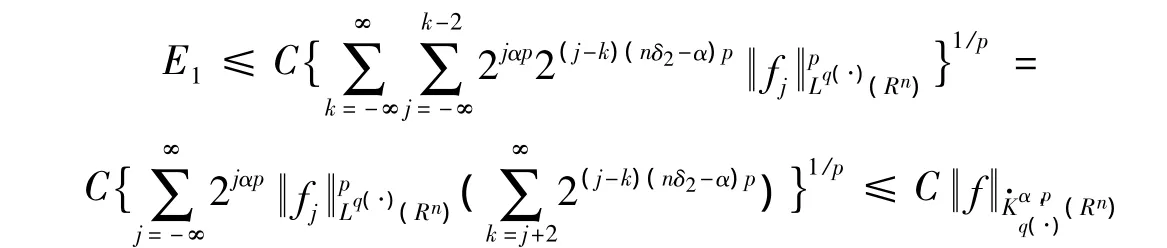
下面估计E3。注意到当x∈Ak，j≥k+2，当y∈Aj时，有因此，由引理5，有

类似于E1的估计，有

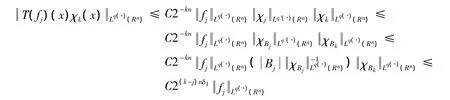
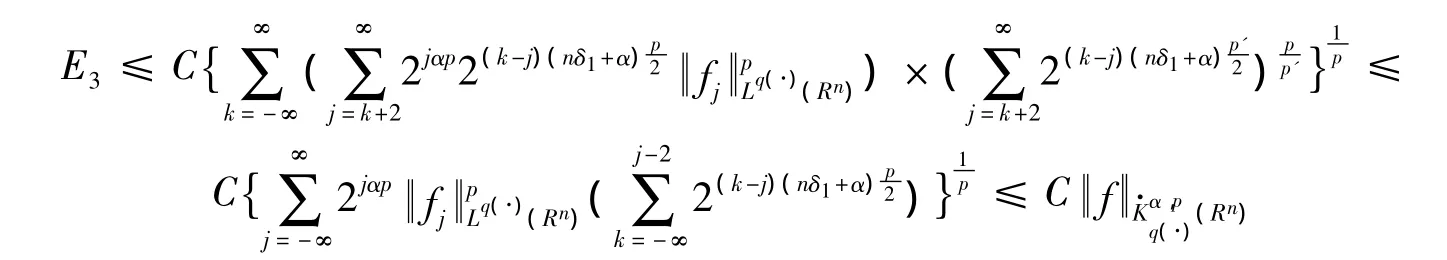
若0 ＜p≤1，则有

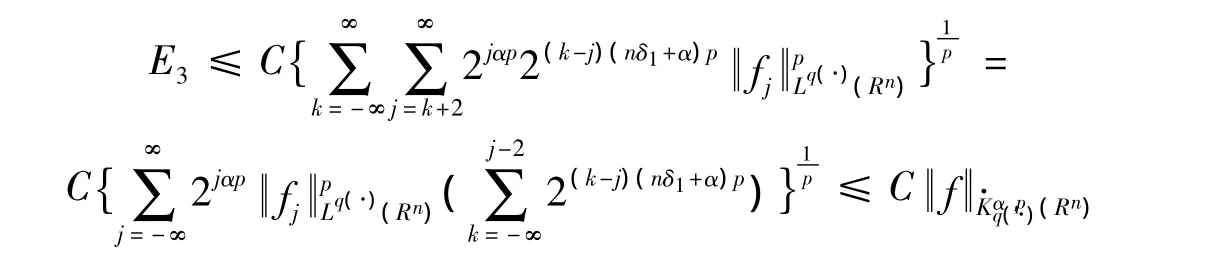
这样完成了对定理1的证明。

下面证明奇异积分交换子［b，T］在变指数Herz空间是有界的。类似定理1的证明，仅仅给出奇次情况下的证明。设，并记

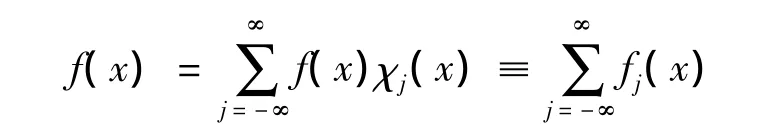
则有

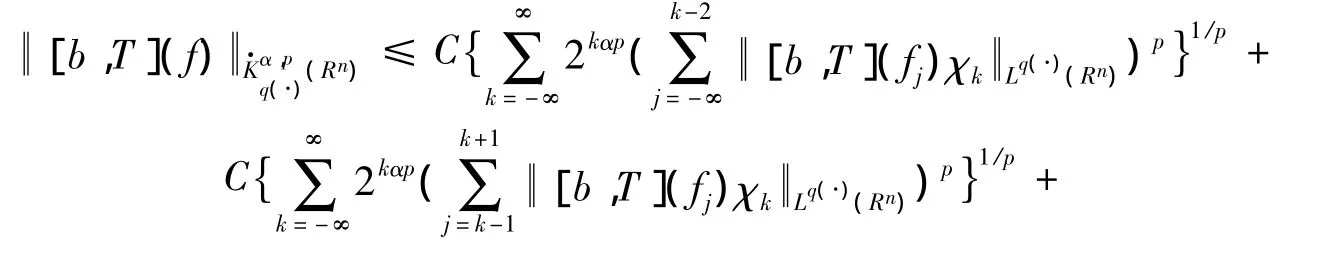
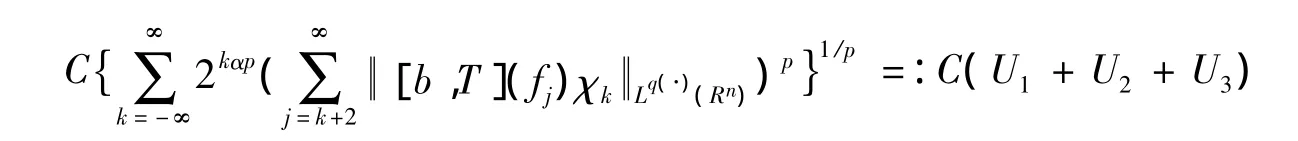
由引理4 可知，算子［b，T］在 Lp(·)(Rn)上是有界的，则

下面估计 U1。注意到当 x∈Ak，j≤k-2，y∈Aj时，有由于Ω是有界的，因此，由引理5，有

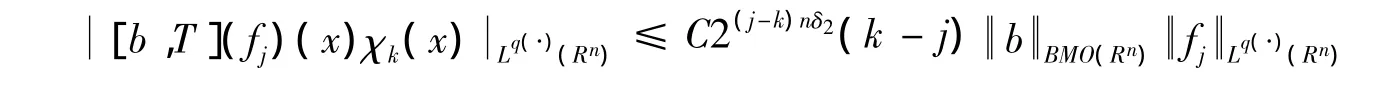
下面估计 U3。注意到当 x∈Ak，j≥k+2，y∈Aj时，有因此，由引理5，有

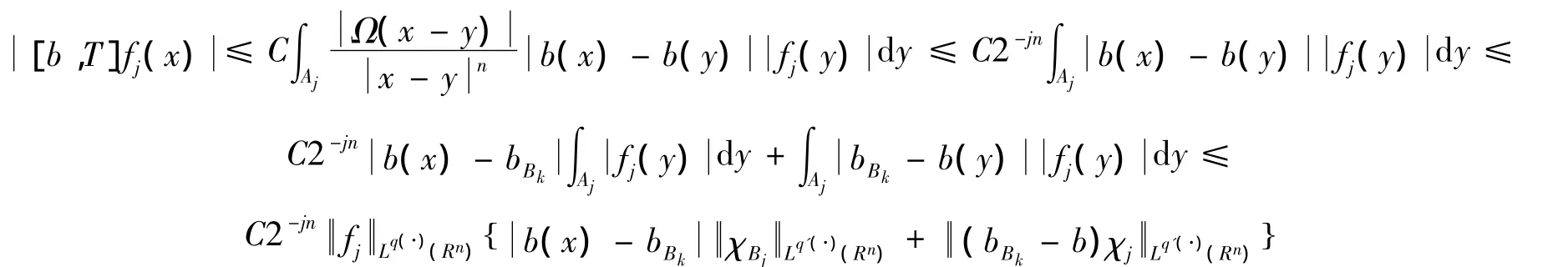
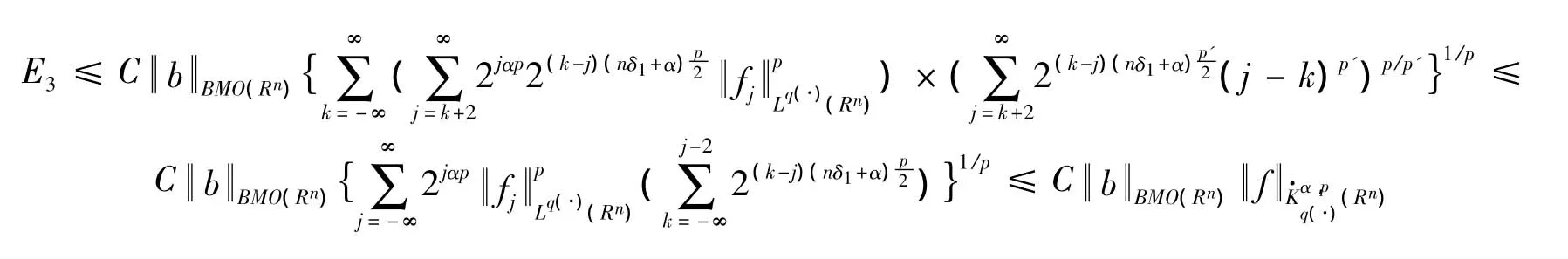
这样完成了对定理2的证明。

［1］Kováˇcik O，Rákosn r'k J.On spaces LP(x)and Wj，P(x)［J］.Czechoslovaj Math，1991，41(116):592-618.

［2］Cruz-Uribe D，Diening L，Fiorenza A.A new proof of the boundedness of maximal operators on variable Lebesgue spaces［J］.Bollettino della Unione Matematica Italiana，2009，2(1):151-173.

［3］Cruz-Uribe D，Fiorenza A，Martell J，et al.The boundedness of classical operators on variable LPspaces［J］.Ann Acad Sci Fenn Math，2006，31:239-264.

［4］Cruz-Uribe D，Fiorenza A，Neugebauer C.The maximal function on variable LPspaces［J］.Ann Acad Sci Fenn Math ，2003，28:223-238.

［5］Diening L.Maximal functions on Musielak-Orlicz spaces and generalized Lebesgue spaces［J］.Bull Sci Math，2005，129:657-700.

［6］Diening L.Maximal functions on generalized Lebesgue spaces LP(·)［J］.Math Inequal Appl，2004，7:245-253.

［7］Diening L，Harjulehto P，Hästö P，et al.Maximal functions in variable exponent spaces:limiting cases of the exponent［J］.Ann Acad Sci Fenn Math，2009，34:503-522.

［8］Kopaliani T.Infimal convolution and Muckenhoupt AP(·)condition in variable LPspaces ［J］.Arch Math，2007，89(2):185-192.

［9］Lerner A.On some questions related to the maximal operator on variable LPspaces［J］.Trans Amer Math Soc，2010，362:4229-4242.

［10］Nekvinda A.Hardy-Littlewood maximal operator on LP(Rn)［J］.Math Inequal Appl，2004，7:255-265.

［11］Pick L，Ruˇziˇcka M.An example of a space LPon which the Hardy-Littlewood maximal operator is not bounded［J］.Expo Math，2001，19:369-371.

［12］Karlovich Yu，Lerner K.Commutators of singular integrals on generalized LPspaces with variable exponent［J］.Publ Mat，2005，49:111-125.

［13］Lu S，Yang D.The decomposition of the weighted Herz spaces and its application［J］.Sci China(A)，1995，38:147-158.

［14］Li X，Yang D.Boundedness of some sublinear operators on Herz spaces［J］.Illinois J Math，1996，40:484-501.

［15］Hernández E，Yang D.Interpolation of Herz spaces and applications［J］.Math Nachr，1999，205:69-87.

［16］Izuki M.Commutators of fractional integrals on Lebesgue and Herz spaces with variable exponent［J］.Rendicontidel Circolo Matematico di Palermo，2010，59:461-472.

［17］Izuki M.Fractional integrals on Herz-Morrey spaces with variavle exponent［J］.Hiroshima Math J，2010，40:343-355.