基于主从同步的欠驱动AUV与移动平台水下对接控制
刘俊杰,陈 虹,王 磊
(武汉第二船舶设计研究所,湖北 武汉430205)
0 引 言
水下自主航行器(AUV)是一种自带能源,依靠自治能力管理与控制自身运动,执行海洋任务的水下机器人。使用水下移动平台为AUV 进行能量补充、信息读取和维护保障,对延伸AUV 作业空间、扩展作业能力起到非常重要的作用。而AUV与移动平台的动态对接控制,是AUV 成功回收须解决的关键技术之一。
AUV与水下移动平台的回收过程与无人机空中加油过程[1]相似:对接过程分为对接双方产生编队以及保持编队2个步骤。因而可以将AUV水下对接过程分为2个阶段:第1 阶段是AUV 由远及近,跟踪目标并达到与目标运动同步的状态;第2 阶段是AUV与目标保持同步运动的状态,当目标的运动受到扰动,AUV 能够迅速跟踪目标轨迹,使AUV与对接装置的位置误差在对接许可范围之内。其中,水下移动对接成功的关键在于第2 阶段:在海流干扰影响下,两者近距离相互运动时,AUV 保持在回收装置的捕捉范围内运动的能力。
AUV与移动平台的水下动态对接是一个复杂的过程,实际航行中,通信、海流与流场造成的水流干扰以及对接装置的捕捉范围均是影响回收成功的重要因素。目前学术界大多研究AUV与水下固定目标对接,并主要关注AUV与回收装置的位置控制:如薛源[2]、高剑等[3]分别使用视线导引法、横向跟踪法和人工矢量场法等方法使AUV 沿回收器中轴线运动并最终进入回收器;Teo 等[4]使用扩展卡尔曼滤波器估计水流和自身运动状态,并使用模糊控制方法控制AUV 在不确定海流环境下回收到固定回收器中。
由于固定目标回收器一般置于水底,来自水流干扰、AUV与回收平台之间的流场干扰以及通信设备所受影响均较小,因而AUV 能够得到目标和自身精确的相对距离,并且能够稳定地控制自身运动,其回收较为简单。而与移动目标对接时,系统的对接环境具有不确定性,造成水下探测和通信设备的工作效果受到严重限制,难以获得目标与AUV 之间的精确距离;而目标与AUV 本身运动也会受到来自环境的不确定水流以及两系统相互运动造成的流场干扰的影响。因而AUV与固定目标的回收方法不能直接用于AUV与移动平台的对接,AUV与移动目标对接控制仍是一个复杂,亟待研究的领域。
吴泽伟[5]以AUV与母艇同步运动的方式描述水下回收过程,但所选择的AUV为全驱动模型,而实际应用中,AUV 常因能源限制设计为欠驱动系统,其运动控制更加困难;并且该文献考虑的是通信精确无误情况下的回收,而实际对接过程中,水下探测和通信受到严重限制,AUV 所获得的目标运动信息常带有噪声或缺失。
本文采用主从式同步策略进行AUV 跟踪移动平台并与之同步运动控制。将动力学特性较慢的目标母艇作为主动体,动力学特性较快的AUV 作为从动体,使主动体系统输出作为从动体指令信号输入,即令从动体跟踪主动体的运动状态,从而实现主动体和从动体运动的协调一致,并满足相应的运动学限制条件。针对AUV与移动平台对接过程中AUV与目标保持同步运动阶段,采用卡尔曼滤波器估计目标运动状态,设计基于主从式同步位置跟踪的离散滑模控制器驱动AUV 同步跟踪目标,仿真证明该控制过程的有效性。
1 AUV与目标水平运动建模
假设母艇和AUV 均为刚体,母艇回收装置与母艇刚性连接,且与AUV 在同一水平面上。考虑母艇和AUV 做水平面运动,且令AUV 处于水平平衡态,其重心与浮心重合,其垂直速度w、俯仰角速度q 及横摇角速度p 均视为0,由AUV 六自由度动力学方程可简化得到AUV 水平面非线性运动方程[6]:
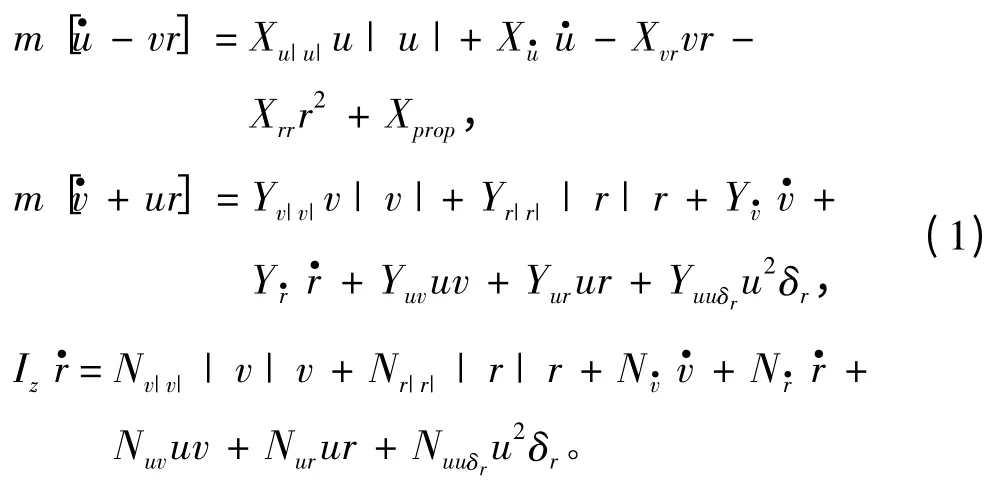
对应水平面运动学方程为:
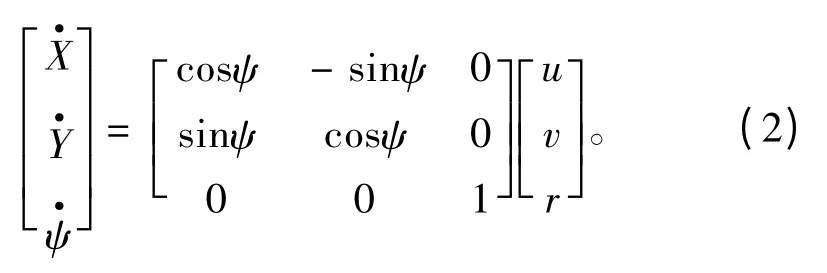
在AUV与母艇的近距离跟踪保持阶段,两者保持相同前向速度运动,主要进行横向距离跟踪,因而首向角ψ 变化一般较小,其横向距离Y 运动学方程可简化为[7]:

使用小偏差法对AUV 水平面非线性运动方程进行线性化,AUV 定常运动时,前向速度u 视为常值,忽略前向速度u 对横向运动的影响;横向速度v、首向角速度r为小量,忽略式中两者的高阶项。由式(1)和式(3)可得AUV 水平面增广运动方程:
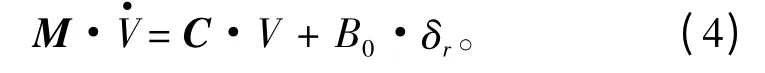
其中
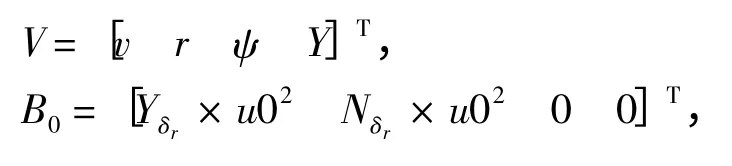
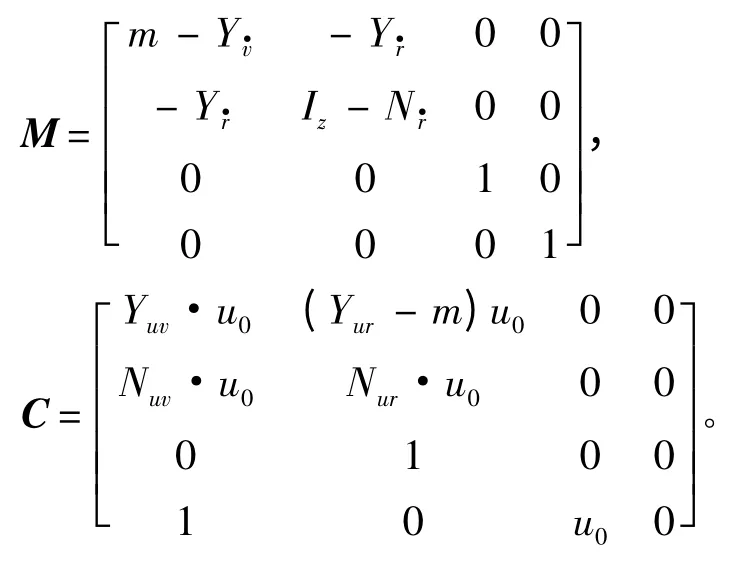
其中V为AUV 水平面运动状态变量,δr为AUV垂直舵角度输入,u0为AUV 平衡态时的前向速度;m,IZ分别为AUV 质量和转动惯量,Yv·,Yr·,Nr·为附加质量,Yvv,Yrr,Yuv,Nrr,Nvv,Nuv等分别为AUV 轴向阻尼和横向阻尼,Yδr,Nδr为AUV 舵升力系数。
选择潜艇为AUV 回收平台,其水平面运动方程[8]与式(4)形式相似:
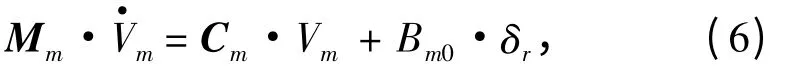
其中
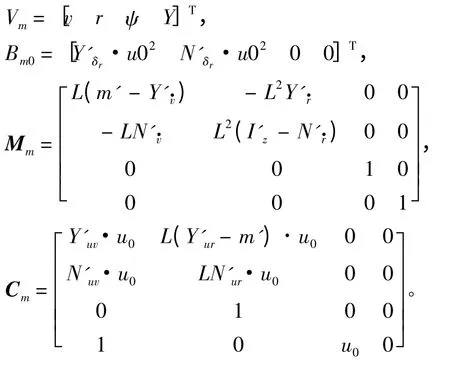
其中Vm为潜艇水平面运动状态变量;δr为潜艇垂直舵输入;u0为潜艇平衡态时的前向速度;矩阵Mm和Cm内的参数为潜艇质量、转动惯量、附加质量及阻尼的无因次化值。
2 AUV 同步跟踪移动目标控制律设计
针对回收过程第2 阶段AUV的运动控制,考虑到AUV 在实际运行时,控制系统所处理的信息均为数字信号,采用离散滑模设计AUV 同步跟踪目标位置控制器。针对目标运动系统的观测噪声、过程噪声以及与AUV信息传输时存在的通信噪声,均假定为目标运动系统中的过程和观测高斯白噪声,并使用卡尔曼滤波方法对包含噪声的目标运动系统进行估计。基于所估计的目标状态及所设计的离散滑模控制器,通过控制AUV与目标状态的偏差为0 达到AUV 同步跟踪目标的目的。
对公式进行矩阵变换并离散化,则AUV 运动状态离散方程描述为:
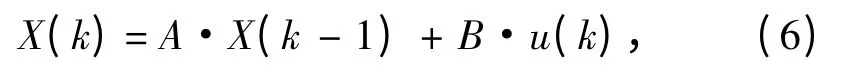
对公式进行矩阵变换并离散化,则潜艇状态方程及测量方程描述为:
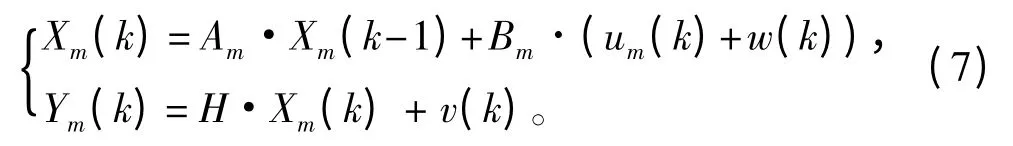
令潜艇状态方程的过程随机干扰w(k)为服从高斯分布的、均值为0 且协方差阵为Q的系统噪声;测量误差v(k)为服从均值为0 且协方差为R的高斯分布。其中,设计H=Im。
对潜艇离散控制系统使用卡尔曼滤波器递推算法对其输出Ym(k)进行估计:
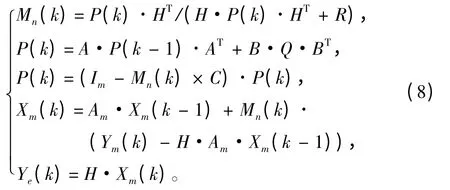
使用k 时刻母艇状态的估计值Ye(k)代替真实状态Xm(k),令e(k)= Ye(k)- X(k),母艇的控制输入um(k)为预先给定,且可观测。
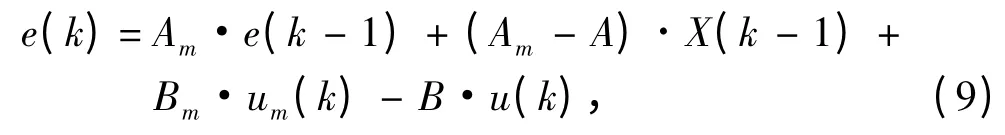
由式(4)和式(5)可知,秩rank[B0]≠rank[B0,Bm0]= rank[B,(Cm- C)],因而对矩阵变化后的式(6)和式(7)有:秩rank[B]≠rank[B,Bm]=rank[B,(Am- A)]。两者模型参数不满足匹配性条件,因而对于误差系统(9),其控制u(k)对于摄动项(Am- A)·X(k -1)+ Bm·um(k)并不具备不变性。这是由于AUV为欠驱动系统,在外部非定常干扰及系统摄动条件下不能完全跟踪母艇运动状态。
以横向距离Y为输出观测项,对其进行极点配置,选取切换函数S(k)=C·e(k),针对偏差方程,计算其等效控制:
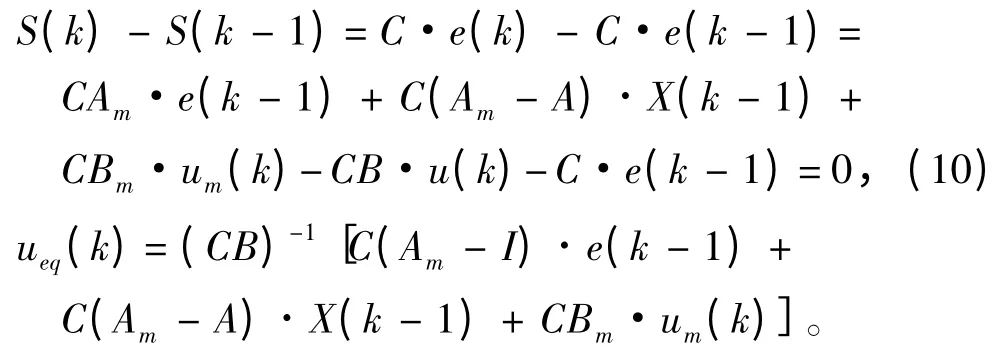
设计指数趋近律:(S(k)- S(k -1))/T= - ε·sgn(S(k))- q·S(k),T为控制系统采样时间。
则可获得针对误差系统的控制输入u(k)为:
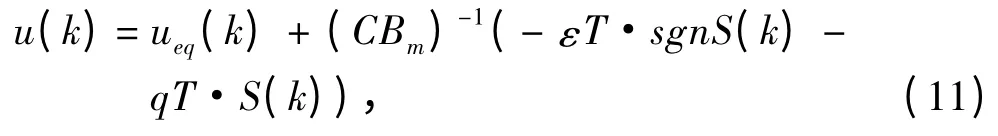
使用李亚普洛夫稳定性定律计算离散切换控制律的稳定性。状态轨迹进入滑模区S(k)=0的必要条件和状态轨迹收敛到S(k)=0 上的收敛条件分别为:
对于式(12)中必要条件(1),当ε,q >0 时等式成立;对于收敛条件(2)有:
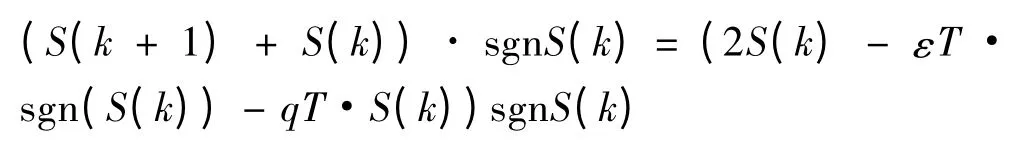
当S(k)>0 时,有S(k)>εT/(2 - qT);
当S(k)<0 时,有S(k)<- εT/(2 - qT),2 -qT >0;
即
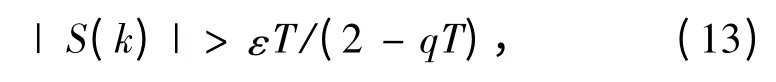
当满足式(13)时,误差系统能沿滑模面收敛于平衡点,而当| S(k)|≤εT/(2 -qT)时,会出现幅值为εT/(2 - qT)的抖振[9]。为减弱式(13)引起的抖振,使用饱和函数 satS(k)代替符号函数sgnS(k),
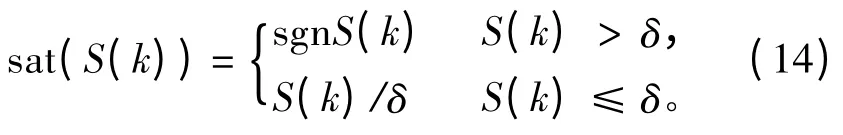
仍使用式(12)的离散滑模稳定性判别方法,可证明δ >εT/(2 -qT)时,所选择控制律可使控制系统稳定趋近于平衡点。
3 仿真结果
为验证本文主从式同步控制方案,使用Matlab软件进行回收系统的建模与仿真。其中式(5)中潜艇水平面运动模型参数[8]为:

式(4)中AUV模型参数为:

选取滑模切换面参数C=[0.2 1.7 3.7 4.5],选取控制律参数为ε = 0.1,q = 16,δ = 0.1,T =0.01。设定潜艇运动输入舵角为0,初始状态下两者均以纵向速度u0=1.5 m/s的速度航行,横向距离为1 m,横向速度和首向角速度初始值为0;水平海流流速为0.5 m/s,流向为90°;选取w(k),v(k)分别为幅值±0.5和±0.1的高斯白噪声,其对应协方差设计为Q=0.25,R=100* I4。
依照上述参数进行Matlab 程序仿真,仿真结果为:
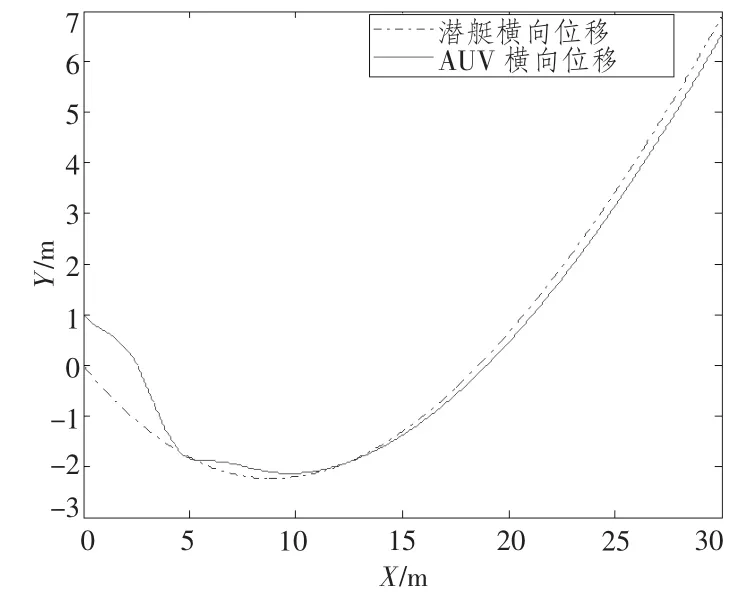
图1 AUV与母艇横向距离跟踪Fig.1 Cross-tracking between AUV and submarine
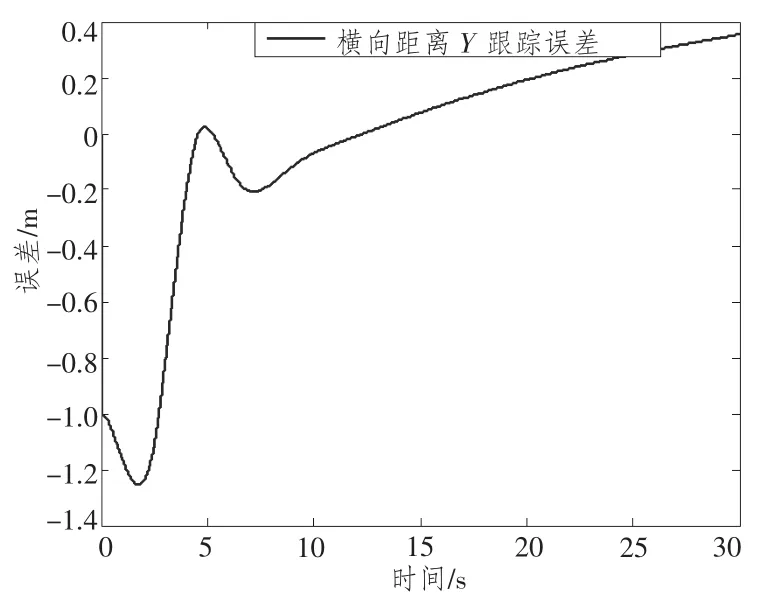
图2 AUV与母艇横向距离跟踪误差Fig.2 The cross-tracking errors of the system
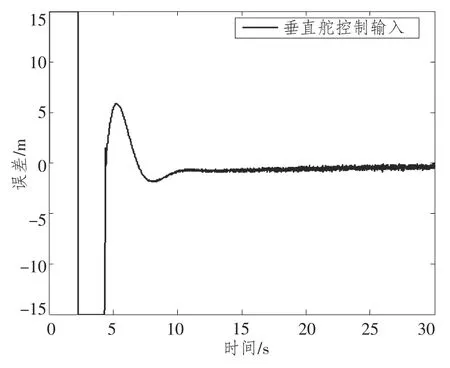
图3 AUV 垂直舵舵角控制输入Fig.3 The vertical rudder input of AUV
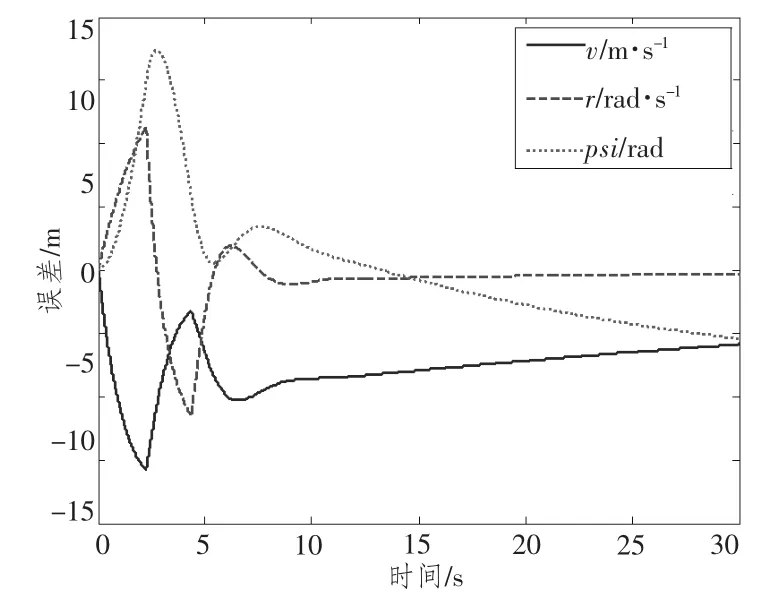
图4 AUV与母艇状态跟踪误差Fig.4 State-track errors of AUV and submarine
分析图1和图2 仿真结果可知,当主从系统受水平面常值水流干扰时,AUV与母艇横向距离跟踪误差迅速减小趋于0,稳定后,横向偏差随时间缓慢增加,但在仿真时间内能够保持在0.3 m 以内,即所设计的控制器能够保证AUV与回收装置对接。由图4 可知,AUV 跟踪母艇时,两者依然存在横向速度和首向角差值,这是由于AUV与母艇的动力学特性不同造成的:在相同的水流扰动下,潜艇和AUV的状态响应不同,而欠驱动AUV 在垂直舵单输入情况下不能同时跟踪目标潜艇的位置和姿态。
4 结 语
本文基于主从式同步思想描述AUV与水下移动平台的对接过程,设计了在水平常值海流扰动下,AUV 同步跟踪目标运动轨迹的离散滑模控制器,并使用卡尔曼滤波进行目标轨迹预测。仿真结果表明,AUV 能够同步跟踪移动平台的位置值,保持在回收装置捕捉范围之内运动。
本文仅针对水平面常值海流扰动情况下的AUV与移动平台的对接问题进行仿真,而实际对接过程是AUV与移动平台的空间相互运动,且面临流速不确定的海流干扰和运动刚体之间的流场干扰;对接时AUV的姿态也是影响回收装置捕捉AUV的重要因素之一。后期将进一步考虑AUV与移动平台在不确定海流下的垂向和纵向位置跟踪问题、同步过程中AUV的姿态控制问题,以及滑模控制器进行AUV 非线性系统的控制的适应性问题。
[1]李大伟,王宏伦.无人机自动空中加油飞行控制技术[J].系统仿真学报,2010(S1):130-134.LI Da-wei,WANG Hong-lun.UAV flight control in automated aerial refueling [J].Journal of System Simulation,2010(S1):130-134.
[2]薛源,严卫生,高剑,等.基于人工矢量场的AUV 自主回收路径规划[J].鱼雷技术,2011(2):26-30.XUE Yuan,YAN Wei-sheng,GAO Jian,et al.A path planning method based on artificial vector field for autonomous recovery of AUV[J].Torpedo Technology,2011(2):26-30.
[3]高剑,严卫生,徐德民,等.自主水下航行器的回坞导引和入坞控制算法[J].计算机工程与应用,2012,48(3):7-9.GAO Jian,YAN Wei-sheng,XU De-min,et al.Homing guidance and docking control algorithm for autonomous underwater vehicles [J].Computer Engineering and Applications,2012,48(3):7-9.
[4]KEN T,EDGAR A,PIERRE-PHILIPPE J B.A robust fuzzy autonomous underwater vehicle (AUV)docking approach for unknown current disturbances[J].IEEE Journal of Oceanic Engineering,2012,37(2):143-155.
[5]吴泽伟,吴晓锋.基于有限时间系统同步的自治水下航行器回收控制[J].自动化学报,2013,39(12):2164-2169.WU Ze-wei,WU Xiao-feng.Recovery control for autonomous underwater vehicle based on Fnite-time synchronization of systems[J].Acta Automatica Sinica,2013,39(12):2164-2169.
[6]FOSSEN T I.Marine ontrol systems:guidance,navigation and control of ships,rigs and underwater vehicles[M].Trondheim,Norway,2002.
[7]TIMOTHY P.Verification of a six-degree of freedom simulation model for the REMUS autonomous underwater vehicle[D].Massachusetts Institute of Technology and the Woods Hole Oceanographic Institution,2001.
[8]常赛.潜艇近水面航行控制方法研究[D].哈尔滨:哈尔滨工程大学,2011.
[9]宋立忠,陈少昌,姚琼荟.单输入不确定系统离散变结构控制[J].海军工程大学学报,2003(2):37-42.SONG Li-zhong,CHEN Shao-chang,YAO Qiong-hui.Discrete variable structure control for single-input uncertain systems[J].Journal of Naval University of Engineering,2003(2):37-42.

