NP569484-NP644537圆锥滚子轴承滚子-滚道凸度有限元分析

吴飞科,刘　赛,严剑刚,杨国策,宋钰蕾

(上海第二工业大学工程训练中心,上海201209)

NP569484-NP644537圆锥滚子轴承滚子-滚道凸度有限元分析

吴飞科,刘赛,严剑刚,杨国策,宋钰蕾

(上海第二工业大学工程训练中心,上海201209)

圆锥轴承滚子-滚道凸度设计包括轮廓设计和凸度量设计。在通用的对数凸型轮廓基础上,凸度量在滚子和滚道上的分配是一个有待研究的课题。通过计算特定工况下滚子-滚道的接触应力水平,来衡量设计的合理性。以NP569484-NP644537圆锥滚子轴承为例,用正交法分组,将取样轴承的内、外圈以及滚子的凸度分为若干匹配等级,并从中选取数种特征匹配;对各种匹配关系进行有限元分析,在保证有充分的接触长度的同时,接触应力应满足工程条件。

圆锥滚子轴承;载荷分布;接触应力;凸度设计;正交法;有限元分析

0　引言

圆锥滚子轴承因具有承载能力大、刚性好、可同时承受轴向与径向负荷、速度性能好等许多优点而被广泛应用于汽车、机床、铁路、矿山等各种机械设备中[1-2]。NP569484-NP644537圆锥滚子轴承是为某公司重点配套的产品,客户对轴承寿命有较高的要求,这就需要从设计、工艺上进行攻关。影响轴承寿命的因素很多,除了材料、热处理、制造加工、工装设备等,同轴承滚子-滚道凸型轮廓有很大的关系。进行凸度设计是减小应力集中、改善轴承寿命的一个重要手段。圆锥滚子轴承凸度设计包括凸型设计和凸度量设计[3],前者应尽量采用比较理想的凸型,而后者则取决于滚子载荷和长度。进行凸度设计,首先必须计算出滚子的最大接触载荷,而设计结果是否合理,还需要通过对滚子和滚道的接触应力进行仿真分析来加以衡量,直至确定合理的套圈和滚子凸度量。

1　工况条件分析

1.1工况条件

NP569484-NP644537轴承同时受径向力Fr和轴向力Fa的作用,需要对其极端工况进行分析。最恶劣的3种情形,如表1所示,其中α为轴承的接触角,ε为载荷分布系数,ϕ1为载荷角。极端的工况可能使轴承接触区域产生极大的应力,会加速轴承的疲劳破坏。对轴承滚子-滚道进行合理的凸度设计,可以减小这种的应力的影响。凸度量的大小可以通过仿真分析来判定其是否合理。

表1　3种恶劣工况条件以及载荷分布Tab.1 Working conditions and the load distribution

1.2工况分析

根据表1提供的数据,经过计算分析,这3种工况下,(Fr/Fa)tanα皆为0.8,ε皆为0.428 86,ϕl皆为81.818 2°。以第1种工况为例,计算结果为：接触滚子个数为11颗(为总数的1/2),最大滚子载荷为17.129 kN。具体结果参阅表2以及图1,其中D为轴承的外径,εD为载荷分布系数。

表2　第1种工况下轴承滚子-滚道载荷分布计算结果Tab.2 Load distribution calculation results of Roller-raceway

图1　轴承载荷分布示意图Fig.1 Schematic for load distribution

从上面的分析来看,本产品的设计特征是：外载荷的变化尽可能保持(Fr/Fa)tanα的数值为常数,以保证各种工况下轴承的载荷角为定值,即：各种工况条件下,轴承承载滚子个数恒定,为滚子总数的1/2。

2　轴承凸度匹配

通过以上工况条件分析,得到了轴承的载荷分布,选取最大的载荷Qmax作为设计载荷,进行凸度设计,并把凸度分配在滚子和套圈上,进行合理的匹配。设计原则是：① 轴承接触应力应远远小于产生永久变形时的接触应力4.0 GPa[4];② 轻载时滚子、滚道接触长度不小于滚子有效长度的70%,应有足够的承载长度;重载时不出现应力集中,防止轴承过早疲劳剥落[5]。

文献[6-7]中认为存在一种滚子轮廓可以产生印痕为矩形的压力分布,这种轮廓符合一个对数方程。以滚子为例,其形状如图2所示,由一段连续的特殊对数型曲线构成,图中a为曲线偏移量;滚道凸型与之类似。对数曲线方程见公式(1)。

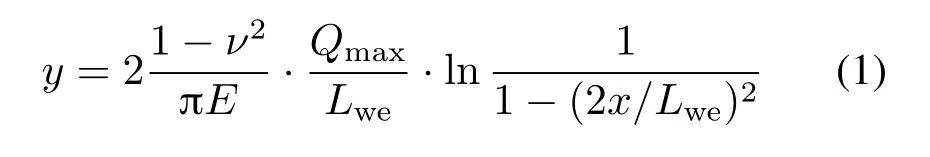
式中：ν为轴承材料泊松式;E为轴承材料弹性模量;Qmax为最大滚子载荷;Lwe为滚子的有效长度。

图2　对数母线滚子Fig.2 Logarithmic profile roller

测量点t1的凸度量δ按照下式计算：

式中：Rmax为滚子倒角最大尺寸;Lwe为滚子的有效长度;R为滚子两端弧坡的曲率半径;Dpw为滚子节圆直径;ϕ为滚子半锥角;Dwe为滚子平均直径。

将NP569484-NP644537轴承内、外圈以及滚子的凸度分为若干匹配等级,并在这几个等级中选取数种特征凸度匹配(见表3),进而对各种匹配关系进行有限元分析。

表3　凸度特征匹配Tab.3 Pressure of roller with logarithmic profile

3　应力分析

影响NP569484-NP644537轴承接触应力分布的结构参数和工况参数见表4。表中：Lwe为滚子的有效长度;Dw为滚子大头直径;Dwl为滚子小头直径;Dwe为滚子中心直径;Z为滚子个数;α为轴承公称接触角;ϕ为滚子半锥角;β=α-2ϕ;Qmax为最大滚子载荷;Dpw为滚子节圆直径。利用这些参数,可对轴承接触应力进行计算。

表4　NP569484-NP644537轴承的结构及工况参数Tab.4　The structure and operating conditions of bearings NP569484-NP644537

3.1理论计算

应用Hertz理论[7-8]的计算结果作为参考,以判断滚子-滚道接触应力状况。计算结果如下。

其中：dm为滚子-滚道接触区中点直径;为滚子与内滚道接触中心曲率和;h为滚子滚道接触半空;σmax为最大平均接触应力。

以上是以工况条件1为例,得到承受最大载荷的滚子接触尺寸以及平均应力分析情况。

3.2有限元分析

针对上面凸度匹配中的几个级别特征匹配,进行有限元分析,以得到较为合理的凸度配合。凸度设计采用对数凸型,凸度量大小按照表3中的方案。以下依据特征凸度匹配对各种情况进行有限元分析,有限元模型如图3所示。

图3　NP569484-NP644537圆锥滚子轴承有限元模型图Fig.3 Finite element model diagram of the tapered roller bearing NP569484-NP644537

模型建立依照以下原则进行。

(1)截取整个轴承的1/22,然后轴对称剖分为1/2,如图3(c)所示。

(2)以受力最大的的滚子-滚道为分析对象,即图1中编号为0的位置。

(3)建模过程中,单元选择solid brick 8node 185,单元剖分采用分层控制,在接触面上单元足够致密,非接触区域相对稀疏;相对接触区,各层按1：2.5递减,从而保证单元尺寸足够精细以控制计算精度和计算速度,保证单元完整并消除畸形单元以控制计算的收敛性。单元个数约为35 000个。从3.1节中的理论计算可知,有效接触长度为24.8 mm,接触面半宽大约0.21 mm,因而可在接触长度上设定300个节点,每个单元线性大小为mm=82.7µm＜b。

(4)外加约束条件：外圈固定,大端面横向施加约束,截面轴对称约束,并在内圈施加面载荷,大小为图1中编号为0处滚子载荷的1/2。

(5)计算方法为“惩罚函数法”,计算结果为von Mises应力。

3.2.1微凸型

参考表3,对各种凸型匹配予以分析,编号1-1～1-6微凸型分析情况如图4～9所示。其中, x=0.5Lx0,x0为凸型坐标。

图4　无凸型1-1应力分布Fig.4 Stress distribution for Non convex 1-1

图5　微凸型1-2应力分布Fig.5 Stress distribution for Micro convex 1-2

图6　微凸型1-3应力分布Fig.6 Stress distribution for Micro convex 1-3

图7　微凸型1-4应力分布Fig.7 Stress distribution for Micro convex 1-4

图8　微凸型1-5应力分布Fig.8 Stress distribution for Micro convex 1-5

图9　微凸型1-6应力分布Fig.9 Stress distribution for Micro convex 1-6

从图4中可以看出：无凸型情况下,滚子、滚道接触区域两端出现了严重的应力集中,最大von Mises应力达到3.103 GPa,可能会引起塑性变形。这种情况下,滚子、滚道需要有一定的凸度,以消除应力集中现象。

从图5中可以看出：接触应力最大的地方出现在接触区域中间部分,最大von Mises应力达到2.275 GPa;接触区域两端的应力变小,曲线变化趋势比较平坦,但是中间部分仍然比较大,可通过使滚道带凸度的办法予以改进。

从图6中可以看出：最大接触应力为2.144 GPa,出现在接触区域偏滚子大端的位置,而接触区域两端没有应力集中,变化也比较平缓;此种凸型较为合适。

图7是图6中的滚子、滚道轮廓曲线(见图1)的坐标原点沿着接触线向滚子大端偏移,但效果不好：在大端方向,内、外圈上出现了较大应力,最大达到2.346 GPa。

如图8所示,把图7中外圈小、内圈大的凸型改成相反的情况,内圈小、外圈大,结果应力分布状态较好。

但是,一旦将凸型的坐标函数偏移成图9情形,滚子小端方向的外圈滚道上出现最大应力,von Mises应力达到2.783 GPa;由于凸度偏移过大,滚子可能出现了一定的偏斜,引起了应力集中。

3.2.2中凸型

编号 2-1～2-5的中凸型应力分析情况如图10～14所示。

如图10所示,最大接触应力为2.260 GPa,出现在内圈中段,但整个接触区域应力值变化较大,外圈变化较缓。

图10　中凸型2-1应力分布Fig.10 Stress distribution for middle convex 2-1

加大内、外圈滚道凸度后,如图11所示,内圈应力变化趋势有所改善,但只增大到2.318 GPa;外圈应力变化平缓。这个凸型较为理想。

图11　中凸型2-2应力分布Fig.11 Stress distribution for middle convex 2-2

从图12中可以看到：最大接触应力为2.344 GPa,出现在内圈上,变化趋势过快;外圈变化较为平缓。这个凸型不太理想。

图12　中凸型2-3应力分布Fig.12 Stress distribution for middle convex 2-3

从图13中可以看出,最大应力2.310 GPa,没有应力集中,没有突变,应力变化较为理想。

图13　中凸型2-4应力分布Fig.13 Stress distribution for middle convex 2-4

从图14中可以看出：中凸型2-5的应力变化趋势较为平缓,可作为一种备用凸型。

图14　中凸型2-5应力分布Fig.14 Stress distribution for middle convex 2-5

3.2.3大凸型

编号 3-1～3-5的大凸型应力分析情况如图15～19所示。

图15　大凸型3-1应力分布Fig.15 Stress distribution for Large convex 3-1

图16　大凸型3-2应力分布Fig.16 Stress distribution for Large convex 3-2

图17　大凸型3-3应力分布图Fig.17 Stress distribution for Large convex 3-3

图18　大凸型3-4应力分布图Fig.18 Stress distribution for Large convex 3-4

图19　大凸型3-5应力分布Fig.19 Stress distribution for Large convex 3-5

加大轴承滚子-滚道的凸度,如图15中大凸型3-1,其应力变化较图16好,可采用。

从图16、图17可以看出,应力水平和接触长度都能满足条件,两类图形均可采用。

图18中可以看出,大凸型3-4应力分布图平缓且最大接触应力为2.312 GPa,可以采用。

图19中的最大接触应力为2.285 GPa,内外圈接触应力也较为接近;接触长度有所减小,但满足不小于70%有效接触长度的条件,也可以作为备用凸型。

3.3讨论

本例的凸度选取是以轴承滚子-滚道接触应力的平缓程度、有无应力集中,以及内、外圈应力大小情况为准的。由于是重载,接触长度不予考虑;实际上,由于本例的载荷已经接近0.5倍的额定动载荷,只要凸度不是过大,必然能够保证接触长度。

表5　较为理想的凸型选取Tab.5 Convex type selection

从以上有限元分析中可以看出：微凸型1-3、1-5可以采用;中凸型2-2、2-4、2-5可以采用;大凸型5种皆可采用。考虑到轴承磨合阶段的磨损,不宜采用小凸度;实际上,在以上的分析中,可以看到,较为理想的凸型大部分都落在中凸型和大凸型区域,尤其是大凸型,选取的几种凸型几乎全部适合,说明选取的大凸型应是较为理想的。因而可以在中凸型和大凸型中选取较理想的凸度匹配,如表5所示。

4　结论

经过以上分析,可以得出结论：内圈凸度量14～30µm为宜,外圈凸度量14～28µm为宜。

“沟道控制理论”[9]要求外圈不宜有大的凸度量,滚子在过大的凸度量下,尤其是外圈凸度量过大时,容易产生滑动以及过大的陀螺力矩;因此,建议外圈凸度量尽量向小取。

本文虽然在理论分析上有了一些成果,但是由于时间和条件的限制,还有以下几方面有待进一步研究：

(1)在非零游隙的情况下,同时考虑承受轴向力、径向力以及力矩的联合载荷作用,计算轴承载荷分布以及接触应力水平。

(2)目前,等应力设计[10]的概念已经提出,其要求轴承内、外圈的接触应力相等或者近似相等,但此技术尚未在圆锥滚子轴承上推广,只有更进一步地研究滚子、滚道的凸度匹配方式,才能使轴承的内、外圈疲劳失效发生在同一时间。

[1]吴飞科.圆锥滚子轴承接触应力分析与凸度设计[D].洛阳：河南科技大学,2007.

[2]王志伟.圆锥滚子轴承滚子凸度的优化设计[J].机械设计与制造,2014(6)：55-61.

[3]马芳,李海涛.圆锥滚子轴承滚子凸度设计[J].哈尔滨轴承,2014,6(35)：1-4.

[4]GB/T 4662—2003/ISO 76：1987.滚动轴承额定静载荷[S].滚动轴承标准化技术委员会.

[5]孙立明,王大力.汽车轮毂轴承凸度有限元分析[J].轴承,2005(2)：1-3.

[6]LUNDBERG G.Elastic contact between two semi-infinite bodies[J].Fur schung auf dem Gebiete des Engenieurwesens,1961(5)：21—24.

[7]HARRIS T A.Rolling bearing analysis[M].3rd,ed.New York：John Wiley&sons,Inc,1991.

[8]罗继伟,罗天宇.滚动轴承分析计算与应用[M].北京：机械工业出版社,2009：14-18.

[9]赵春江.高速滚珠轴承动态特性求解的沟道控制理论修正[J].农业机械学报,2009,40(5)：199-202.

[10]孙北奇.球轴承等应力设计中沟曲率系数的求解[J].轴承,2009(5)：11-13.

Finite Element Analysis on Contact Stress of the Roller-Raceway for Tapered Roller Bearings NP569484-NP644537

WU Fei-ke,LIU Sai,YAN Jian-gang,YANG Guo-ce,SONG Yu-lei
(Engineering Training Center,Shanghai Second Polytechnic University,Shanghai 201209,P.R.China)

The crowning design of tapered roller bearing includes the profile design and the convex metric design.Based on the general logarithmically convex type,the distribution of convex metric on the roller-raceway is a subject to be studied in the future.Through the calculation of particular condition for the level of roller-raceway contact stress,the design rationality is evaluated.The tapered roller bearings NP569484-NP644537 as an example,using the orthogonal groups method,matching several level classification for the roller-raceway of sampling bearing to select feature matching,the finite element analysis is done for feature matching.The contact stress should meet the engineering conditions meanwhile ensure the sufficient contact length is ensured.

tapered roller bearing;load distribution;contact stress;crowning design;orthogonal method;finite element analysis

TH123

A

1001-4543(2015)04-0303-09

2015-01-23

吴飞科(1981—),男,河南省汝阳县人,工程师,硕士,主要研究方向为机械设计及理论。电子邮箱fkwu@sspu.edu.cn。

2015年度上海第二工业大学校基金(No.A01GY15GX58)资助