基于DFT MMSE的OFDM 16QAM调制系统信道估计算法

龚玉梅,胡金艳,方安乐,邵宇丰

(上海第二工业大学计算机与信息工程学院,上海201209)

基于DFT MMSE的OFDM 16QAM调制系统信道估计算法

龚玉梅,胡金艳,方安乐,邵宇丰

(上海第二工业大学计算机与信息工程学院,上海201209)

正交频分复用(OFDM)技术具有较强的抗多径衰落能力与很高的频谱利用率,被广泛应用于无线通信领域。高效精确的信道估计是OFDM系统的关键技术之一,影响系统传输性能。针对16QAM OFDM无线传输系统,提出基于离散傅里叶变化(DFT)的最小均方误差(MMSE)算法,进行Matlab建模与仿真。结果表明,相对传统信道估计方法,拟合信道频率响应曲线更接近于真实信道;较传统最小平方(LS)算法,系统接收端误码率有很大改善,在恶劣噪声信道中,误码率降低一个数量级,有效提高了无线OFDM系统的传输性能。

正交频分复用;信道估计;离散傅里叶变化最小均方误差算法

0　引言

在多径衰落无线传输信道上,高速数据传输中会产生严重的码间串扰,正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)是多载波并行调制的一种,将高速串行数据码流转换成低速并行数据码流进行传输。它具有优良的抗多径衰落能力,能够有效改善高速传输时码元信号间干扰,同时由于其子载波正交的特点,提高了频谱利用率,增大了系统传输带宽[1-2]。

在OFDM系统中,信号经过编码调制与相应变化,通过无线信道发射,由于无线信号传输路径的复杂性与时变性,接收端的信号因受到信道特性的影响而产生失真,所以在接收机端需要对信道的影响进行估计和补偿。信道估计的准确性与高效性将直接影响整个OFDM通信系统的传输性能[3-4]。

常用的信道估计算法有最小平方(Least Square, LS)估计算法、最小均方误差 (Minimum Mean Square Error,MMSE)估计算法等[5-6]。本文利用离散傅里叶变换(Discrete Fourier Transform,DFT)将MMSE频域估计与时域去噪相结合,减低带外噪声的影响,针对16QAM OFDM无线通信系统进行系统建模与算法仿真,并根据仿真结果对DFT MMSE信道估计方法进行性能评估。

1 无线OFDM系统模型

OFDM技术是一种多信道传输方式,采用多个载波对信号进行调制,降低每个载波的调制码元速率与信道带宽,克服码间串扰。各路子载波的频谱有一定的重叠,但已调信号在一个码元持续时间内正交,充分利用了频带宽度,被广泛地应用于无线数字通信系统中[7]。

假设一个OFDM系统中有N个子信道,子信道中信号码元为Bk,fk为第k路子载波的频率,ϕk为第k路子载波的初始相位,则在此系统中N路子信号之和可以表示为

在码元持续时间TB内任意两个子载波正交条件为

即子载波频率满足fk=k/(2TB)。

在实际应用中,发送端采用傅里叶逆变换(Inverse Discrete Fourier Transform,IDFT)实现OFDM调制,接收端采用DFT实现OFDM信号的解调。无线信道产生的多径效应会导致符号干扰(InterSymbol Interference,ISI)与子载波干扰(InterCarrier Interference,ICI),因此需要在调制信号后插入保护间隔循环前缀(Cyclic Prefix,CP),一般要求保护间隔长度TG大于无线信道的最大扩展延迟Tm。

无线OFDM系统原理如图1所示,数据源经过源编码、信道交织编码等,进行串并转换划分多个子载波,通过IDFT实现OFDM信号的调制,并插入CP减少ISI与ICI,再经过D/A与上变频后转变成可传输的无线信号,通过无线信道到达接收端。在接收端,对接收信号进行下变频,去除CP,得到OFDM已调抽样序列,对该序列做DFT,从而得到源调制信息序列。

图1　无线OFDM系统原理方块图Fig.1 Block diagram of wireless OFDM system

2　信道估计模型与算法

2.1信道估计的基本模型

信道估计基本模型如图2所示,发送信号经信道到达接收端,通过合适的信道估计模型,使得信道估计后得到的信号与实际接收信号间的误差减小。

图2　信道估计模型Fig.2 Channel estimation model

OFDM发射信号在时域可以表示为

通过L条路径的无线通道后,接收端信号为

信道估计就是为了得到发射天线到接收天线之间的信道频率响应,从而在接收端对信号进行预补偿,降低误码率,提高接收性能。

目前常用的信道估计方法主要为基于导频或训练序列的信道估计、盲信道估计。基于导频或训练序列的信道估计方法通过在发送端发送一定的已知导频符号或训练序列,经过信道传输后到达接收端,根据接收信号与发送信号进行信道估计。导频结构可以分为3种：块状导频、梳妆导频和格状导频。块状导频是以一定的时间间隔,在OFDM信号的所有子载波信道上插入导频信号;梳妆导频是在OFDM信号子载波上以一定的频率间隔插入导频信号;格状导频则沿时间和频率两个方向插入导频。盲信道估计利用接收信号自身的统计特性,无需插入导频或训练序列,提高了系统传输效率,但需要大量的接收数据存储与处理,效果低于导频估计方式,且不适用于快变通道[8-9]。

常用的信道估计性能评估方法有以下几种：(1)估计信道的频率响应曲线与实际信道响应进行拟合对比,去除噪声的理想信道频率响应可以表示为H=Y X-1,其中Y与X分别为接收端与发射端的频域表示;(2)系统传输误码率,是指二进制码元在数据传输系统中被传错的概率,Pe=Ne/N,N为传输的二进制码元的总数,Ne为传错的码元总数; (3)传输星座图,将数字信号在复平面上表示,以直观地表示信号以及信号之间的关系。

2.2DFT MMSE算法模型

信道估计算法主要有LS算法和MMSE算法。MMSE估计的原理是通过求得一个合适的信道冲击响应(Channel Impulse Response,CIR),使得通过补偿和校正后得到的接收数据与发送端源数据的误差均方和最小。

其中：RHY为信道响应与接收信号的互相关矩阵; RYY为接收信号的自相关矩阵。

DFT MMSE算法根据信道时域能量比较集中的特点,在时域内保留多径内的信号能量,其余部分置零处理,减低了噪声的影响,提高了MMSE信道估计的性能,原理框图如图3所示。

图3　DFT MMSE估计方法Fig.3 DFT MMSE estimation algorithm

再进行N点DFT到频域,

3　实验仿真结果

通过Matlab仿真建模,以16QAM调制OFDM系统为仿真模型,采用梳妆导频线性插值方式,对传统的LS算法、MMSE算法以及DFT MMSE算法进行信道估计效果与误码率的比较分析。其中,OFDM信号子载波数为32,随机产生频域信道,比较算法估计信道响应与实际信道特性的差别。图4为不同算法信道拟合曲线,可以看出DFT MMSE算法相比较LS算法与传统MMSE算法,估计信道频域响应曲线更接近实际信道特性。

同时,对不同信噪比(SignaltoNoiseRatio,SNR)下的误码率(Bit Error Rate,BER)进行了比较,仿真结果如图5所示。由图5可见,当传输信号信噪比处于20～70 dB的范围内时,DFT MMSE相较于其他两种传统算法,在误码率上有很大的降低,且其改善作用与发射端信噪比相关性不大,具有较宽广的应用范围,有利于提高系统的传输性能。信道估计前后的接收端星座图如图6所示,表明在使用DFTMMSE信道估计算法后,星座图清晰收敛,相邻星座点间干扰较小,形象地展示了该方法对通信系统传输性能的改善作用。

图4　估计信道频域响应曲线Fig.4 Estimated channel frequency response curves

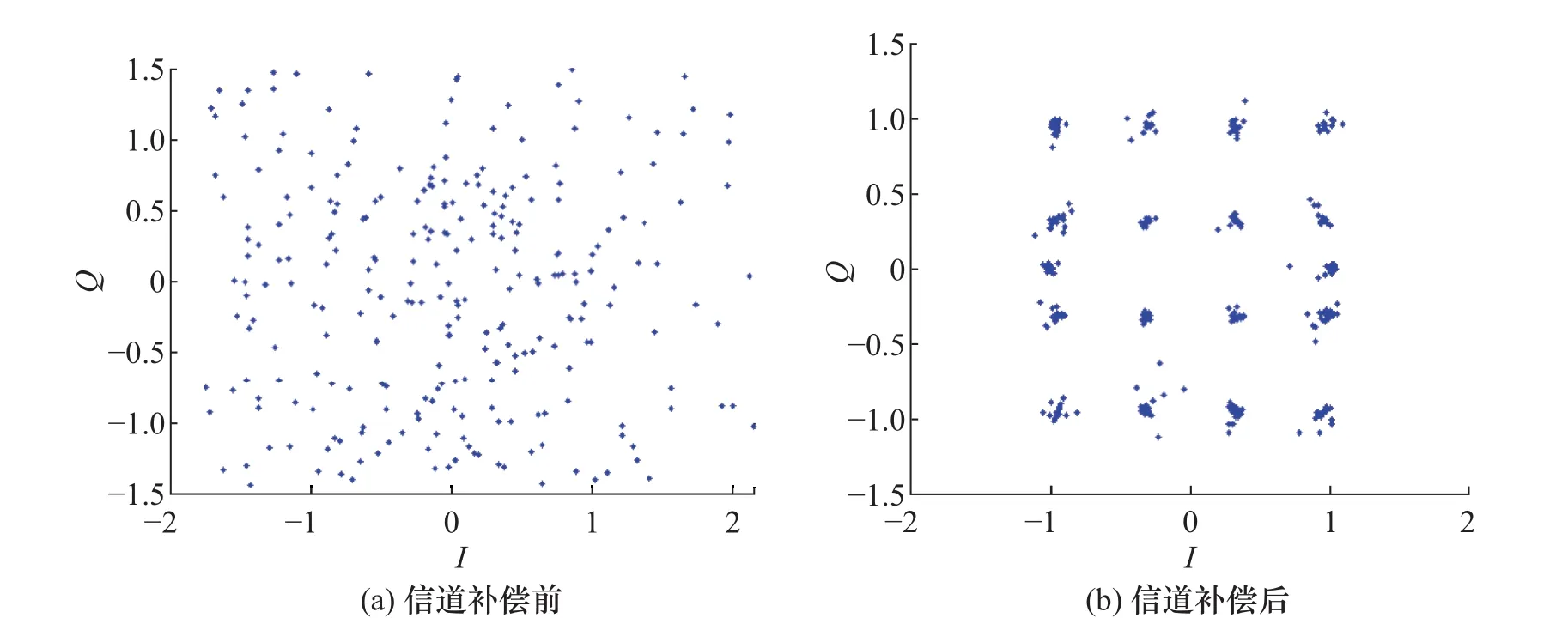
图6　信道补偿前后星座图Fig.6 Constellation diagrams before/after channel estimation

4　结论

通过理论与仿真分析表明,基于DFT MMSE的信道估计方法是一种在最长传输时延可估计的16QAM调制OFDM通信系统中,以随机信道为传输链路,相比较于传统的信道估计算法,具有更好的信道估计性能,估计结果更接近实际信道,系统的传输误码率降低的方法。DFT MMSE算法通过IDFT与DFT的快速转换运算,剔除传输时域外噪声的干扰,实现了时域与频域的联合处理,提高了系统性能,同时具备一定的工程应用前景。

[1]NEE R V,PRASAD R.OFDM for wireless multimedia communications[M].Boston：Artech House,2000.

[2]樊昌信,曹丽娜.通信原理[M].7版.北京：国防工业出版社,2012.

[3]COLERI S,ERGEN M,PURI A,et al.Channel estimation techniques based on pilot arrangement in OFDM systems [J].IEEE Tran Broadcast,2002,48(3)：223-229.

[4]ZHANG P L,ZHANG H X,LIU H D,et al.Particle filtering based channel estimation in OFDM power line communication[J].The Journal of China Universities of Posts and Telecommunications,2014(05)：24-30.

[5]张帅,白成林,罗清龙,等.相干光OFDM系统中MMSE信道估计研究[J].光电子·激光,2013(03)：508-513.

[6]SU W,PAN Z.Iterative LS channel estimation for OFDM systems based on transform-domain processing [C]//International Conference on Wireless Communica-tions,Networking&Mobile Computing.Shanghai：IEEE Conference,2007.

[7]啜钢,王文博,常永宇,等.移动通信原理与系统[M].北京：北京邮电大学出版社,2005.

[8]LI M,TAN J,ZHANG W.Channel estimation method based on frequency-domain pilots and time-domain processing for of DM systems[J].IEEE Trans on Consumer Electronics,2004,50(4)：1049-1057.

[9]WANG N,DENG P.Interpolation in OFDM channel estimation based on pilot arrangement[J].成都信息工程学院学报,2008,23(2)：141-146.

A DFT MMSE Channel Estimation Algorithm for 16-QAM OFDM Wireless System

GONG Yu-mei,HU Jin-yan,FANG An-le,SHAO Yu-feng
(School of Computer and Information Engineering,Shanghai Second Polytechnic University, Shanghai 201209,P.R.China)

Orthogonal frequency division multiplexing(OFDM)has strong anti-multipath fading ability and high frequency spectrum utilization,which has been widely adopted in wireless communication field.Accurate and efficient channel estimation algorithm is one of the key technologies in OFDM system,which highly impacts the overall system performance.A discrete fourier transform(DFT)-based minimum mean square error(MMSE)algorithm is proposed for a 16-QAM(quadrature amplitude modulation)OFDM wireless communicationsystemandsimulatedbyusingMatlab.Thesimulationresultsdemonstratethattheestimatedchannelfrequencyresponse is more close to the real channel frequency response comparing to the traditional algorithm.DFT MMSE has a better performance on bit error rate(BER)than least-square(LS)algorithm,especially on low signal-to-noise ratio(SNR)circumstance.

OrthogonalFrequencyMultiplexing(OFDM);channelestimation;DiscreteFourierTransformMinimumMeanSquareError (DFT MMSE)

TN911

A

1001-4543(2015)04-0331-05

2015-05-21

龚玉梅(1984—),女,安徽人,讲师,博士,主要研究方向为通信与信息系统。电子邮箱ymgong@sspu.edu.cn。

上海第二工业大学校基金(No.EGD15XQD06)、上海高校青年教师培养资助计划(No.ZZZZEGD15003)资助