一种改进的多目标量子免疫克隆算法

叶燕杰，胡震云，b，c，陈志明

(河海大学 a.商学院;b.水文水资源与水利工程科学国家重点实验室;c.管理科学研究所，南京 210098)

自20世纪80年代开始，进化算法逐步发展成为能有效解决多目标优化问题的重要方法。1985年出现的基于向量评估的VEGA算法［1］是第一个多目标算法，但本质上VEGA算法仍然是加权和方法。现代智能的多目标优化算法源于20世纪90年代之后，由于计算机的普及，通过机器学习，进化算法的并行性得到广泛的利用，相继出现了由Deb等提出的非支配排序遗传算法(NSGA)［2］，Zitzler和 Thiele 提出的强度 Pareto 进化算法(SPEA)［3］，Horn 和 Nafpliotis提出的基于小生境的 Pareto遗传算法(NPGA)，Fonseca和Fleming提出的多目标遗传算法(MOGA)。这些算法为今后的多目标优化方法研究打下了坚实的基础。国内学者对多目标问题进行了大量有价值的研究，吴勇等［4］将NSGA-Ⅱ用于催化裂化加工装置优化设计中，并引入多目标综合评价优化函数。张宇献等［5］将免疫遗传算法框架与量子计算思想相结合，并提出基于量子位实数编码的热连轧轧制规程多目标优化算法，均取得了良好的效果。

量子免疫克隆算法(quantum-inspired immune clone algorithm，QICA)是一种新颖的智能优化算法，由李阳阳和焦李成于2005年提出［6］。量子免疫克隆算法结合量子搜索机制和人工免疫系统的克隆选择原理，利用量子编码的叠加性和随机性构造抗体;利用克隆操作产生克隆种群从而实现种群扩张，提高了局部搜索能力;采用通用的量子门旋转操作，同时引入旋转角度动态调整机制和量子交叉策略［7］。李阳阳等［8］结合免疫系统的免疫优势理论和抗体克隆选择学说，提出了量子免疫克隆多目标优化算法。对于量子免疫克隆算法的改进，文献［9］采用量子旋转门进行演进，同时借助全干扰交叉操作，避免陷入局部最优;文献［10］提出一种基于实数编码的量子免疫克隆算法，算法利用量子位的概率幅直接编码，并对旋转角度和角度大小进行改进。杜振华等［11］提出了免疫克隆选择多目标优化算法，该算法通过变异算子实现对优异抗体的克隆。

量子免疫克隆算法在组合优化问题中有良好的表现，但在多目标优化领域的研究却较为少见，且QICA算法的编码复杂，计算精度受编码位数限制，需要进行频繁的编、解码操作，增加了算法的计算量，降低了算法效率和寻优速度。本文在量子免疫克隆多目标优化算法的基础上提出了一种改进的量子免疫克隆多目标优化算法(improved multi-objective quantum-inspired immune clone algorithm，IMOQICA)。该算法将快速非支配排序策略应用于QICA，从而降低了算法的复杂度;提出一种改进的克隆规模计算方式，从而有效地增大优良个体的比例，减少不良个体的影响;在确定量子旋转角度大小方面，提出了改进的混沌旋转角度策略，加速了算法收敛;并对锦标赛选择的规则进行了改进，提高了算法的搜索效率。

1 改进的多目标量子免疫克隆算法

1.1 算法流程

改进的多目标量子免疫克隆算法流程见图1。

1.2 算法实施步骤

步骤1 设置进化代数计数器t=1，通过量子计算生成含有2m个抗体的初始种群Q(t)(t=0);

步骤2 量子态观测，将量子抗体观测成二进制抗体P(t);

步骤3 分别计算每个抗体对应的亲和度值、抗体浓度和拥挤距离;

步骤4 根据亲和度、拥挤距离及抗体浓度的大小自适应调整的克隆规模进行克隆扩增，得到新的量子种群Qclone(t);

步骤5 将克隆后的量子抗体Qclone(t)进行量子旋转门变异操作，得到新的量子种群Qclone.rotation(t);

步骤6 重新测量Qclone.rotation(t)，得到二进制编码Pclone.rotation(t)，并计算适应度值;

步骤7 判断序值分类和拥挤距离计算是否完成，若完成则转到步骤10;否则，转步骤8;

步骤8 快速非支配排序;

步骤9 计算同一非劣等级中抗体的拥挤密度;

步骤10 锦标赛选择;

步骤11 采用自适应交叉、变异等操作，形成种群Qt;

步骤12 将Pt和Qt合并成新种群Nt;

步骤13 计算新种群Nt中各抗体对应的亲和度值;

步骤14 采取与步骤3相同的方法，对新种群Nt进行非支配排序;选取前N个抗体产生新的种群NPt，并同时更新免疫记忆细胞;

步骤15 进化终止条件判定。若已经达到最大迭代次数，运算结束并输入计算结果;否则，进行下一次迭代，转步骤3。

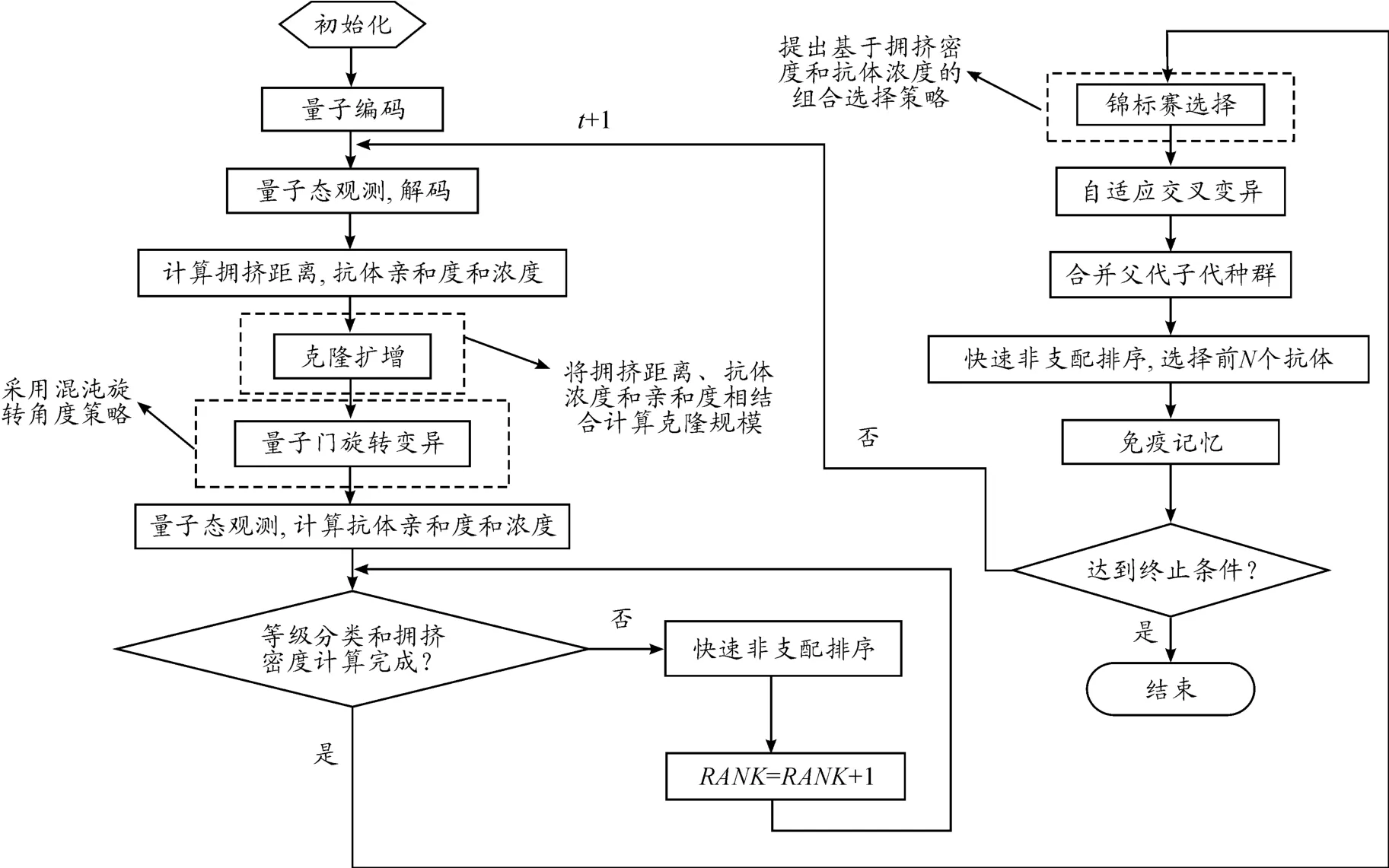
图1 改进的IMOQICA算法流程

1.3 量子免疫克隆算子设计

1)改进的克隆规模算子

其中:Nc为与克隆规模相关的设定值，且满足Nc＞n;F(x)为亲和度函数;idistance为拥挤距离;idensity为抗体浓度;⎿x」为小于x的最大整数;α，β为常量，且α，β＞0。由此可见:对于单一抗体而言，其克隆规模是依据抗体适应度、拥挤距离和抗体浓度自适应地调整。具体来讲，抗体适应度越大、拥挤距离越大、抗体浓度越小，其克隆规模越大，被搜索的机会就越多。

2)改进的混沌量子旋转角

抗体的变异操作能够提高算法的搜索能力，而变异策略多种多样。文献［12］使用在指导量子染色体的周围随机散布量子染色体的方式进行变异操作;文献［10］采用最常见的量子旋转门操作，量子旋转门的角度通过查表得到。文献［9］采用的量子旋转门如下:

其中:θ为旋转角度，一般地，θ∈(0.005π，0.1π)，量子门旋转角度的大小直接影响算法的收敛速度。

本文采用混沌系统的原理来确定旋转角度的大小。混沌是非线性系统的本质特征，它是一种自然界普遍存在的非线性现象，具有随机性、遍历性、规律性等特殊性质。在混沌优化中，对于产生混沌变量的系统一般选用 Logistic映射［13］，即虫口模型，是指在确定的地域范围内昆虫数目随着时间变化的一种数学模型，表示如下:

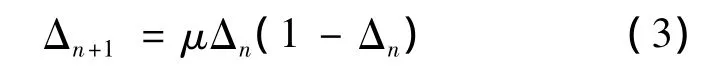
其中:μ是混沌吸引子，一般地，当μ=4时，系统进入混沌状态，产生混沌变量 Δn(n=1，2，…)，且Δn∈［0，1］。为此，本文将量子旋转角度大小定义为

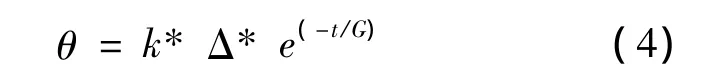
其中:k为调节因子，本文设定 k∈［0.01π，0.15π］;Δ通过式(3)获得;t为当前进化代数。

3)改进的锦标赛选择策略

传统的锦标赛选择，其实质是在选择时首先基于快速非支配排序策略，比较两抗体的非劣前沿等级，取等级较低的抗体，否则在同一等级中取拥挤距离较大者作为选择的对象。参数k为联赛规模，一般取k=2。显然，这种选择方式也使得拥挤距离较大的抗体具有较大的“生存”机会。但是仅考虑拥挤距离出现过早收敛和停滞等现象，不利于抗体的多样性，因而本文提出了基于拥挤密度和抗体浓度的组合赋权选择策略，具体步骤如下:

步骤1 首先选择2个个体，比较其非劣前沿等级，若非劣等级不同，则取等级级数较低的个体;否则转步骤2;

步骤2 若2个个体在同一非劣等级，则按照以下公式进行选择:

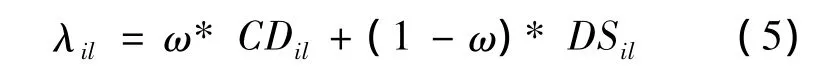
其中:CDil和DSil分别为在级别l中抗体qi的拥挤密度和抗体浓度;本文将ω定义为锦标赛选择系数，且ω＞0;λil为抗体qi的组合选择值。从表达式中可以看出:拥挤密度越小、抗体浓度越小，综合选择值也越小，因而选择概率越大，故在同一级别中，综合选择值越小的抗体排序越靠前。

2 算法性能测试

2.1 参数设置和性能指标

为了说明算法的优越性，将其与多目标算法NSGA-II进行比较。相关参数设置如下:

对NSGA-II算法，设定最大迭代次数为200，种群规模为100，适应度函数值偏差为1e-100;采用模拟二元交叉和多项式变异策略，设置交叉概率pc=0.8，变异概率pm=1/n，模拟二元交叉的分布指数为15，多项式变异的分布指数为20。

对改进的多目标量子免疫克隆算法(IMOQICA)，设定最大迭代次数为200，种群规模为100，克隆规模为50，锦标赛选择规模为2，人工免疫记忆库规模为50，适应度函数值偏差为1e-100;采用自适应交叉和变异策略，设置交叉概率pc∈［0.4，0.99］，变异概率 pm∈［0.000 1，0.1］［14］。

由于多目标优化问题存在一系列的Pareto-最优解，故目前对于多目标算法还没有统一的性能评价准则。一般来说，多目标优化算法的最优解集与理想最优Pareto-前端的距离越小越好，解分布越均匀越好，算法收敛性越大越好。本文选取4个性能度量指标定量地评价算法的性能，分别为算法平均运行时间(AVGTime)、算法收敛性(convergence capability)、两个解集之间的覆盖率(converage of two sets，CS)［15］和均匀性度量方法中的空间度量指标——分布度(spacing，SP)［16］。

2.2 测试函数

为了验证改进的多目标量子免疫克隆算法在解决多目标优化问题上的有效性，本文选取3维目标测试函数 MOP5、经典 kur测试函数以及DTLZ2测试函数，测试函数如下所示:

1)MOP5测试函数，该测试函数是2维3目标优化问题。

2)kur测试函数，该函数问题是3维2目标问题，且其Pareto最优前沿面是不连续的。

3)DTLZ2测试函数，该函数为3维目标问题，特征是高维目标函数空间，且其最优Pareto-前端满足，即第一象限内的单位球面。

2.3 算法性能对比

2.3.1 解集分布图对比

通过对图2～4这3种不同类型的测试函数的Pareto解集分布图的性能对比，可以看出采用改进的多目标量子免疫克隆算法所得的Pareto解集具有优良的多样性，尤其是种群收敛的稳定性大幅提升，具有更快的全局寻优能力，能有效地防止种群退化。

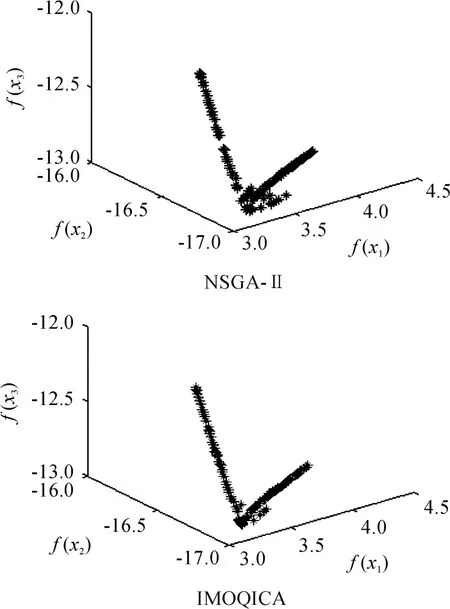
图2 测试函数1的解集分布图

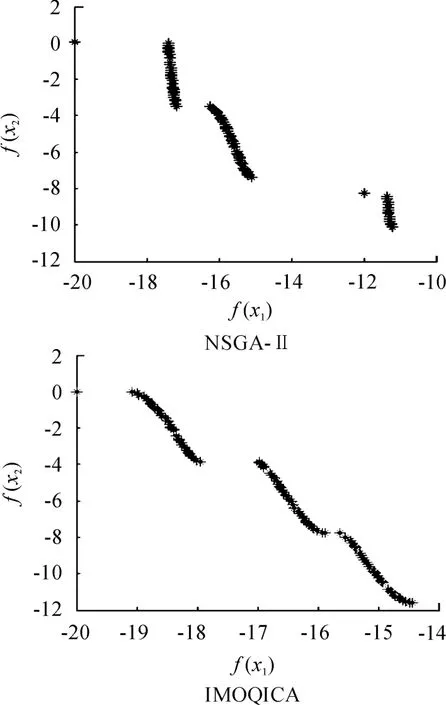
图3 测试函数2的解集分布图

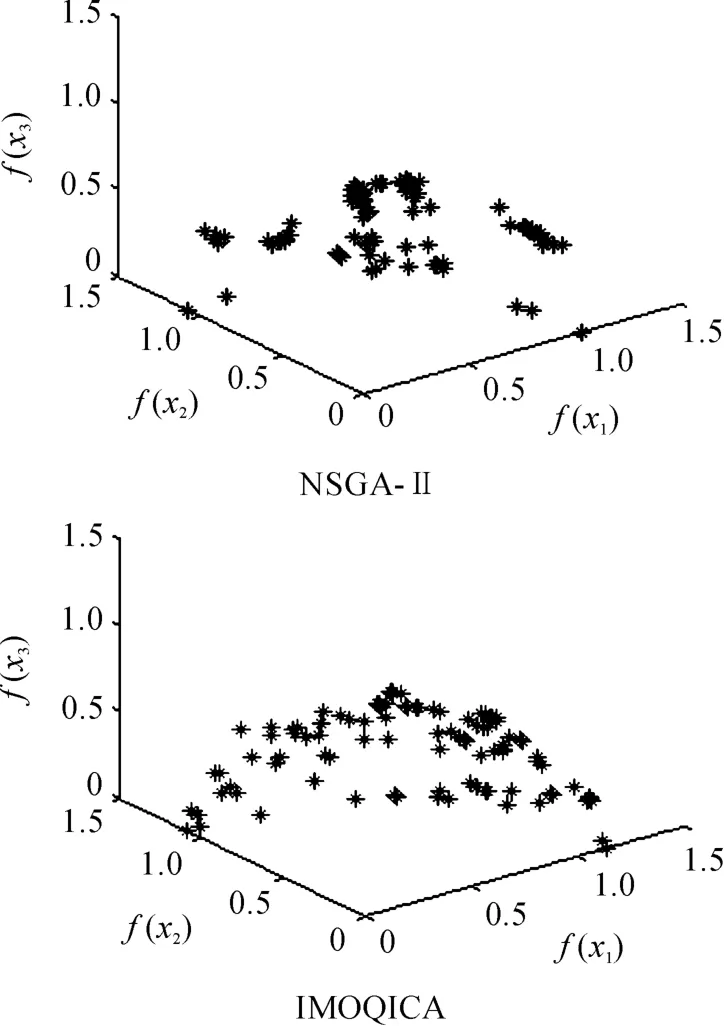
图4 测试函数3的解集分布图

2.3.2 指标性能对比

本文提出4个衡量算法性能的指标，分别是算法平均运行时间(AVGTime)、算法收敛性(convergence capability)、两个解集之间的覆盖率(converage of two sets，CS)［15］和均匀性度量方法中的空间度量指标——分布度(spacing，SP)［16］。

1)算法平均运行时间和算法收敛性。从表1中的指标可以看出:IMOQICA算法较NSGA-II算法在平均运行时间和算法收敛性上都有较大提高。特别是在三维目标问题上，IMOQICA算法收敛能力更强、收敛速度更快，具有更好、更快的全局搜索能力，能够有效防止种群退化，这使得其能够有效地解决高维、多目标优化问题。

2)两个解集之间的覆盖率。表2指标S由4个子指标来衡量，分别是Min、Mean、Max以及Std。从4个指标来看，IMOQICA均优于NSGA。特别是Std，它反映解的波动性大小，IMOQICA算法的波动性远小于NSGA，说明本文算法解集分布更加均匀，这也与上图结果相吻合。

3)分布度。从表3中的指标可以看出，对于3种不同的测试函数，ζ(XI，XN)均要明显大于ζ(XN，XI)，由此可说明IMOQICA算法寻找到的最优解在很大程度上支配着NSGA-II算法找到的最优解，表明算法具有较强的搜索寻优能力。

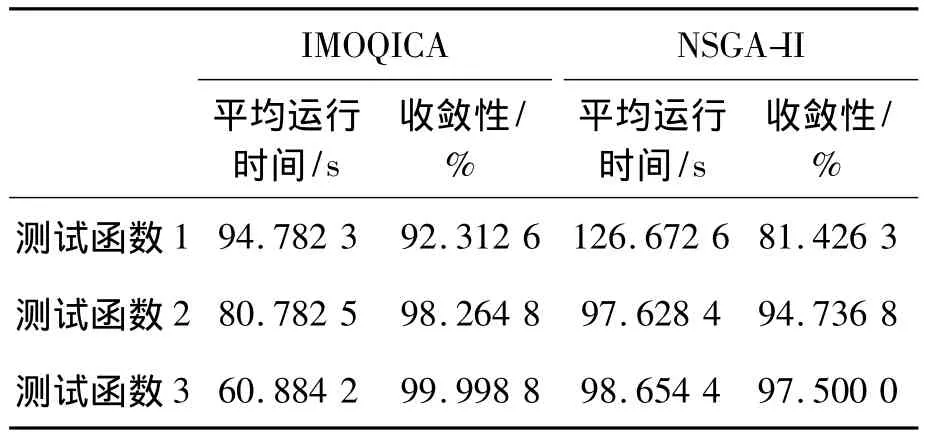
表1 两种算法在3种不同测试函数下的全局搜索能力比对

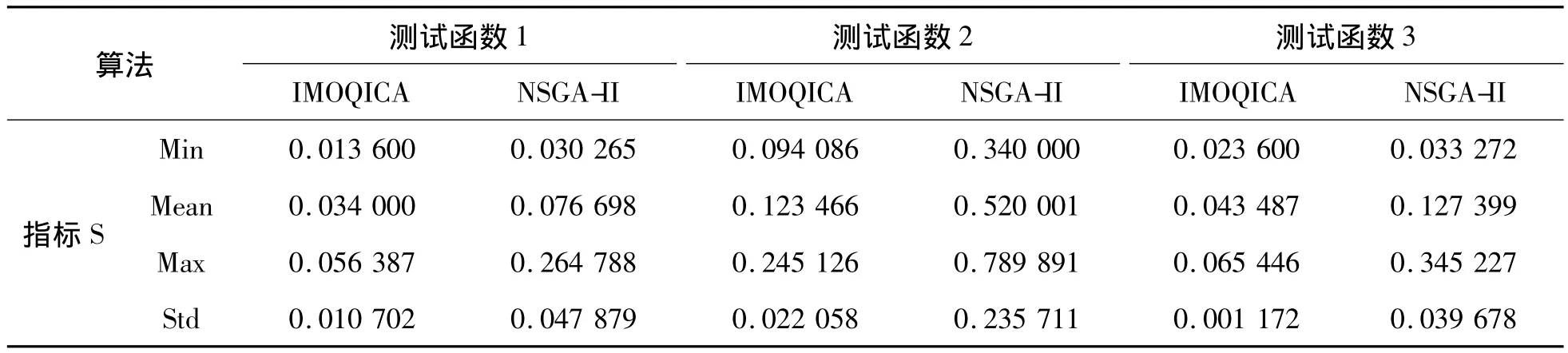
表2 性能评价指标Spacing的测试结果

表3 性能评价指标S测度的测试结果

3 结束语

针对量子免疫克隆算法在解决多目标优化问题时存在编码复杂、需要频繁的解编码操作以及计算量较大等缺陷，本文提出了一种改进的多目标量子免疫克隆算法。算法中，克隆规模大小由抗体适应度、拥挤距离和抗体浓度共同决定，采用混沌系统的原理来确定旋转角度的大小，且采用了改进的锦标赛选择模式。通过3个典型多目标函数优化问题的性能测试结果表明:与NSGA-II算法相比较，该算法更适用于解决多目标优化问题，并且收敛速度快，程序运行时间大大缩短，具有较强的全局搜索能力。

［1］SCHAFFER J D.Multiple objective optimization with vector evaluated genetic algorithms［C］//In the Proceedings of the International Conference on Genetic Algorithms and Their Applications，Pittsburgh.PA:［s.n.］，1985:93-100.

［2］SRINIVAS N，DEB K.Multi-objective optimization using non-dominated in genetic algorithms［J］.Evolutionary Computation，1994，2(3):221-248.

［3］ZITZLER E，THIELE L.Multiobjective Evolutionary Algorithms:A Comparative Case Study and the Strength Pareto Approach［J］.IEEE Transaction on Evolutionary Computation，1999(3):257-271.

［4］吴勇，程明，项敏建.基于NSGA-Ⅱ的催化裂化分馏塔的多目标优化［J］.计算机测量与控制，2015(1):70-72.

［5］张宇献，李松，李勇，等.基于量子位实数编码的优化算法及轧制规程多目标优化［J］.仪器仪表学报，2014(11):2440-2447.

［6］JIAO LICHENG，LI YANGYANG.Quantum-inspired Immune Clonal Optimization［C］//Proc.of International Conference on Neural Networks and Brain.Beijing，China:［s.n.］，2005:461-466.

［7］祁浩，王福豹，邓宏，等.基于量子免疫克隆算法的神经网络优化方法［J］.计算机应用，2014(2):496-500.

［8］李阳阳，焦李成.量子免疫克隆多目标优化算法［J］.电子与信息学报，2008(6):1367-1371.

［9］JIAO LICHENG，LI YANGYANG，GONG MAOGUO，et al.Quantum-imspired Immune Clonal Algorithm for Global Optimization［J］.IEEE Transactions on Systems，Man and Cybernetics，Part B:Cybernetics，2008，38(10):1234-1253.

［10］王娟，李飞.一种基于实数编码的量子免疫克隆算法［J］.计算机工程，2012，18:133-136.

［11］杜振华，闫肃，谌海云，等.免疫克隆选择多目标优化算法与MATLAB实现［J］.智能计算机与应用，2014(3):45-48.

［12］於时才，马宁，亢军贤.基于免疫克隆选择算法的神经网络规则抽取［J］.计算机工程，2009，35(1):173-175.

［13］韩春艳，禹思敏.改进的Logistic映射及其动力学特性［J］.中国海洋大学学报:自然科学版，2015(5):120-125.

［14］邓富民，梁学栋，刘爱军，等.多资源约束下改进NSGA-Ⅱ算法的手术调度［J］.系统工程理论与实践，2012，32(6):1337-1345.

［15］ZITZLER E，DEB K，THIELE L.Comparison of Multiobjective Evolutionary Algorithms:Empirical Results［J］.Evolutionary Computation，2000，8(2):173-195.

［16］SCHOTT J R.Fault Tolerant Design Using Single and Multicriteria Genetic Algorithm Optimization［D］.Cambridge:Massachusetts Institute of Technology，1995.