采用刚柔耦合模型的轿车平顺性仿真分析及优化

王 滕，欧 健，张 勇，杨鄂川，邓国红

(重庆理工大学 a.车辆工程学院;b.机械工程学院，重庆 400054)

随着汽车的普及，人们对汽车整体性能的要求也越来越高，而平顺性作为汽车的重要性能之一，也逐渐受到人们的关注。如何优化汽车的振动、提高汽车的乘坐舒适性已成为每个设计部门的重要研究课题。虚拟样机技术的发展为研究汽车平顺性提供了非常有效的途径，缩短了新车的研发周期，减少研发成本。目前采用的将整车部件全部考虑为刚体的做法已不能满足仿真精度的要求，因此采用刚柔耦合的方法研究汽车平顺性是十分有必要的［1］。本文以某国产轿车为原型，利用多刚体理论［2］、有限元理论及模态综合法［3］，将前悬架稳定杆、下摆臂、后悬架扭转梁、车身考虑为柔性体，建立刚柔耦合整车模型。参考相关国家标准进行了该车平顺性仿真分析，并与多刚体模型的仿真分析及实车平顺性试验结果进行对比。结果表明:刚柔耦合整车模型具有较高的仿真精度。最后通过ADAMS软件的Insight模块对前后悬架的弹簧刚度和减振器阻尼进行了优化匹配。仿真结果表明:此次优化提高了该车的行驶平顺性。

1 整车刚柔藕合模型的建立

在汽车行驶过程中，前悬架的下摆臂、横向稳定杆、后悬架扭转梁、车身承受较大的力和力矩，这会造成它们的弹性变形，并引起车辆运动学参数的变化［4］。为提高仿真精度，本文将前悬架的下摆臂、横向稳定杆、后悬架扭转梁、车身考虑为柔性体，建立了前悬架、后悬架、横向稳定杆和车身为刚柔耦合结构的子系统，将动力总成、轮胎等其他子系统考虑为刚性体［5］。

为评价驾驶员的乘坐舒适性，本文建立了驾驶员－座椅系统模型，如图1所示。该模型把人体简化成质量为65 kg的刚体，通过简化为移动副的座椅与车身连接在一起，其中座椅的减振特性采用弹簧和阻尼器模拟，并通过设置弹簧和阻尼器的刚度值和阻尼大小代表座椅的弹性作用和阻尼作用。同时，在人体模型上建立了一个加速度测量仪，用以测量座椅面处人体受到的3个方向的加速度。刚柔耦合整车模型如图2所示。

在运用有限元软件Hyperworks对上述部件进行网格划分和有限元处理时［6］，考虑到仿真精度和计算时间的要求，设定网格大小为10 mm，然后运用模态综合法生成可以在ADMAS中分析的模态中性文件(MNF)，将其导入ADMAS中施加载荷和约束，建立刚柔耦合整车模型。在本文进行系统动力学仿真时选取前10阶模态。模态分析结果如表1所示。

图1 驾驶员－座椅系统模型

图2 刚柔耦合的整车模型

表1 刚柔耦合模型部件的模态

2 整车平顺性仿真分析

2.1 B级随机路面的建立

本文平顺性仿真采用ADAMS/Car Ride，它是专用的汽车平顺性仿真模块，可以快速准确地得出仿真结果。借助该模块的路面生成器，可以建立基于Sayers经验数字公式的B级路面。它还提供了左右轮辙路面轮廓参数，同时综合了很多不同类型的道路测量参数［7］。路面轮廓的功率谱密度Gd(n)和空间频率n有如式(1)所示的函数关系。

式中:Ge为空间功率谱密度幅值;Gs为速度功率谱密度幅值;Ga为加速度功率谱密度幅值。

本文在整车平顺性仿真时所选路面为沥青路面，取Ge=0，Gs=12，Ga=0.17。

2.2 随机路面输入下的平顺性仿真分析

参考GB/T4970—2009《汽车平顺性仿真实验方法》［8］的要求，在已经建立好的刚柔耦合整车模型和刚体整车模型的基础上，通过ADMAS/Ride平顺性仿真模块进行平顺性仿真。考虑到驾驶员经常在市区行驶的情况，本文将仿真车速分别设置为40，60，80 km/h，设置仿真时间为5 s，仿真频率设置为200 Hz。仿真完成后，利用后处理模块ADMAS/Post-Processor将驾驶员座椅处的加速度时间历程曲线进行FFT变换，得到驾驶员座椅处的加速度功率谱密度曲线。本文将给出60 km/h工况下的加速度曲线和加速度功率谱密度曲线，并对仿真结果进行讨论。

2.2.1 驾驶员位置垂向振动

由图3可知:在时域上多刚体模型座椅处垂向加速度变化范围为－0.745～0.930 m/s2，刚柔耦合模型座椅处垂向加速度变化范围为－0.704 0～0.782 1 m/s2，刚柔耦合模型座椅处垂向加速度比多刚体模型座椅处垂向加速度有一定减小，但变化趋势是一致的。在频域上刚柔耦合模型与多刚体模型的主要峰值频率完全对应。刚柔耦合模型在1.171 9 Hz的加速度功率谱密度的第1峰值为0.098 3 m2/s3，多刚体模型加速度功率谱密度的第1峰值为0.100 4 m2/s3，刚柔耦合模型的加速度功率谱密度的第1峰值小于多刚体模型。由此可以看出:柔性化后的部件并没有使车身的振动频率发生改变，只是降低了座椅垂向加速度值和垂向加速度功率谱密度的一部分幅值，这充分说明了柔性体的弹性变形能够吸收垂向振动能量。

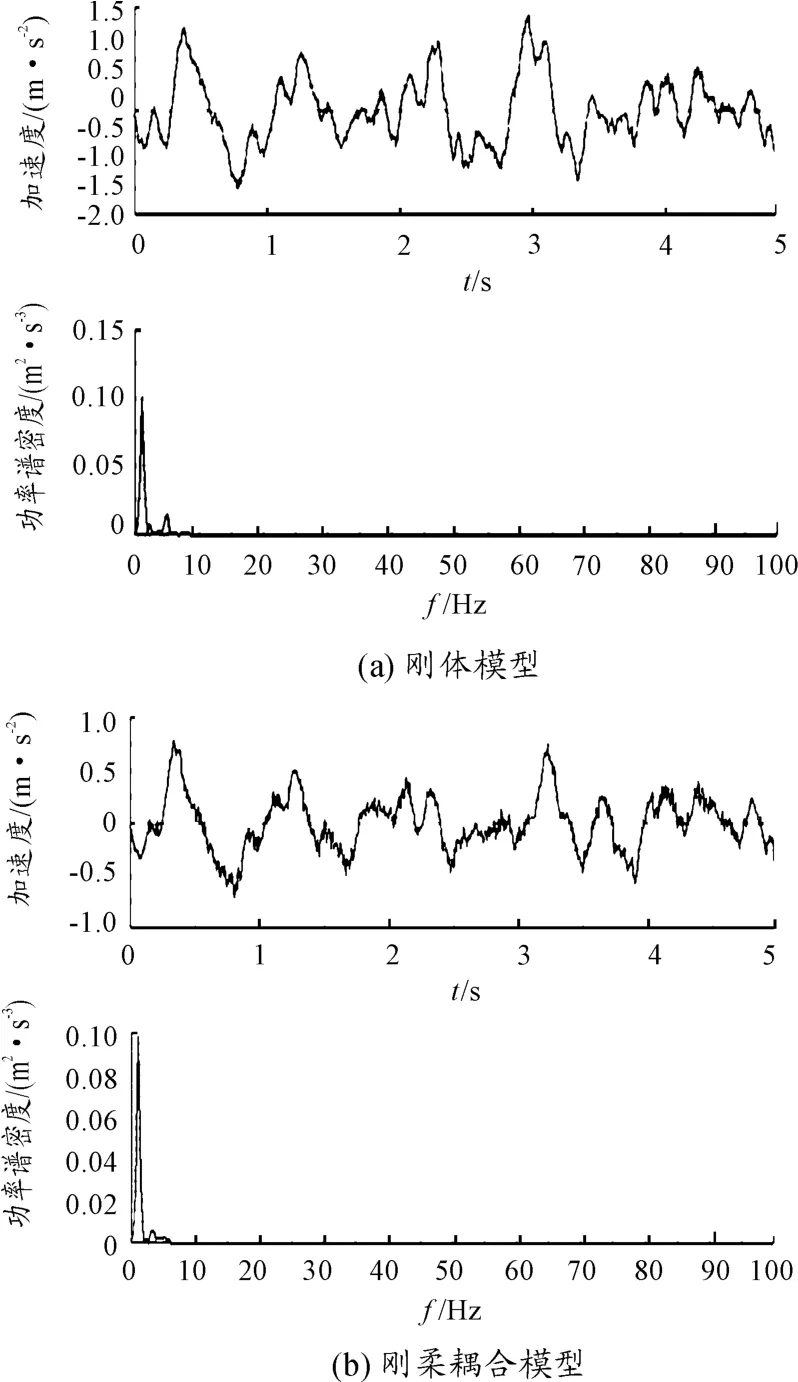
图3 不同模型驾驶员座椅处垂向加速度及加速度功率谱密度曲线

2.2.2 驾驶员位置横向振动

由图4可知:多刚体模型座椅处横向加速度变化范围为－0.506 2 ～0.511 8 m/s2，加速度均方根值为0.190 1 m/s2，而刚柔耦合模型中驾驶员座椅处横向加速度变化范围为－0.482 0～0.411 9 m/s2，其加速度均方根值为0.167 6 m/s2。通过对比可知:刚柔耦合模型的加速度曲线峰值、功率谱密度曲线峰值和均方根值比刚体模型小。这主要是因为刚柔耦合模型中的横向稳定杆被考虑成了柔性体，与横向稳定杆刚体模型做比较，柔性化的横向稳定杆可以发生变形，其能够吸收更多的车辆侧倾能量，使得刚柔耦合的整车模型比刚体模型的横向加速度要小。

图4 不同模型驾驶员座椅处横向加速度曲线及加速度功率谱密度曲线

2.2.3 驾驶员位置纵向振动

由图5可知:多刚体模型座椅处纵向加速度变化范围为－1.531 1 ～1.422 0 m/s2，加速度均方根值为0.438 7 m/s2，而刚柔耦合模型中座椅纵向加速度的变化范围为－1.153 3 ～1.141 4 m/s2，其加速度均方根值是0.364 7 m/s2。通过对比可知:刚柔耦合模型的加速度曲线峰值、功率谱密度曲线峰值和均方根值比刚体模型小。出现这种现象的主要原因是:刚柔耦合模型中前悬架下摆臂以及后悬架扭转梁被考虑成了柔性体，其自身存在弹性变形，一部分纵向的能量被其弹性变形吸收，所以使驾驶员位置的纵向加速度减小。

图5 不同模型驾驶员座椅处纵向加速度曲线及加速度功率谱密度曲线

3 平顺性实车道路试验

为对所建模型的准确性进行验证，选取某实车在某沥青道路上进行了平顺性随机输入试验，并比较了仿真与试验结果。在进行平顺性实车道路试验时，主要参考了GB/T 4970—2009，分别在驾驶员座椅及同侧后排座椅处放置三向加速度传感器，并在相对应的地板处放置三向加速度传感器。在实车平顺性试验中测点位置和仿真分析的测点位置大体是一致的。本文重点关注驾驶员座椅处的振动情况。

3.1 试验数据处理及结果

运用LMSTest.Lab14A对试验数据进行处理。截断频率选为100 Hz，有效分辨带宽为0.19 Hz。

在此主要给出驾驶员座椅处垂向振动加速度曲线与加速度功率谱密度曲线。该试验车辆经常用到的车速是60 km/h。由实车试验测量并处理数据后得到的驾驶员座椅处垂向加速度曲线与加速度功率谱密度曲线如图6、7所示。

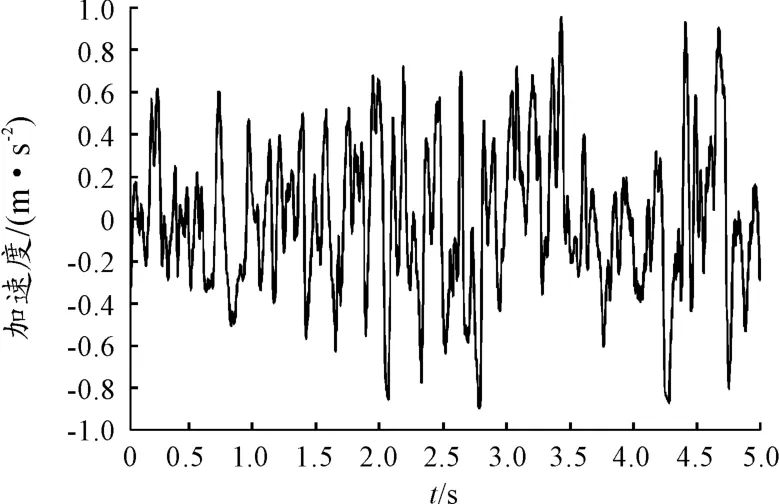
图6 驾驶员座椅处垂向振动加速度曲线(试验值)

图7 驾驶员座椅处垂向振动加速度功率谱密度(试验值)

3.2 结果对比及分析

将测量的驾驶员座椅处的振动加速度曲线输出到excel中计算出加权加速度均方根值，并经过数据处理后得到如表2和图8所示的平顺性仿真值与实车试验值的对比情况。

通过表2和图8可知:仿真结果和试验结果虽然有些差距，但变化趋势基本一致。从仿真结果和试验结果的对比来看，刚柔耦合模型的仿真结果和实车试验结果更为接近，仿真精度比刚体模型有所提高。因此本文采用刚柔耦合的方法来研究车辆动力学是切实可行的。

4 平顺性优化设计

考虑到人们对平顺性的高要求和提高车型的市场竞争力，本文将进一步改善该车的平顺性。就汽车系统而言，对汽车平顺性有影响的主要部件有汽车悬架、座椅、轮胎等［9］。本文利用ADAMS软件的Insight模块对前后悬架的弹簧刚度和减振器阻尼进行了优化匹配。

表2 平顺性仿真与试验值对比

图8 平顺性仿真与试验值对比

4.1 目标函数的确定

平顺性的主要评价指标是加权加速度均方根值。为全面改善平顺性，本文选取驾驶员座椅处x，y，z方向的总加权加速度均方根值av为优化的目标，其最小值为目标函数:

4.2 设计变量的筛选

在对实车进行平顺性优化时，需要考虑到工艺、制造成本及可行性等实际因素。因此，本文以前后悬架的弹簧刚度和阻尼为设计变量进行平顺性优化。设计变量为

其中:kf，kr为前后悬架弹簧刚度;cf，cr为前后悬架减震器阻尼。

4.3 约束函数的确定

4.3.1 刚度约束

轿车悬架的静挠度f的设计范围一般为100～300 mm，由此可得前后悬架的刚度约束范围:

式中:Mf，Mr分别代表前后悬架的簧载质量。

为满足平顺性的要求，对前后悬架刚度进行匹配。可建立约束条件:

4.3.2 阻尼约束

在悬架减振器设计中，评价振动衰减的快慢程度时一般采用阻尼比ξ，其计算公式为

参考相关资料［10］取ξ=0.23～0.28，因此阻尼系数的约束为:

4.3.3 试验条件约束

各变量系数的约束范围:

式中:n(Kf)，n(Kr)，n(Cf)，n(Cr)分别为前后悬架的刚度和阻尼系数。

4.4 优化计算

在ADAMS软件的 Insight模块中，采用 DOptimal优化类型对刚柔耦合整车模型进行优化。模型以60 km/h的速度在B级激励路面上匀速行驶，通过多次对弹簧刚度和减振器阻尼参数进行调整，求出优化目标总加权均方根值av的最小值。优化前后弹簧刚度、减震器阻尼系数、评价指标如表3所示，优化前后垂向加速度功率谱密度曲线如图9、10所示。

表3 优化前后悬架刚度、阻尼及评价指标值

图9 优化前垂向加速度功率谱密度曲线

图10 优化后垂向加速度功率谱密度曲线

由图12可知:优化前驾驶员座椅处垂向加速度功率谱密度最大峰值处频率为1.171 9 Hz，对应峰值是0.098 3 m2/s3。由图13可知:优化后加速度功率谱密度峰值明显降低，最大峰值处频率为1.171 9 Hz，对应峰值是0.039 8 m2/s3。经数据计算，优化前的总加权加速度均方根值 av=0.281 m/s2，优化后 av=0.26 m/s2。

车辆在40 km/h速度行驶下，优化后其加速度均方根值 av=0.201 m/s2，优化前 av=0.216 m/s2。车辆在80 km/h速度行驶下，优化后加速度均方根值 av=0.316 m/s2，优化前 av=0.341 m/s2。说明优化后车辆的平顺性得到了较好的改善，证明本次悬架参数优化是成功的。

5 结论

本文以某轿车为原型，利用有限元软件Hyperworks与机械系统仿真软件ADMAS建立了刚柔耦合整车模型。通过在B级路面上进行多刚体模型与刚柔耦合模型平顺性仿真与实车试验，并对该车行驶平顺性进行优化，得出以下结论:

1)对于驾驶员座椅处的垂向振动，在频域上刚柔耦合模型与刚体模型的主要峰值频率完全对应，由此看出柔性化后的部件并没有使车身的振动频率发生改变。

2)相比刚体模型，刚柔耦合模型座椅处的横向、纵向、垂向的加速度都有所减小。这是由于刚柔耦合模型中自身存在弹性变形，一部分能量被其弹性变形吸收。

3)刚柔耦合模型的仿真结果和实车试验结果更为接近，仿真精度比刚体模型有所提高，因此本文采用刚柔耦合的方法来研究车辆动力学是切实可行的。

4)以驾驶员座椅处加权加速度均方根值作为优化目标、以该车悬架参数作为优化变量对该车进行了平顺性优化。与优化前的仿真结果进行对比，表明该车的平顺性得到了改善。

［1］张越今.多体系统动力学在轿车动力学仿真及优化研究中的应用［D］.北京:清华大学，1997.

［2］SHABANA A A.An absolutenodal coordinates formulation for the large rotation and defor-mation analysis of flexible bodies［Z］.Chicago:University of Illinois at Chicago，1996.

［3］陈宝，李灿，刘圣坤.含橡胶衬套的后悬架柔性扭力梁结构优化［J］.重庆理工大学学报(自然科学版)，2012，26(2):6－10.

［4］欧健，张青林，杨鄂川.考虑悬架柔性的刚柔耦合汽车平顺性研究［J］.机械设计与制造，2015(2):132－138.

［5］张勇，陈宝，石智卫.整车刚柔耦合动力学模型及平顺性优化［J］.西南师范大学学报:自然科学版，2012，37(5):68－72.

［6］余志生.汽车理论［M］.北京:机械工业出版社，2007.

［7］石晶，孙艳，陈双.微型电动汽车平顺性仿真分析与试验研究［J］.科学技术与工程，2014，14(34):293－297.

［8］汽车平顺性试验方法:GB/T4970－2009［S］.

［9］过吉生.基于虚拟样机技术的轿车平顺性仿真分析及优化设计［D］.重庆:重庆理工大学，2010.

［10］裴未迟，张文明，乔长胜.基于ADAMS微型观光旅游电动汽车平顺性优化［J］.科学技术与工程，2014，14(6):251－255.