部分入水悬臂梁的自由弯曲振动固有特性研究

刘少文，林泽峰，杨翊仁

(西南交通大学力学与工程学院，成都 610031)

悬臂梁的振动是一类重要的力学模型。由于实际需要，许多真实物体是放置在水中的，例如桥墩，它们可以被认为是悬臂梁置于水中，对其振动分析时，水的作用是不能忽视的。悬臂梁在水中的固有特性研究是一个具有理论和实际意义的课题，它属于流固耦合动力学分析领域。在现有研究中，许多情况下考虑水深与梁高相等，然后用无水情况下的梁自由振动的振型函数作为基函数，将有水振型函数按无水振型函数作级数展开［1－2］，或者是考虑部分有水情况时直接将两段方程分别列出来，求出两段的带系数的精确解，然后根据梁的边界条件和两段对接条件列出以待定系数为未知量的线性方程组进行求解［3］。本文对不同水深情况下梁振动的固有频率的变化情况进行了探讨，并使用Galerkin离散法和以ANSYS软件为平台的有限元法两种方法进行计算和结果对比，给出了圆截面梁的前两阶固有频率随水深的变化规律［4－15］。

1 振动方程的建立

悬臂梁坐标示意图如图1所示。考虑悬臂梁竖直放置，其长度为H，入水部分为0～h，悬臂梁横截面为半径为a的圆，则由振动力学理论可知梁在空气中的横向自由振动的振动方程为:

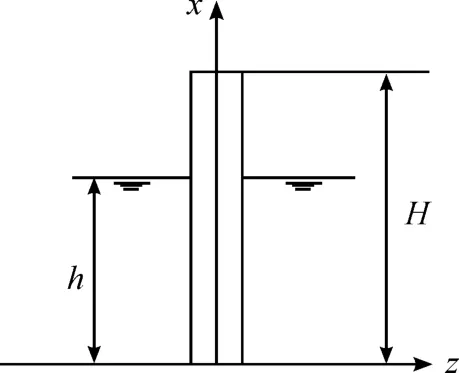
图1 悬臂梁坐标示意图

梁作简谐振动，则令

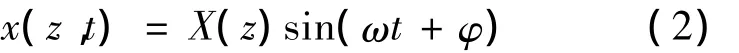
代入式(1)可得

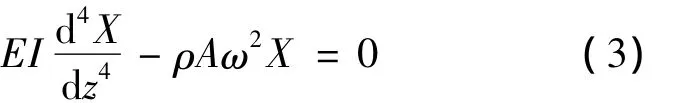
其中:EI为梁的弯曲刚度;ρ为梁的密度;A为横截面积。

对于入水悬臂梁部分，本文进行如下假设:水为不可压缩、无黏性的理想流体，并且忽略水表面自由波的影响。则流体运动的速度势ψ满足Laplace方程，其在柱坐标中的形式为

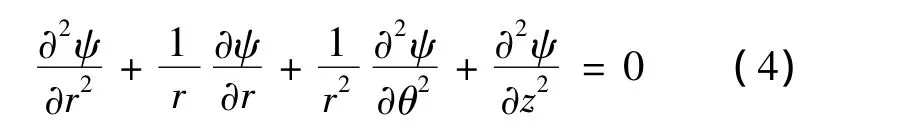
使用分离变量法，令

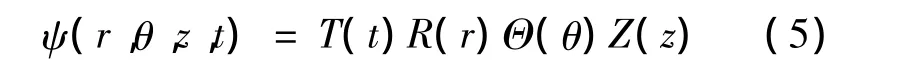
代入方程(4)，并根据相应边界条件可得［3］:

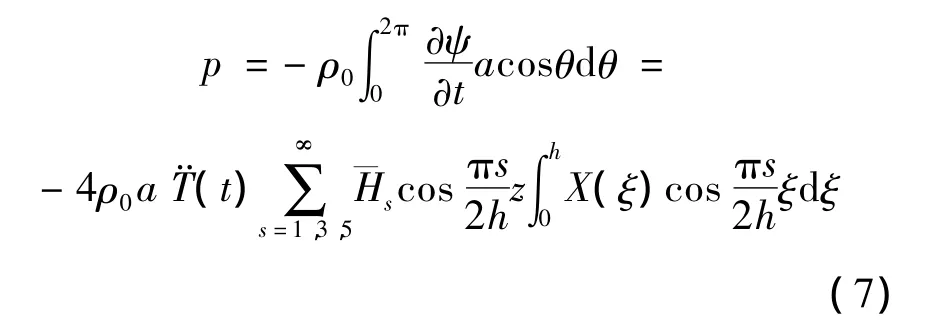
其中:h为水的深度;ρ0为水的密度。因此入水部分梁的弯曲自由振动方程为

自由振动时，梁振型随时间变化为谐振规律，消去时间项则可将方程(8)变为如下形式:

综合方程(1)和方程(9)，可以得到该悬臂梁的横向振动方程为:

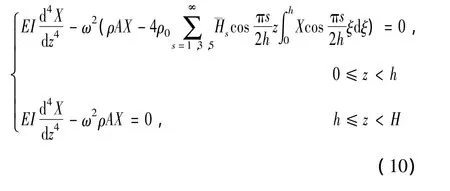
2 振动方程的求解

采用Galerkin法离散方程(10)。根据Galerkin法的原理，若系统振动方程为L(X)－λM(X)=0，L，则 M为2p次微分算子。选取比较函数X1，X2，…，Xn，令，则应该满足

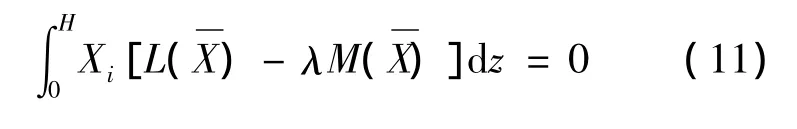
本文选取:

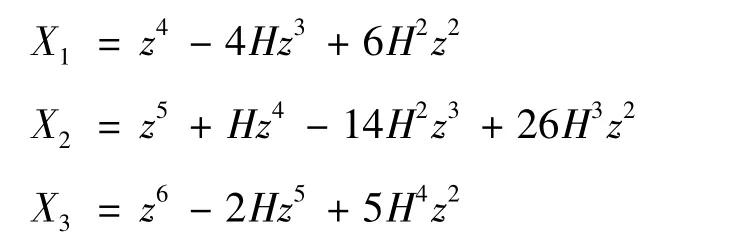
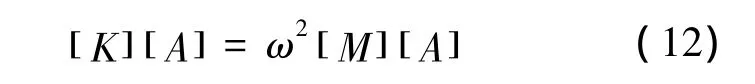
其中:

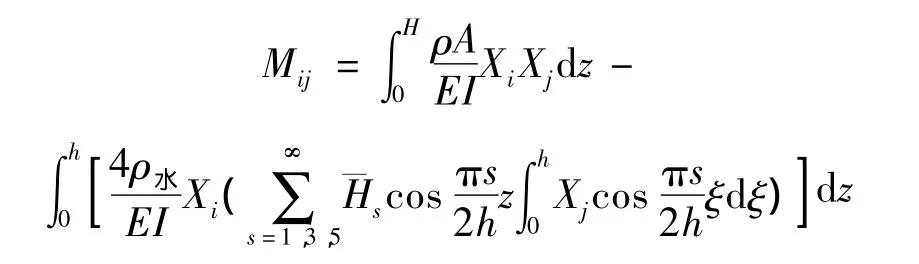
式(12)存在非零解的条件为

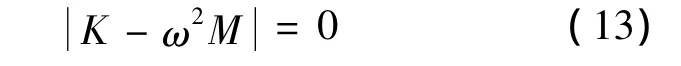
解此广义特征值问题，变化水深参数h就可以得到部分入水悬臂梁的前两阶固有频率随水深的变化规律。

3 算例

取a=0.02 m，H=1 m，ρ=2 400 kg/m3，ρ0=1 000 kg/m3，E=2.44 GPa，水深变化可以分别取h=0，0.2，0.4，0.6，0.8，1 m，计算得到部分入水悬臂梁的前两阶固有频率见表1。

为了对比计算结果的精度，本文还使用了有限元方法分析该系统，分析过程在ANSYS软件平台上进行。

本算例中，悬臂梁使用solid45单元模拟，水使用fluid30单元模拟，水和梁的几何模型均为圆柱体。为了使分析结果更加精确，水模型的半径设置为梁半径的10倍。将梁单元和水单元接触的地方使用FSI方法进行耦合，施加相应的约束条件后变化水深参数，分别进行模态分析就能得到梁的前两阶固有频率随水深的变化规律，如表2所示。

表1 采用Galerkin法计算的不同水深下的前两阶固有频率

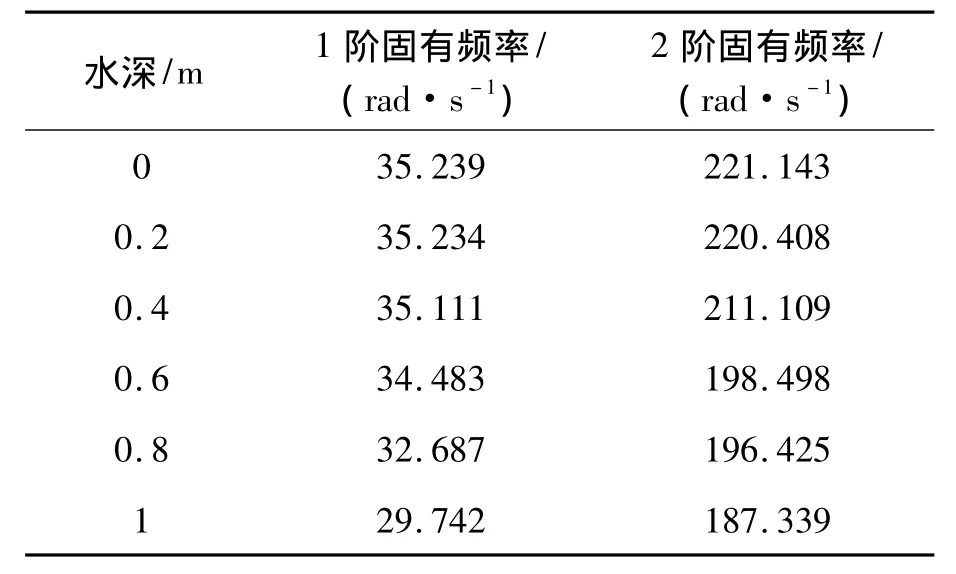
表2 采用ANSYS计算的不同水深下的前两阶固有频率

将表1和表2中的相应数据进行拟合，分别得到两种方法计算的1阶固有频率和2阶固有频率随水深的变化情况曲线，见图2和3。

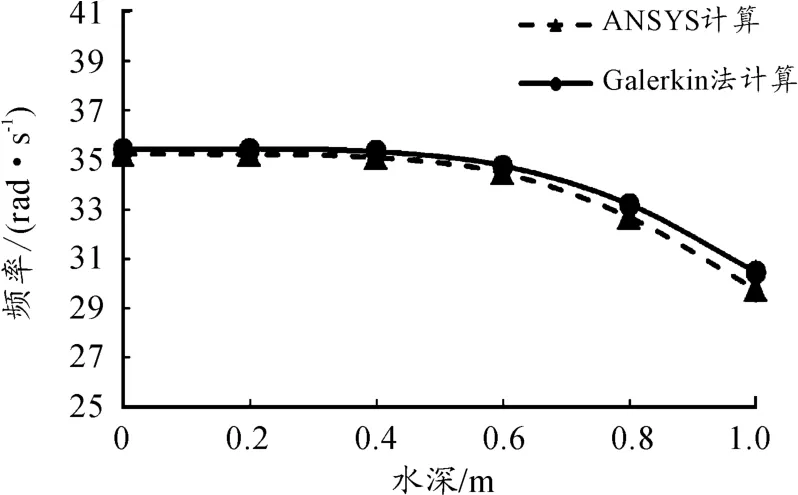
图2 不同水深1阶固有频率对比曲线

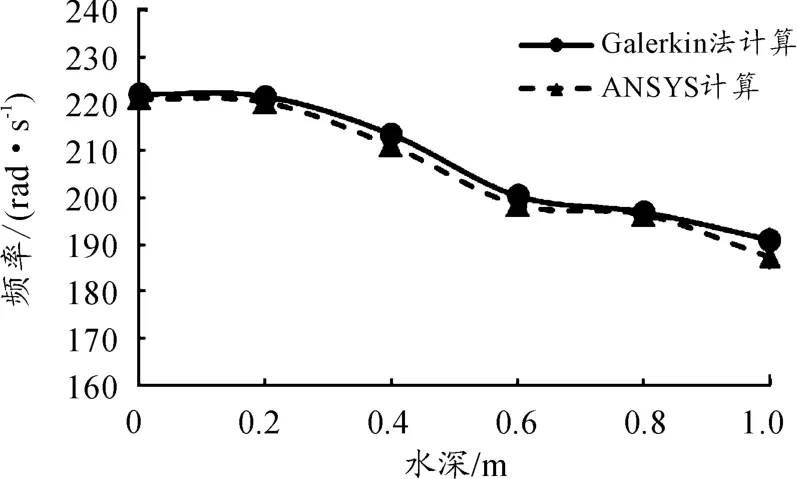
图3 不同水深2阶固有频率对比曲线

从图2和3中可以看出:悬臂梁的前两阶固有频率随水深的增加而下降。为了更加清晰地得到下降的具体情况，将不同水深下的弯曲梁固有频率同无水情况下固有频率作比值，令比值为c，可以得到比值c随水深的变化情况，如图4和5所示。

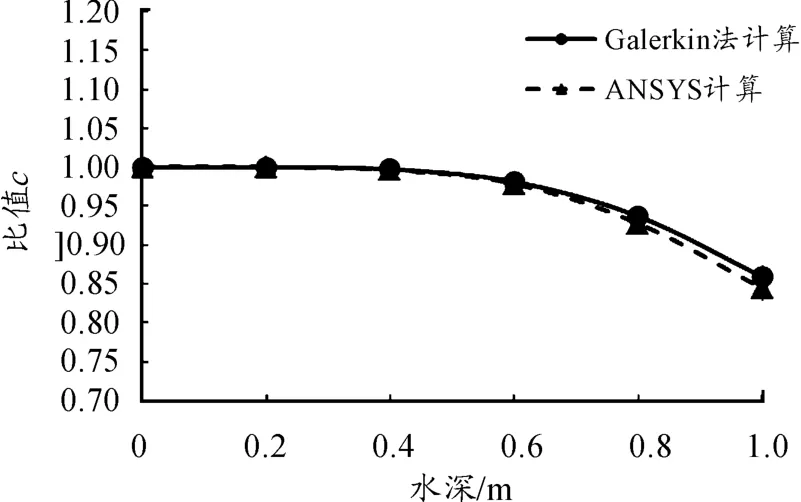
图4 不同水深的一阶固有频率比值对比曲线

图5 不同水深的二阶固有频率比值对比曲线

4 结论

通过计算结果可知:随着水深的增加，圆截面悬臂梁弯曲振动的前两阶固有频率逐渐减小。满水时，采用Galerkin法计算的1阶固有频率减为无水频率的85.91%，采用ANSYS软件计算的则为无水频率的84.40%。同样，2阶固有频率减为无水频率的 85.97%(Galerkin法计算结果)和84.71%(ANSYS软件计算结果)。计算结果表明:水对于悬臂梁振动的影响相当于分布附加质量的作用，附加质量随着水深增加而增大，附加质量的影响降低了梁的固有振动频率。

［1］居初荣，曾心传.弹性固体与液体的耦联振动分析［M］.北京:地震出版社，1983.

［2］杨万理.深水桥梁动水压力分析方法研究［D］.成都:西南交通大学，2013.

［3］张悉德.部分埋入水中悬臂圆柱体的弯曲自由振动［J］.应用数学和力学，1982(4):537－546.

［4］周叮.两侧受液时悬臂梁的自由振动分析［J］.工程力学，1991(3):107－115.

［5］张敏.桥墩与河水流固耦合振动分析［D］.大连:大连交通大学，2006.

［6］杨吉新，党慧慧，雷凡.考虑水作用的桥墩自振特性计算方法对比分析［J］.世界地震工程，2010，26(3):91－95.

［7］陈贵清，杨翊仁.板状梁结构的流致振动研究［J］.学术动态，2003(2):31－33.

［8］刘振宇.深水桥梁的地震响应分析［D］.成都:西南交通大学，2007.

［9］苏海东.分析流固耦振的新方法及其应用研究［D］.武汉:华中科技大学，2007.

［10］杨笑冬.基于ANSYS的悬臂梁模态分析［J］.机电一体化，2008(6):58－60.

［11］张阿漫，戴绍仕.流固耦合动力学［M］.北京:国防工业出版社，2011.

［12］Sharan S K.Hydrodynamic loadings due to the motion of large offshore structures［J］.Computers ＆ Structures，1989，32(6):132－137.

［13］戴大农，王勖成，杜庆华.流固耦合系统动力响应的模态分析理论［J］.固体力学学报，1990，11(4).

［14］刘雪莱.基于流固耦合的冷却风扇叶片模态及疲劳分析［J］.重庆理工大学学报:自然科学版，2014(9):25－30.

［15］田彦伟，崔晓娜.三维拉普拉斯方程的求解［J］.安阳师范学院学报，2007，10(5):3－5.