冷板传热特性的计算流体力学仿真方法

吴 刚，朱雅鹏，周守锋，张瑜珊

(西安机电信息技术研究所，西安 710065)

大功率电子模块广泛应用在交通控制、功率变换、工业电机、不间断电源、风电与太阳能设备等领域。伴随着大功率电子模块的热流密度日益提高，对其冷却系统的散热能力提出了越来越高的技术要求。通常当大功率电子模块的热流密度大于0.6 W/cm2时，液体冷却将成为冷却方式的最佳选择［1］。液体冷却中最常见的是冷板，冷却介质在冷板内置的通道内流过，带走安装在冷板上的电子元器件所耗散的热量。

大功率电子模块用冷板的传热特性(主要包括温度场分布情况和热效率)的研究成果多限于单一工况条件下的传热特性分析，即电子模块在某一定值功率输出条件下所对应的传热特性。文献［2］分析了直线型流道、S型流道和有内置分流片的S型流道3种冷板在单一工况条件下的流场和温度场分布情况，得出有内置分流片的S型流道热效率最高。文献［3］研究了中间入口的S型流道、双S型流道和中间入口的双S型流道3种改进的流道结构在单一工况条件下的温度场分布和流动情况，实验结果表明:中间入口的S型流道具有最佳的热效率和流动综合性能。文献［4］对不同翅片结构的冷板在单一工况下的温度分布进行分析，通过实验得出X型翅片结构的冷板比直线型翅片冷板温度场分布更加合理。以上文献多限于研究单一工况条件下冷板流道结构的变化和冷板翅片结构变化对应的传热特性。

在实际的工程应用中，大功率电子模块工作环境通常比较复杂，需要在不同工况条件下工作，根据实际情况需要频繁切换功率输出状态，不同工况对应着电子模块不同的功率输出，即不同的热量耗散，其工况变化会使冷板的传热特性也发生相应的变化。此时冷板在倍增的电子模块发热功率下温度分布的变化规律和相应的热效率变化情况不明。由于对电子模块的散热不良区域位置不了解，因此无法对热量集中区域采取必要冷却措施，同时对相应的热效率情况也不清楚，不知道冷板散热情况是否达到饱和状态，是否有一定的散热潜力可供挖掘。对冷板在不同工况条件下的传热特性的正确认识是确保电子模块正常运行的重要前提。大功率电子模块用冷板在不同工况条件下的温升是否是线性关系，热效率如何变化等传热特性研究成果尚未见相关报道。本文提出冷板在不同工况下传热特性的计算流体力学仿真方法。

1 计算流体力学仿真的一般方法

1.1 电子模块集成冷板的结构

一典型结构的大功率电子模块由6个IGBT(绝缘栅双极型晶体管)及冷板组成。每个IGBT尺寸为100 mm×60 mm，每2个IGBT为1组，3组排1行，组与组芯片之间的间距为30 mm，每组内部芯片的间距为3 mm。冷板尺寸为720 mm×250 mm×30 mm，由6063铝基板与T2紫铜管组成。IGBT位于T2紫铜管正上方，冷却液从管内流过。电子模块集成冷板的结构如图1所示。表1列出该冷板的相关参数。

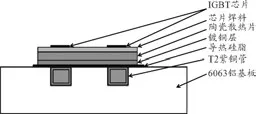
图1 电子模块集成冷板的结构

表1 冷板相关参数

1.2 计算流体力学仿真的一般方法

使用计算流体力学方法进行仿真，可借助商业软件来完成需要的任务，也可直接编写计算程序，两种方法的基本工作过程是一致的［5－9］。仿真主要分5步:建模;定义边界条件;网格划分;计算;后处理。其中50%以上的工作量花在建模和网格划分上。可以使用商业软件自身的前处理器生成几何模型，也可以借用其他商业CAD/CAE软件生成的模型。边界条件是在求解区域的边界上所求解的变量或其导数随时间和地点的变化规律。定义的边界条件包括工作环境条件、求解域、热元件物性参数、散热功率等。网格如何划分直接决定求解的精度和速度。在保持适当精度的前提下，应尽量减少网格数，寻求计算精度和网格数的最佳平衡点。计算的核心是数值求解方案，常用的求解方案包括有限差分、有限元、谱方法和有限体积法等。后处理则将计算过程得出的各个节点的解以适当的手段表示出来，一般通过线值图、矢量图、等值线图、流线图、云图等方式对计算结果进行表示。

2 冷板传热特性的计算流体力学仿真方法

2.1 建模

计算流体力学方法对冷板在不同工况下的传热过程进行数值模拟。首先建立传热过程模型。建模前需要对电子模块元器件组成和传热过程分别进行必要的简化。大功率电子模块上的元器件都向外散发热量，但散热功率差别巨大，甚至是几个数量级的。将散热功率微小的元器件忽略不计，计算时仅考虑散热量大的元器件，简化了电子模块元器件组成。冷板真实的传热过程包括传导、对流、辐射3种方式，但由于辐射传热的功率低，此方式可忽略不计。冷板传热过程简化为液体流动换热、固－液对流换热及固体导热的耦合传热问题。建模前需要对流体的属性参数作出以下假设:①流体的物性参数为常数;②流体定常流动;③流体不可压缩;④流体在壁面无滑移，即壁面处的流速为0。完成上述简化和假设后，即可向软件输入几何模型，定义所求问题模型的相关数据，完成建模工作。

2.2 定义边界条件

数值模拟过程中边界条件的设置最难掌握，但却对计算结果有重要的影响。根据对冷板传热过程作出的假设设置以下边界条件:①IGBT处的等热流密度边界;② 冷板入口水流速;③ 出口的局部单向化边界条件。由于本文所涉及的传热过程是稳态问题，所以不需要初始条件。

2.3 网格划分和计算

网格划分是一个“漫长而枯燥”的工作过程，因此出现了许多商品化的专业网格生成软件，可以利用这些工具进行网格划分。此方法没有特别之处，但需要进行大量的尝试才能够取得最佳的划分结果。控制方程的求解采用压力耦合方程组的半隐式方法(SIMPLE算法)，此算法是目前工程上应用最为广泛的一种流场计算方法，具有适用范围宽广、收敛速度快捷的特点。

2.4 后处理

首先利用基于热力学获得的冷却剂流量作为初始值，将其代入数值模拟过程，可以得到冷板的温度场分布云图。通过云图发现其满足冷板的散热要求，但是其冗余量很大，会提高冷却系统的水泵性能要求，增加制造成本，降低系统的可靠性。反之，如果偏小，又会造成系统温度过高、温升失控等问题，将威胁电子模块的生命。将冷却剂流量初始值逐步降低，通过多次的仿真迭代分析使其接近真实的最优值。该最优结果既能满足冷板在不同工况下的散热需求，同时热效率相对最高，从而对冷却系统的水泵硬件条件要求降低，达到效能比最高的要求。最后，以流量最优值为已知参数代入单一工况条件下的仿真过程，能够得到一个温度场的分布云图，进一步可得到热效率。以流量最优值为已知参数代入不同工况条件下的仿真过程，能够得到多个温度场的分布云图，进一步可得对应的热效率，从而仿真得到冷板在不同工况下的传热特性。

3 仿真与实验验证

3.1 仿真实例

上述结构的电子模块需要在6种不同的功率输出模式下正常工作，不同工况下的热耗散功率参数见表2，其中最大热耗散功率约是最小值的4.3倍。利用计算流体力学方法仿真得到的冷板温度分布云图从理论上可以获得温度场上任意一点的温度值，得到冷板的温度场分布情况，进一步可得到冷板的热效率，从而全面掌握冷板传热性能。

表2 散热元器件参数

上述结构的电子模块在6种不同工况下的温度仿真结果见图2。当冷却液进口温度为19.7℃，流速为4 LPM时，选择电子模块上的5个典型的工位点(包括冷却剂进、出口处，冷板上最高温度处，最低温度处，随机一处)作为测试点，它们在6种不同工况下的温度场分布情况如下:冷板在热耗散功率成倍增加的工况下，温度场分布规律表现出很高一致性，电子模块上任意一点的温度值都伴随着耗散功率的增加而提高，但并非是线性关系;当热元件耗散功率是最低功率的2倍时，5个测试点温差很小，可见此时冷板将IGBT耗散的热量绝大部分吸收，冷却液通过对流的形式将热量带走;随着耗散功率进一步增大，电子模块的温度升高比较明显。当元器件耗散功率增加到最小值的3.2倍时，温度大约升高20%;当元件耗散功率增加到最小值的4.3倍时，温度大约升高30%。通过仿真温度场，可以得到在6种工作载荷下的冷板热效率。当元器件处于中低耗散功率时，冷板热效率接近100%;在最高耗散功率时，冷板热效率接近90%。

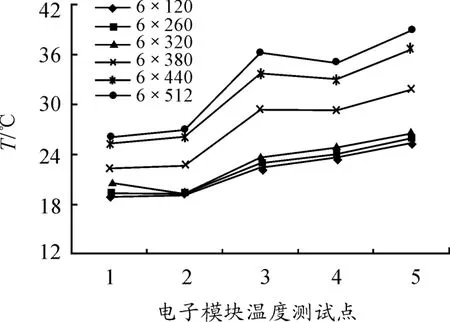
图2 不同工况下电子模板测试点温度仿真值

3.2 实验平台和实验结果

这里对冷板的传热性能进行实验验证，以对仿真结果进行检验。实验流程如图3所示。循环水路的动力由水泵提供，流速通过安装在主回路和储水箱支管上的3个阀门来调节。芯片产生的热量由空气－水换热器带到周围环境中。冷板的进出口水温通过2个热电偶测量，流速通过流量计进行测量。芯片及冷板上表面的温度通过17个热电偶测得。通过热电偶测得电子模块的某一位置的实时温度得到温度场的分布规律，进一步可得冷板的热效率。

图3 实验流程

实验结果显示19处热电偶测得的温度值表现出一致的特性。图4是在冷却液入口温度为19.7℃，流速为4 LPM的情况下，电子模块在6种不同工况下的最高温度情况。由图4可知测得的温度峰值均大于仿真值，其中最小的误差为8%，最大的误差为15%，但都在合理的范围内(传热过程的热力学仿真存在一定的计算误差，一般在30%左右，如果将误差控制在20%左右已经算是精确的结果)。可以看到电子模块在热耗散功率成倍增加的工况下，温度场分布规律表现出很强的一致性，为一种非线性的特征，当最大的热负荷是最小值4.3倍时电子模板的最高温度上升了22%。

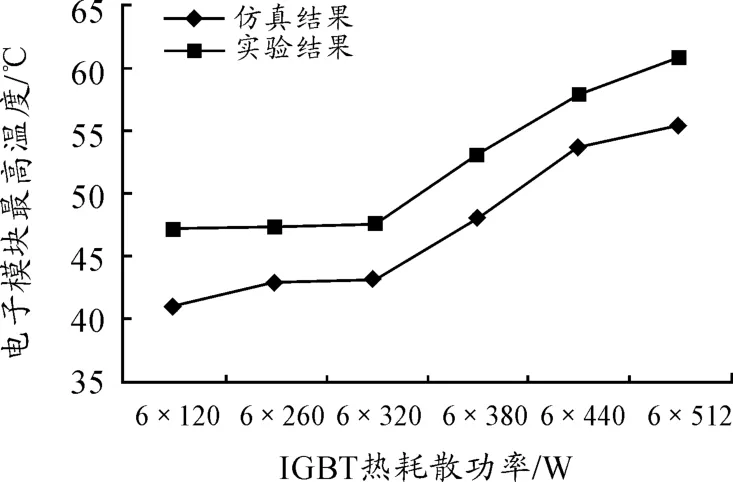
图4 不同工况下电子模块的最高温度

图5为在冷却液入口温度为19.7℃，流速为4 LPM的情况下，冷板在6种不同工况下的热效率。由图5可知实验获得的热效率值均小于仿真值，即冷板真实的热效率比仿真结果低。可以看到在低耗散功率下，冷板的散热效率达到90%左右，可将电子模块绝大部分热量带走。当耗散功率最大时，冷板热效率降至74%。这体现了传热模型复杂性:在一个传热的过程中，热传导、对流传热、辐射传热都有参与，但各自在传热的过程中所占比例不同，而且伴随着传热工况的变化而改变。伴随着热元件耗散功率的增大，冷板的热效率逐渐降低。上述实验结果与仿真所得出的温度特性表现出的趋势是一致的。

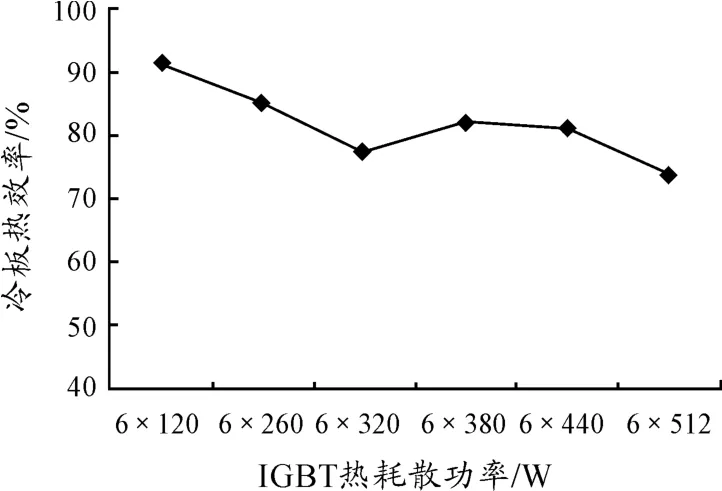
图5 不同工况下冷板的热效率

3.3 实验结果分析

冷板传热特性的仿真结果与实验结果表现出一致的趋势，可以看到基于计算流体力学方法的仿真模型对冷板的传热特性模拟得比较准确。两种方法都表现出伴随着电子模块散热功率的成倍增加，电子模块温升与冷板的传热量并不是简单的线性关系。仿真结果与实验结果存在一定的误差，表现在仿真获得的温度值比真实值低，热效率比真实值高。这主要是由于在仿真分析过程中设定了一些理想化的条件，以及计算流体力学分析方法自身存在一定的局限性，程序的编制在很大程度上依赖于个人的经验和技巧等，因此仿真结果必然与实验结果有一定的误差，但不足以影响对冷板传热特性的正确认知。通过实验测量方法可以得到冷板的传热特性，但是实验往往受模型尺寸、流场扰动、测试人员安全和测量精度的限制，对于某些特殊情况可能很难通过实验方法得到结果。此外，实验还会遇到经费、人力、物力的巨大耗费及周期长等许多困难。基于计算流体力学方法的数值模拟克服了实验测量方法的弱点，在计算机上实现特定的计算，就好像在计算机上做了一系列物理实验，最终可以直观地表现冷板的传热特性。哪些区域温度过高或散热情况不良等，通过仿真可以做到一目了然，心中有数。

4 结束语

本文提出冷板在不同工况下的传热特性的计算流体力学仿真方法。通过对电子模块元器件组成和传热过程进行简化，对流体的属性参数进行假设，简化传热模型，设置边界条件，选择SIMPLE算法作为控制方程的求解算法，仿真得到冷板在不同工况下传热特性。实验结果表明:基于计算流体力学方法的仿真模型对冷板在不同工况下的传热特性的模拟比较准确。

［1］邱成悌，赵悖殳，蒋全兴.电子设备结构设计原理［M］.南京:东南大学出版社，2005.

［2］余小玲，张荣婷，冯全科.大功率模块用新型冷板的传热性能研究［J］.航天器环境工程，2009，43(12):79－81.

［3］梁雪艳，孙志坚，黄秋月.LED模块用液冷基板的流道和换热性能研究［J］.中国照明电器，2012(1):6－10.

［4］孙娟，刘国清，裴一飞.真空条件下冷板传热分析［J］.电力电子技术，2010，27(1):67－70.

［5］王福军.计算流体力动力学分析——CFD软件原理与应用［M］.北京:清华大学出版社，2004.

［6］陈耀松，单肖文，陈沪东.计算流体力学的新方向及其在工业上的应用［J］.中国科学(E辑:技术科学)，2007(9):1107－1116.

［7］祝银海，厉彦忠.板翅式换热器翅片通道中流体流动与传热的计算流体力学模拟［J］.化工学报，2006(5):1102－1106.

［8］张仂，谷芳.基于计算流体力学热流固耦合仿真的换热器折流板结构优化［J］.石油化工，2012(6):682－687.

［9］张杨，吴哲，曹军.基于计算流体力学的木材干燥窑内三维流场的数值模拟［J］.东北林业大学学报，2013(12):135－140.