一类生物过程的稳态优化
高群王,徐恭贤,王佳星
(渤海大学数理学院,辽宁锦州 121013)
1,3-丙二醇具有广泛的应用领域,如在聚合材料的单体、化妆品、润滑剂、医药等方面。1,3-丙二醇的生物合成尤其在工业领域有潜在价值,这主要是因为1,3-丙二醇成本低且无污染[1-3]。欧共体国家、美国、加拿大等大多采用化学合成法生产。然而,与传统的化学合成法相比,微生物法具有转化率高、副产物少、环境污染小等优点[4],但很难提高1,3-丙二醇的浓度。因此,提高1,3-丙二醇的产量备受全球关注。
近年来,甘油生物歧化为1,3-丙二醇过程的非线性动力学系统被学者们广泛研究。文献[5]运用过量动力学模型研究甘油转化过程中的动态行为;文献[6]通过引入过量项对过量动力学模型进行了修改,修改后的模型研究了实验中的多稳态现象。在文献[6]中建立的五维模型基础上,文献[7-11]针对甘油转化1,3-丙二醇的连续发酵过程研究了参数辨识、平衡点的稳定性分析、振荡现象和时滞现象。文献[12-15]针对间歇发酵、连续发酵和批式流加发酵过程研究其参数辨识问题;文献[16]应用AISOPE算法研究了甘油生物歧化为1,3-丙二醇过程的优化控制;文献[17]采用加权和及NBI两种方法求解其建立的多目标优化模型;文献[18]证明了间歇发酵系统的稳定性;文献[19]建立了甘油生物歧化为1,3-丙二醇过程的还原途径酶催化八维非线性动力系统。但迄今为止未见有关于该生物过程稳态优化研究的报道。
本文针对孙亚琴建立的甘油生物歧化为1,3-丙二醇过程的还原途径酶催化八维非线性动力系统,提出了一个使主要产物1,3-丙二醇产率达到最大的稳态优化模型,并应用内点法对其进行求解,取得了较好的应用效果。
1 动力学模型
本文考虑如下甘油生物歧化为1,3-丙二醇过程的还原途径酶催化八维非线性动力系统[19-21]:

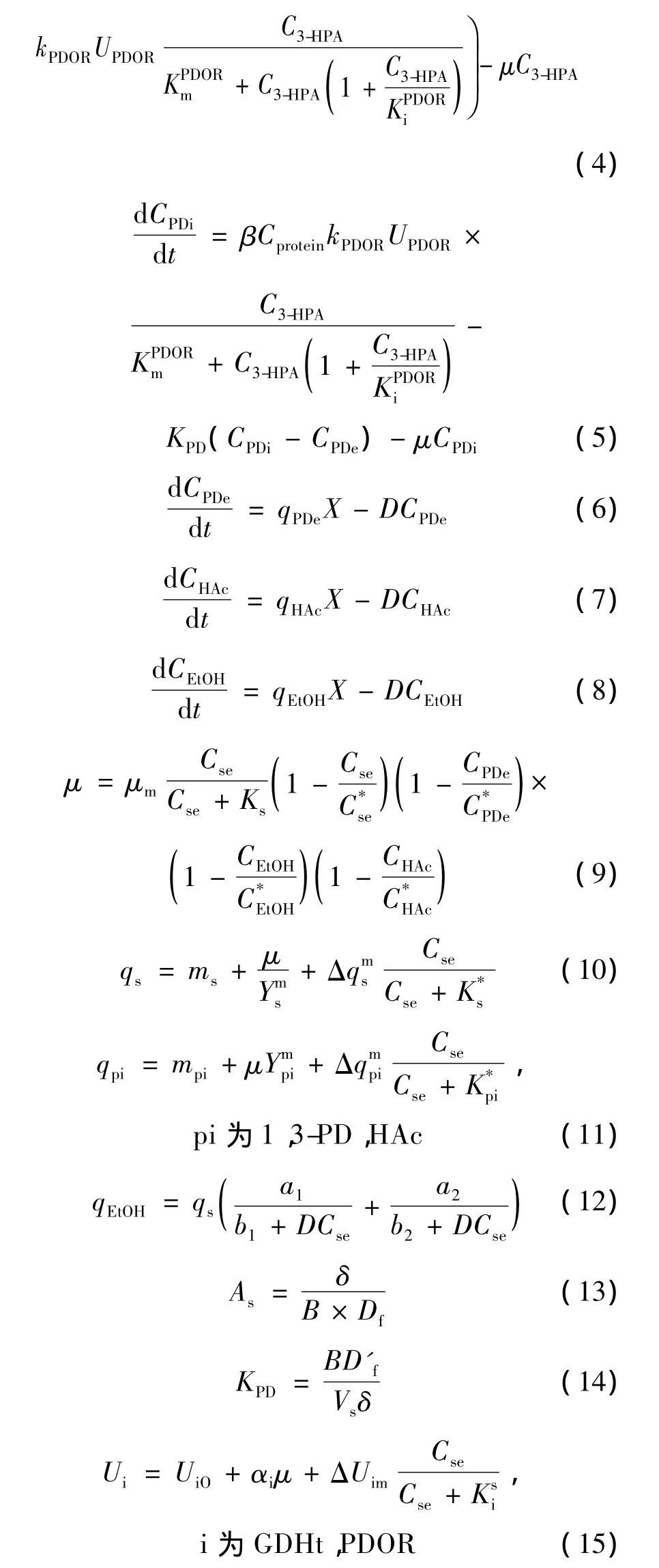
其中:X为生物量浓度(g/L);D为稀释速率(h-1);Cso,Cse,Csi分别为进料底物浓度、反应器中胞外和胞内甘油浓度(mmol/L);C3-HPA为胞内3-羟基丙醛浓度(mmol/L);CPDi,CPDe分别为胞内和胞外 1,3-丙二醇浓度(mmol/L);CHAc为胞外乙酸浓度(mmol/L);CEtOH为胞外乙醇浓度(mmol/L);μ,qs,qpi,qEtOH(pi为1,3-PD,HAc)分别为细胞比生长速率、底物比消耗速率、产物1,3-丙二醇和乙酸的比生成速率及乙醇的比生成速率(mmol/(g·h));t为发酵时间(h);其余参数意义见附录,取值如表1所示。
表1 式(1)~(15)中的参数取值

参数 取值 参数 取值Vs 0.151 L/g Ym 0.008 2 g/mmol Jmax 54.664 mmoL/(g·h) Ym1,3-PD s 67.69 mmol/g Km 1.340 mmol/L YmHAc 33.07 mmol/g KGDHt i 220.319 mmol/L Δqms 28.58 mmoL/(g·h)KPDOR i 0.418 mmol/L Δqm1,3-PD 26.59 mmoL/(g·h)KPD 25.137 h -1 ΔqmHAc 5.74 mmoL/(g·h)ms 2.20 mmoL/(g·h) As 1.896 ×10-4g/(L·h)m1,3-PD -2.69 mmoL/(g·h) K*11.43 mmol/L mHAc -0.97 mmoL/(g·h) K*1,3-PD s 15.50 mmol/L μm 0.67 h-1 K*85.71 mmol/L Ks 0.28 mmol/L Cprotein HAc 1.7 mg/mL a1 0.002 5 mmoL/(L·h)ΔUGDHtm-0.87 U/mg a2 5.18 mmoL/(L·h) ΔUPDORm-1.38 U/mg b1 0.06 mmoL/(L·h) Ks 1.35 mmol/L b2 50.45 mmoL/(L·h) Ks PDOR GDHt 2.41 mmol/L C*se 2 039 mmol/L αPDOR -1..87 U·h/mg C*1,3-PD 939.5 mmol/L αGDHt -3.53 U·h/mg C*0.14 mmol/L C*HAc 1 026 mmol/L KPDORm 0.53 mmol/L UPDORO 2.32 U/mg kPDOREtOH 360.9 mmol/L KGDHtm 0.217 UGDHtO 2.8 U/mg kGDHt 0.171 β60
2 优化模型
针对甘油生物歧化为1,3-丙二醇过程(1)~(15),本文建立了如下使主要产物1,3-丙二醇产率达到最大的稳态优化问题:
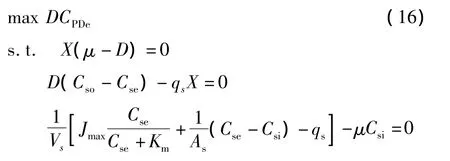

3 优化方法
针对稳态优化问题(16),本文采用约束优化方法中的内点法[22]对其进行求解。首先将问题(16)重写为如下形式:
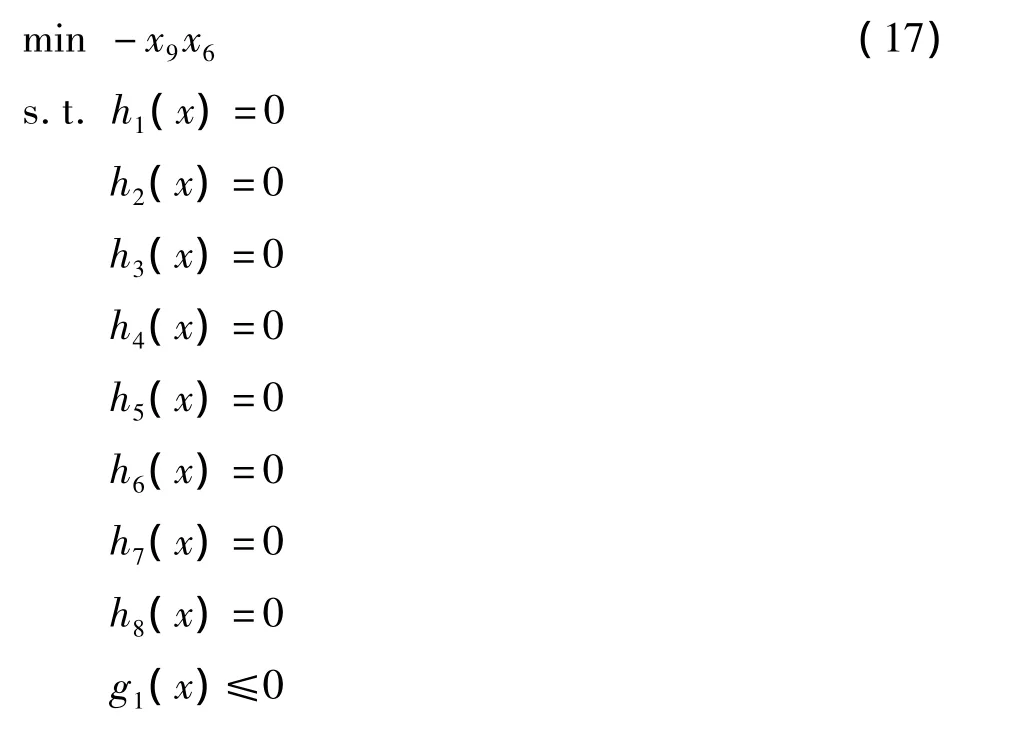
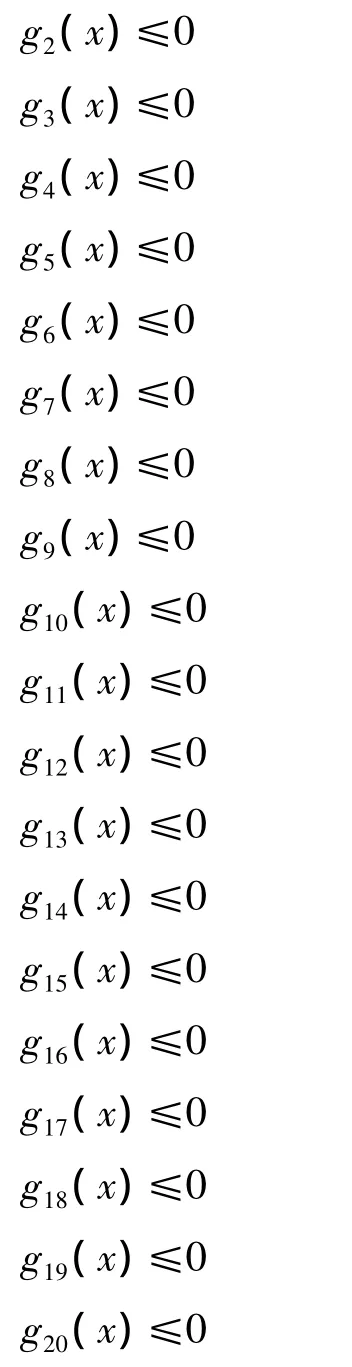
其中:

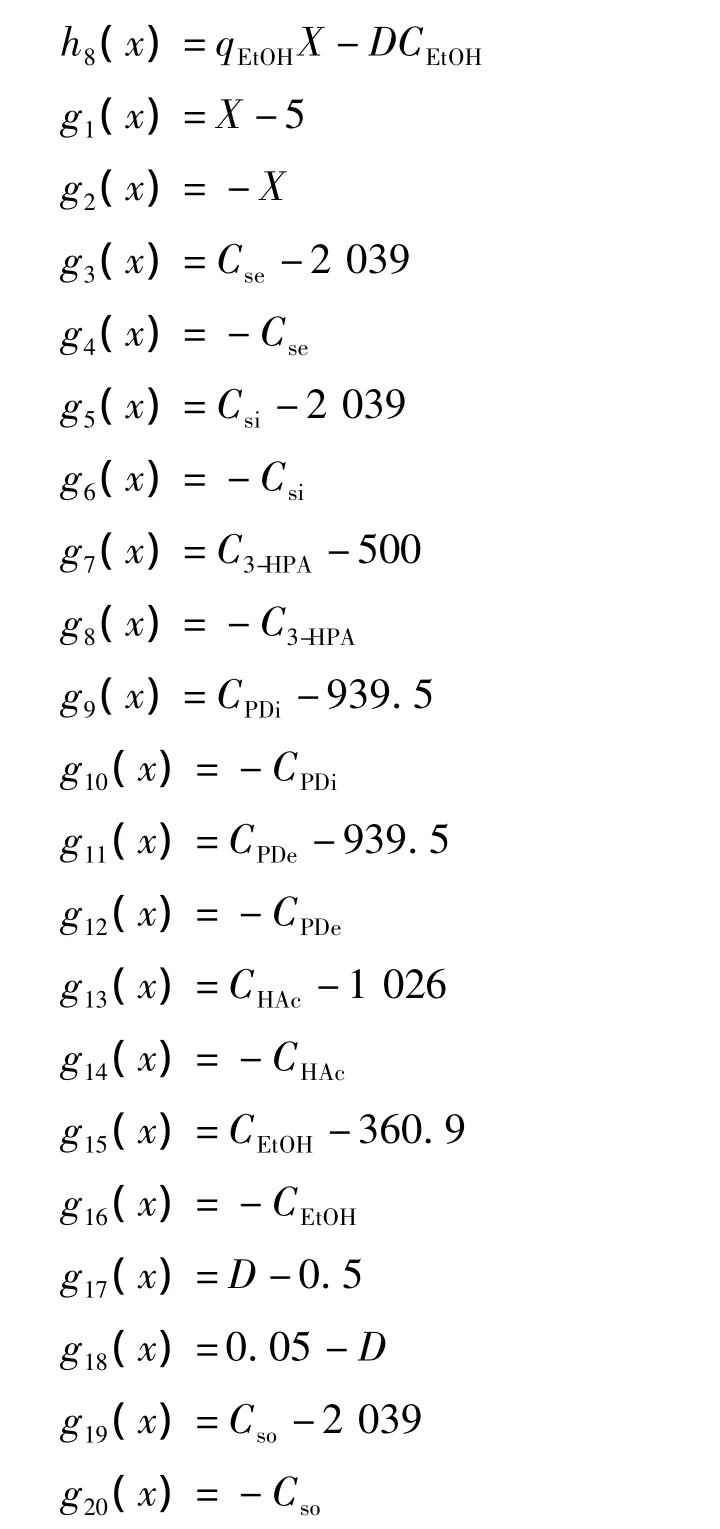
问题(17)可进一步转化为如下只含等式约束的优化问题:
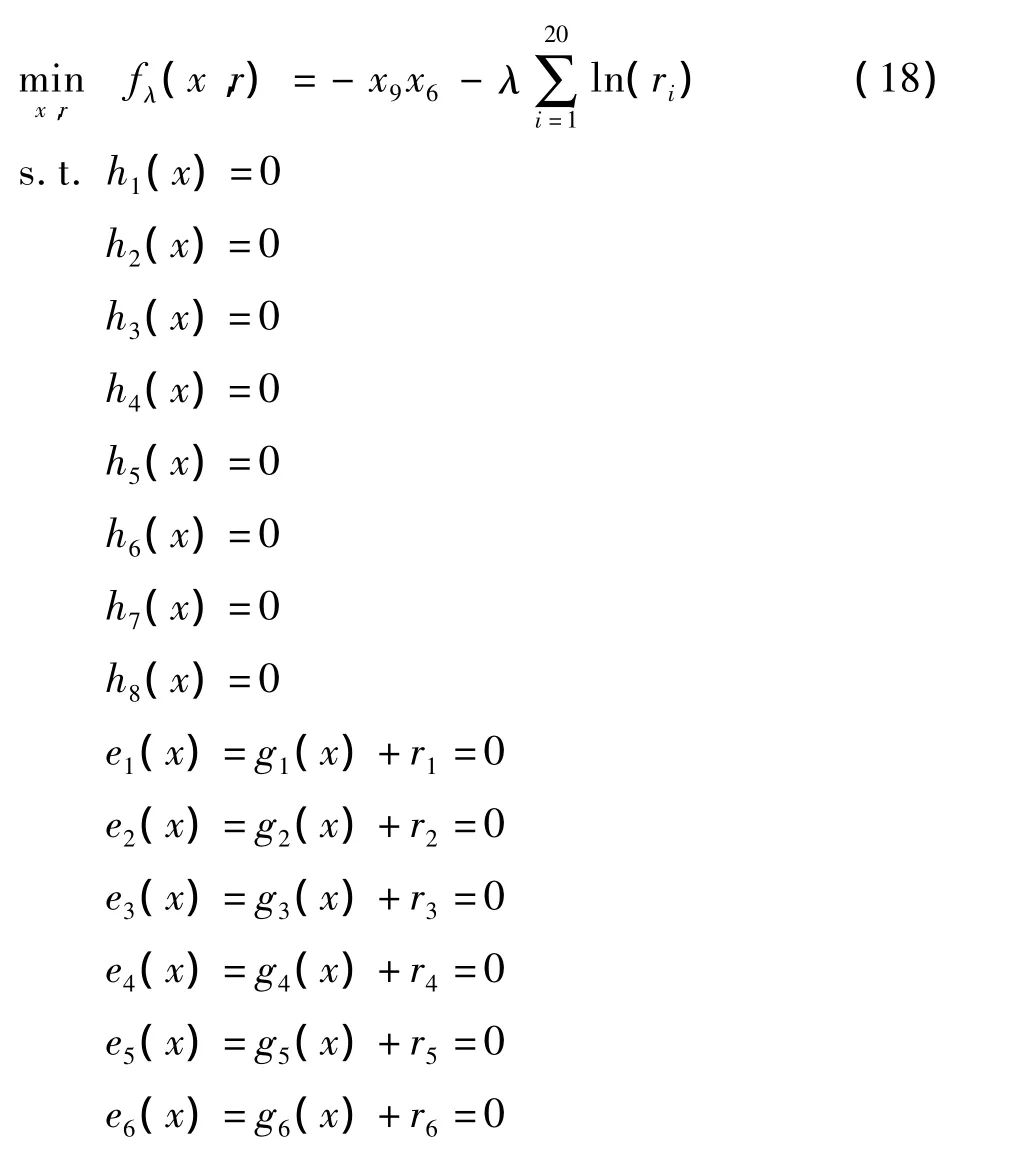

其中:r=(r1,r2,r3,r4,r5,r6,r7,r8,r9,r10,r11,r12,r13,r14,r15,r16,r17,r18,r19,r20)T。ri>0(i=1,2,…,20)为不等式约束条件的松弛变量,λ>0为障碍参数。令λ趋近于0,则问题(18)的解等价于问题(17)的解。
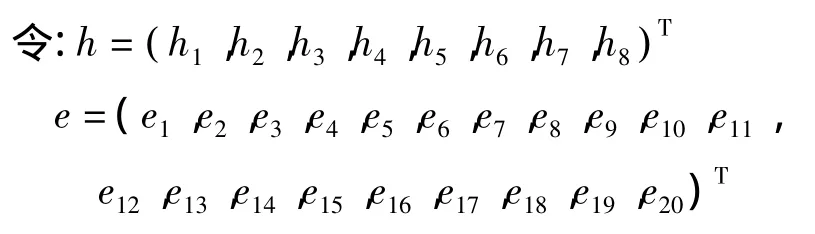
则优化问题(18)可进一步改写为如下形式:

本文应用内点算法求解优化问题(19)。
首先使用直接迭代步[22],如果不能求得最优解,则使用共轭梯度步[22]。具体步骤如下:
1)给定精度ε>0,障碍参数λ(λ>0),松弛变量 ri>0(i=1,2,…,20),初始点 x(0),令迭代次数k=0。
2)在第k次迭代时,使用直接迭代步求解无约束优化问题:

其中θ(θ>0)为参数,令其最优解为(x(k))*。
4)给定 θk+1(θk+1> θk),k=k+1,转回步骤2);若(x(k))*不能使步骤2)中无约束优化问题的 φ((x(k))*,r,θ)越来越小,则转至步骤5)。
5)使用共轭梯度步,在一个信赖域中求解步骤2)中的问题,可求得其最优解为(x(k))*。
7)令θk+1=αθk(α >0),k=k+1,转回步骤5)。
4 优化结果
本文在Matlab软件平台上应用内点法求解稳态优化问题(16),其优化结果如表2所示。从表2中可见:当稀释速率及初始甘油浓度分别为0.285 7 h-1和 730.798 7 mmol/L 时,1,3-丙二醇的最大产率为114.300 5 mmoL/(L·h)。
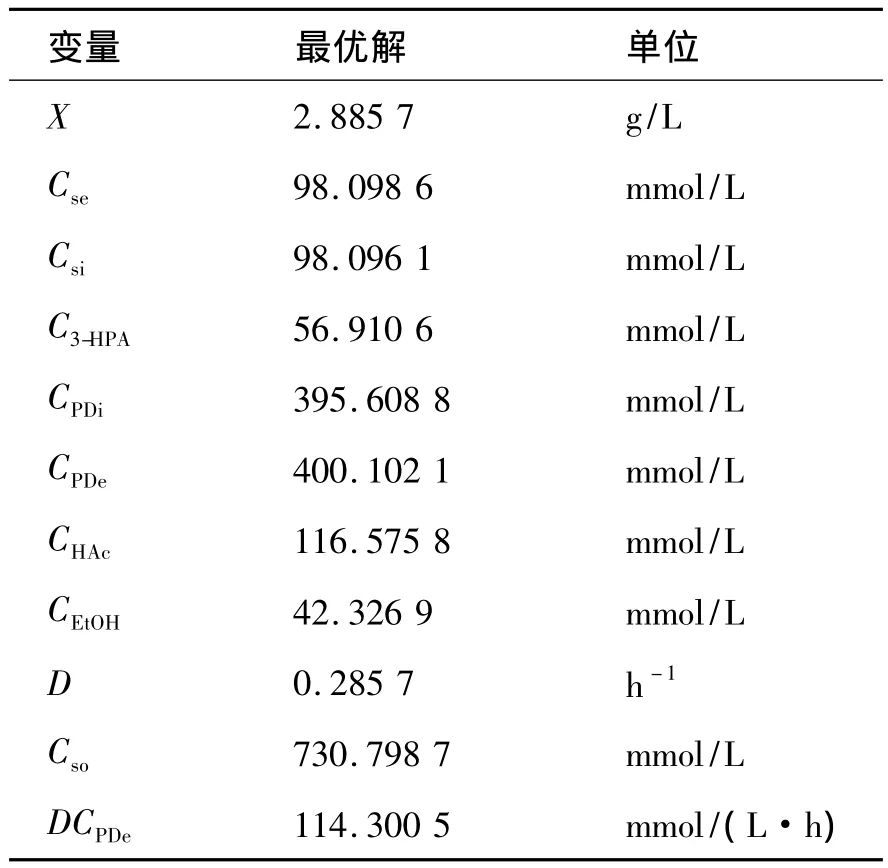
表2 优化结果
5 结束语
针对甘油生物歧化过程的稳态优化问题,本文建立了与其过程特点相适应的稳态优化模型,并利用内点法获得了生物过程的最优操作条件,取得了较好的应用效果。

附录:

续表
[1]Zeng A P,Biebl H.Bulk chemicals from biotechnology:the case of 1,3-propanediol production and the new trends[J].Advances in Biochemical Engineering Biotechnology,2002,74:239-259.
[2]Nakamura C E,Whited G M.Metabolic engineering for the microbial production of 1,3-propanedio[J].Current Opinion in Biotechnology,2003,14:454-459.
[3]Laffend A,Nagarajan V,Nakamura C E.Bioconversion of a fermentable carbon source to 1,3-propanediol by a single microorganism[J].WO96/53796,E.I.DuPont de Nemours and Genencor International,1996.
[4]徐恭贤,邵诚,钱伟懿.非线性生化过程的优化和控制[M].北京:科学出版社,2015.
[5]Zeng A P,Deckwer W D.A kinetic model for substrate and energy consumption of microbial growth under substrate-sufficient conditions[J].Biotechnology Progress,1995,11(1):71-79.
[6]修志龙,曾安平,安利佳.甘油生物歧化过程动力学数学模拟和多稳态研究[J].大连理工大学学报,2000,40(4):428-433.
[7]Gao C X,Feng E M,Wang Z T,et al.Parameters identification problem of the nonlinear dynamical system in microbial continuous cultures[J].Applied Mathematics and Computation,2005,169:476-484.
[8]Li X H,Feng E M,Xiu Z L.Stability and optimal control of microorganisms in continuous culture[J].Journal of Applied Mathematics and Computing,2006,22:425-434.
[9]Ma Y F,Xiu Z L,Sun L H,et al.Hopf bifurcation and chaos analysis of a microbial continuous culture model with time delay[J].International Journal of Nonlinear Scienc6es and Numerical Simulation,2006,7:305-308.
[10]Ye J X,Feng E M,Lian H S,et al.Existence of equilibrium points and stability of the nonlinear dynamical system in microbial continuous cultures[J].Applied Mathematics and Computation,2009,207:307-318.
[11]Lian H S,Feng E M,Li X F,et al.Oscillatory behavior in microbial continuous culture with discrete time delay[J].Nonlinear Analysis:Real World Applications,2009,10:2749-2757.
[12]张书喜.微生物发酵非线性多阶段动力系统参数辨识[D].鞍山:辽宁科技大学,2012.
[13]沈邦玉,刘重阳,叶剑雄,等.微生物连续发酵系统参数辨识与优化算法[J].大连理工大学学报,2012,52(1):150-157.
[14]李想.甘油间歇发酵酶催化-基因调控动力系统的参数辨识[D].大连:大连理工大学,2014.
[15]王艳,李晓红,冯恩民,等.微生物批式流加发酵非线性系统及其参数辨识[J].辽宁工程技术大学学报:自然科学版,2013,32(12):1704-1707.
[16]Xu G X,Shao C,Xiu Z L.Optimizing Control of Bio-dissimilation Process of Glycerol to 1,3-propanediol[J].Chinese Journal of Chemical Engineering,2008,6(1):128-134.
[17]刘颖.甘油连续生物歧化为1,3-丙二醇过程的多目标优化[D].锦州:渤海大学,2014.
[18]袁金龙,冯殊伦,冯恩民.甘油间歇发酵酶催化非线性动力系统的强稳定性[J].控制与决策,2014,29(8):1505-1508.
[19]Sun Y Q,Qi W T,Teng H,et al.Mathematical modeling of glycerol fermentation by Klebsiella pneumoniae:concerning enzymecatalytic reductive pathway and transport of glycerol and 1,3-propanediol across cell membrane[J].Biochemical Engineering Journal,2008,38:22-32.
[20]Xiu Z L,Song B H,Wang Z T,et al.Optimization of dissimilation of glycerol 1,3-paopanediol by Klebsiella pneumoniae in one-stage and two-stage anaerobic cultures[J].BiochemicalEngineering Journal,2004,19:189-197.
[21]孙亚琴.甘油生物歧化过程酶催化和基因调控的非线性数学模拟与分析[D].大连:大连理工大学,2010.
[22]Byrd R H,Hribar M E,Nocedal J.An interior point algorithm for large-scale nonlinear programming[J].SIAM Journal on Optimization,1999,9(4):877-900.

