一种基于平面对称群的对称图案生成方法

赵海英， 陈　洪， 叶瑞松

(1. 北京邮电大学世纪学院移动媒体与文化计算北京市重点实验室，北京 102101；2. 汕头大学数学系，广东 汕头 515063)

一种基于平面对称群的对称图案生成方法

赵海英1， 陈洪1， 叶瑞松2

(1. 北京邮电大学世纪学院移动媒体与文化计算北京市重点实验室，北京 102101；2. 汕头大学数学系，广东 汕头 515063)

织物图案中包含着各类蜿蜒曲线、规则与不规则的复杂元素。虽然剪纸图案和分形图案的生成方法已有大量研究工作，但是面向新疆织物图案特点的计算机自动生成方法仍然存在许多挑战性难题。针对新疆织物图案风格化建模难度大的问题，提出图案对称性作为图案生成关键指标，构造循环群和二面体群等变映射与不变映射，研究图案对称性的表征方式，利用对称图案探讨群的映射空间与对称图形之间的关联。通过群映射的仿真实验，绘制混沌吸引子得到群对称图案，有效提高图案的对称性，丰富织物图案的花型设计。

平面对称群；图案生成；迭代

新疆织物图案通过以植物生命为象征体系，展示生命与自然之美，再现各民族绘制图案的风格与特色。图案中包含大量基本元素，构成有规可循，重用性高，奠定了图案设计的良好规格。本文为了生成具有对称性新疆织物图案，构建不变映射和等变映射f(x; y)的动力系统，绘制其轨迹的混沌吸引子图案保持平面晶体群的对称性，依此设计具有对称性与风格化的图案。而图案生成取决于能否将现有信息技术与手工艺设计、现代设计理念相结合，设计出保留风格的传统图案是具有挑战性的问题。目前，在设计领域开放性的问题有：①图案底层特征、风格特征描述；②图案生成规则；③传承民族风格的图案设计方法。

1　相关工作

艺术设计工作中很大一部分工作是艺术图案设计，从理论上深入研究各种图形的性质和规律，也就是用数学的方法研究图形[1]。在实际工作中也常常是把绘图和计算相结合，即所谓形数结合。实践证明：任何一个图形，都可以用数学方程表示、讨论；反之，数学问题也可以用图形来描绘。这就为形与数结合奠定了理论基础[2]。

对称性是自然界普遍存在的现象。新疆少数民族在地毯、挂毯、墙壁等装饰和建筑上普遍使用。理论上，一个系统如果是对称的，那么在数学上反映为该系统具有群作用下不变的特性，而在集合上反映为集合对应的图形之间的关系[3-4]。

Field和Golubitsky[5]研究了混沌与动力系统的共存关系，生成具有晶体群、二面体群和循环群作用下的对称性混沌吸引子，并借助颜色绘制方法生成了具有群对称的混沌吸引子。Lu等[6-7]在文献[5]的基础上，利用“轨迹井”技术和新调色板技术生成了具有晶体群对称性和循环群、二面体群对称性的艺术图像；王兴元和石其江[8]生成了广义M-J集分形艺术图像；Chung等[9-11]从动力系统观点出发研究了平面上的“penrose tilings”和“fractal tilings”等艺术图像构造的方法和理论；邹玉茹等[12]利用p4晶体群等价函数通过探讨图形拼砌边界无缝隙条件构造了“chair tilings”非周期艺术图像；之后，Lu等[6]从动力系统角度研究了群对称性不变函数的理论，并引入色彩对称映射构造了晶体群对称艺术图像，克服了轨迹井技术对“滑动反射”可能失效的缺点。

Carter等[13]构造平面上具有对称性和周期性的三角函数族，生成平面上7种带群(frieze groups)和17种晶体群(wallpaper groups)[4]，其中17种晶体群用传统的记号标记为p1，p2，pm，pg，pmm，pmg， pgg，cm，cmm，p3，p3m1，p31m，p4，p4m，p4g，p6，p6m。平面晶体对称群也称为壁纸群(wallpaper group)，该类群由两个方向的周期性变换和镜面反射、平移反射、旋转对称相互作用形成。

传统生成具有平面晶体群对称图像的方法大都是手工绘制[3-4]，文献[14]采用计算机自动生成该类拼砌图像，生成的图像是黑白混沌吸引子图像。Chung和Chan[15]通过Monte-Carlo搜索产生随机的动力系统，并通过计算系统的 Lyapunov指数寻找平面对称混沌吸引子轨迹，并利用颜色井生成彩色拼砌图像。

图案设计是计算机应用领域的一个崭新的、最活跃的、应用面最广的、对国民经济建设有着重大作用的一个重要分支[16-17]。新疆民族织物图案的组成比较复杂，花型多、时空跨度大、风格各异，这使得图案很难用传统的曲线或曲面描述，给图案特征分析与自动生成造成很大困难。吸纳已有图案设计和生成经验，将会有助于图案设计方法的提出。

2　基于平面对称群图案生成映射构建

利用对称混沌吸引子进行计算机绘制，可以保持图案具有对称性，其理论依据是文献[18]提出的函数等变性定理。

定理. 设f:R2→R2是任意一个函数，G是一个由 2×2矩阵构成的有限群，则函数hf(x)=

具有群G的等变性。

证明：令γ∈G，则：

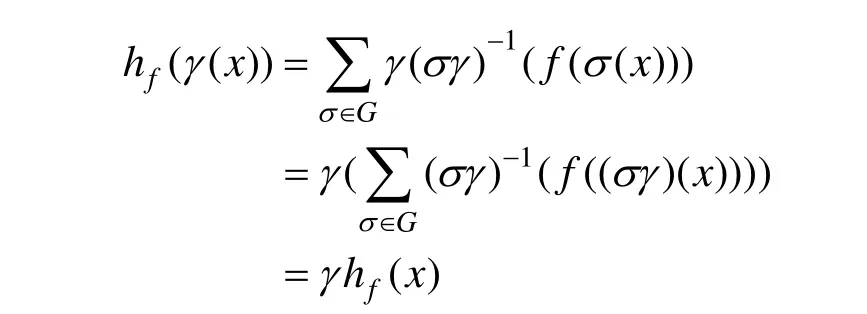
由群的封闭性可知，当σ跑遍整个群时，σγ也跑遍整个群。

文献[18]提出的定理好处在于充分利用群的封闭性，函数的选择比较随便，减少了为保证函数具体等变性所进行的复杂构造过程。本文通过构建具有平面对称映射的动力系统来绘制混沌吸引子图案，得到对称图案。下面构造循环群 zn和二面体群Dn等变映射，实现对称性图案绘制。

2.1构建基于循环群zn映射

(1) 对于 zn群，设f(z)为复平面上的映射。构造如下映射，满足基于循环群的等变映射：

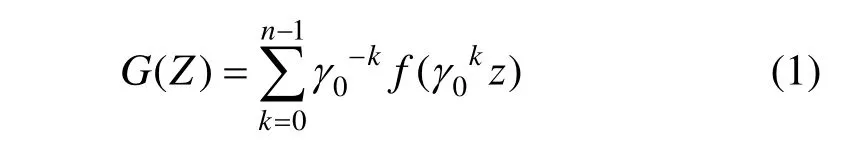
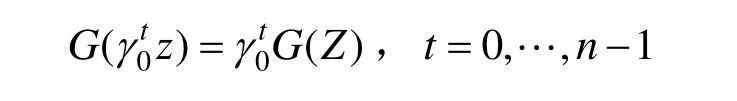
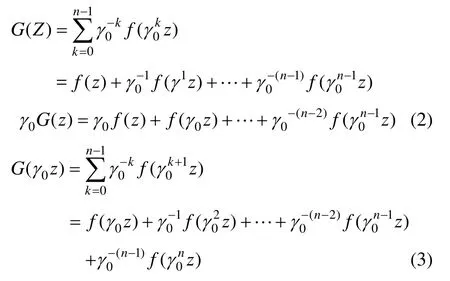
比较式(2)、(3)可知，只需要证明γ0f(z)=即可。

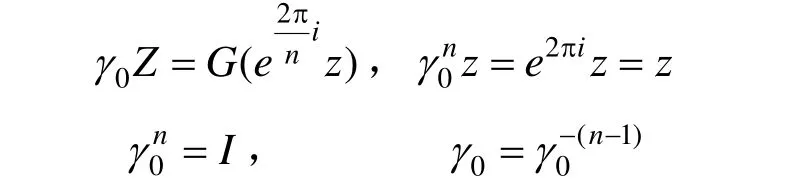
(2) 构造如下映射，满足基于循环群的不变映射：

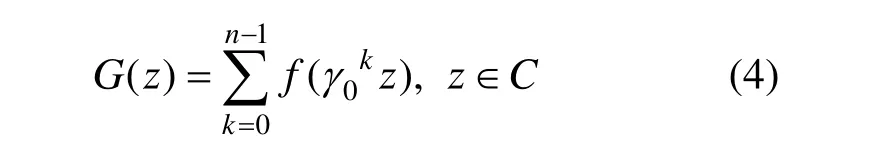
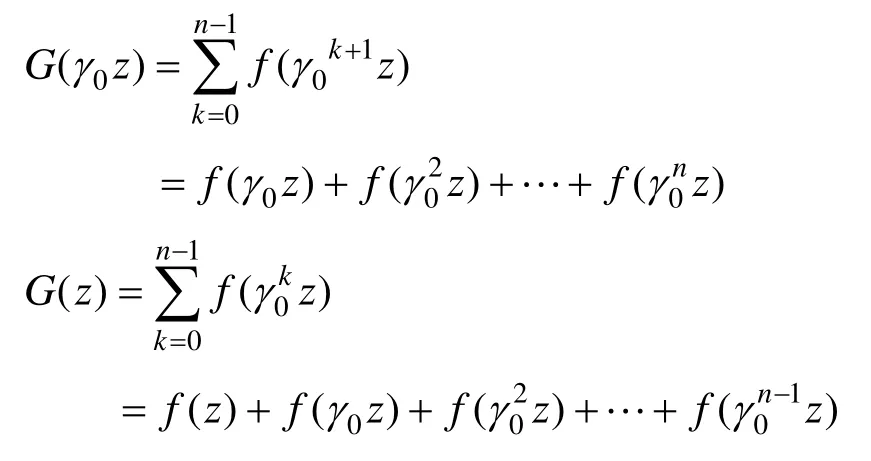
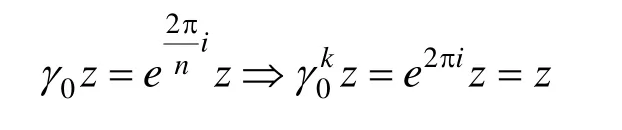
2.2构建基于二面体群Dn映射

(1) 对于Dn群，设f(z)为复平面上的映射，构造下面的映射，满足基于二面体群的等变映射：

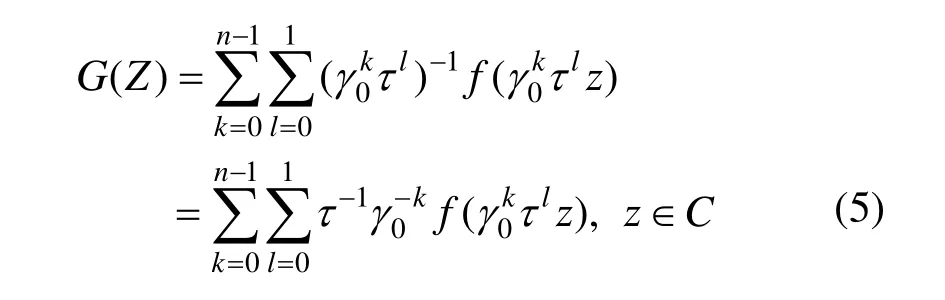
证明：当t=1,s=0时，只需证明：G(γ0z)=γ0G(z)。

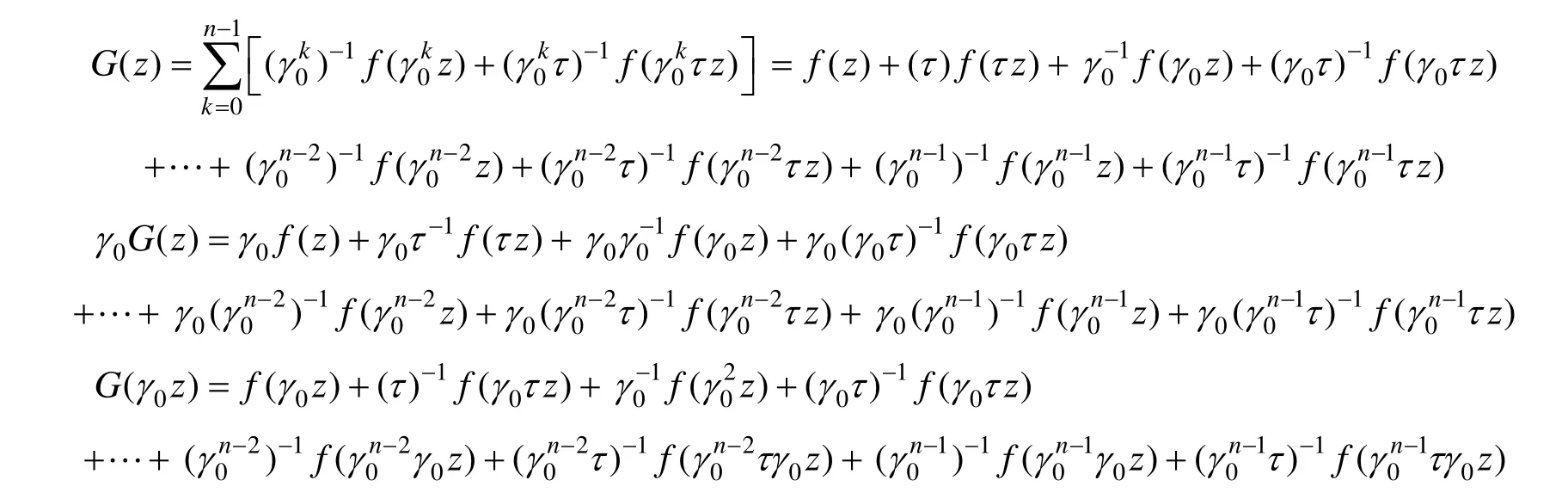
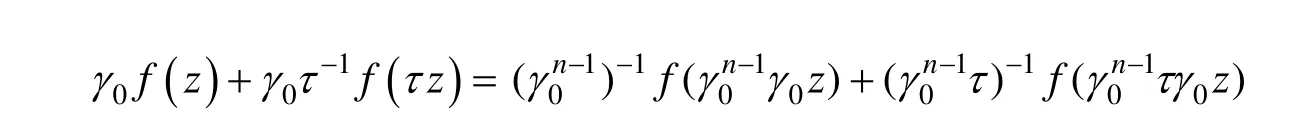
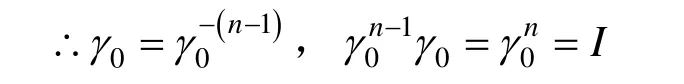
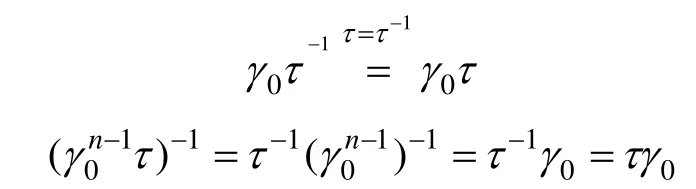
即求证γ0τ=τγ0，由二面体群性质知：

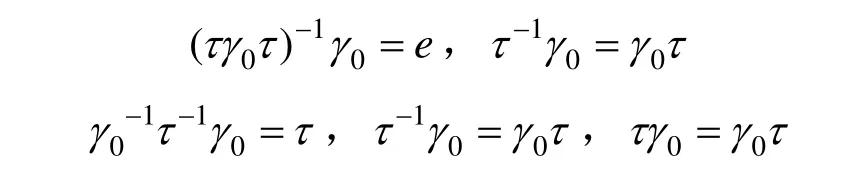
(2) 构造下面的映射，基于二面体群的不变映射：

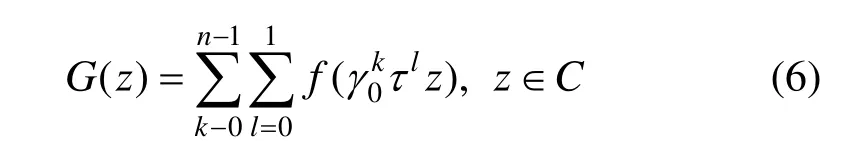
同上定理可证：

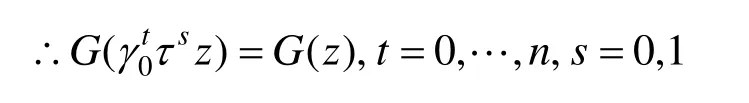
3　平面对称群对称图案生成仿真实验

设f(z)=z=x+iy，分别按照式(1)、(4)～(6)进行G（z）的绘制，即可得到不同对称图案。

绘制对称图案过程描述如下：

步骤1. 选定一个初始点(x,y)及迭代次数N；

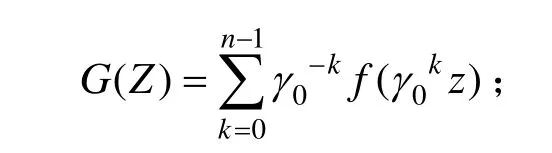
步骤3. 令x=xnext，y=ynext;

步骤4. 如果迭代超过100次, 则屏幕输出(x,y)；

步骤5. 返回步骤执行下一轮迭代，直到迭代次数等于N次。

根据仿真实验步骤，分别基于循环群和二面体群完成不同对称映射拼贴，如图1和图2所示。

4　不同对称图案生成方法分析

4.1不同非线性系统生成方法仿真实现

新疆少数民族织物图案以抽象的植物纹样和几何纹样为主表现，为此提出非线性系统生成织物图案进行分析对比。

实验1. 基于L系统的服饰图案生成

L系统是一类独特的迭代过程，与迭代函数系统(iterated function system，IFS)一样是分形物体常用的模拟工具，也是非常有效的生成方法，是目前用于模拟分形物体最常用、最成功的系统。使用时定义一个有序的三元组：其中符号集α为旋转角，起始符号元ϖ。而最关键的是生成规则集p的选择，可根据图案的对称特点进行设置。依据新疆民族织物图案特点，选择变换规则集及迭代次数n。确定参数绘制基于L系统的不同织物图案，如图3所示。

实验2. 融合IFS迭代函数与L系统生成图案

研究考虑到新疆织物图案多是植物形状，将IFS生成算法和L系统结合。根据拼贴定理，对于任意原始集L，只要能保证L与拼贴的W(L)之间较好地符合，其吸引子就一定接近于原始图形。通过IFS与L系统的结合，可绘制出如图4所示的分形植物。

仿真实验可以发现，IFS主要应用于分形植物叶片模拟，也可用于艺术分形图的生成；而L系统法虽能极为逼真地模拟自然界中部分景物，如上图的枝茎，但其绘制必须要知道生成图案的初始生成元和迭代规则，实际操作较为困难。

实验3. 基于模糊元胞自动机演化算法

把专家知识先转换成数学形式，然后加以应用。通过符号自然语言表达式，转换成数学函数。加入领域专家知识的图案更具民族风格。论文引入模糊系统改进元胞自动机得到模糊元胞自动机。模糊元胞自动机模型(fuzzy cellular automata)是在平面上用一个M×M的格点组成网格矩阵来表示的，已知每一个格点t时刻状态，(t+1)时刻状态由X(t)时刻自身状态、周围邻元状态以及模糊规则来决定。其中模糊规则中的隶属度函数是最关键的问题，如图5所示。由于新疆民族织物图案花型复杂性，在应用 FCA时，不仅要考虑模糊规则，还要考虑其初始构型。

图1　基于循环群不同对称映射拼贴结果

图2　基于二面体群不同复映射拼贴图案结果

图3　基于L系统织物图案

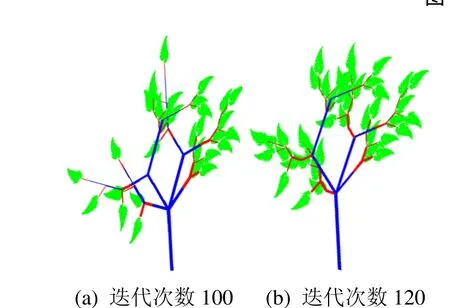
图4　植物纹样建模

4.2基于非线性系统生成方法的比较

(1) 分析以上3种非线性系统生成图案算法，其共性：①生成图案极具规则，且生成元与生成规则或演化规则的泛化能力极弱；②从实物图案中寻找生成规则难度大，致使迭代函数系统参数难以确定。

(2) 分别实现了分形IFS和L系统以及一维元胞演化模型，但是仿真结果表明：生成的图案只能是极具分形特征的相似图案，其数量非常有限，而且建模过程依赖于生成元或演化规则即图案基元，不能满足设计者对具有新疆风格的图案设计要求。

(3) 仿真实验表明分形图案虽体现出传统美学的标准，如平衡、和谐、相似等，甚至局部与局部之间、局部与整体之间也存在绝对的自相似，但完全不同于织物图案的对称和谐，对称中有变化，变化中有和谐；而IFS系统和元胞演化模型生成过于简单相似，难以满足新疆织物图案设计目标。

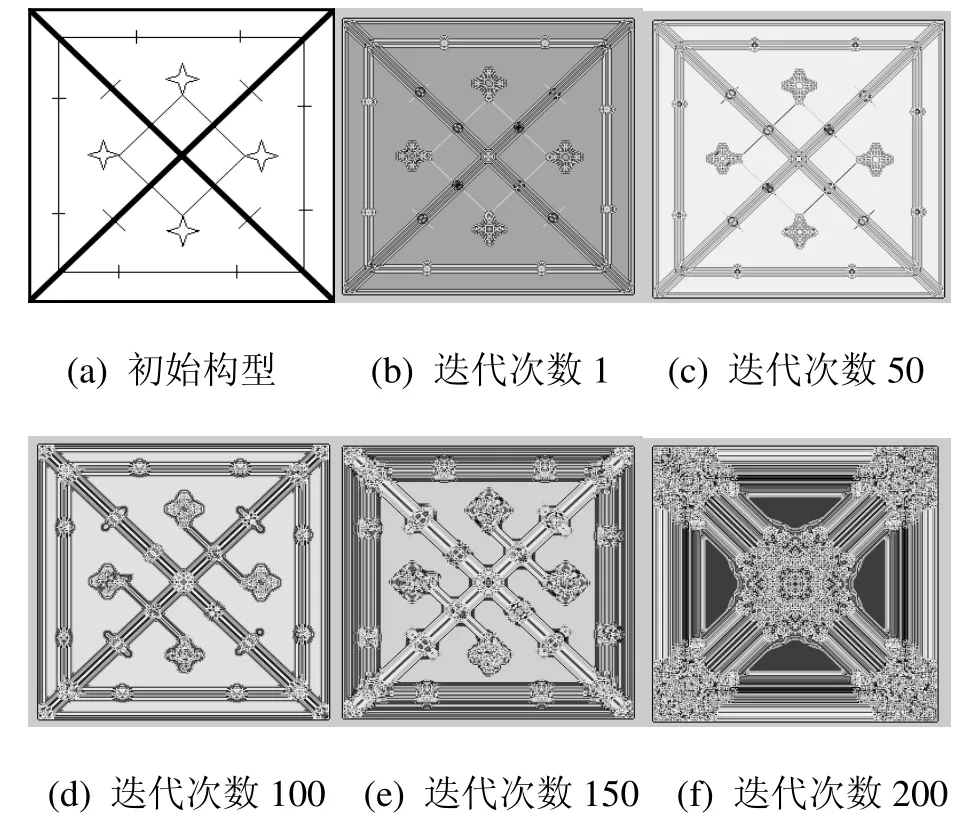
图5　元胞在不同迭代次数下演化过程

为此，引入平面对称群构建映射生成对称图案，即通过构建具有平面对称映射的动力系统来绘制混沌吸引子图案，可具有变化对称性。

5　小　结

分形图在服装设计上的运用体现出计算机科学、数学、服装美学等的完美结合，传达出一种全新的视觉效果。为此，在迭代函数系统的研究中，从线性IFS推广到元胞自动机演化模型，再进一步推广到混沌吸引子构建的迭代函数系统，目的在于绘制风格化织物图案。但由于系统构建的复杂性，模型演化不可预测性，使得生成图案虽具有对称性，但与民族特色仍具有较大差距。因此，提出面向风格化的图案生成算法仍然是最具挑战性问题。

本文采用循环群和二面体群的等变和不等变映射，研究迭代混沌吸引子的轨迹生成对称图形，该方法可以绘制具有对称特征图形，并通过颜色表进行图案渲染，得到色彩绚丽对比度强的对称图案。但图案特征的定量计算仍然需要进一步深入研究；基于进化计算的图案生成方法也可以引入，因为图案智能化和走向应用是设计的目标。

[1] Schnier T, Yao X, Beale R, et al. Nature inspired creative

design-bringing together ideas from nature, computer science, engineering, art, design [C]//Proceedings the Seventh International Conference on Adaptive Computing in Design and Manufacture (ACDM2006), Bristol, UK, 2006: 237-240.

[2] Ullman D G. The mechanical design process [M]. 2nd ed. New York: Mc-Graw-Hill, 1997: 315-322.

[3] Grunbaum B, Shephard G C. Tilings and patterns [M]. 2nd ed. Cambridge: Cambridge University Press, 1963: 369-372.

[4] Armstrong M A. Groups and symmetry [M]. New York: Springer-Verlag, 1988: 155-164.

[5] Field M, Golubitsky M. Symmetry in chaos: a search for pattern in mathematics, art and nature [M]. SIAM, 2009: 98-101, 151-158.

[6] Lu J, Ye Z, Zou Y. Automatic generation of colorful patterns with wallpaper symmetries from dynamics [J]. The Visual Computer, 2007, 23(6): 445-449.

[7] Zou Y, Li W, Lu J, et al. Orbit trap rendering method for generating artistic images with cyclic or dihedral symmetry [J]. Computers & Graphics, 2006, 30(3): 470-473.

[8] 王兴元, 石其江. 拟3D的广义MJ集[J]. 计算机辅助设计与图形学学报, 2006, 18(11): 1683-1690.

[9] Chung K W. Automatic generation of aesthetic patterns on a periodic tiling by means of dynamical systems [J]. International Journal of Bifurcation and Chaos, 2004, 14(9): 3249-3267.

[10] Chung K W, Ma H M. Automatic generation of aesthetic patterns on fractal tilings by means of dynamical systems [J]. Chaos, Solitons & Fractals, 2005, 24(4): 1145-1158.

[11] Chung K W, Chan H S Y, Wang B N. Automatic generation of nonperiodic patterns from dynamical systems [J]. Chaos, Solitons & Fractals, 2004, 19(5): 1177-1187.

[12] 邹玉茹, 李文侠, 鲁坚. Chair Tilings非周期艺术图案的生成[J]. 计算机辅助设计与图形学学报, 2006, 18(4): 498-501.

[13] Carter N C, Eagles R L, Grimes S M, et al. Chaotic attractors with discrete planar symmetries [J]. Chaos, Solitons & Fractals, 1998, 9(12): 2031-2054.

[14] Field M, Golubitsky M. Symmetric chaos [J]. Computers in Physics, 1990, 4(5): 470-479.

[15] Chung K W, Chan H S Y. Symmetrical patterns from dynamics [C]//Computer Graphics Forum. Blackwell Science Ltd, 1993, 12(1): 33-40.

[16] 刘弘, 刘希玉, 唐明晰. 支持外观造型创新设计的计算机辅助设计环境[J]. 计算机辅助设计与图形学学报, 2003, 15(10): 1258-1262.

[17] 黄墒, 孙守迁, 张立珊. 面向产品创新的3维草图设计技术研究[J]. 计算机集成制造系统, 2007, 13(2): 224-227.

[18] Dumont J P, Reiter C A. Chaotic attractors near forbidden symmetry [J]. Chaos, Solitons & Fractals, 2000, 11(8): 1287-1296.

Generation Method of Symmetrical Pattern Based on the Plane Symmetry Group

Zhao Haiying1,Chen Hong1,Ye Ruisong2
(1. Mobile Media and Cultural Calculation Key Laboratory of Century College, Beijing University of Posts and Telecommunications, Beijing 102101, China; 2. Department of Mathematics, Shantou University, Shantou Guangdong 515063, China)

Fabric design is a kind of complex texture pattern, with winding curve, regular and irregular geometrical patterns as the main pattern. Although the pattern generation methods of paper-cut design and fractal pattern have a lot of research work, the computer automatic generation method for fabric design characteristics in Xinjiang still exists many challenging problems. Considering the difficulties of stylized model building of Xinjiang fabric pattern, the method that uses pattern symmetry as the key index of pattern generation is proposed, build the variable and invariable mapping of cyclic group and dihedral group, study the representation of pattern symmetry, prob the relationship between mapping space of group and symmetric graph using symmetric patterns. Through the simulation experiment of mapping group, the symmetrical design with chaos attractor is drawn. Experiments show the generation method can improve the symmetry of pattern and rich the pattern design of fabric.

plane symmetry group; pattern generation; iterative

TP 391

A

2095-302X(2015)06-0872-07

2015-02-05；定稿日期：2015-07-08

国家自然科学基金资助项目(61163044)；北京市科委资助项目(Z141100001914035)；国家社科基金重点项目(12AZD120和12AZD118)；新疆自然科学基金资助项目(2010211a19)

赵海英(1972–)，女，山东烟台人，副教授，博士。主要研究方向为文化计算和媒体数据挖掘。E-mail：zhy.yn@163.com

陈洪(1976–)，男，四川达州人，副教授，博士。主要研究方向为计算机图形学与数字媒体技术。E-mail：norman_chen@263.net