管道内壁全景图像自适应展开算法研究

唐爱平

(常州纺织服装职业技术学院创意与艺术设计学院，江苏 常州 213164)

管道内壁全景图像自适应展开算法研究

唐爱平

(常州纺织服装职业技术学院创意与艺术设计学院，江苏 常州 213164)

全景环形透镜(panoramic annular lens)是一种特殊的光学成像器件，将其应用在管道形貌检测领域，恰好能忽略管道径向上的中空图像且能获取整个管道内壁一定范围内的全景图像。吸收传统展开算法中切向展开的优点，设计一种标定实验，利用边缘提取、Hough变化、插值等方法来自适应地调节映射点领域内的权值，达到圆环的自适应径向展开。仿真实验表明，该算法有效地改善了径向放大率，方便适用于不同管径管道。

全景图像；径向展开；自适应；仿真

全景环形透镜(panoramic annular lens，PAL)的问世，使得360°成像成为可能，其通过平面圆柱投影法(flat cylinder perspective，FCP)将三维现实空间中的景物投影至一个环形区域内[1]。自上个世纪80年代起，国际上就兴起了对全景成像系统的研究，并将此类系统应用到不同的场合中。至今，全景环形成像系统已在航空航天、机器视觉、视频监控，视频会议及工业管道检测等领域取得了一定的成果[2-3]。

利用 PAL无需添加任何旋转模块便可实现管道内壁一定范围的360°成像，在保证图像质量的同时，加快了处理速度[4]。对于管道内壁所成的全景环形图像需要利用展开算法对其进行处理，方便后期对管道内壁形貌的分类识别。

在PAL图像展开算法中，基于图像映射的线性展开算法[5-6]为最常见的一种。其算法的核心思想是将环形图像中的外圆周和内外环半径差分别作为展开矩形的长和宽，由于内圆环半径小于外圆周，导致分辨率不足，为了保证各圆周拥有相同的分辨率，故对非外圆周图像进行展开时通过插值等方法来提高其分辨率[7-8]。在实际情况下，这类展开算法主要适用于管径固定的管道检测，虽然通过曲线拟合的方法可以精确地恢复出柱面原貌，但在柱体半径变化情况下，这种展开是不可取的[9-10]。

本文针对传统的展开算法中存在的问题，提出一种自适应径向展开算法，在自适应矫正径向放大率的同时，能够实现对不同管径管道内壁全景图像的展开。

1　基于图像映射的自适应展开算法

PAL图像展开算法的思想是将环形图像中的外圆周和内外环半径差分别作为展开矩形的长和宽，分为2步：①切向展开，即以环形图像的外圆周的周长及周围的分辨率，将环形图像展开为矩形图像，保证尺寸最大化的同时确保分辨率最高；②径向展开，由于PAL图像采用的是FCP投影法，其遵循f−θ理论，柱面上等距的环线在环形图像中随着圆环半径的增大，圆环之间的距离也越大，故需要对已进行切向展开的图像进行径向上的拉伸[8]。然而由于内圆环半径小于外圆周，导致分辨率不足，为了保证各圆周拥有相同的分辨率，故对非外圆周图像在展开时运用插值等方法来提高其分辨率，达到径向方向上无畸变的需求[11]。

1.1全景图像切向展开

假设摄像头中心与管道中心同一径向，进行切向展开时，根据已知PAL环形图像的中心对其进行展开，将外圆周的周长作为展开图像的长度，内外圆的半径差作为展开图像的宽度。在展开过程中(如图1所示)，设p点在展开图像中的坐标为p(x,y)，其在环形图像中所对应的点用极坐标表示为p′(x′,y′)，将环形图像用其原点的极坐标f(ρ,θ)表示：

图1　坐标转化示意图

式(1)中，(x0,y0)为圆心在直角坐标系中的坐标；点A为过圆心O与x轴平行的直线与内圆环相交的点；其与圆心的距离为内环半径r；θ角为0；其在环形图像中的坐标为A(x0+r,y0)。因为展开后矩形图像的y轴为环形图像的内外半径差，x轴为环形图像的外圆周长，所以在展开图像中 p点与A点在y轴方向上的差即为ρ与r的差值，在x轴方向上的差为 θ角在外圆周上弧长，得到如下公式：

其中，点 A在展开图像中的坐标为(xA,yA)，为了便于计算，将点A平移至展开矩形图像坐标系的原点，式(2)可简化为：

将式(3)代入式(1)得到展开矩形图像中每个点在环形图像中所对应的坐标：

至此，通过坐标转化可将展开后的矩形图像中的点与原有环形图像中的点一一对应。虽然通过上述的展开后，图像已经趋近于真实的图像，但在径向上还存在分辨率不足的问题，需要对径向方向上进行拉伸。

1.2全景图像径向自适应插值算法

全景图像径向拉伸通常使用最小二乘曲线拟合的方法对图像进行拟合，这需要有标准的参考图进行恒定，才能找出拟合图像与实际图像之间的对应关系。这种展开算法主要适用于固定管径的管道检测，无法实现对不同管径的展开。

对于切向方向，PAL具有旋转不变性，即在切向方向上各个点之间的放大率相同，而在径向方向上存在着畸变。对于相同距离的物点，径向上的放大率沿着径向方向递减，出现近大远小的畸变现象。根据本文的实际情况，针对不同管径的圆柱形管道进行形貌检测，在基于图像映射的线性展开算法上进行改进，提出自适应插值展开算法，来消除不同管径径向上的畸变。

根据式(1)原始图像中的点p(x,y)经过切向转换后坐标为而期望得到的展开图像对应的坐标为两者之间存在以下关系：

为了得到p′坐标，在圆柱形管道直径发生变化时，需要根据图像映射点领域内的灰度值变化情况，即根据点p′(x′,y′)周围领域内灰度值的变化情况，将映射点的直接邻接点与其间接邻接点梯度的比值作为λ值的判断依据，以此满足不同管径的全景图像，并确定径向展开的表达式。

根据切向展开后的映射点p′(x′,y′)，可以认为插值后像素值 pi′的坐标为(x′,y′)，i表示映射点图像的序列号。切向展开后图像的插值像素点与其邻近像素点的位置关系如图2所示。

图2　插值点与邻近映射点的位置关系

当(x−,y−)、(x−,y+)、(x+,y−)和(x+,y+)4个邻近点区域的标记相同时，表示λ的取值满足需求，否则对其自适应进行调整。定义图3中映射点i的梯度为：

图3　插值点有邻近点灰度关系图

在进行径向展开时，λ的取值由下面梯度区间决定：

实验表明，通过本文提出的自适应插值法，能按照相邻切向上两个交点的距离进行插值拉伸，可以很好地消除径向上的畸变，达到圆环图像的无损展开。

2　管道全景环形图像的圆心标定校准

上述展开算法以所成图像的中心作为理想的展开中心，然而在实际图像中可能存在中心偏移的问题。当存在偏移时，仍然以几何中心作为环形图像的展开中心来进行展开的话，得到的展开图像将存在着弯曲的现象[12-13]。故此，在展开之前，通过圆心标定校准来寻找正确的展开中心，即全景图像上管道内壁所形成的同心圆圆心，可以极大地减少后期全景图像展开误差。

针对管道的实际全景图像特点，即管道内壁形成的图像为同心圆，提出一种快速圆心检测方法。将图像空间转换成为由圆心横坐标、圆心纵坐标及半径所组成的3个参数空间。参数空间对应的量化值分别为Δr ， Δx， Δy，这3个量化值将整个参数空间分成很多个量化空间，即每一个量化值对应了一种圆心半径的量化空间，其在立体空间上是一个长方体也可称之为“盒子”。满足同一圆心，同一半径的圆环曲线上的像素点坐标都放在同一个“盒子”中。比较所有“盒子”中像素点个数，个数最多的那个“盒子”的3个参数即为圆检测的最优参数。整个参数空间中“盒子”的总数由3个参数的范围及量化值决定，如式(8)：

为了确保圆检测的精度，3个量化值的范围必须取得尽量小，一般为1～2个像素点，在本实验中设置为1个像素点，圆检测的数据量就由3个参数的取值范围所决定。通过对3个参数的取值进行约束，缩小其取值范围就能大大减小其中的数据量，实现快速检测，且能保证圆心的精度。算法步骤如下：

步骤1. 获取标定图像的环形图像如图4所示，并对获取的环形图像进行边缘提取，获得内环，外环，及中环3个同心圆。

步骤2. 由于内环的边缘是最小的一个圆(简称为内圆)，设内圆在x轴方向上最右端的像素点的坐标为(xr,yr)，最左端的像素点坐标为(xl,yl)，则两点间x轴上的距离为w=xr−xl，在y轴方向上最上端的点的坐标为(xu,yu)，最下端的点的坐标为(xd,yd)，两点在y轴上的距离为h=yu−yd。估计内圆的圆心在附近，且半径也应该与(或)相当。为此，内圆的3个参数取值范围分别如下：

设置 δ1=10， δ2=10(δ1表示圆心坐标的允许误差， δ2表示圆环半径的允许误差)，对内圆进行边缘提取及Hough变换，检测标定得到的圆心坐标为(x1,y1)。

步骤 3. 同理，可以通过计算获取外环及中环圆的圆心坐标，取三者的平均来确定这个管道内壁图像的同心圆圆心。

3　实　验

本文基于PAL的成像原理和特点，采用搭载全景镜头的爬行器对管道内壁进行图像采集，其结构如图4所示。根据前文提出的全景图像圆心标定及自适应展开算法，对管道内壁的全景图像进行展开，验证本文算法的正确性，实验结果如下。

图4　管道内壁全景图像采集结构图

按图 4结构搭建实验平台，获取的全景图像如图5(a)所示，中心坐标为(741,975)，根据式(8)、(9)，采用边缘提取算法确定各个圆环的圆心坐标如图5(b)及表1所示。

图5　圆环圆心标定图像

表1　各圆环圆心坐标及半径

从表1可知，各同心圆环坐标分别为(741,973)，(741,977)，(745,977)，其圆心均值为(742.3,975.7)，误差δ1=1.3， δ2=0.7在标定范围内。

校准圆心坐标后，采用式(6)、(7)对切向展开图像(图6(a))自适应调整梯度差值，经过边缘提取(图6(b))，Hough变换(图6(c))获得径向展开后的图像，如图6(d)所示。

图6　径向展开实验

经过Hough变换提取直线交点位置信息(x坐标为水平方向，y坐标为垂直方向)，部分交点数据如表2所示。

根据表2的交点数据，计算切向展开图像相邻两点之间的距离，结果如图7所示。

从图6中可以看出，本文所提出的径向展开算法能很好地提取标定网格直线边缘且能准确地找到网格直线的交点。通过分析切向和径向上相邻交点间的数据，如图7，相邻交点切向间距基本一致，图中所出现的拐点是由于原图中径向上存在两条相近的直线导致，而从图8中可以明显看出各行之间的径向间距存在着拉伸。通过本文提出的自适应展开算法使得径向上具有切向上的放大率，达到消除畸变的目的。插值后同样获取网格直线的交点，部分数据如表3所示，展开前后各行径向间距对比如图9所示。从实验结果中也明显看出径向展开后，拥有相同的径向间距。

表2　切向展开图像部分交点坐标数据表

图7　切向展开图像相邻交点切向间距

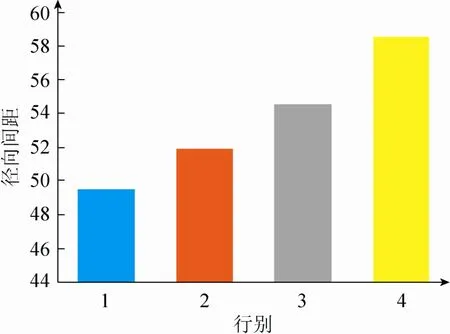
图8　切向展开图像各行径向间距

图9　径向展开前后各行径向间距对比图

表3　径向展开后部分交点坐标数据表

4　结　论

文中提出一种管道内壁全景图像自适应插值展开算法，结合传统展开算法中切向展开的优点，改进径向展开算法，从而自适应地对不同管径的管道内壁全景图像进行展开。实验验证了改进的径向展开算法能很好地保证径向上的放大率，且无需人工提取标定参数，从而能自适应不同管径的管道。当前检测系统的硬件平台只能满足在直管道中进行检测且对于管道的直径有一定的要求，通过调整爬行器的机械结构使其满足不同直径的管道需求，考虑在硬件平台上加装传感器，使其能适应带有弯道的管道，且如何重构弯道管道图像将是后续研究的方向。

[1] 赵玮芳. 超高像素全景环带成像研究[D]. 杭州: 浙江大学, 2007.

[2] Kopilovic I, Vágvölgy B, Szirányi T. Application of panoramic annular lens for motion analysis tasks: surveillance and smoke detection: pattern recognition [C]//IEEEProceedings. 15th International Conference on 2000, 2000: 714-717.

[3] Matthys A D R, Gilbert J A, Puliparambil J T. Endoscopic inspection using a panoramic annular lens [C]//Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series. 1991: 736-742.

[4] 赵烈烽. 高分辨环带成像系统特性及应用研究[D]. 杭州: 浙江大学, 2008.

[5] 侯慧杰, 白剑, 杨国光. 全景环形透镜三维空间成像展开算法的研究[J]. 光学仪器, 2006, 27(6): 43-47.

[6] 朱方明, 杨国光, 姚炜勇, 等. 全景环形透镜环形象的线性化研究[J]. 光子学报, 2001, 30(5): 589-593.

[7] Chen T, Chung K L. An efficient randomized algorithm for detecting circles [J]. Computer Vision and Image Understanding, 2001, 83(2): 172-191.

[8] Xiang T, Gong S G. Video behavior profiling for anomaly detection [J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2008, 30(5): 893-908.

[9] 王道义, 黄大为, 邬敏贤, 等. 全景环形透镜原理与特点剖析[J]. 光学技术, 1998, (1): 11.

[10] 程钢, 熊志辉, 陈立栋, 等. 一种DSP折反射全景图像实时展开方法[J]. 计算机应用, 2008, 28(9): 2286-2287.

[11] Duran O, Althoefer K, Seneviratne L D. Automated sewer pipe inspection through image processing [C]// IEEE Robotics and Automation, 2002. Proceedings. ICRA'02. IEEE International Conference on, 2002: 2551-2556.

[12] 邓松杰, 周松斌, 程韬波. 利用鱼眼镜头生成全景图像的方法[J]. 图学学报, 2010, 31(1): 135-138.

[13] 罗年猛, 龚小寒, 朱林. 基于空间投影的管道施工图自动生成研究[J]. 图学学报, 2012, 33(4): 64-70.

Research of Adaptive Expansion Algorithm on Pipeline Inner-Surface Panoramic Image

Tang Aiping
(Creative & Art Design Department, Changzhou Textile Garment Institute, Changzhou Jiangsu 213164, China)

Panoramic annular lens is a special optical imaging device, which is used in morphology detection of pipeline. It is capable of ignoring hollow image in the radial direction and getting panoramic picture of whole pipeline inside wall. This has absorbed advantages of tangential expansion of traditional unwrapping algorithm, designing a calibration experiment, using edge extraction, Hough transform, and interpolation principle to improve radial development, and obtaining adaptive expansion algorithm to different pipe diameter. Simulation experiment showed that this method is effective to improve radial magnification, and applies to pipes with different diameters.

panoramic image; radial expansion; adaptive; simulation

TP 391

A

2095-302X(2015)06-0973-06

2015-09-21；定稿日期：2015-10-29

唐爱平(1979–)，男，江苏宿迁人，讲师，硕士。主要研究方向为多媒体图像技术。E-mail：tapjuan@163.com