基于四点偏置法的非可展直纹面侧铣刀位计算
严 涛, 刘志兵, 王西彬, 樊 勇
(北京理工大学机械与车辆学院,北京 100081)
基于四点偏置法的非可展直纹面侧铣刀位计算
严涛, 刘志兵, 王西彬, 樊勇
(北京理工大学机械与车辆学院,北京 100081)
针对非可展直纹面五轴侧铣加工的问题,分析了非可展直纹面几何特点,根据等距映射下的极差不变性,提出了一种计算非可展直纹面叶片五轴侧铣刀位数据的新方法。以刀具包络面与设计曲面之间的整体误差为优化目标,建立了圆柱铣刀侧铣非可展直纹面的刀位计算方法,运用四点偏置法确定初始刀位,采用最小二乘法对初始刀位进行优化,建立刀轴矢量偏转模型进一步修正刀位以减小过切误差。通过实例计算分析,表明该方法可以在一定程度上减小加工误差。
非可展直纹面;五轴侧铣;四点偏置法;刀位计算
非可展直纹面由直母线沿导线扫掠形成,是非可展的。以直纹抛物面为例,一条导线为直线,另一条导线为抛物线,直母线两端分别沿不同轨迹扫掠形成曲面。直母线上各点的法矢方向不同,将曲面离散,可以得到曲面上多条方向各不相同的直线。
整体叶轮叶片型面通常采用非可展直纹面,由于其曲面特性复杂,在数控加工中属于难度比较大的一类零件。为了满足精度需求,国内外学者大多从曲面的设计方法和加工方法两方面开展研究。Li等[1]提出最小二乘法、加权内部控制点法和无加权的内部控制点法三种侧铣曲面设计方法,分别对柱刀和锥刀进行了讨论。同时,对非可展直纹面加工方法的研究也一直是国内外学者关注的热点。Liu[2]提出了适用于柱刀侧铣的单点偏置法(single point offset,SPO)和双点偏置法(double point offset,DPO)。Redonnet等[3]提出了用于柱刀侧铣加工的三点规划方法,可以有效减小刀具表面与加工曲面的干涉,提高加工精度,但是该方法需要求解7个超越方程,计算比较复杂。Bedi等[4]提出一种圆柱刀加工直纹面的方法,刀具与两准线相切,接触点的参数值相等,最大过切发生在接近表面中间的部分。席光等[5]提出基于半径和角偏置的直纹面加工刀位生成算法,消除母线两端法矢异向引起的过切误差。Li等[6]提出空间切点位移法,在刀具与准线相切的同时增加沿母线方向的滑移,应用刀位规划三步优化法,减小了加工误差,这种算法计算精确度高,但计算非常复杂,不便于编程实现。Chu等[7]在刀位规划时考虑插值采样时间引起的加工误差,提出速度控制模型。朱利民等[8]提出一种针对圆锥刀侧铣加工的刀具路径优化方法,通过刀具包络面有向距离函数,构造出基于导数信息的刀具包络面到设计曲面的最佳一致逼近算法。Gong等[9]引入极差的概念,提出了三点偏置法来确定初始刀位,采用最小二乘法优化刀位。本文在三点偏置法及其改进算法的基础上,将整体优化方法和局部优化方法结合起来,运用四点偏置法计算初始刀位,并对所生成刀位进行刀轴矢量修正,进一步减小了过切误差。计算结果表明,本方法精度更高,具有较高的工程实用价值。
1 非可展直纹面侧铣加工理论基础
1.1刀位规划中的曲面分析
非可展直纹面的特点是直母线上各点的法矢方向不同,任何半径不为零的刀具对其进行侧铣都存在理论误差,刀具包络面不能与设计曲面完全相切,对于这种曲面的侧铣加工采用曲面逼近加工。考虑整体约束和局部约束,合理规划刀位轨迹,使误差范围尽可能小,是侧铣加工这类曲面的关键。
侧铣非可展直纹面叶片刀位规划主要涉及4类曲面:设计曲面、刀具包络面、设计曲面等距面、刀轴轨迹面。4类曲面对应关系如图1所示,其中柱刀的刀具包络面和刀轴轨迹面是一对等距面。
图1中,设计曲面是由整体叶轮叶片所形成的非可展直纹面;刀具包络面是侧铣加工时刀具侧刃在空间运动的扫掠轨迹面;刀轴轨迹面是侧铣加工中,刀具轴线扫掠形成的直纹轨迹面。刀轴轨迹面包含了刀具空间运动的全部信息,因此刀位规划实质上是构造出一个刀轴轨迹面,使刀具包络面尽可能逼近设计曲面,从而减小加工误差。
1.2几种侧铣加工刀位规划方法的误差对比
直纹面侧铣加工刀位规划方法包括两点偏置法、两点偏置优化法、三点偏置法、三点偏置优化法等,本文针对以上4种方法进行误差分析。图2为各算法误差对比。其中横坐标v代表点在直母线上的位置,范围为[0,1]。

图2 各算法误差分布
三点偏置优化法在三点偏置法的基础上进行了改进,两端点沿刀轴矢量进行了滑移,使误差范围进一步减小。但是该方法在v=0和v=1两端点处误差不为零,理论残留高度不为零,不适合分片侧铣的情况。三点偏置法相对于两点偏置法及两点偏置优化法在精度上有很大提高,三点偏置优化法在三点偏置法的基础上进行改进,加工误差进一步减小,但是端点处无限制,不适用于分片侧铣。本文在此基础上提出一种新的刀位计算方法。
2 柱刀侧铣加工的刀位计算方法
根据微分几何中等距映射下的极差不变性可知,刀具包络面和设计曲面的极差与刀轴轨迹面和设计曲面等距面之间的极差相等,因此可以将刀位的优化问题转变为如何尽可能减小刀轴轨迹面和设计曲面等距面的误差,即:①利用四点偏置法确定刀具的初始位姿;②以最小二乘法对初始刀位进行优化,进一步减小误差带范围;③对各刀位进行过切误差检测并对刀位进行最终修正。
2.1确定初始刀位的四点偏置法
直纹面定义为:

其等距面定义为:

其中,R为柱刀刀具半径;B0(u)和B1(u)为两条曲线的矢径;n(u,v)为曲面单位法矢。
四点偏置法确定初始刀位的步骤如下(如图 3所示):
步骤 2. 设定标准值 ε,并引入范围在[0,0.5]的λ,分别以v=λ和v=1–λ选定四点法中间两点的位置,分别用E1和E2表示两点与设计曲面等距面上对应点的距离。为了避免优化时刀轴偏转过大,各刀位P3点滑动范围设定为其中h为走刀步长与准线长度之比。
步骤3. 固定P0点,令P3点在内滑动,可以得到一族P0P3,分别计算每一步中当满足E < ε时,该直线即确定为初始刀位的刀轴方向。

图3 四点偏置法计算流程

图4 初始刀轴的确定
四点偏置法的实质是在设计曲面四条曲线上寻求四点,让其沿着曲面法矢偏移一个刀具半径R得到对应四点,使之精确逼近一条直线,其直线的方向即为刀轴方向。四点偏置法相对于三点偏置优化法精度更高,且两准线处误差为零,两次走刀理论残留高度为零,适用于分片侧铣。
将λ作为已知量带入模型进行初始刀位计算,然而实际加工时λ取何值时初始刀位误差最小是需要计算的。取0.1~0.4之间间隔为0.1的4个λ值,分别进行上述步骤确定初始刀位,对于每个λ生成的初始刀位进行 B样条拟合得到各初始刀轴轨迹面,计算各轨迹面与设计曲面等距面的误差范围,进行插值得出使误差范围最小的λ,即为所求。
2.2确定优化刀位的最小二乘法
由上述算法得到的刀轴矢量能保证在单刀位局部最优,利用蒙面法插值所得直纹面为初始刀轴轨迹面,还需要对其采用最小二乘法优化后才能使整体偏差最小,生成优化刀轴轨迹面。设刀轴轨迹面表示为:

其中,v为直母线方向参数;Ni,k(u)为 B样条基函数;bi和di为两准线控制顶点。
该曲面的控制点数为 2(n+1),对于等距面上M个数据点Ps(s=0,1,···,M–1),其在直纹面上对应点的参数为 a(us,vs),把 M 个点的数据带入式(3),得:

写成矩阵的形式为:

其中,


将X当作未知量,当M大于控制点数时,可以利用最小二乘法确定优化点。以数据点 Ps到轴迹面距离的平方和最小为目标,则目标函数为:
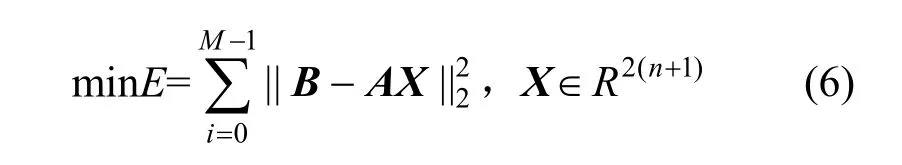
求解该方程组可得到优化后各控制顶点,即优化后的刀位信息,从而得到优化刀轴轨迹面。
2.3减小过切误差的刀位修正方法
从误差范围的角度已经对刀位进行了优化,而由于过切误差对于非可展直纹面叶片表面质量的影响远大于欠切误差,现从减小过切误差的角度对刀位进行再次修正。非可展直纹面型面复杂,要完全消除过切误差比较困难,可将两点偏置法误差曲线近似为抛物线,把三点偏置法看成两个两点偏置法的叠加,由三点偏置法及其优化方法的误差分布图可知,四点偏置法最大过切可能发生在直母线 λ/2,0.5,1–λ/2三点附近,利用二次搜索法确定最大过切点,对于每个刀位,对以上三点附近进行初步搜索,在过切误差最大的点附近进行二次搜索。对刀位进行修正的方法是固定刀心点,对刀轴矢量进行偏转,使最大过切误差满足要求。
对四点偏置法误差进行分析,误差分布如图5所示。

图5 四点偏置法误差分布
图5中Pd为设计曲面上的点;沿该点法向偏置一个刀具半径得到q0;Pt为特征线上一点;沿同一方向偏置后得到q;q和q0的距离ε即为该点的加工误差;v为直母线方向;u为准线方向。
针对四点偏置法的过切误差进行刀位修正,修正流程图如图6所示。

图6 减小过切误差的刀位修正流程
设最大过切误差为Emax,以P0为圆心沿最大误差点处的法向旋转刀轴,根据图7中模型计算出完全消除该点误差需旋转的角度 θ,由于刀轴偏转后各点误差也会产生变化,不能通过直接偏转θ来消除过切误差,以θ/n为增量进行迭代运算,n为刀位数,设定一个公差值εa,每次计算最大过切误差,直到即获得最终刀位。

图7 最大过切点处偏转模型
偏转角θ求解过程:如图7所示,旋转前刀轴为OM,旋转后为ʹM,夹角即为所求θ,三角形KMOʹ相似于KPdO,OPd= r–Emax。

3 计算实例
根据前面提出的算法,采用直径为10 mm的柱刀对曲面进行加工,设计曲面参数如下:
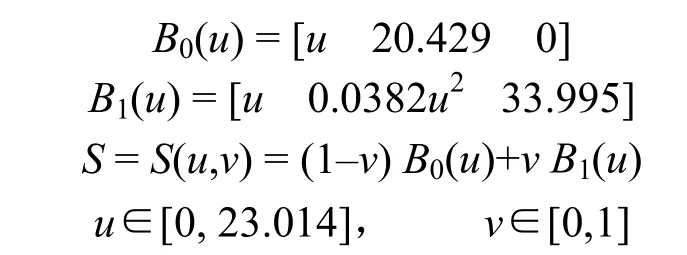
设计曲面与加工过程中刀具姿态如图8所示。

图8 曲面与刀具姿态
用 4种刀位计算方法对设计曲面进行仿真加工,比较各方法加工误差,如表1和图9所示。

表1 各方法加工误差对比(mm)

图9 各方法加工误差对比图
4 结 论
本文针对非可展直纹面五轴侧铣加工的刀位路径规划,提出了四点偏置法确定初始刀位,利用刀位修正模型减小过切误差;通过引入比例因子λ,建立了柱形球头铣刀五轴数控侧铣加工非可展直纹曲面的刀位算法,建立了非可展直纹面叶片五轴侧铣刀轨优化的理论方法。计算结果验证了本文所提出的五轴侧铣加工直纹面整体叶轮方法的正确性和实用性。
[1] Li C G, Bedi S, Mann S. Flank millable surface design with conical and barrel tools [J]. Computer-Aided Design & Applications, 2008, 5(1/4): 461-470.
[2] Liu X W. Five-axis NC cylindrical milling of sculptured surfaces [J]. Computer-Aided Design, 1995, 27(12): 887-894.
[3] Redonnet J M, Rubio W, Dessein G. Side milling of ruled surfaces: optimum positioning of the milling cutter and calculation of interference [J]. The International Journal of Advanced Manufacturing Technology, 1998, 14(7): 459-465.
[4] Bedi S, Mann S, Menzel C. Flank milling with flat end milling cutters [J]. Computer-Aided Design, 2003, 35(3): 293-300.
[5] 席光, 吴广宽, 郑健生. 基于半径和角偏置的直纹面五坐标加工刀位生成算法[J]. 机械工程学报, 2008, 44(4): 92-96.
[6] Li C G, Bedi S, Mann S. Flank milling of ruled surface with conical tools-an optimization approach [J]. The International Journal of Advanced Manufacturing Technology, 2006, 29(11-12): 1115-1124.
[7] Chu C H, Huang W N, Hsu Y Y. Machining accuracy improvement in five-axis flank milling of ruled surfaces [J]. International Journal of Machine Tools & Manufacture, 2008, 48: 914-921.
[8] 朱利民, 郑刚, 丁汉. 圆锥刀五轴侧铣加工刀具路径整体优化原理与方法[J]. 机械工程学报, 2010, 46(23): 174-179.
[9] Gong H, Cao L X, Liu J. Improved positioning of cylindrical cutter for flank milling ruled surfaces [J]. Computer-Aided Design, 2005, 37: 1205-1213.
Cutter Location Calculation Based on the Four Offset Method of Flank Milling for Undevelopable Ruled Surface
Yan Tao,Liu Zhibing,Wang Xibin,Fan Yong
(School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China)
The existing method of five-axis flank milling to machine undevelopable ruled surface is researched, through the analysis of the geometric characteristics of the undevelopable ruled surface, a new method is proposed to calculate the cutter location data of five-axis flank milling with undevelopable ruled surface impeller. The global error optimization between the tool envelope surface and the design surfaces is the goal, and a method to calculate the cylindrical cutter location when flank milling the undevelopable ruled surface is established, putting forward a four-point method to determine the initial cutter location, optimizing it using the least squares method, establishing cutter correction model to further optimize the cutter location to reduce the over-cut error. By analyzing the example, it is proved that processing error can be reduced to some extent through this method.
undevelopable ruled surface; 5-axis flank milling; offset method of four points; cutter location calculation
TH 161+.1
A
2095-302X(2015)06-0840-06
2015-05-18;定稿日期:2015-07-21
国家自然科学基金资助项目(51375055)
严涛(1990–),男,湖北宜昌人,硕士研究生。主要研究方向为数控加工。E-mail:yantao224@163.com
刘志兵(1977–),男,河北藁城人,副教授,博士。主要研究方向为精密微细切削技术。E-mail:liuzhibing@bit.edu.cn

