基于MLPG法的船舶结构无网格自适应分析技术

陈建平，唐文勇，徐曼平

(1.上海交通大学 船舶海洋与建筑工程学院，上海200240;2.广州航海学院 船舶工程学院，广东 广州510725)

0 引 言

当前船舶结构分析最常用也最为有效的计算工具之一就是有限元方法，有限元方法在分析、处理和模拟船舶结构变形、应力和疲劳分析等都有着广泛和成熟的应用［1］。但有限元法因其自身的特点，在处理分析船舶结构场量(位移场和应力场等)变化剧烈的高梯度区域时，会出现计算精度降低甚至计算中断现象。为了解决这个问题，有限元法通常采用对该区域的网格进行加密(细分)或者采用高阶单元，这样就要求方法具有较强的自适应分析能力，其结果是加大了有限元法前后处理的工作量，从而降低了计算效率，事实上这种方法也并不能从根本上消除问题产生的根源。

作为与有限元法相对应的另一种数值分析方法——无网格法，在近20年中得到了很大发展［2-6］。无网格法是建立在系列独立离散点的基础上，通过构造点的近似函数来求解问题。与传统有限元法相比，无网格法无需网格背景，在计算过程中可以根据需要任意增减节点，而不需要处理节点之间的拓扑信息，特别适合用来进行自适应分析计算。另外由于无网格法没有必要创建网格，节点可以由计算机以自主方式进行创建，可以节省花费在创建和处理网格的时间和计算资源。无网格法目前在航空材料、高速碰撞、动态裂纹扩展、加工成型、节理岩体分析等诸多领域都得到了较为广泛的应用［7-10］。

本文鉴于上述现状和背景，提出基于局部无网格Petrov-Galerkin法的船舶板结构无网格自适应分析技术。首先将需要分析的船舶板结构简化为平面板结构，并将此结构定义为问题域;再根据二维弹性理论，采用在离散节点上建立紧支试函数，运用加权余量法建立系统的离散方程;然后由移动最小二乘法(MLS)构造离散节点的形函数，通过离散积分方程的等效弱形式来进行求解。运用Delaunay 三角化细分方案来执行节点加密自适应计算方案。本文的本质边界条件采用全转化法的方法来处理。最后选取了2 种典型船舶结构进行应力分析计算，并与有限元法的计算结果进行比较来验证本文方法的有效性。

1 船舶结构MLPG法表达式

由于船体板的板厚远小于其另外2个方向(长度和宽度)的几何尺寸，在分析其受力时，可以运用Kirchhoff-Love板壳理论和Mindlin-Reissner板壳理论。本文基于板壳的Mindlin-Reissner的基本理论，运用局部无网格Petrov-Galerkin法(MLPG)，来分析研究无网格法下的船舶板结构应力。

1.1 节点控制方程

板结构经离散后二维弹性理论为基础的节点系统方程［11］

式中:i和j 为板的2个维度;σij，i为应力σij在i 方向的分量;bi为板在i 方向的体积力;Ω 为问题域;Γ 为Ω的边界;ui=;Γu为问题的本质边界条件;σijnj=;Γt为问题的自然边界条件;nj为自然边界上单位外法向矢量的第j个分量。

利用加权余量法［12］，可以得到节点I 处系统方程的微分方程强形式为

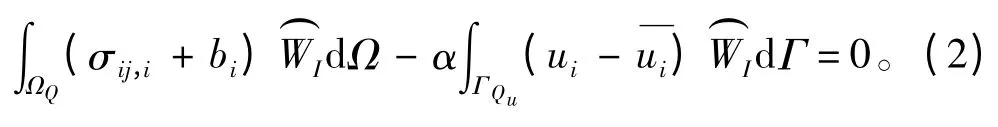
对节点I 依式(2)在其积分域上进行积分，可以建立起它的系统方程。这样对每个节点都采用式(2)在其积分域上积分，可以得到所有离散节点的系统方程，将这些离散节点的系统方程组装起来就能够获得问题域的整体系统方程。

利用移动最小二乘法(MLS)得到节点的积分点支撑域内的形函数，从而获得问题域的位移逼近函数［12］。

式中:ΦT(X)为根据MLS所得的形函数矩阵;uI为离散节点I的节点值;N 为积分点的支撑域Ωs中的节点数。

根据弹性力学应力-应变关系有

国内外已有使用激光进行高速目标测速的相关研究，常用方法大致可分为三类：一是基于直接光谱技术，利用法布里-珀罗干涉仪直接测量谱线的频移[5]；二是双激光拍频技术，利用两个线偏振光同时传感物体的速度，可大大提高最高可测量速度[5-10]；三是利用外调制技术，使用微波作为模拟调制信号对激光进行强度调制，通过检测微波调制信号的多普勒频率，来实现相对运动速度的测量[11-13]。相比于双激光拍频技术，采用外调制技术降低了对激光器线宽和稳定度的要求，更容易实现高精度和高动态的测量。2016年，郝文泽等人采取强度调制和直接探测的方式，成功获得了可靠的测速实验数据[13]。

式中:D 为材料弹性矩阵;B 为几何矩阵，且Bj=

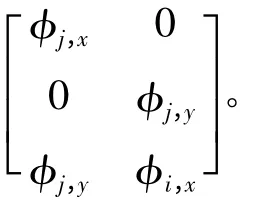
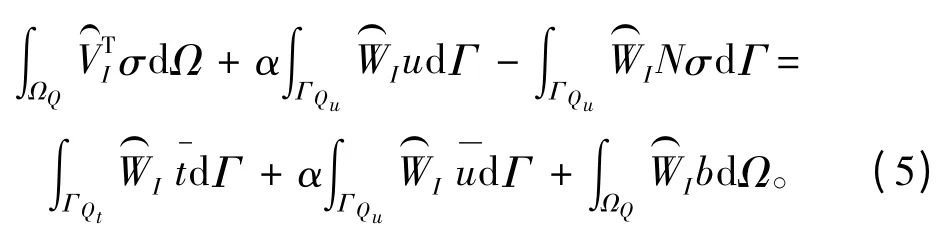
式中:ΓQt为积分域ΩQ和自然边界的重合部分;N为自然边界上的单位外法向矢量矩阵。

1.2 刚度方程

把节点系统方程式(3)和式(4)代入节点控制方程式(5)，可以得到

式(6)可简记为矩阵形式

其中

这样，由每个离散节点的控制方程总装成整个结构系统的控制方程表达为

由于在MLS 中，采用的节点支撑域都是紧支的，系统的总体刚度矩阵K 是带状稀疏矩阵，可以减少计算负荷。根据文献［13］对有限元法中罚因子的分析，建议罚因子α 在范围内105～12× E 取值，E为杨氏弹性模量。

2 自适应细分计算

图1 细分方案示意图Fig.1 Refinement scheme by local Delaunay algorithm

算法流程为:

1)影响域三角化:在确定不符合精度要求的节点i 后，在其影响域内搜索相邻节点并利用这些节点进行三角化;

2)插入新节点:遍历环绕节点i的所有三角形，在三角形各条边的中点上加入新的节点;

3)删除冗余节点:删除重复节点，使得每个位置只有1个节点。若任意2个节点允许的最小距离为dm，判断两新节点间距离小于dm，则需删除其中一个节点。

4)删除三角形:在局部区域内删除三角形的边。

自适应计算误差确定采用如下的相对误差估计方法［14］:

当相对误差值小于给定的计算误差值，该节点计算自动终止，转入下一节点的计算，并执行下一节点的自适应计算方案。

3 本质边界条件施加

因无网格法形函数ΦT(X)不满足克罗内克条件，对于刚度方程式(7)中的节点I的参数u 并非其真实位移，所以本质边界条件不能够像有限元法那样直接施加。Chen J S 等提出了全转换法(Full transformationmethod)［15］来处理其边界条件。本文按照全转换法的原理对刚度方程(控制方程)进行修正得到

4 算 例

为了验证文章方法的正确性，本节给出船舶结构中“实肋板”和“裂纹板”2 种典型结构的分析计算。本文算例中材料的杨氏弹性模量为E=2.1 ×105MPa，泊松比μ=0.3。

4.1 实肋板

中间开有减轻孔的实肋板结构是船舶普通结构之一。图2 简化为上下两端自由、另两端承受均匀拉力的船体实肋板。板侧均布拉力q=1 MPa。

图2 典型实肋板示意图Fig.2 The typical solid floor

根据本文算法，采用不规则初始离散节点245个。经过6 步自适应计算，每个自适应步离散图和计算出的应力云图如图3所示。

各自适应步在实肋板沿Y 方向对称轴上的应力比较(考虑X 方向也对称，只取一半比较)如图4所示。从图中可看出，曲线变化趋势存在局部反弹，但总体趋势是在收敛，且收敛方向趋于一致。

图3 自适应离散图和应力云图Fig.3 The discrezition figure and fringe firgure

图4 Y 各自适应步方向轴线上应力变化图Fig.4 The curve of Mises stress along Y-Direction inmidsection

图5 为本文方法计算结果与有限元软件Ansys和Nastran 以及用解析法计算的结果比较图。从图示各图线来看，本文方法比在靠近板边缘和孔的边缘附近处，比有限元法有着更好的精度。

图5 各种方法计算应力结果比较图Fig.5 The curve of Mises stress with different ways

各自适应步在实肋板沿Y 方向对称轴上的应力相对误差比较(考虑X 方向也对称，只取一半比较)如图6所示。由图中可看出，相对误差虽然存在局部震荡情况，但每一步变化趋势都是在减小，说明计算精度在逐步提高，说明文章方法具有很好的计算精度。

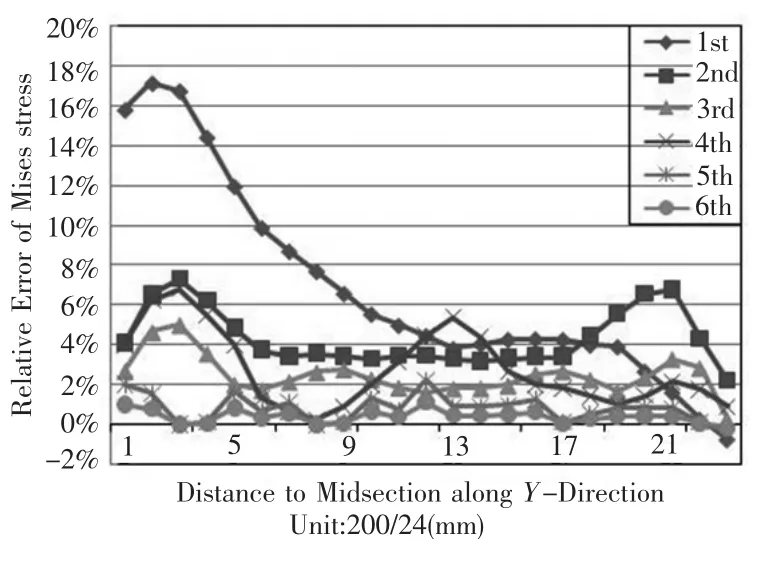
图6 相对误差变化图Fig.6 The curve of the relative error

4.2 裂纹板

一长边为1 m，短边为0.5 m，在长边中部边缘沿Y 方向有一裂纹长为100 mm。板上下两端为自由边，侧边受均布拉力p=10 N/m。

根据本文算法，采用不规则初始离散节点137个。经过5 步自适应计算，每个自适应步离散图和计算出的应力云图如图7所示。

图7 自适应离散图和应力云图Fig.7 The discrezition figure and fringe firgure

各自适应步从边缘到裂纹尖端沿Y 方向的应力比较如图8所示。从图中可看出，曲线在两端变化较大，但总体趋势是在收敛，且收敛方向趋于一致。

各自适应步沿裂纹方向的应力相对误差比较如图9所示。由图可知，相对误差虽然存在局部震荡情况，但每一步变化趋势都在减小，说明计算精度在逐步提高，说明本方法具有良好的计算精度。

图8 沿裂纹方向应力变化曲线Fig.8 The curve of the Mises stress along the crack line

图9 相对误差变化图Fig.9 The curve of the relative error

5 结 语

本文基于无网格局部MLPG法，提出了船舶结构的无网格分析方法，并采用Delaunay 三角化方法对节点进行自动加密计算。最后运用所提方法对典型的船舶结构——船体实肋板和裂纹板的分析计算，并通过与有限元法的计算结果进行比较，可以看出本文提出的无网格自适应分析方法对于求解船舶结构的变形(位移)和应力可行，并且具有良好的精度，验证了本文方法的有效性和准确性。

［1］孙丽萍，李力波.船舶结构有限元分析［M］.哈尔滨:哈尔滨工程大学出版社，2013.

［2］BELYTSCHKO T，KRONGAUZ Y，ORGAN D，et al.Meshless methods:An overview and recent developments［J］.Computer Methods in Applied Mechanics and Engineering，1996，139:3-47.

［3］LIU W K，HAO S，BELYTSCHKO T，et al.Multiple scale meshless methods for damage fracture and localization［J］.Comput.Mater.Sci.，1999，16:197-206.

［4］ATLURI S N，SHEN S.The basis of meshless domain discretization: the meshless local Petrov- Galerkin(MLPG) method ［J］.Advances in Computational Mathematics，2005，23:73-93.

［5］ODEN J T，DUARTE C A，ZIENKIEWICZ O C.A new could-based hp finite element method［J］.Int.J.Num.Meth.Engng.，1998，50:160-170.

［6］LIU G R，GU Y T.Meshless local Petrov-Galerkinmethod in combination with finite element and boundary element approaches［J］.Computational Mechanics，2000，26:536-646.

［7］何沛祥，李子然，吴长春.无网格与有限元的耦合在动态断裂研究中的应用［J］.应用力学学报，2006，23(2):195-198.HE Pei-xiang，LI Zi-ran，WU Chang-chun.Coupled finite element-element-free galerkinmethod for dynamic fracture［J］.Chinese Journal of Applied Mechanics，2006，23(2):195-198.

［8］段念，王文珊，于怡青，等.基于FEM 与SPH 耦合算法的单颗磨粒切削玻璃的动态过程仿真［J］.中国机械工程，2013，24(20):2716-2721.DUAN Nian，WANG Wen-shan，YU Yi-qing，et al.Dynamic simulation of single grain cutting of glass by coupling FEM and SPH ［J］.Chinese Mechanical Engineering，2013，24(20):2716-2721.

［9］JOHNSON R G，STRYK A R，BEISSEL R S，et al.An algorithm to automatically convert distorted finite element into meshless particles during dynamic deformation［J］.International Journal of Impact Engineering，2002，27:997-1013.

［10］胡德安，韩旭，肖毅华，等.光滑粒子法及其与有限元耦合算法的研究进展［J］.力学学报，2013，45(5):639-652.HU De-an，HAN Xu，XIAO Yi-hua，et al.Research developments of smoothed particle hydrodynamics method and its coupling with finite element method［J］.Chinese Journal of Theoretical and Applied Mechanics，2013，45(5):39-652.

［11］LIU G R.Meshfree methods moving beyond the finite element method［M］.CRC Press，2003.

［12］ATLURI S N，ZHU T.A new meshless local Petrov-Galerkin(MLPG)approach in computational mechanics［J］.Computational Mechanics，1998，22:117-179.

［13］ZIENKIEWICZ O C.The finite element method［C］//4th ed.，McGraw-Hill，London，1989.

［14］GAVETE L，FALCON S，RUIZ A.An error indicator for the element free Galerkinmethod ［J］.European Journal Mechanics-A/Solids，2001，20(3):327-341.

［15］周培德.计算几何［M］.北京:清华大学出版社，2000.