带形状参数曲线的最优参数取值问题研究

刘成志， 李军成， 杨 炼

(湖南人文科技学院数学系，湖南 娄底 417000)

带形状参数曲线的最优参数取值问题研究

刘成志， 李军成， 杨 炼

(湖南人文科技学院数学系，湖南 娄底 417000)

带形状参数的曲线中所带形状参数的取值通常是一个区间，但在实际问题中往往需要确定形状参数的最优取值，以使得曲线具有良好的光顺性。针对这一问题，首先基于曲线的光顺准则建立了一个求解带形状参数曲线最优参数取值的通用数学模型，然后给出了利用遗传算法求解该模型的具体步骤，最后以两类带形状参数的曲线为例验证了所提出方法的有效性。

参数曲线；形状参数；最优参数值；光顺；遗传算法

在曲线曲面造型中，由于带形状参数的曲线曲面不仅具有相应传统曲线的主要性质，而且还可以通过修改形状参数的取值来调整其形状，因此带形状参数的曲线曲面造型方法已成为研究的热点之一。目前，国内外学者提出了许多不同的带形状参数曲线曲面的构造方法，大致可分为3类：①带形状参数的多项式曲线曲面，即在传统的多项式曲线曲面中引入形状参数构造出带形状参数的多项式曲线曲面[1-5]；②带形状参数的非多项式曲线曲面，即通过改变传统多项式曲线曲面的基函数，在非多项式函数空间中构造带形状参数的曲线曲面[6-10]；③带形状参数的奇异混合曲线曲面，即通过借助奇异混合技术，将参数曲线曲面与奇异混合函数相混合，构造出带局部形状参数的插值曲线曲面[11-14]。

目前，关于带形状参数的曲线曲面造型方法已取得较为丰硕的研究成果，但值得注意的是，带形状参数的取值通常是一个区间。在实际问题中，为了使得曲线具有良好的光顺性，往往需要确定形状参数的最优取值。虽然文献[15]利用遗传算法对最优形状参数的取值进行了研究，但仅局

限于三次 β样条曲线的最优形状参数的确定，可移植性不高。

本文基于曲线的光顺准则建立了求解曲线形状参数最优取值问题的通用数学模型，该模型能够求解任何带形状参数曲线的近似最优形状参数，具有良好的可移植性。并给出了利用遗传算法求解该模型的过程，最后以两类带形状参数的曲线为例，求解出各自近似最优的形状参数，验证所求的最优形状参数能够保证曲线具有较好的光顺性。

1 参数曲线最优形状参数模型的建立与求解

1.1 参数曲线最优形状参数模型的建立

带形状参数曲线所带的形状参数通常是在一个区间内取值，而在实际问题中，往往需要确定形状参数的最优取值，以使得曲线具有良好的光顺性。

根据光顺准则，曲线曲面的能量在很大程度上反映了曲线曲面的光顺程度。当曲线的能量值最小时可得到最光顺的曲线。因此参数曲线最优形状参数的取值可以归结为优化问题，考虑利用能量优化法求解形状参数的最佳取值。首先给出曲线的能量定义，设某带形状参数的参数曲线为r(t)(a≤t≤b)，其中r(t)中含有形状参数λi且λi∈I(i=1,2,…,n)。

曲线 r(t)的能量函数[16]可表示为：

为了保证曲线具有良好的光顺性，需曲线的能量 E值最小。因此以曲线的能量函数作为目标函数，参数作为决策变量，形状参数的取值范围作为约束条件建立最优化模型如式(1)：

1.2 求解参数曲线最优形状参数模型的求解

对式(1)的求解有很多方法，如牛顿法、共轭法等传统优化算法以及遗传算法、蚁群算法等智能算法。由于目标函数较为复杂且需要求导和求积运算，用传统优化算法求解较为困难且容易得到局部极小，遗传算法能够很快地通过迭代寻找近似全局最优解，因此本文利用遗传算法求解最佳形状参数，首先给出遗传算法的基本原理。

1.2.1 遗传算法的基本原理

遗传算法[17]是借鉴进化生物学中的进化现象而发展起来的优化算法。遗传算法通过编码、选择、交叉和变异来实现。

(1) 编码方案：采用二进制编码来离散决策变量(形状参数)，即将决策变量在区间上的连续取值离散转换成二进制的代码，形成染色体基因。码长根据离散的精度来确定，设参数λ的变化区间为[a,b]，取决策变量的离散精度为ε。设码长为L，根据算术编码方案，取其中表示向上取整运算。任何一个长度为 L的码字均对应于形状参数在[a,b]上的某个取值。

(2) 基因选择：在进化过程中，父代个体以一定概率被选择去繁殖下一代。通常适应度高的个体更容易被选择，适应度函数的构造方法有轮盘赌选择方法[8]、锦标赛选择方法[8]等。虽然适应度函数已经有很多构造方法，但它的选择对遗传算法的计算结果影响非常大。为了简化，本文选取个体在能量函数中的函数值作为适应度函数，能量值低的个体适应度高。选择能量函数值作为适应度函数不仅符合适应度函数的选取规则，还能减少迭代过程中的计算量，更重要的是在求解任意带形状参数的最优形状参数时，不需修改适应度函数。

(3) 基因交叉：采用单点交叉。 假设在父代种群中有以下两个个体：

以一定的交叉概率 Pc确定交叉点，在上例中不妨为下划线的码字。则通过交叉之后变为：

(4) 基因变异：对个体而言，基因变异是以一定的变异概率 P 改变染色体中的基因值。设个体：

若该染色体基因的第二位产生变异，则通过变异之后个体的染色体基因变为：

1.2.2 求解最优形状参数的遗传算法

对于最优化模型式(1)，采用遗传算法求解，流程如下：

(1) 初始化。输入遗传算法的种群规模NP，杂交概率 Pc，变异概率 Pm，自变量离散精度ε，最大

进化次数N；

(2) 随机产生规模为 NP的初始种群，同时对种群中的每个个体进行二进制编码，如果有多个形状参数，每个形状参数均可视为种群中的某个个体，即分别进行；

(3) 计算种群 NP中各个体的适应度，以曲线的函数值作为适应度函数。并判断个体是否符合优化准则，即能量值低的个体适应度高。若符合优化准则，则输出，否则进行下一步；

(4) 根据杂交概率Pc对种群进行交叉操作，产生新个体；

根据变异概率 Pm对种群进行变异操作，产生新个体，转入(3)。若算法的进化次数超过N，则停止迭代。

2 求解两类带形状参数曲线最优参数取值实例

2.1 两类带形状参数的参数曲线简介

定义 1[1]. 给定 R2或 R3空间中 3个控制顶点Vi(i = 0,1,2)，则曲线：

为可调控的三次参数曲线，其中：

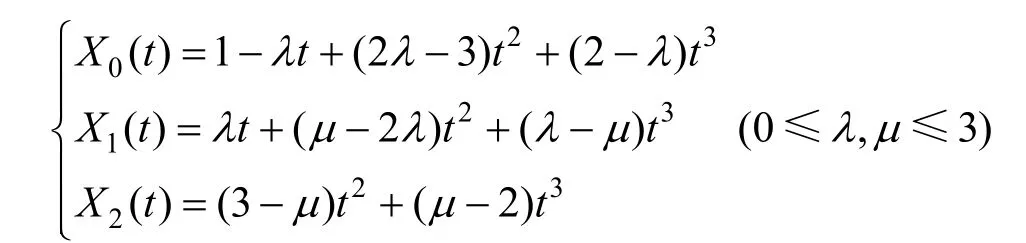
由文献[1]可知，式(2)定义的可调控的三次参数曲线是二次 Bézier曲线的扩展，其具有许多与二次 Bézier曲线相似的性质，如端点性质、拟对称性、凸包性和几何不变性等。更重要的是，该曲线可以通过修改参数值而不是改变控制顶点来调整曲线的形状，当控制顶点不变，形状参数λ与μ分别取不同值时，可得到一组形状不同的曲线，如图1所示。

图1 形状参数取不同值时的三次参数曲线

此外，在设计复杂的自由曲线时，常常会遇到曲线段之间的拼接。设 r1(t)与 r2(t)分别为两条可调控三次参数曲线，其中形状参数为0≤ λ1,μ1≤ 3，r1(t)的控制顶点为 P0,P1,P2；r2(t)的控制顶点为 Q0,Q1,Q2。当P1，P2=Q0，Q1三点共线时，可调控的三次参数曲线段 r1(t)与 r2(t)之间满足 G1拼接[1]。

定义2[10]. 给定4个控制顶点 b0,b1,b2,b3，则曲线：

为带有形状控制参数的三次代数三角插值样条，简称CATI-样条曲线，其中：

由文献[10]可知，CATI-样条曲线除了具有端点性、对称性、保凸性、几何不变性等性质之外还有形状可调性，即给定4个控制顶点时，可通过改变参数λ的取值调整曲线的形状，如图2所示。

2.2 求解带形状参数曲线的最优形状参数

2.2.1 求解可调控的三次参数曲线最优形状参数

例如，给定控制顶点V0=(0,1)，V1=(1,2)，V2=(2,1)， V3=(3,0)， V4=(4,1)，V5=(5,2)，V6=(6,1)。根据定义1，分别由控制顶点 V0V1V2、V2V3V4、 V4V5V6定义 3条可调控的三次参数曲线ri(t)(i = 1,2,3)。取种群规模NP=300， Pc=0.9，Pm= 0.04， N= 100， ε= 0.005。利用遗传算法分别求出3条参数曲线在各控制多边形下参数曲线的最优能量值，如表1所示。

图2 形状参数取不同值时的CATI-样条曲线

表1 可调控的三次参数曲线最优形状参数及对应能量值

为了验证遗传算法所求结果为最优形状参数，同时给出由控制顶点 V0V1V2定义的r1(t)在形状参数取不同值时的能量值，如表2所示。

由表1和表2可知，当 λ= 1.5015，μ =1.497 7时参数曲线的能量值与λ， μ 取其他参数时曲线的能量值相比为最低，因此从曲线的能量值角度看，结果符合能量优化准则。

形状参数取最优值及其他值时的曲线如图 3所示，需要说明的是，由于V1V2V3，V3V4V5分别三点共线，故曲线段 r1(t)、r2(t)、r3(t)之间满足G1连续。

表2 r1 (t)在形状参数取不同值时的能量值

图3 形状参数λ,μ取不同值时的三次参数曲线

2.2.2 求解CATI-样条曲线最优形状参数

例如，设有 6 个控制顶点 b0= (0,0)，根据定义 2分别由控制顶点 b0b1b2b3、b1b2b3b4、b2b3b4b5定义3条带有形状控制参数的三次代数三角插值样条曲线 ri(t)(i = 1,2,3)，其形状参数分别为-0.5 ≤λ≤ 0.5。

根据遗传算法，取种群规模NP=300， Pc=0.9，Pm= 0.04， N= 100， ε= 0.005。分别求出3条参数曲线在各控制多边形下参数曲线的最优能量值，同时将最优形状参数与其他参数取值的能量值进行比较，如表3所示。

形状参数取最优值及其他值时的曲线如图4所示，需要指出的是，在第二段样条曲线中，最优参数曲线与 λ= 0.5时的参数曲线近似重合，这是因为

此时最优参数为0.498 7与0.5相近，且曲线的能量值也极为相近。同时，通过比较表1和表2可见，当 λ= 0.5时第 2段参数曲线的能量值比遗传算法求得的曲线能量值还要低，但相差不大，这是遗传算法的特点，因此该结果较为合理，可以作为优化问题近似最优解。

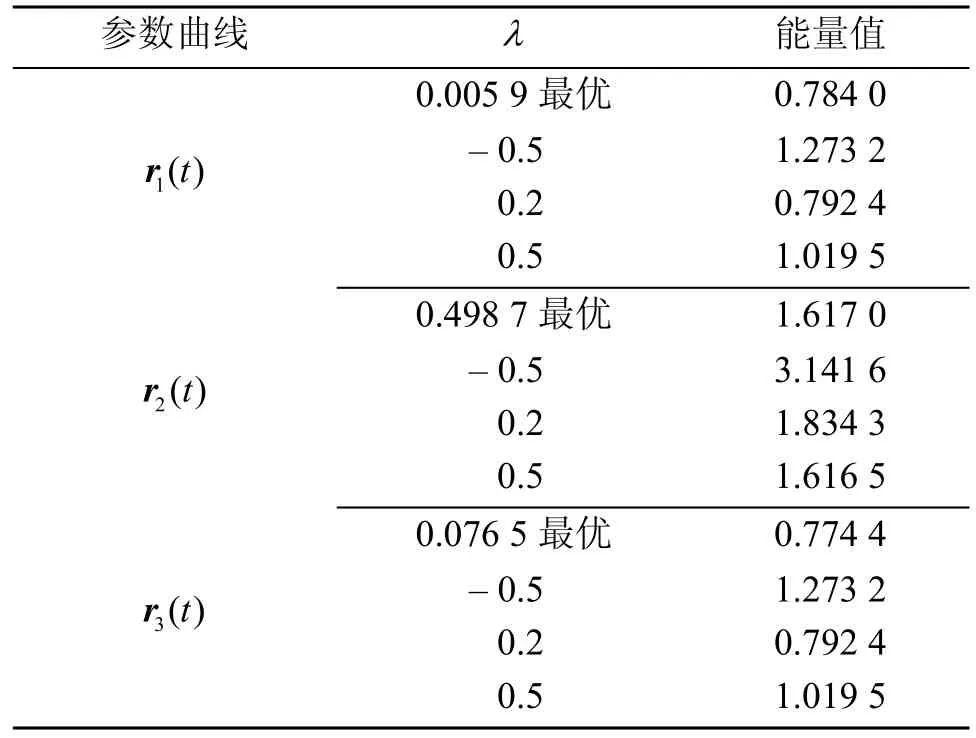
表3 CATI-样条曲线不同形状参数及能量值

图4 λ取不同值时的CATI-样条曲线

3 结 束 语

本文基于光顺准则建立了求解带形状参数曲线最优参数取值的通用数学模型，并给出了利用遗传算法求解该模型的具体步骤。最后以两类带形状参数曲线为例验证了该模型及求解算法的有效性。利用遗传算法求解带形状参数曲线的最优参数取值问题具有可移植性，对于不同的带形状参数的曲线，均可利用本文所提出的方法求解形状参数的最优取值。

[1] 李军成. 一类可调控的三次多项式曲线[J]. 计算机工程与科学, 2010, 32(4)： 52-54.

[2] Yan Lanlan, Liang Jiongfen. An extension of the Bézier model [J]. Applied Mathematics and Computation, 2011, 218(6)： 2863-2879.

[3] Chen Jie, Wang Guojin. A new type of the generalized Bézier curves [J]. Applied Mathematics-A Journal of Chinese Universities, 2011, 26(1)： 47-56.

[4] Fan Feilong, Zeng Xiaoming. S-λ bases and S-λ curves [J]. Computer-Aided Design, 2012, 44(11)： 1049-1055.

[5] Zhu Yuanpeng, Han Xuli. A class of αβγ-Bernstein-Bézier basis functions over triangular domain [J]. Applied Mathematics and Computation, 2013, 220(17)： 446-454.

[6] Han Xuli, Zhu Yuanpeng. Curve construction based on five trigonometric blending functions [J]. BIT Numerical Mathematics, 2012, 52(4)： 953-979.

[7] Juhász I, Róth Á. Closed rational trigonometric curves and surfaces [J]. Journal of Computational and Applied Mathematics, 2010, 234(8)： 2390-2404.

[8] Bashir U, Abbsa M, Ali J M. The G2 and C2 rational quadratic trigonometric Bézier curve with two shape parameters with applications [J]. Applied Mathematics and Computation, 2013, 219(20)： 10183-10197.

[9] 严兰兰, 梁炯丰, 黄 涛. 两种带形状参数的三角曲线[J]. 图学学报, 2012, 33(1)： 25-30.

[10] 杨 炼, 李军成, 匡小兰. 一类局部可调的三次代数三角插值样条[J]. 计算机工程与科学, 2013, 35(5)：130-135.

[11] Xu Gang, Wang Guozhao. Extended cubic uniform B-spline and α-B-spline [J]. Acta Automatica Sinica, 2008, 34(8)： 980-984.

[12] Hoffmann M, Juhásza I. On interpolation by spline curves with shape parameters [C]//Advances in Geometric Modeling and Processing. Berlin Heidelberg, Springer, 2008： 205-214.

[13] 张 莉, 刘静静, 檀结庆. 多形状参数的指数均匀B样条曲线曲面[J]. 图学学报, 2013, 34(3)： 29-35.

[14] Zhu Yuanpeng, Han Xuli, Han Jing. Quartic trigonometric Bézier curves and shape preserving interpolation curves [J]. Journal of Computational Information Systems, 2012, 8(2)： 905-914.

[15] 李彦红, 穆国旺, 郭 增. 用遗传算法确定三次β样条曲线的形状参数[J]. 计算机工程与应用, 2011, 47(9)：175-180.

[16] 朱心雄. 自由曲线曲面造型技术[M]. 北京： 科学出版社, 2000： 273-275.

[17] 龚 纯, 王正林. 精通MATLAB最优化计算[M]. 2版.北京： 电子工业出版社, 2011： 313-317.

Optimal Parameter Values of the Curves with Shape Parameters

Liu Chengzhi, Li Juncheng, Yang Lian
(Department of Mathematics, Hunan Institute of Humanities, Science and Technology, Loudi Hunan 417000, China)

Although the curve with shape parameters has become one of the most popular topics in the curve modeling, but the values of shape parameters are always given as intervals, while in practice, the optimal parameter values is often needed to ensure that the curves have good fairness and smoothness. According to this problem, firstly, a automatic mathematical model which is based on the fairing criterion is established to obtain the optimal parameters, and then the concrete steps of genetic algorithm is given to solve the model. At the last, two classes of curves are used as examples to illustrate the effectiveness of our methods.

parameter curve; shape parameter; optimal value of parameter; fairness and smoothness; genetic algorithm

TP 391.72

A

2095-302X(2015)04-0532-05

2015-01-16；定稿日期：2015-03-04

湖南省教育厅科研资助项目(14B099)；湖南人文科技学院校级青年基金资助项目(2013QN07)

刘成志(1986–)，男，湖南洞口人，硕士研究生。主要研究方向为数值代数。E-mail：it-rocket@163.com