改进EMD-小波分析的转子振动信号去噪方法

李 琳，张永祥，刘树勇

（海军工程大学 动力工程学院，武汉 430033）

改进EMD-小波分析的转子振动信号去噪方法

李 琳，张永祥，刘树勇

（海军工程大学 动力工程学院，武汉 430033）

针对低信噪比转子振动信号的去噪问题，提出了EMD和小波分析相结合的去噪方法。首先对含噪信号进行EMD处理，利用连续均方误差准则对IMF分量进行高低频区分。然后设定不同的阈值，利用小波分析对高低频IMF分量进行有用信号的提取，将提取的信号和低频IMF分量叠加重构，实现降噪。为了验证所提方法的有效性，进行了数字仿真和转子振动信号降噪分析，结果表明，所提方法整体上优于EMD和小波阈值去噪方法。

振动与波；混沌信号；EMD；小波分析；连续均方误差

旋转机械转子通常存在不对中、不平衡以及油膜涡动等故障，在信号采集过程中，由于测试仪器、环境及人为因素的影响，得到的振动信号易受到噪声的干扰，严重影响了转子系统故障特征提取。目前，国内外一些学者针对转子振动信号去噪方法做了大量研究工作[1-3]，其中小波分析具有良好的时频局部分析性能，在轴承信号的去噪中得到了广泛的研究与应用，小波阈值去噪法便是其中一种常用、简洁、有效的去噪方法。但是旋转机械转子工作环境复杂，相比于噪声，有效信号的幅值很小，被噪声“湮没”，此时采用小波分析去噪效果并不理想[4]。经验模态分解（Empirical Mode Decomposition，EMD）是一种新的处理非线性非平稳信号的方法，与小波分析相比，EMD是一种后验的处理方法，不需要事先选择基函数，且各IMF分量重构时没有能量损失，但是，Boudraa等[5]对EMD消噪算法和小波阈值算法进行比较发现，EMD消噪算法整体上不如小波阈值方法。本文分析了信号经EMD处理后各IMF分量特性，结合小波阈值去噪方法，充分发挥了两者的优点，实现了仿真信号和转子振动信号的去噪处理，并将其与EMD、小波阈值去噪方法做了比较分析，结果表明所提方法整体上优于EMD和小波阈值去噪方法。

1 改进EMD—小波分析原理及步骤

1.1 EMD—小波阈值降噪原理

以转子系统作为核心部件的大型旋转机械，在冶金、电力等行业发挥重要作用。然而，设备运行工况复杂，采集到得信号含有大量噪声，转子振动信号的数学模型可表示为

式中s(t)为转子振动信号，n(t)为噪声干扰，其中脉冲噪声和白噪声占主要成分[2]。

x(t)经经验模态分解后得到有限个频率由高至低的固有模态分量（Intrinsic mode function，IMF）分量，即

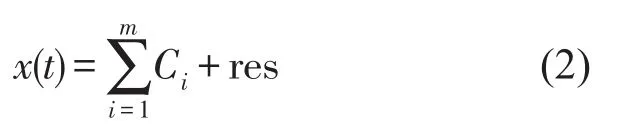
式中Ci表示各层IMF分量，res表示余项。

基于EMD去噪的主要思想是：被噪声污染的信号，有用信号的能量主要集中在低频段，越往高频段，含有的信号能量越少，因此，一定存在一个IMF分量，使得该分量之后的IMF中，信号为主导模态，而前面k个IMF分量中噪声为主导模态，对前k个IMF分量进行阈值量化处理，然后将提取的有用信号和余下的IMF分量叠加重构，便实现去噪。

为了进一步细致分析，将EMD处理含噪信号后得到的IMF分量分为三类：第一IMF分量（用imf1表示），高频IMF分量以及低频分量。通常认为第一IMF分量由噪声构成，但是随着研究深入，发现其含有一定量的信号细节信息[6,7]，为了提取其中的少量细节信息，提升去噪效果，本文对第一IMF分量进行大尺度小波分解，舍去全部高频的小波系数，只取低频小波系数进行重构，尺度越大，整体分离出的高频噪声越多，仅留少量的低频近似信号，则可认为低频近似部分中必然含有信号信息，予以保留。然后利用连续均方误差准则[8]consecutive mean square error，CMSE）对信号分量起主导作用模态与噪声起主导作用模态进行区分，将剩余的IMF分量分为高频IMF分量和低频IMF分量，高频分量中含噪较多的噪声成分，在小波阈值处理时可选取相对较小的阈值，尽可能多的剔除噪声成分。低频部分信号占主导成分，可选取较大的阈值，去除少量噪声的同时尽可能减少信号失真。

1.2 EMD—小波阈值降噪原理

文献[9]采用“3σ法则”实现了imf1中有用信息的提取，但是imf1中有用信息的含量是未知的，单纯将落在[-3σ1，3σ1]之外的信号认为是有用信息显然不妥。imf1中高频噪声起主导作用，而信号经小波大尺度分解可以将低频近似分量保留下来，从而将高频噪声分离出去，因此，本文利用大尺度小波分解实现imf1中的有用信息的提取。为了尽可能多的剔除噪声并保留信号细节，分解尺度的选取尤其重要。可以这样假设，若imf1经小波J+1层分解后，J层细节部分符合白噪声特性而J+1层细节部分不符合白噪声特性，可以认为从第J层开始，近似部分的有用信息被分离至细节分量，为了保留这部分有用信息，将分解层数设定为J。

本文使用自相关函数估计来进行白噪声特性检验。设序列xi(i=1，2，…，N)，其自相关函数的估计如式(3)

分解层数J确定之后，大部分高频噪声被分离到细节分量，因此，重构J层近似部分便可实现对imf1有用信息的提取。

1.3 EMD-小波阈值降噪原理

首先，需要对IMF分量进行高低频区分，噪声主要分布在高频IMF分量上，而信号主要分布在低频IMF分量上，因此可以利用连续均方误差准则对信号分量起主导作用模态与噪声起主导作用模态进行区分，即找到一个索引值js，使得从该索引开始往后的IMF分量对信号进行重构的误差最小。

其中N为信号长度，n为IMF分量的个数，IMF（ktl）表示第k个IMF的第tl个分量的重构误差，基于该准则，索引值js可由下式给出

argmin表示重构误差取最小的函数。不妨设imf2～imfk为除imf1之外剩余的高频IMF分量，imfk+1～imfm为低频IMF分量。对于噪声起主导作用的固有模态分量，在对小波分解后细节部分进行阈值处理时，需设定较大的阈值才能较为有效地去除高频噪声[11]，并且随着分解尺度的增加，信号小波变换的模极大值随之增加，而噪声小波变换的模极大值随之减小[12]，因此，阈值的设定需随分解尺度的增加而减小，综合以上分析，设定阈值为

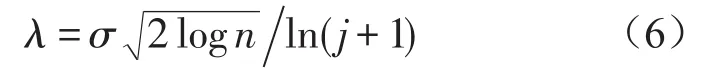
其中σ为噪声的标准方差，n为信号长度，j为分解尺度。

对于信号起主导作用的固有模态分量，在对小波分解后细节部分进行阈值处理时，需设定较小的阈值才能在有效去除高频噪声的同时，尽可能保留有用信号细节，减小信号失真，因此其阈值设定为

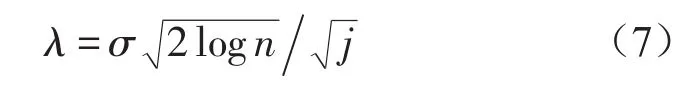
1.4 EMD—小波阈值降噪原理

综合以上分析，改进EMD—小波降噪具体步骤如下

(1)对含噪信号进行EMD分解，得到各模态分量imfi；

(2)对imf1进行J层小波分解，提取近似部分aJ。

(3)利用连续均方误差准则对信号进行高低频区分，设最后一个高频IMF分量为imfk，对imf2—imfk利用式（6）的阈值进行小波阈值处理中，σ为噪声的标准方差，n为信号长度，j为小波分解尺度。对imfk+1～imfm阈值处理时根据式（7）选取阈值.

(4)将（2）（3）提取的有用信号细节和余项res叠加重构，即为去噪后的信号。

2 仿真实验及分析

为了验证所提方法的有效性，利用去噪分析算法的标准信号和实测轴承振动信号进行验证分析，采用信噪比、均方误差评估算法性能。

2.1 EMD—小波阈值降噪原理

利用Matlab中的wnoise函数生成的“Blocks”，“Bumps”，“Heavy sine”和“Doppler”测试信号进行分析，信号的长度取2 046，信噪比为2 dB时生成的含噪信号波形如图1所示。

图1 用wnoise产生的含噪信号

图2为小波分析去噪结果图，其中小波基函数都选用“db 5”小波函数，并且进行3层小波分解，采用软阈值方法，阈值采用自适应史坦（Stein）无偏估计得到。

图2 小波分析去噪结果

图3为EMD去噪结果图，其中包括9个IMF分量和一个余项res。图4为本文方法的去噪效果图，第一层IMF分量绝大部分是噪声，所以选定较大的分解层数5，以便尽可能多地将噪声分离出去。利用连续均方误差准则对信号进行高低频区分，经计算k=4，对imf2—imf4采用“db 5”基小波进行3层分解，阈值函数采用软阈值，阈值由式（7）确定，而imf5—imf9阈值由式8确定。经比较本文方法有效地抑制了噪声，较好地恢复了信号原貌，处理后的波形图也较小波分析和EMD平滑。表1给出了三种方法处理后信号的信噪比（SNR）和均方误差（MSE）的对比，可以看出，小波分析去噪方法要稍优于EMD去噪方法，而本文所提方法处理后信号的均方误差最小，且将信噪比提高了近2 dB，说明本文方法要优于小波去噪方法和EMD去噪方法。

图3 EMD去噪结果

图4 本文方法去噪结果

2.2 EMD—小波阈值降噪原理

将提出的降噪方法应用于转子振动信号的降噪，轴承转速为2 700 r/min，采样频率为10 kHz，数据长度为40 000，其实测波形图如图5所示，轴心轨迹如图7所示。受到复杂噪声干扰，从时域图中很难准确提取信号特征，当转子出现横向裂纹时，转子会出现扭振现象，扭振信息以相位调制的形式存在于转子的振动信号中形成调相信号。相位调制在时频图上表现为信号的频率调制，并且频率和转子频率相同，利用该特征可判断裂纹故障的存在，可区分转子不对中等相似特征的故障[1]。图6是本文方法的去噪结果，对比图5可知，信号得到了降噪，特征清晰，可以看出，前10 000个点信号出现小幅值波动，而后30 000个点信号稳定运行，是由于开机转速不稳定所致。图8为去噪后信号的轴心轨迹，原始信号中噪声成分明显被抑制，转子的运行状态特征清晰明显，符合正常状态时的情形[13]，主要是所提方法能够充分提取各层IMF分量中的噪声成分，并最大幅度保留信号的真实信息，有非常好的应用价值。

图5 实测转子振动信号

图6 本文方法去噪结果

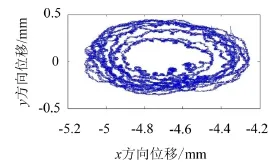
图7 实测转子振动信号轴心轨迹

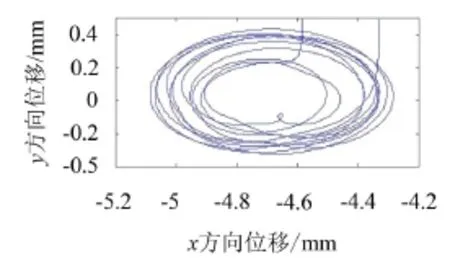
图8 去噪后转子振动信号轴心轨迹

表1 三种方法去噪结果比较

3 结语

针对低信噪比非线性信号去噪效果不理想，提出了改进EMD—小波分析相结合的去噪方法。分析了信号经EMD分解后各IMF分量的噪声分布特性，根据噪声含量大小自适应设定阈值。然后，利用小波分析对高低频IMF分量进行有用信号的提取，将提取的信号和低频IMF分量叠加重构，实现降噪。进行了数字仿真和转子振动信号降噪分析，结果表明，所提方法整体上优于EMD和小波阈值去噪方法。

[1]陈仁祥，汤宝平，吕中亮.基于相关系数的EEMD转子振动信号降噪方法[J].振动、测试与诊断，2012，32（4）：542-546.

[2]王秉仁，杨艳霞，蔡伟，等.小波阈值降噪技术在振动信号处理中的应用[J].噪声与振动控制，2008，6：9-12.

[3]Tejas H P,Ashish K D.Coupled bending-torsional vibration analysis for rotor with rub and crack[J].Journal of Sound and Vibration,2009,326(3-5):740-752.

[4]陈果.一种转子故障信号的小波降噪新方法[J].振动工程学报，2010，20（3）：285-290.

[5]Boudraa A O,Cexus J C.De-noising via empirical mode decomposition[C].Proceedings of the IEEE International Symposium on Control Communications and Signal Processing,Marrakech,Morocco:IEEE,2006:4-8.

[6]曲从善，路延镇，谭营.一种改进型经验模态分解及其在信号消噪中的应用[J].自动化学报，2010，36(1)：67-73.

[7]HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London Series A-Mathematical Physical and Engineering Science,1998,454: 903-995.

[8]Donoho D L.De-noising by soft-thresholding[J].IEEE Trans.On IT,1995,41(3):613-627.

[9]曲从善，路延镇，谭营.一种改进型经验模态分解及其在信号消噪中的应用[J].自动化学报，2010，36(1)：67-73.

[10]李炜，陈晓辉，毛海杰.小波阈值消噪算法中自适应确定分阶层数研究[J].计算机仿真，2009，26（3）：311-313.

[11]韩敏，刘玉花，席剑辉，等.基于小波变换阈值决策的混沌信号去噪研究[J].信息与控制，2005，34(5)：543-547.

[12]张旭东，詹毅，马永琴.不同信号的小波变换去噪方法[J].石油地球物理勘探，2007，42(S)：118-123.

[13]邓林峰，赵荣珍，龚俊.一种改进的转子振动信号消噪方法研究[J].仪器仪表学报，2011，32（9）：1961-1965.

4 结语

通过对发动机故障模拟试验台采集发动机振动信号，并借助小波理论对信号进行消噪，提取特征值。运用模糊神经网络对发动机故障进行了诊断，充分利用了神经网络和模糊系统的各自优点，实现了优势互补，在应用中得到了很好的故障诊断效果。相比于传统的BP神经网络诊断方法，无论在诊断精度上还是诊断速度上，模糊神经网络更具优势，为复杂系统的故障诊断提供了有效的工具。

参考文献：

[1]段伟武，宋宜斌.基于自适应神经网络模糊推理系统的柴油机故障诊断[C].第二十九届中国控制会议论文2010：3842-3845.

[2]李国勇，杨庆佛.基于模糊神经网络的车用发动机智能故障诊断系统[J].系统仿真学报，2007，(3)：1034-1037.

[3]王生昌，赵永杰，许清杰.基于自适应模糊神经网络的故障诊断方法[J].汽车工程，2006，28(4)：398-400.

[4]赵晓燕.改进的小波阈值函数滤波分析[J].噪声与振动控制，2013，(2)：117-127.

[5]杨超，王志伟.基于小波分析和模糊神经网络的齿轮故障诊断研究[J].噪声与振动控制，2010，(4)：64-68.

[6]彭斌，刘振全.基于改进小波神经网络的旋转机械故障诊断[J].振动、测试与诊断，2007，27(1)：32-35.

Denoising of Rotor Vibration Signals Based on Improved EMD-WaveletAnalysis

LI Lin,ZHANG Yong-xiang,LIU Shu-yong
（College of Power Engineering,Naval University of Engineering,Wuhan 430033,China）

A method based on EMD and wavelet analysis was proposed for denoising of low SNR rotor vibration signals.Firstly,the noise signal was decomposed by EMD,and the IMF components were classified into high-frequency components and low-frequency components according to consecutive mean square error(CMSE)criterion.Then,different thresholds were determined and the useful signals of high and low frequency IMF components were extracted respectively based on the wavelet analysis.The extracted signals were superimposed with the low-frequency IMF components and reconstructed so that the noise of IMF was removed efficiently.Numerical simulation and rotor vibration signal analysis were carried out to evaluate the performance of the proposed method.The results show that the proposed method is better than the individual EMD or wavelet threshold denoising algorithm.

vibration and wave;chaos signal;EMD;wavelet analysis;CMSE

O322

A

10.3969/j.issn.1006-1335.2015.02.038

1006-1355(2015)02-0170-05

2014－08－16

李琳(1979－)，男，辽宁抚顺人，博士，从事机械设备状态监测。E-mail:daweill1@hotmail.com