用小型传声器阵列测量环境噪声中简单声源声压级
宋玉来,岳 磊,金江明,卢奂采
(1.浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室,杭州 310014;2.浙江中科电声研发中心,浙江 嘉兴 314115)
用小型传声器阵列测量环境噪声中简单声源声压级
宋玉来1,岳 磊2,金江明1,卢奂采1
(1.浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室,杭州 310014;2.浙江中科电声研发中心,浙江 嘉兴 314115)
常规声级计测量到的是目标声和环境噪声的总声压,不具备抑制环境噪声的功能。为此使用以球面波函数叠加逼近理论为基础的声波分离方法,用以提升环境噪声中简单声源声压级的测量精度。该方法以小型传声器阵列探头作为测量前端,近场声全息和声波分离为核心计算方法进行实施。为验证该方法的有效性,在全消声室内对关键参数进行了实验验证。实验结果表明,该方法在500 Hz~2 750 Hz频带内,且探头距目标声源5 cm~12 cm的近场区域,可以在环境噪声中得到较精确的目标声源的声压级。
声学;声波分离;小型阵列探头;球波函数叠加;声压级测量;近场声全息;
声级计作为现场声压测量的重要工具,具有操作简便快速的优点,可以实时的测量声场中任意一点的声压值[1]。然而,当声场中除了目标声源外还有其它干扰噪声源存在时,声级计测量到的声压大小无法反映目标对象辐射的真实声压,甚至得到错误的测量结果。
在近场声全息[2,3]研究领域,可以利用声波分离方法来减弱干扰噪声源对声压测量值的影响,实现有噪声干扰情况下对目标声源声压测量。现有的声波分离方法在实施过程中主要涉及两种测量方式:双层阵列声压测量[4,5]及单层阵列声压—空气粒子速度测量[6,7],前一种测量方法要求在声场中布置存在精确相对位置关系的两层阵列,而后一种测量方法虽然只需要单层的阵列,但是必须同时得到阵列上测点处的复声压信号及空气粒子振速信号。这两种声波分离方法尽管能够实现噪声干扰环境下的目标声信号测量,但所需的测点数量较多,常常需要几十个测点。因此上述方法由于实际操作复杂和较高的硬件成本而不适用于噪声环境下声压的快速准确测量。
针对以上问题,文中使用一种基于小型传声器阵列探头的声波分离方法[8]抑制噪声源的干扰,以达到提高声压测量精度的目的。该方法以球面波函数扩展叠加理论[9,10]为基础,将测点处的复声压表达成一系列球面波基函数叠加的形式,通过分离描述不同传播方向声波的基函数项并重构声场,进而分离掉一部分阵列探头背向的干扰噪声。在此理论基础上,自行设计了五测点立体传声器阵列探头,对影响该声波分离方法的主要参数进行了实验研究。根据实验结果,给出了该方法的适用条件及提高分离精度的途径。
1 声波分离理论
小振幅振动产生的声波在空气介质中的传播规律可用波动方程加以描述,三维波动方程经傅里叶变换后的表达,称为Helmholtz方程。在球坐标系下,Helmholtz方程[11]可写为
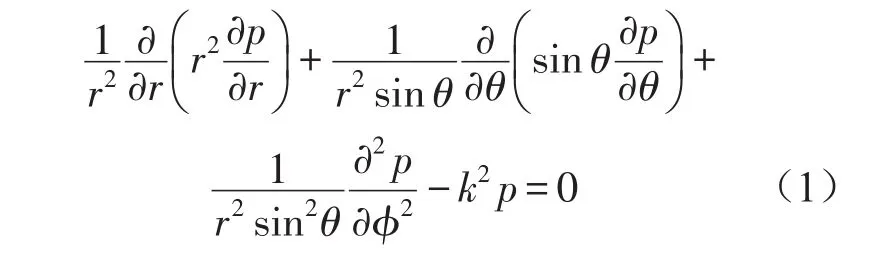
由于球面波函数可以较好地描述一个封闭目标声源向外界辐射声场的物理模型,且可以抑制局部全息测量面边缘导致的空间窗口效应[12],于是以球波函数作为基函数,使用分离变量法求解(1)式,可得声场中任意一点(r,ϕ,θ)处的复声压为
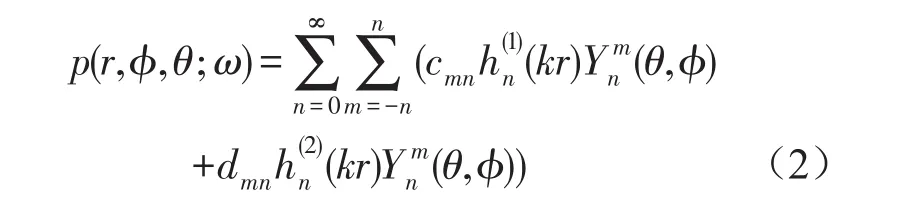
其中球谐函数定义式为
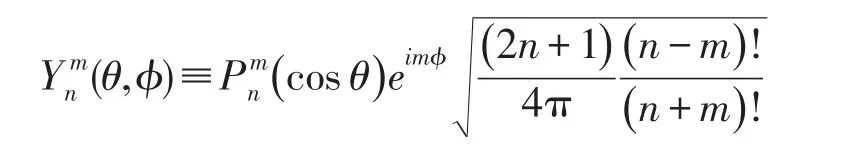
其中,ω为角频率;k=ω/c为波数(c为声音在空气中的传播速度);和分别为n阶第一、二类球Hankel函数;随着r的增大而呈指数衰减,可描述由目标声源向外辐射的声波(即去波,Outgoing wave);随着r的增大而呈指数增长,可描述由干扰声源向目标声源方向传播的声波(即来波,Incoming wave),如图1所示。通过求解每项基函数的系数cmn和dmn便可重建目标声源独自产生的声压。
理论上,当n趋向于无穷大时,(2)式所得声压解即为精确解。由于球面谐波函数的高阶项代表的是小幅度的声场分量,其贡献不能传递到远场,测量面上的传声器很难分辨出如此小幅度声波的存在,所以(2)式右侧的高阶项可以被忽略[13],只取低阶前N项基函数,N为有限整数值。为了获取反映声场特征的系数向量,需要一定数量的测量点M,测点数可以大于、等于或者小于基函数的项数,分别对应线性系统为超静定、静定和欠静定的传递矩阵。为了求解方便及准确,一般使测点数等于基函数的项数,即M=N。通过将测点处的声压表达成球面谐波叠加的形式,并求解以方程(2)为基础的线性系统,即可求得复系数cmn(ω)和dmn(ω),进而通过复系数重构声场中任意点声压的近似解。
如图1所示,直角坐标系中布置有两个声源,分别为需要进行辐射声压测量的目标对象(称为目标声源)及阵列探头背向的声源(称为干扰声源),空间中分布的声源可以为形状规则的球形声源,也可以为不规则的非球形。对于非球形的声源,需将坐标系原点设在目标声源的中心,即位于能包络整个声源的最小球面的球心处。干扰声源的中心位于Z轴上。D1与D2分别表示阵列探头中心测点与目标声源与干扰声源之间的距离。两声源中间是自行设计的五测点传声器探头,探头如图2所示。
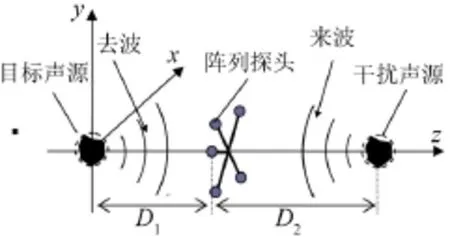
图1 各声源与阵列探头的位置分布示意图

图2 阵列探头测点分布尺寸示意图
对于图1中的五测点传声器阵列探头,可设去波、来波分量对应的基函数各展开 N1、N2项(N1+N2=5),令为第i个测点的第 j项描述去波成分的基函数,为第i个测点的第 j项描述来波成分的基函数,并将每个测点坐标进行坐标变换到球坐标系下,可得:


上式左边为各传声器上的测量复声压,求解(4)式即可获得表征声场特征的复系数。通过去波基函数项的系数cj就可重构得到声场中去波在测点处的声响应,即目标声源在测点处产生的近似声压,可写为

由于分离方法在实施中只使用了5个传声器,可用的球面谐波叠加项数受到限制。所以,上述方法适用于简单声源,复杂声源声场分离效果欠佳,但可通过增加传声器数量的方式进一步提高分离精度。对于高度非球形的平面声源,可根据文献[14]建议的布置进行分离。此外,当强背景噪声存在时,目标声源的声信号会被噪声所淹没,此时不宜实施所述方法;由于所建立的物理模型是针对干扰声源和目标声源分别位于测量面的两侧,所以在方法的实施过程中,应避免将其用于干扰声源和目标声源同侧的声场。
2 实验条件及实验步骤
为了验证小型传声器阵列探头的声波分离的效果,在全消声室内进行了分离实验研究。实验室本底噪声为18 dB(A),截止频率为63 Hz,实验装置在消声室中的布置如图3所示。所用到的实验设备主要有:两个相同型号的小型扬声器,丹麦B&K公司的6通道3050-A-060数据采集模块及3160-A-042发声模块各一个,2176C型功率放大器,5支B&K公司4958型1/4英寸传声器,自行设计的五测点立体传声器阵列,2个声源固定支架,1个探头固定支架,笔记本一台。

图3 阵列探头分离声波技术实验装置实物图
五测点立体阵列探头的测点分布尺寸如图2所示,这种立体型阵列探头相比平面探头可以更好的捕捉声场信息,且各测点通过形成一定的空间指向性来获取波前的传播方向等信息。包络图3左侧扬声器(目标声源)外轮廓的最小球面中心位于坐标系原点处,干扰声源的中心位于(0,0,0.3 m)。传声器阵列探头正对于目标扬声器声源,且中心测点与目标声源中心的距离为D1。之所以选用扬声器作为实验中的声源,是因为扬声器的声场具有一定的代表性,且已被多次用于相关理论的实验验证[15,16]。
实验过程中,首先设定目标声源与干扰声源同时发出相同频率相同幅值的正弦信号,待声场稳定后,通过数据采集模块采集5 s声压信号,随后在PULSE Labshop软件中对时域信号进行快速傅里叶变换处理,得到频域上的声压数据(即分离前声压)。在其它条件不变的情况下,仅将干扰噪声关闭,使用同样方法得到目标声源单独在各测点处产生的声压信号,以此作为考察分离精度的无干扰声压值。最后对分离前的声压进行声波分离处理,得到各测点处分离后的声压值,通过对比分离前后声压值与无干扰声压值的大小关系,验证分离方法的有效性。
3 实验数据处理
3.1 考察频率对分离精度的影响
根据空间采样定理和小型阵列扬声器探头的尺寸选300 Hz~3 000 Hz为分析频带。实验过程中保持测量距离D1=10 cm不变,从小到大依次选择具有代表性的频率作为所考察的声源频率。当所分析频率为 f=1 250 Hz时,实验分离前后的结果对比如图4所示。
由图4的实验结果可知,分离前声压值相对于无干扰声压值有较大的误差,而分离后的结果则能够相对较好的反映出无干扰声压值。特别是在③号测点处,无干扰声压值为0.245 Pa,没有经过分离算法处理的声压值约为0.41 Pa,该点处相对误差达到67%,而分离后的声压几乎等于无干扰声压值,即解决了由声源干涉现象产生的测量值失真问题。

图4 D1=10cm,f=1 250 Hz时各测点处的分离结果
由于分离算法中,③号测点更能反映声波分离的效果,另外四个测点的主要是用于提高③号测点的分离精度,且考察的频率数较多。所以,此处只给出③号测点(即中央测点)处不同频率时的声压分离效果。不同频率下声波分离前后对比曲线图如图5所示。
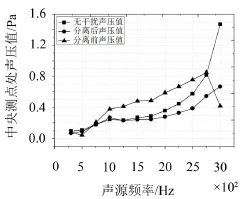
图5 D1=10cm时,③号测点处不同频率下声波分离
前后声压值对比曲线
从图5可看出,分离后声压值曲线在1 500 Hz以下的较低频带可以与无干扰声压值曲线保持较好的一致。随着频率的增加,分离后声压值与无干扰值的偏差也越来越大,当分析频率处于2 250 Hz到3 000 Hz频段内时,所用分离方法失效。事实上,受到香农空间采样定理的限制,分离效果在很大程度上取决于阵列探头上测点的间距,当间距减小时,可以改善该方法在高频处的应用效果。
另外,为了定量地综合评价探头上所有测点处的声压分离效果,现引入二范数误差计算式

无干扰声压值的误差,如图6所示。

图6 D1=10cm时,分离前后声压的二范数误差曲线
由图6可看出,在500 Hz~2 750 Hz频率范围内,分离方法可以在整个阵列探头上得到相对分离前较小的声压二范数误差,且随着频率的增加,该分离误差逐渐增大,且其增大趋势与图5中单测点处分离后声压曲线较为一致。可见,在所示分析频段内,相同尺寸声源发出的不同频率的声波,所述方法更适用于相对较低频率的声波分离。这是因为相对较低频率声波的指向性没有较高频率声波的指向性强,即较低频率声波的波前更接近于球面波,更有利于使用球面谐波函数的叠加准确描述声场。
3.2 考察测量距离对分离精度的影响
测量阵列距离目标对象的远近,直接影响到测量信号的受干扰程度。为了考察测量距离对分离结果的影响,实验过程中保持声源频率 f=1 000 Hz不变,依次考察测量距离D1从5 cm开始以1 cm间距递增到15 cm时的分离效果,分离前后③号测点处声压的分离效果如图7所示。
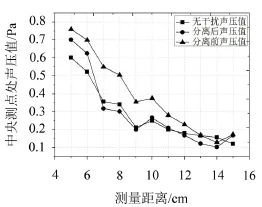
图7 f=1 000 Hz时,③号测点处分离前后声压值曲线
由图7可知,在5 cm~12 cm测量距离的范围内,③号测点处分离后声压值曲线更加接近于无干扰声压值,而在D1≥13 cm的区域则得不到积极的分离结果。事实上,由于分离方法所用的理论基础为球面近场声全息方法,因此,在应用过程中也要尽量满足近场声全息的应用条件,即测量过程需要在目标声源的近场进行,以得到更为丰富的声源所发出的倏逝波信息。
为了更为方便的看出分离效果,使用(8)式分别计算不同测量距离下分离前后声压值相对于无干扰值的二范数误差,如图8所示。

图8 f=1 000 Hz时,分离前后声压的二范数误差曲线
由图8中的二范数误差曲线可看出,当f=1 000 Hz时,对于d>12 cm的测量距离,分离后误差随着距离的增加而明显增大,而在5 cm~12 cm之间则能够得到有效的分离结果,该结果与图7中的单点声压分离结果较为一致。所以,分离后的值可用于提高噪声环境下声压级的测量精度,尽管分离方法能够降低干扰噪声,但为了更为准确获取目标声源的声场信息,实际测量时仍不能将传声器阵列放得距目标对象过远。
4 结语
针对噪声环境下常规声压级测量方法无法准确测量的局限,使用一种以球波函数叠加逼近理论为基础,以小型传声器阵列探头为测量工具的声波分离方法。基于已建立的分离理论模型进行了实验研究,分别考察了分离方法对300 Hz~3 000 Hz内不同频率声波、5 cm~15 cm不同测量距离的分离效果。实验结果表明该方法在500 Hz~2 750 Hz的频段内,及5 cm~12 cm的目标声源近场内可以得到较好的分离效果。所述方法的实施过程简单,可在噪声环境下声压级的准确测量提供参考。
[1]钱小平,郝点,陈兰英.往复压缩机噪声测试分析[J].噪声与振动控制,2010,30(3):164-167.
[2]Williams E G,Maynard J D,Skudrzky E.Sound source reconstructions using a microphone array[J].Journal of the Acoustical Society ofAmerica,1980,68(1):340-344.
[3]Williams E G,Dardy H D,Fink R G.Nearfield acoustical holography using an underwater automated scanner[J]. Journal of the Acoustical society of America,1985,78 (2):789-798.
[4]Cheng M T,Mann J A,Pate A.Sensitivity of the wave-number domain field separation methods for scattering[J]. Journal of the Acoustical Society of America,1996,99 (6):3550-3557.
[5]于飞,陈剑,毕传兴,等.双全息面声场分离技术的实验研究[J].声学学报,2005,30(5):452-456.
[6]Jacobsen F,Jaud V.Statistically optimized near field acoustic holography using an array of pressure-velocity probes [J].Journal of the Acoustical Society of America,2007, 121(3):1550-1558.
[7]Zhang Y B,Chen X Z,Jacobsen F.A sound field separation technique based on measurements with pressure-velocity probes[J].Journal of the Acoustical Society of America,2009,125(6):3518-3521.
[8]岳磊,金江明,宋玉来,等.基于小型阵列探头的声波分离方法研究[J].电声技术,2014,38(4):37-44.
[9]Wu S F.On reconstruction of acoustic pressure fields using the Helmholtz equation least squares method[J].Journal of the Acoustical Society of America,2000,107(5): 2511-2522.
[10]Wu S F.Methods for reconstructing acoustic quantities based on acoustic pressure measurements[J].Journal of the Acoustical Society of America,2008,124(5):2680-2697.
[11]Williams E G.Fourier acoustics:sound radiation and nearfield acoustical holography[M].San Diego:Academic press,1999.183-186.
[12]Sean F W,Natarajan L K.基于Helmholtz方程最小二乘法声全息复杂结构振动噪声响应分析[J].汽车工程学报,2011,1(4):237-247.
[13]Rayess N,Wu S F.Experimental validations of the HELS method for reconstructing acoustic radiation from a complex vibrating structure[J].Journal of the Acoustical Society ofAmerica,2000,107(6):2955-2964.
[14]Lu H and Wu S F.Reconstruction of vibroacoustic responses of a highly nonspherical structure using Helmholtz equation least-squares method[J].Journal of the Acoustical Society ofAmerica,2009,125(3):1538-1548.
[15]Bi C X,Chen X Z,Chen J.Sound field separation technique based on equivalent source method and its application in nearfield acoustic holography[J].Journal of the Acoustical Society ofAmerica,2008,123(3):1472-1478.
[16]Semenova T,Wu S F.On the choice of expansion functions in the Helmholtz equation least-squares method[J]. Journal of the Acoustical Society of America,2005,117 (2):701-710.
Measurement of Sound Pressure Level of SimpleAcoustic Sources in Noisy Environment with Mini-sized MicrophoneArrays
SONG Yu-lai1,YUE Lei2,JIN Jiang-ming1,LU Huan-cai1
(1.Key Laboratory of E&M,Ministry of Education&Zhejiang Province, Zhejiang University of Technology,Hangzhou 310014,China; 2.Zhejiang Electro-Acoustic R&D Center,Jiaxing 314115,Zhejiang China)
Generally,conventional sound-level meters can only measure the total sound pressure of the target sound source and the environment noise instead of measuring them separately.To improve the measurement accuracy of the sound pressure level of the target sound source in noisy environment,the acoustic wave separation method based on spherical wave superposition was used with the input of the acoustic pressures measured by a mini-sized microphone array.The impact of parameters on the accuracy of the sound pressure level was examined in an anechoic chamber.The results show that a reasonable accuracy can be obtained when the frequency is ranged from 500 Hz to 2 750 Hz and the measurement distance is from 5 cm to 12 cm.
acoustics;acoustic wave separation;mini-sized array;spherical wave superposition;sound pressure level measurement;near-field acoustic holography
O42 2.2
A
10.3969/j.issn.1006-1335.2015.02.032
1006-1355(2015)02-0141-05
2014-09-11
国家自然科学基金资助项目(51275469;51205354)
宋玉来(1987-),男,安徽六安人,博士生,主要研究方向:从事基于阵列信号处理的声源识别定位和声波分离方法研究。E-mail:songyulai_svlab@163.com
卢奂采,女,教授,博士生导师。E-mail:huancailu@zjut.edu.cn

