工程施工索赔博弈决策研究——以电力工程施工为例

李 丹

国网江西省电力公司宜春供电分公司 江西 宜春 336000

0 引言

工程施工索赔是指在履行施工合同过程中，合同相关当事人因非自身原因而受到实际损失或权利损害时，通过合法程序向对方提出经济或时间补偿的要求［1］。工程施工索赔是法律通过合同形式赋予受损失者的应保护的权利，是保护受损失者自身利益的重要手段，对其处理的好坏也直接反映了一个企业的管理水平。

在实际工程施工索赔案例中，由于业主的发包优势地位，一般业主主动索赔的案例比例较少，而且处理方便。最常见且处理比较困难的是：承包商向业主的索赔。工程施工索赔问题实际上是索赔双方的行为相互作用的对策及均衡的问题。国内相关学者已经从承包商的角度出发，根据工程施工索赔的特点，应用博弈理论建立了各自的索赔博弈模型，并分析了不同条件下业主和承包商的选择和行为，如文献［2-4］。有学者则基于水电工程特点，建立了承包方、监理和业主三方的索赔博弈模型，并分析了水电工程中索赔三方在不同条件下的选择和行为［5］。

以上相关研究为承包方向业主索赔提供了很大决策支持，但是新版《电力建设工程标准施工招标文件》中索赔处理程序存在了一些变化；同时，现实中可能存在恶意索赔及恶意拒绝无限制性条件的可信性问题；另外，传统决策支持模型中支持承包商积极开展诉讼或仲裁的成功率值等参数往往不容易获得，导致很多决策支持模式无法实施，需要进一步修正。本文正是基于以上问题，主要从承包商的角度，以2013年版《电力建设工程标准施工招标文件》为基础，应用博弈理论，尝试建立承包商向业主的施工索赔博弈决策支持模型。

1 2013版《电力建设工程标准施工招标文件》索赔处理程序

如图1所示：

图1 电力建设工程施工索赔流程图（根据2013版《电力建设工程标准施工招标文件》绘制）

2 电力建设工程施工索赔的博弈模型

2.1 相关概念

博弈是指人、团队或其他组织面对特定环境，在一定约束下，依靠所掌握的信息，先后或同时，一次或多次，基于不同决策者的可能行为或策略进行决策选择，并各自获得最优结果或收益的过程。

博弈论要求按照特定的时间顺序和信息要求，所以时间顺序和信息是影响博弈均衡的主要因素。在博弈过程中，参与者之间的信息传递决定了其行动空间和最优战略的选择；同时，博弈过程中始终存在一个先后时间顺序，参与人的行动次序对博弈最后的均衡有直接的影响。

按照参与人行动次序和其对其他参与人所掌握的信息完全度进行分类，博弈决策环境可以分为：完全信息静态博弈、完全信息动态博弈、不完全信息静态博弈和不完全信息动态博弈四种。

2.2 电力工程施工索赔博弈决策模型

从博弈论视角，电力建设工程施工索赔具有非合作性、动态性、序贯性的特征。它们是在承包商和业主双方理性的前提下，各自做出的最优决策。

根据电力工程施工索赔的特点和博弈论的应用范围，我们建立了如图2的工程电力工程施工索赔博弈决策模型。

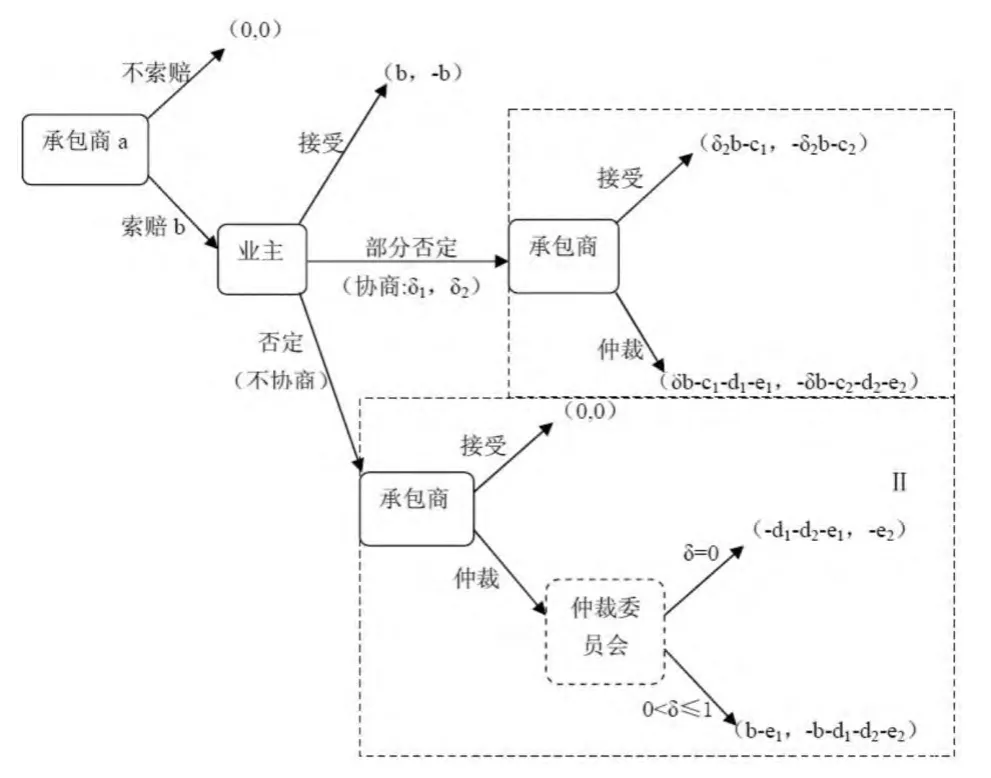
图2 电力建设工程施工索赔决策博弈树

图2中承包商受干扰因素影响发生可能额外支出或损失a；承包商为此提出的实际索赔额为b；承包商谈判成本记为，则为业主谈判成本；为承包商实施仲裁的成本，为业主实施仲裁的成本；为承包商实施仲裁的机会成本，则为业主响应仲裁的机会成本；代表承包商在谈判未主张调整系数（即贴现因子），为业主在谈判未主张调整系数，δ是仲裁庭的裁决调整系数。

在子博弈Ⅰ中，我们假设承包商和业主已进行了充分的谈判，并且双方都做出了必要的努力，如果仍然无法达成索赔协议，需要进行仲裁，则仲裁成本由承包商和业主双方各自承担，这样可以对承包商和业主双方均有一定的制约作用。

在子博弈Ⅱ中，考虑到仲裁费时、费力且费钱，很多索赔往往都是不能或不值得递交至仲裁庭的，同时考虑到业主及工程师的信誉、公正性等问题，我们从承包商的角度出发，出于遏制业主及工程师拒不承认承包商合理索赔的情形，我们加入可信性条件，所以在此博弈路径下，承包商和业主双方的仲裁成本又继续分叉为δ=0及0＜δ＜≤0的两种情况。

另外，考虑到业主对承包商索赔的“部分”或者“全部否定”后，承包商需要首先选择谈判或不谈判。如果承包商提出谈判要求，业主又可能要选择谈判或不谈判，此时由于单方面出现不愿谈判将导致的直接进入仲裁，进入“否定”“仲裁”域；由于单方面不愿谈判又可能导致的承包商接受 “部分否定”、“接受”，此时 δ=0。

2.3 电力建设工程施工索赔的完全信息动态博弈

我们假定承包商、业主均为风险中性，且双方在对于干扰事件的认定上是信息完全对称的（即符合完全信息动态博弈条件），所以：

对于完全合理索赔，即进入到裁决δ=1的索赔仲裁阶段：在此情形的第三阶段承包商会选择“否定 （不协商）”、“仲裁”， 此时业主的收益-b---＜-b，故在第二阶段业主会选择接受，在第一阶段承包商会选择“索赔”，所以，此时的子博弈精炼纳什均衡为：承包商“索赔”，业主“接受”，博弈结束，收益组合为（b，-b）。但是，现实中，这种直接、全部地认可索赔要求的情况是极少的。

对于完全无理索赔，即进入到裁决δ=0的索赔仲裁阶段：在此情形的第三阶段承包商会选择“接受”，此时业主的收益 0＞-b 并且 0＞-b-，故在第二阶段业主会选择“否定”，在第一阶段承包商会选择“不索赔”，所以，此时的子博弈精炼纳什均衡为：承包商“不索赔”，博弈结束，收益组合为（0，0）。

事实上，绝大多数索赔往往都会存在争执，一般都需要经过友好协商的过程。所有在子博弈Ⅰ中，由于分别为承包商和业主在充分谈判后提出的调整系数，可认为具有相当的地位，可推出δ的期望为（+）／2。

当（-）b／2--＞0 时，在此情形下的第三阶段，承包商会选择“仲裁”。

当-（+-2）b／2---＞0 时，在此情形下的第二阶段业主会选择“部分否定”，在第一阶段承包商会选择“索赔”，所以，此时的子博弈精炼纳什均衡为：承包商“索赔”，业主“部分否定”，承包商“仲裁”，博弈结束，收益期望为（（+）b／2---，-（+）b／2---）。

当-（+-2）b／2-c2--＜0 时，在此情形下的第二阶段业主会选择“接受”，在第一阶段承包商会选择“索赔”，所以，此时的子博弈精炼纳什均衡为：承包商“索赔”，业主“接受”，博弈结束，收益为（b，-b）。

当（-）b／2--＜0 时，在此情形下的第三阶段承包商会选择“接受”。

当（1-）b-＞0时，在此情形下的第二阶段承业主会选择“部分否定”，在此情形下的第一阶段承包商会选择“索赔”，所以，此时的子博弈精炼纳什均衡为：承包商“索赔”，业主“部分否定”，承包商“接受”，博弈结束，收益为（b-，-b-）。

当（1-）b-＜0时，在此情形下的第二阶段承业主会选择“接受”，在此情形下的第一阶段承包商会选择“索赔”，所以，此时的子博弈精炼纳什均衡为：承包商“索赔”，业主“接受”，博弈结束，收益为（b，-b）。

3 实例分析

某供电建设工程，工程施工期不到3年，原合同价2500万元，但种种原因，在合同实施中承包商提出许多索赔，总值达2000万元。工程师作出处理决定，认为补偿1200万元比较合理。业主愿意接受工程师的决定。但承包商不肯接受，要求补偿1800万元。

由于双方达不成协议，承包商向国际商会提出仲裁要求。

分析：本例中，索赔产生争执，在谈判末期，业主主张补偿1200万，承包商主张补偿1800万，承包商进入本文工程施工索赔博弈模型的子博弈Ⅰ。此时，承包商要进行分析、判断、决策。承包商首先要考察判别条件（-）b／2--＞0 是否成立，其中（-）b／2=1500万元，由于该索赔采用国际仲裁，资料表明，在巴黎进行国际仲裁平均要18个月，最终索赔解决费用一般都超过索赔要求25%以上，所以仲裁费用可最低估算为1800／4／2=225万元，而机会成本则包括了承包商的经营战略成本、资金流通性成本、资金时间成本等等，当估算＞75万元时，承包商应该提请仲裁，当估算≤75万元时，承包商应该接受业主补偿1200万元。

4 结语

电力建设工程施工索赔是一项涉及面广，所需知识多的工作，涉及工程技术、经营管理、合同管理及法律等各方面的知识，对承包商的要求较高。它要求我们科学梳理施工索赔的处理程序，建立了科学的施工索赔的博弈模型，并全面分析了不同情况下承包商与业主的可能选择和行为，从而做出明智的决策。

［1］成虎.建设工程合同管理与索赔［M］.南京：东南大学出版社，2008.

［2］韩晓冬，罗汀.基于博弈模型的工程索赔决策研究［J］.建筑经济，2008（12）：29-31.

［3］洪伟民.建设工程索赔决策的博弈分析［J］.港工技术，2008（2）：37-39.

［4］陈伟，黄有亮.工程索赔过程的博弈分析［J］.基建优化，2007（5）：39-41.

［5］贾立敏，曾露，田志超.水电工程索赔的三方博弈分析［J］.水利经济，2010（3）：63-70.