IM分担两个值的亚纯函数
徐琳,牛红玲
(河北民族师范学院数学与计算机系,河北承德067000)
IM分担两个值的亚纯函数
徐琳,牛红玲
(河北民族师范学院数学与计算机系,河北承德067000)
主要研究亚纯函数及其n阶导数的分担值问题,改进了仪洪勋、杨重骏等人的定理,得到了以下结论:设f,g为开平面上两个非常数亚纯函数且IM分担∞,f(n)与g(n)IM分担1,n为正整数,如果(4n+7)Θ(∞,f)+4δ(0,f)+2δ (0,g)>4n+12,则f≡g或者f(n)·g(n)≡1.
亚纯函数;唯一性;IM分担值
1 引言及主要结论
本文所使用值分布理论[1,2]的标准记号,如T(r, f),m(r,f),N(r,f),(r,f),和,以及表示亏量的δ(0,f),Θ(∞,f)等等,(参考[1],[2]),这里不再赘述.对于复数α,如果f和g具有相同的α-值点,并且重数也相同,就称f和g CM分担a;如果f和g具有相同的α-值点,不计重数,就称f和g IM分担α.
1976年,杨重骏[7]提出如下问题:设f与g为开平面上两个非常数整函数,以0为CM公共值(分担值),f′与g′以1为CM公共值.问f与g之间有何种关系?
1989年,仪洪勋[8]回答了杨重骏提出的上述问题,证明了下面定理:
定理A[8]设f与g为两个非常数整函数,以0为CM公共值,f′与g′以1为CM公共值,如果δ(0,f),则f≡g或者f′·g′≡1.
更一般的,仪洪勋证明了:
定理B[8]设f与g为两个非常数整函数,以0为CM公共值,f(n)与g(n)以1为CM公共值,n为正整数,如果,则f≡g或者f(n)·g(n)≡1.
一直以来,许多唯一性的研究者对这一问题做了进一步的探讨,研究了条件减弱的情况下,对于整函数以及亚纯函数,是否保持结论成立,其中以仪洪勋和杨重骏所得定理较为简洁.
定理C[9]设f与g为两个非常数整函数,满足f′与g′以1为CM公共值,如果δ(0,f)+δ(0,g)>1,则f≡g或者f′·g′≡1.
定理D[10]设f与g为开平面上两个非常数亚纯函数,以∞为CM公共值,f(n)与g(n)以1为CM公共值,n为非负整数,如果δ(0,f)+δ(0,g)+(n+2)Θ(∞,f)>n+3,则f≡g或者f(n)·g(n)≡1.
我们自然想到:保持定理D的结论,分担1 CM和∞CM的条件是否可以减弱?2001年,Lahiri在他的论文[6]中引入了权分担的思想,2009年,徐洪焱,易才凤得到了一般性的结论(参见文[11]:
定理E[11]设f与g为非常数亚纯函数,f(n)与g(n)分担(1,0)(注:即以1为IM公共值),n为非负整数,那么
(1)如果f与g分担(∞,∞)(注:即以∞为CM公共值),且满足

(2)如果f与g分担(∞,0)(注:即以∞为IM公共值),且满足

利用这一思想我们得到下面定理:
定理1.1设f,g为开平面上两个非常数亚纯函数且分担∞IM,f(n)与g(n)分担1 IM,n为正整数,如果

则f≡g或者f(n)·g(n)≡1.
从上述定理,我们可以推出:
推论1.2设f,g为两个非常数整函数,f(n)与g(n)分担1 IM,n为正整数,如果

则f≡g或者f(n)·g(n)≡1.
事实上,从证明过程可以得出更精细的结论:
推论1.3设f,g为开平面上两个非常数亚纯函数且分担∞IM,f(n)与g(n)分担1 IM,n为正整数,如果
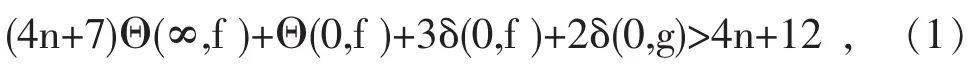
则f≡g或者f(n)·g(n)≡1.
推论1.4设f,g为两个非常数整函数,f(n)与g(n)分担1 IM,n为正整数,如果

则f≡g或者f(n)·g(n)≡1.
2 符号及引理
为了方便证明,我们将本文所用符号加以说明.我们分别用E和I表示线性测度有限和线性测度无穷的集合.记S(r,f)=o(T(r,f))(r→∞,r∉E).记k)(a,f)为f(z)-a的重级≤k的零点集合,重级零点只记一次.用表示在|z|≤r上f(z)-a的重级≤k的零点精简计数函数,重级零点只记一次表示在|z|≤r上f(z)-a的重级≥k的零点精简计数函数,重级零点只记一次.而.
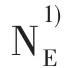
为了证明定理,我们将需要一些引理.
引理2.1[1](Milloux定理)设f为开平面上非常数亚纯函数,k为正整数,
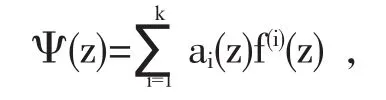
这里ai(z)(i=0,1,…,k)均为f(z)的小函数,则

及

引理2.2[4]设f为开平面上非常数亚纯函数,n为正整数,c为有限非零常数,则

引理2.3[5]设f为开平面上非常数亚纯函数,k为正整数,则
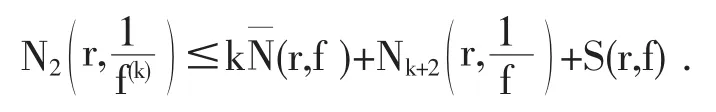
引理2.4[5]设f,g为开平面上两个非常数亚纯函数分担1 IM,则

引理2.5[6]设f,g为开平面上两个非常数亚纯函数且分担1 IM,若H≢0,则

引理2.6[5]设f,g为开平面上两个非常数亚纯函数且分担1 IM,如引理2.5所设H,若H≢0,则

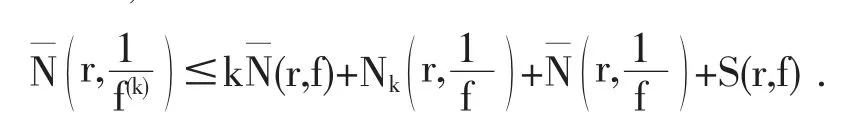
引理2.8设f,g为开平面上两个非常数亚纯函数且分担∞IM,f(n)与g(n)分担1 IM,n为正整数,如果δ(0,f)>0,δ(0,g)>0,则T(r,f)=O(T(r,g)),T(r,g)=O(T(r,f))。证明依据引理2.2

引理2.7[11]设f为开平面上非常数亚纯函数,k为正整数,则
即T(r,f)=O(T(r,g))。
同理可得T(r,g)=O(T(r,f))。
3 定理证明
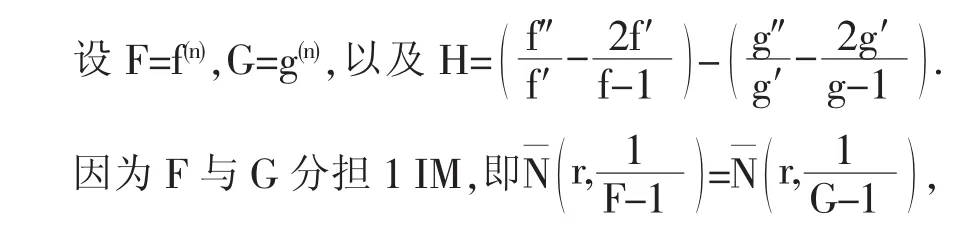
若H≢0,则应用引理2.4,引理2.5,引理2.6有


应用引理2.3即

而由(2)式以及引理2.2,有
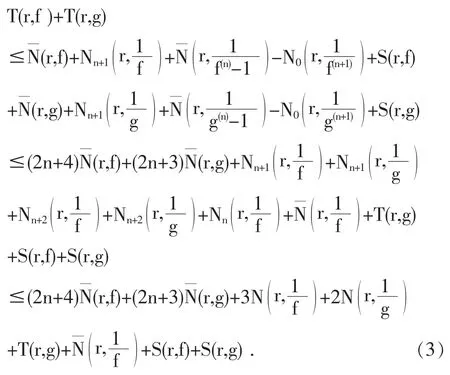
因为已知f,g分担∞IM,f(n)与g(n)分担1 IM,应用引理2.8,不妨设T(r,f)≥T(r,g),(3)式可以化为

于是
(4n+7)Θ(∞,f)+Θ(0,f)+3δ(0,f)+2δ(0,g)≤4n+12,
进而
(4n+7)Θ(∞,f)+4δ(0,f)+2δ(0,g)≤4n+12,
与已知(4n+7)Θ(∞,f)+4δ(0,f)+2δ(0,g)>4n+12矛盾,故H≡0,即
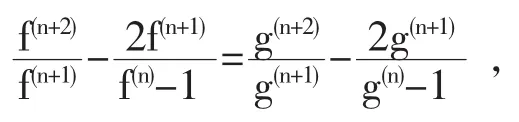
解此微分方程,得

其中a≠0,b是常数.下面分三种情况讨论H≡0.
情况1.b≠0,-1。
若a-b-1≠0,依据(4),有
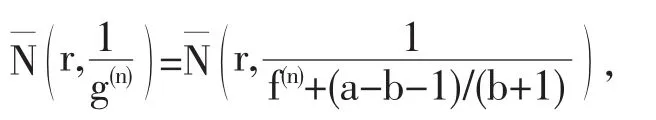
应用引理2.2,引理2.7以及f,g分担∞IM,可知
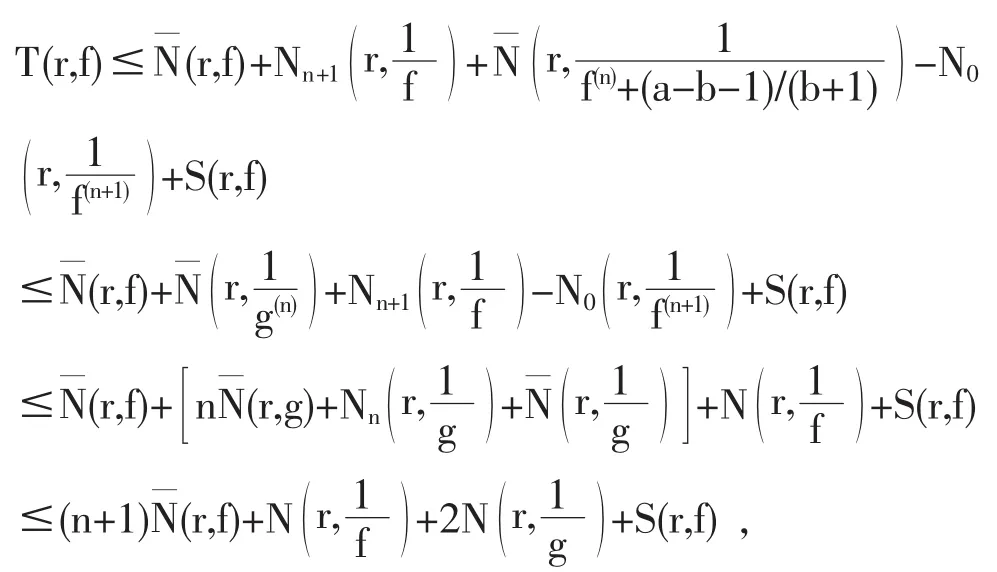
有(n+1)Θ(∞,f)+δ(0,f)+2δ(0,g)≤n+3,与已知(1)式矛盾.
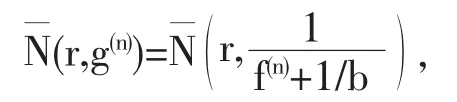
类似的可知

有2Θ(∞,f)+δ(0,f)≤2,与已知(1)式矛盾.


有(n+1)Θ(∞,f)+δ(0,f)+2δ(0,g)≤n+3,与已知(1)式矛盾.
若a=1,则f(n)≡g(n).设f(z)=g(z)+P(z),其中P(z)为次数小于n的多项式.由(1)可知,∞和0是f的亏值,进而f的下级μ>0,所以f必为超越函数[3],使得g也必为超越函数,显然T(r,f)=T(r,g)+S(r,f).
若P(z)≢0,则
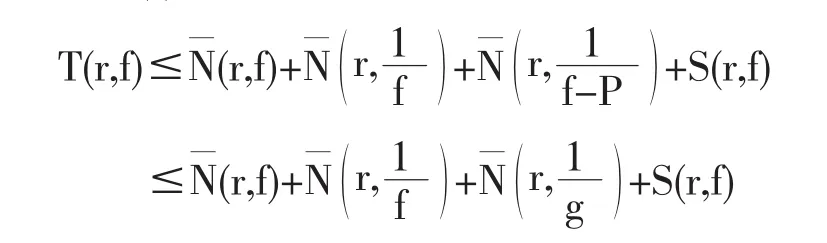
有Θ(∞,f)+δ(0,f)+δ(0,g)≤2,与已知(1)式矛盾.
所以必有P(z)≡0,故f≡g.

有2Θ(∞,f)+δ(0,f)≤2,与已知(1)式矛盾.若a+1=0,即a=-1,则f(n)·g(n)≡1.
定理1.1得证.
[1]Y i H.X.and Y ang C.C.:U niqueness Theory of M eromorphic Functions[M].(in Chinese)Science Press,Beijing,1995.
[2]杨乐.值分布论及其新研究[M].北京:科学出版社,1982.
[3]张广厚.整函数和亚纯函数理论——亏值、渐近值和奇异方向[M].北京:科学出版社,1986.
[4]H aymanW.K.:M eromorphicFunctions[M].O xford:Clarendon Press,1964.
[5]Banerjee A.:M eromorphic functions sharing one value [J].Int.J.M ath.M ath.Sci.,2005,22:3587-3598.
[6]LahiriI.:W eighted value sharing and uniqueness of meromorphic functions[J].Complex V ariables Theory A ppl.,2001,46(3):241-253.
[7]Y ang C.C.:O n tw o entirefunctions w hich together w ith their first derivatives have the same zeros[J].J. M ath.A nal.A ppl.,1976,56:1-6.
[8]Y i H.X.:A question of C.C.Y ang on the uniqueness of entire functions[J],K odai,M ath.J.,13(1990),39-46.
[9]仪洪勋,杨重骏.导数具有相同1-值点的亚纯函数的唯一性定理[J].数学学报,1991,(34):675-680.
[10]杨重骏,仪洪勋.具有亏值的亚纯函数的唯一性定理[J].数学学报,1994,(37):62-72.
[11]徐洪焱,易才凤.亚纯函数及其阶导数权分担两个值[J].纯粹数学与应用数学,2009,25,(4):777-785.
Meromorphic Functions with IM Sharing Two Values
XU Lin,NIU Hong-ling
(Department of Mathematics and Computer Science,Hebei Normal University for Nationalities, Chengde,Hebei 067000,China)
Researching into the meromorphic functions and the shared value of its n-th derivatives,this paper amends the theorems of H.X.Yi and C.C.Yang etc and obtains the following result:given:f and g are two non-constant meromorphic functions in the complex plane,plus f(n)and g(n)IM share 1(n is a positive integer).If(4n+7)Θ(∞,f)+4δ(0,f)+2δ(0,g)>4n+12,then either f(n)·g(n)≡1 or f≡g.
meromorphic functions;uniqueness;IM shared value
O13
A
2095-3763(2015)02-0074-04
2014-12-25
徐琳(1966-),女,江苏徐州人,河北民族师范学院数学与计算机系副教授,研究方向为函数论。

