基于行为博弈论的企业与其职工的互惠研究
张沛宇
(天津城市职业学院,天津300250)
基于行为博弈论的企业与其职工的互惠研究
张沛宇
(天津城市职业学院,天津300250)
以行为博弈论的序贯互惠模型为基础讨论企业与职工的博弈,考虑了在企业中工作的职工在工作的过程中会产生一个拖延,通过对企业与职工的序贯互惠均衡的讨论得出了可以解决问题的四个方向:增加未来收益预期、增加企业对职工的信任程度、增加企业给职工的每期收益、缩短工作的时间也就经常增加企业的新力量。而通过这样的互惠行为二者的收益都会增加。
行为博弈;序贯互惠均衡;拖延
现代企业中,存在着职工拖延的行为(尤其很多历史悠久的企业),因为职工拖延,企业生产效率下降。因而解决企业职工的拖延问题就很重要,否则企业将在竞争中被淘汰。很多企业解决问题的办法是强化管理,如李世明认为从职工收益、就业、岗位等几方面加强对职工的管理,可以减少职工的倦怠。[1]用博弈论的方法讨论企业与职工的问题时,传统博弈论假设:职工对于企业的贡献是时间的线性函数,根据子博弈完美性,二者的合作仅在最后一个阶段存在着背叛和不背叛的区别。行为博弈论认为在企业中工作的职工所得到效用并非仅仅是时间的线性函数,其中还包含着一个拖延的因子。企业和职工通过互惠可以适当改善二者之间紧张的关系,提高生产效率。
一、博弈要素
我们首先介绍博弈的三个核心要素。
1)局中人N={1,2},其中1代表企业,2代表在企业1工作的职工。
2)两个局中人采取的策略为s。
3)π1,π2为局中人1和局中人2的收益函数。下面我们着重讨论收益函数
博弈开始前企业有C的物质投入,w为局中人2获得的工资,我们假定在某一个时期M之内w是固定的。R是局中人1所获得的利润。时间节点k∈{1,2,…,M}。
黄湛冰认为:在企业和为其工作的管理者的博弈中,仅于奇数时间节点M处由局中人2决定是否背叛。[2]背叛和不背叛使得二者最后的收益有所不同。但实际情况是很多时候二者还要继续合作,只不过是局中人2会将其工作作一拖延,使得局中人1的收益下降,但不会减少得很多,此时局中人1不会轻易结束博弈(即终止与局中人2的劳动关系)。行为经济学家对于拖延的讨论很多,他们认为人们像局中人2对工作拖延的这种有限理性,董智勇认为有时候并不会给自己的收益带来损失,相反收益还可能会有所增加。[3]Labison给出了关于拖延的计算方法。[4]
因此我们假设:如果局中人2在工作过程中有拖延的行为时,其收益会有一个增加(可以认为他偷懒了,付出的工作成本降低了,因而收益增大了),同时局中人1会有一个相应的收益减少,于是二者的收益为:

其中δ为拖延的指数。β为贴现的系数。δ,β成为拖延因子。
拖延本质上是人们一种对现在的时间和将来的时间偏好的不一致。Labison认为人们很多时候都认为如果把现在应该完成的任务推到将来或许会有更多的收益。[4]也就是说从经济学角度而言,现在的时间和将来是不一样的,因而就造成了企业中一些职工长期以来的拖延。
如果局中人2在工作过程中没有拖延的行为时,二者的收益为:
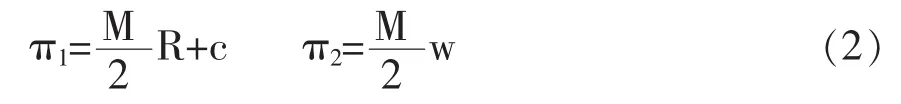
下面我们通过序贯互惠均衡来讨论企业与其职工的收益。我们仅从职工的决策考虑局中人收益的不同,因此企业的决策我们不予以考虑。
二、序贯互惠均衡
企业和职工的博弈的传统博弈论的纳什均衡,Fudenberg认为企业和职工都不合作,职工不努力工作,企业也会因生产效率低下压低职工工资,二者的收益都将变小,这是典型的囚徒的困境模型。[5]行为博弈论从互惠角度考虑二者的收益。下面我们先来看看Dufwenberg关于参与人之间的互惠的内容。[6]
(一)Dufwenberg模型中的主要定义
设N={1,2,…,n}为局中人集合,H为以前的策略集,Ai为局中人i的行为策略集。令A=∏i∈NAi,则就局中人的收益函数为πi:A→R,将πi称之为局中人的物质收益函数,但它并不是局中人所获得的唯一的收益函数。局中人所要最大化的效用里还有一项互惠收益。互惠收益依赖于局中人的信念。令Bij=Ai为局中人i对局中人j的可能策略的信念集,Cijk=Bij=Ak为局中人i对局中人j关于为局中人k的策略的信念的信念集。

类似地,参与人i所感知到的来自于参与人j的善意程度λij(bij,cijk)可表示为:

(二)企业和职工的收益函数
总效用:职工的总效用等于物质支付与互惠支付之和,而物质支付又可以拆成两部分,一个是当前的物质支付,另一个是职工对未来的预期所形成的收益,具体如下:

Yij是小于0的外生常数,表示的是局中人i对局中人j的互惠的敏感程度。
(三)序贯互惠均衡的存在定理
策略组合是一个序贯互惠均衡(SRE)是指;对2于所有的i满足

Dufwenberg证明了每个具有互惠激励因素的博弈中都存在着一个序贯互惠均衡。
三、均衡的条件分析
人具有普遍的互惠行为,对友善回报以友善(正互惠),对不友善回报概率以不友善(负互惠)。序贯互惠均衡告诉我们:如果存在一个序贯互惠均衡,局中人会通过改变自己的策略而增加收益,局中人1可以给局中人2更多的优惠,而局中人2也可以减少偷懒程度而使得局中人1收益增加。
p为职工诚实劳动时职工对企业对职工的信念的信念,也就是所说的局中人2对局中人1的态度取决于他认为其他局中人对他的态度,职工因为认为企业可能对他不好,而产生一个拖延导致生产效率低下。职工不诚实劳动时职工认为企业对职工的信念的概率为1-p,于是
职工如果选择诚实工作,则

职工如果诚实工作,其收益为:

职工如果拖延了,收益为:

U′≥U,即

其中Y2是局中人2对局中人1互惠的敏感程度,若(13)式成立,则在此达到序贯互惠均衡的要求,即局中人相互考虑对方的收益时,可以使各自的收益达到最大。通过对(13)式右侧的分析,可以得到以下的结论:
1)当其他量给定时,对于未来的收益μπ如果越大,就是增加未来收益预期,(13)式越容易满足。于是可以通过增加局中人2的预期的方式,如通过给局长人2提高加薪升职的期望,可以增加局中人1和局中人2的互惠。达到序列互惠均衡的要求。
2)当其他量给定时,p越大,就是企业对职工的信任程度越大,(13)式越容易满足,也就是说二者信任程度越高,越容易提高二者的收益。
3)当其他量给定时,w越大,就是企业付给职工的工资越高时,(13)式越容易满足,这就是为什么很多企业都愿意提高职工的待遇来激励职工努力工作的原因。
4)当其他量给定时,M越小,(13)越容易满足,就是职工工作的时间越短,越容易给人带来努力的印象,而越长就越显得偷懒。缩短工作的时间也就经常增加企业的新力量。
5)下面我们讨论拖延因子.Labison认为拖延因子δ,β都小于1。[4]
①当其他量给定时,β增加时,整个Y2会增加,也就是说当拖延的系数增加时,互惠敏感程度增大。因此系数β的变化不会从本质上影响局中人1和局中人2的互惠,即是说系数β对互惠敏感程度扰动较小。实际中,可以通过一些灵活的方法,如适当增加职工的文体活动,提高企业中的职工的积极性,减少拖延的程度。
②当其他量给定时,δ会直接影响Y2。Labison认为0<δ≤1,是一个人坚持时间一致性的偏好的程度。[4]δ=1表示的就是简单的指数贴现,当δ<1时,这些偏好表现了与时间的不一致性。从行为博弈论的角度而言,很多人做事愿意拖拖拉拉,在工作中就体现为一种拖延。久而久之,给个人和企业都带来了损失。所以调整δ可以改善Y2,就是让个人少拖延点,可以增加他对企业的好感,这个因子与其他的因子不同。是来自于局中人2个人的因素,比如企业增加对职工思想状态的调整,增加职工对工作和生活的信心。
③当Y2提高的时候,说明职工认为企业对他们是善意的,因而也会相应的降低拖延程度,增加工作产出。
四、结论
企业中职工的拖延的问题,对于企业和职工乃至整个社会都有现实的意义,一个企业如果可以通过采取适当的策略改善其与职工的关系,那么由此带来的收益提高是可以预测到的。很多文献对此做出了论述。本文从行为博弈论角度展开讨论,给出了二者因互惠而使得各自收益提高的结论:增加未来的收益,提高信任程度,缩短工作时间以及给职工增加升职加薪的机会,增加博弈双方的互惠,最终提高企业生产率。
[1]李世明.竞争消除某些国有企业怠工现象的根本措施[J].调查与思,2011,(4).
[2]黄湛冰,万迪昉.管理者时限问题的互惠解决方法[J].系统工程,2005,(9).
[3]董智勇.行为经济学[M].北京:北京大学出版社,2010.
[4]Laibson,D.L.Life-Cycle Consumption and H yperbolic D iscount Functions[J].European Economic Review,V ol, 2002,42,:861-871.
[5]黄涛译.博弈论[M].北京:中国人民大学出版社,2011.
[6]D ufw enberg,M artin&K irchsteiger,G eorg.A Theoryof Sequential Reciprocity[J].G ames and Economic Behavior,2004,(47):268-298.
On Reciprocity Between Enterprise and Its Employees Based on Theory of Behavioral Game
ZHANG Pei-yu
(Tianjin City Vocational College,Tianjin 300250,China)
This paper discusses the game between the enterprise and it's employees based on the model of sequential reciprocity with the employees'delay in the course of work considered and puts forward four ways to solve the problem and realize mutual benefit:to increase benefit expectation,terminal earnings,and degree of trust,and to decrease the working time,
behavioral game;sequential reciprocity;delay
O151
A
2095-3763(2015)02-0113-03
2014-12-20
张沛宇(1979-),男,河北唐山人,天津城市职业学院基础部讲师。

