核电厂安全壳极限抗压承载力及影响因素分析

宋辰宁，侯钢领，周国良

（1.哈尔滨工程大学哈尔滨150001；2.机械工业第六设计研究院有限公司，郑州450007；3.环境保护部核与辐射安全中心，北京100082）

核电厂安全壳是核岛最后一道安全屏障，它对维持核电厂正常运行，确保人员安全至关重要。在核电事故条件下，核安全壳将承受一定的内压，并要求保障其密封性。因此，核安全壳的极限抗压承载能力是国内外研究的重点。

根据研究方法来看，核电厂安全壳研究主要体现在试验研究、数值模拟和两者的结合。在结构试验方面：德国学者T.F.Kanzleiter等对1∶64安全壳模型进行了LOCA（丧失冷却剂事故）情况下的实验分析和理论推导，两者吻合良好［1］。美国Sandia国家实验室分别对1∶6和1∶4的安全壳模型进行承压实验，检验安全壳结构抵抗内部抗压的性能，得到在高压作用下的结构相关响应［2］。我国中冶集团赵树明等对秦山核电二期安全壳进行了整体性试验，研究了在内部表面压力0.35MPa、145℃汽水混合物极端情况下，安全壳的力学性能［3］。在数值模拟方面：清华大学陈勤等进行了内压荷载下安全壳1∶10模型结构非线性有限元分析，得到的极限内压为设计内压的3.35倍，验证安全壳结构的安全性［4］。台湾学者Hsuan-Teh Hu等考虑材料和结构的非线性，通过数值模拟给出了Mark III BWR堆型核电厂安全壳的极限承载能力［5］。中冶集团张会东等在考虑预应力损失的前提下，应用ANSYS软件，进行预应力混凝土安全壳结构的内压承载能力计算［6］。针对第三代核电机组AP1000，上海核工程研究设计院柳胜华等应用ANSYS软件，建立了钢安全壳的二维轴对称有限元模型，对设计内压下钢安全壳的结构性能进行了分析，为钢安全壳的应力评定提供了可靠的依据［7］。在结构试验和数值模拟综合分析方面：日本学者Prinja N K等在NUPEC（The Nuclear Power Engineering Corporation）项目支持下，进行了安全壳1∶4承压破坏试验和数值模拟对比分析，两者结果吻合较好，同时也验证了ABAQUS软件在极限承载力数值模拟方面的高精度性［8］。

核电厂安全壳极限抗压承载力、影响因素及其规律是核电结构安全评估、事故处理和结构设计的关键问题。本文以某安全壳为例，采用损伤塑性模型模拟混凝土的力学性能，双线形应力-应变模型模拟钢衬里和预应力钢束的材料非线性，暂不考虑设备阀门洞口、高温热效应、土与结构相互作用等因素的影响，基于ABAQUS软件系统地分析了核安全壳极限抗压承载力，并给出了结构自重、预应力、钢衬里等因素的影响规律，对核安全壳极限承载能力分析、结构设计和安全评定等方面具有一定的参考价值。

1 安全壳模型

本文分析选用的某安全壳由底板、筒壁、穹顶、钢衬里、普通钢筋和预应力钢束等部分组成。筒壁内径37m，外径39m，壁厚1m，穹顶内径48m，壁厚0.8m，结构高度61.5m。为避免出现应力集中现象，穹顶与筒壁交界处采用半径为6.4m的圆弧作倒角处理。混凝土强度等级为C50，钢衬里采用Q235钢，预应力钢束采用29φ15.7，1 860MPa级，安全壳筒壁中有三层预应力钢束，从内到外第一层竖向钢束120根，两层环向钢束共109根，穹顶的预应力钢束分三层总计117根，三层钢束相互呈60°夹角，安全壳结构如图1所示［9］。

结合相应的安全壳设计规范［10］和文献［4］，以保障其使用功能为前提，本文采用安全壳结构达到如下状态之一，即认为结构失效：

（2）混凝土的最大拉应变达到10 000×10-6；

（3）钢衬里的最大拉应变达到3 000×10-6。

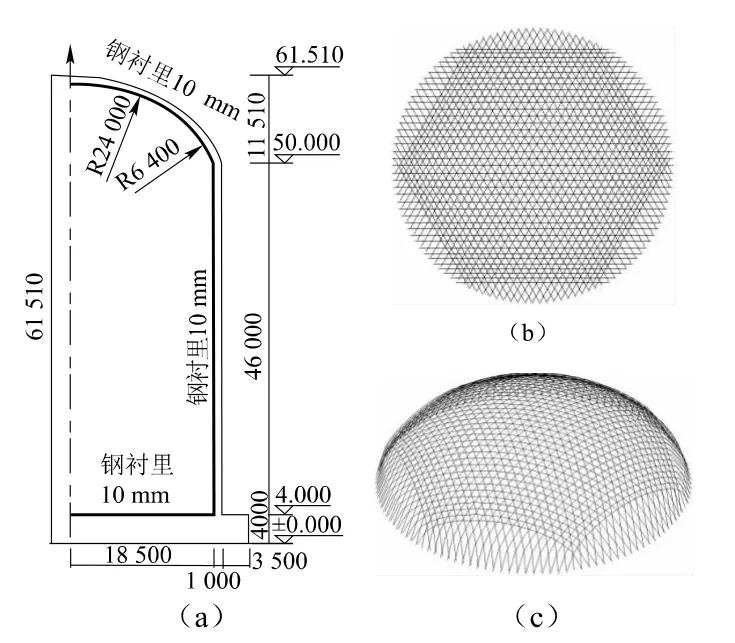
图1 安全壳结构图Fig.1 Structure of reactor containment

2 安全壳计算模型

2.1 有限元模型

根据安全壳和预应力钢束的对称性，本文选取结构的1／6作为计算模型，如图2所示，底部固定，两侧边界处施加对称约束。

图2 安全壳计算模型Fig.2 Calculation model of reactor containment

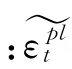
在部件的连接方面，混凝土内壁与钢衬里之间采用接触连接，预应力钢束与混凝土之间采用嵌入（embed）连接，运用降温法对预应力钢束施加预应力。

2.2 理论简化分析与数值模拟结果比较

为了验证数值模拟结果的准确性和了解结构性能，在暂不考虑普通钢筋、预应力钢束和钢衬里条件下，选择安全壳的横切面和纵切面进行承压分析［12］，计算模型如图3所示。理论解与ABAQUS数值模拟结果对比结果如表1、表2所示。从表中可以看出，理论解和数值解的最大误差小于12%，表明本文数值模拟结果比较可靠。

在关键帧提取器的粗识别阶段，已经筛选出大量的非目标区域，留下了少数候选区域。候选区域的图像特征点具有相似性，需要深度挖掘图像特征方可区分。因此，在关键帧提取器的精识别阶段，使用Alex-Net卷积神经网络模型，对候选目标区域提取深度卷积网络特征，生成特征向量，并利用关键帧提取器的SVM分类器将特征向量分类，得到最终的提取结果。

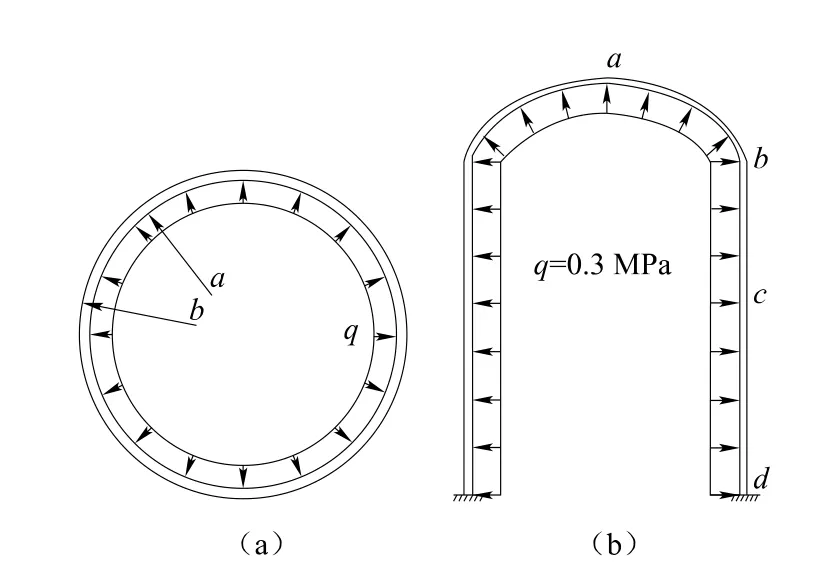
图3 理论解计算模型Fig.3 Calculation model of theoretical solution

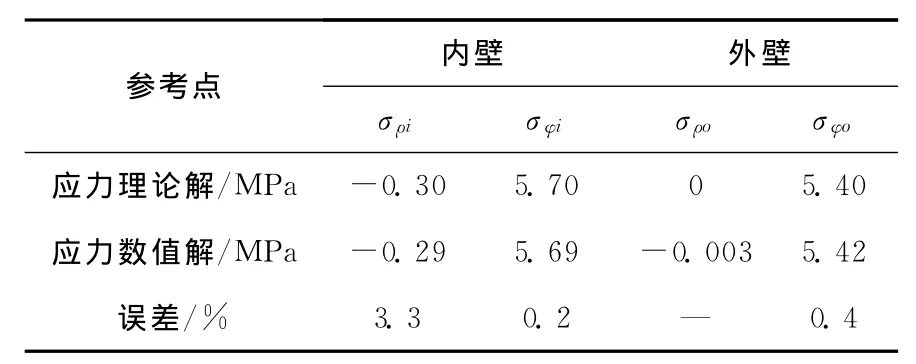
表1 横切面理论解、数值解及误差Table 1 Theoretical solution，numerical solution and error of cross sectionn

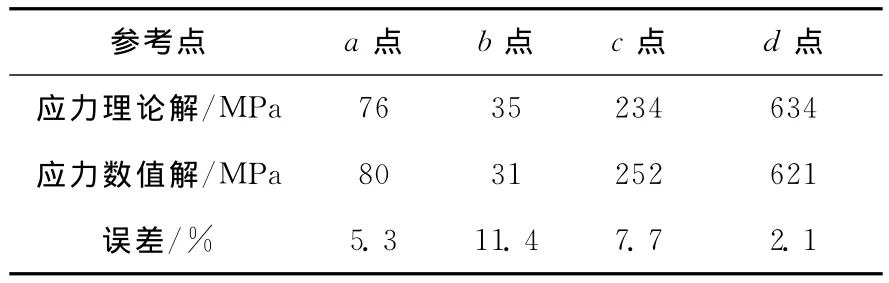
表2 纵切面理论解、数值解及误差Table 2 Theoretical solution，numerical solution and error of vertical section

3 极限承载能力及影响因素分析

本文首先对安全壳分三步加载，第一步：整体结构施加重力；第二步：施加预应力钢束预应力；第三步：安全壳内壁施加内压，进行极限承压分析。然后分别进行无自重、无预应力和无钢衬里情况下的承压分析，研究三种因素对安全壳极限承载力的影响情况。

3.1 核安全壳极限承压分析

3.1.1 整体结构

在自重和预应力荷载的基础上，不断增加内压，安全壳由受压状态逐渐向受拉过渡。当内压增大到0.70MPa时，安全壳变形情况见图4（a），从图中可以看出，安全壳基本恢复到未加载时的形状。随着内压的继续增大，筒壁和穹顶逐渐向外发生位移。当内压增大到1.02MPa时，达到极限状态，安全壳变形情况见图4（b）。此时，穹顶顶点向上位移为33.17mm，筒壁部分最大径向位移为24.51mm。

（a）0.70MPa内压变形图；（b）1.02MPa内压变形图

以筒壁部分半高处径向位移及穹顶顶点竖向位移为参考，位移随内压变化如图5、图6所示：

（1）在内压增大到0.70MPa左右时，筒壁部分半高处径向位移约为0，穹顶顶点竖向位移为1.30mm，内压基本上抵消了预应力钢束引起的变形；

（2）在内压增大到0.87MPa左右时，图中曲线的斜率都发生了突变，产生这种现象的原因是安全壳中的混凝土开始进入塑性；

（3）在1.02MPa内压作用下，筒壁半高处环向0°径向位移为22.58mm，环向30°径向位移为21.79mm，环向60°径向位移为20.51mm，三者之间的最大相差为9.2%。

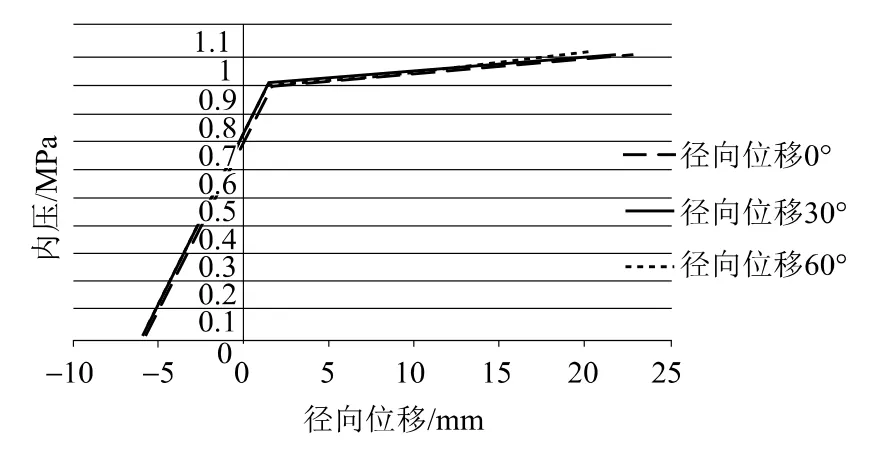
图5 筒壁半高处径向位移与内压关系曲线Fig.5 Curve between radial displacement and internal pressure at half height of cylinder wall

图6 顶点竖向位移与内压关系曲线Fig.6 Curve between vertical top displacement and internal pressure

3.1.2 混凝土部分

由于混凝土损伤塑性模型中没有裂纹的概念，采用“AC YIELD”参数来表示混凝土进入塑性后的情况。当内压增大到0.91MPa时，筒壁上部出现塑性区域并向下延伸，穹顶处部分混凝土进入塑性。当内压增大到0.93MPa时，塑性区域几乎布满整个筒壁。当内压增大到1.02MPa时，塑性区域布满安全壳的筒壁和穹顶。安全壳混凝土塑性区域发展与内压关系如图7、图8所示。

图7 不同内压作用下安全壳外壁塑性区域分布图Fig.7 Plastic regional distribution of reactor containment outer wall under different pressures

图8 不同内压作用下安全壳内壁塑性区域分布图Fig.8 Plastic regional distribution of reactor containment inner wall under different pressures

分析相关数据：

（1）对比安全壳外壁和内壁塑性区域的发展，可以看到，不管是穹顶部分还是筒壁部分，内壁塑性区域的扩展总是优先于外壁，在内压增大到1.02MPa时，内壁部分的混凝土几乎全部进入塑性状态，而外壁的仍有一部分混凝土处于弹性状态，这与理论分析中内壁先于外壁进入塑性的结论相吻合；

（2）随着内压的增大，筒壁环向30°上部、半高处和根部处混凝土依次进入塑性，与图7、图8中混凝土塑性区域的扩展相吻合，随着内压的增大，筒壁部分混凝土塑性区域从上部向根部扩展，如图9所示。

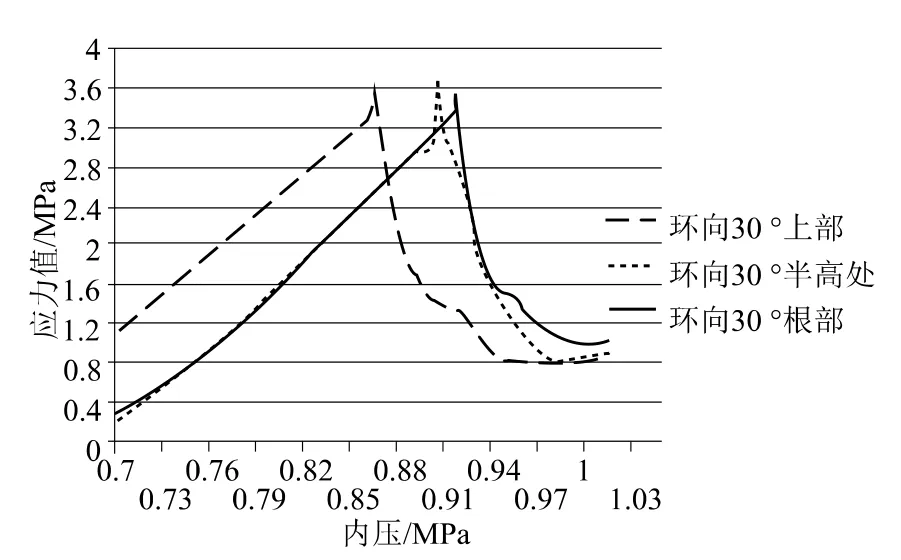
图9 筒壁环向30°处混凝土应力与内压关系曲线Fig.9 Curve between concrete stress and internal pressure at ring direction 30° of cylinder wall

3.1.3 预应力钢束

穹顶部分预应力钢束：当内压依次达到0.87MPa、0.89MPa、0.93MPa、0.95MPa时，穹顶顶部、仰角60°处、仰角45°处、仰角20°处的预应力钢束Mises应力依次大幅度增加，穹顶部分预应力钢束应力随内压变化关系如图10所示。

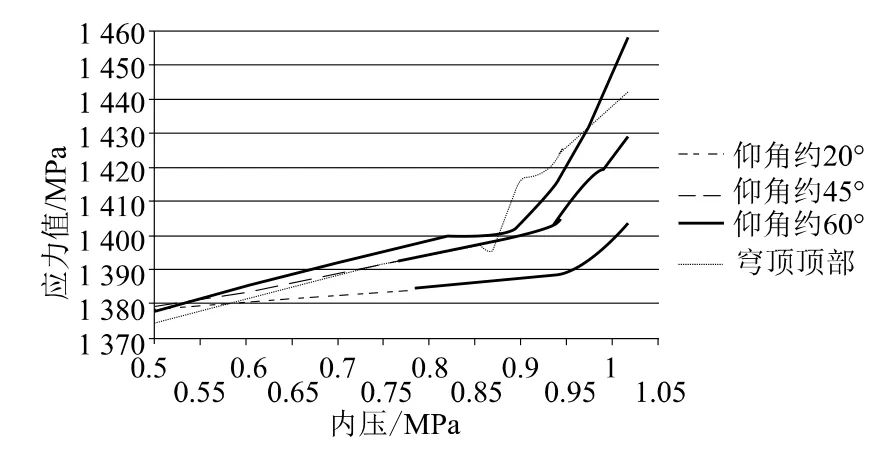
图10 穹顶部分预应力钢束应力与内压关系曲线Fig.10 Curve between prestressed tendons stress and internal pressure at dome

分析相关数据：

（1）在内压从0.87MPa增大到0.95MPa的过程中，穹顶顶部、仰角60°、45°、20°处混凝土依次进入塑性，引起预应力钢束的Mises应力发生突变；

（2）当内压增大到1.02MPa时，穹顶部分预应力钢束均处于弹性状态。

筒壁部分预应力钢束：当内压依次达到0.87MPa、0.91MPa、0.93MPa时，筒壁上部、半高处、根部的环向预应力钢束Mises应力依次大幅度增加，筒壁部分环向预应力钢束应力随内压变化关系如图11所示。当内压增大到0.87MPa时，筒壁环向3°、21°、39°、57°处的竖向预应力钢束Mises应力大幅度增加，筒壁部分竖向预应力钢束应力随内压变化关系如图12所示。

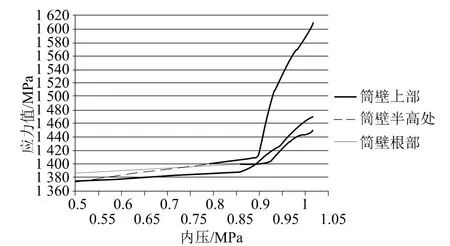
图11 筒壁环向预应力钢束应力与内压关系曲线Fig.11 Curve between prestressed tendons stress and internal pressure at ring direction of cylinder wall

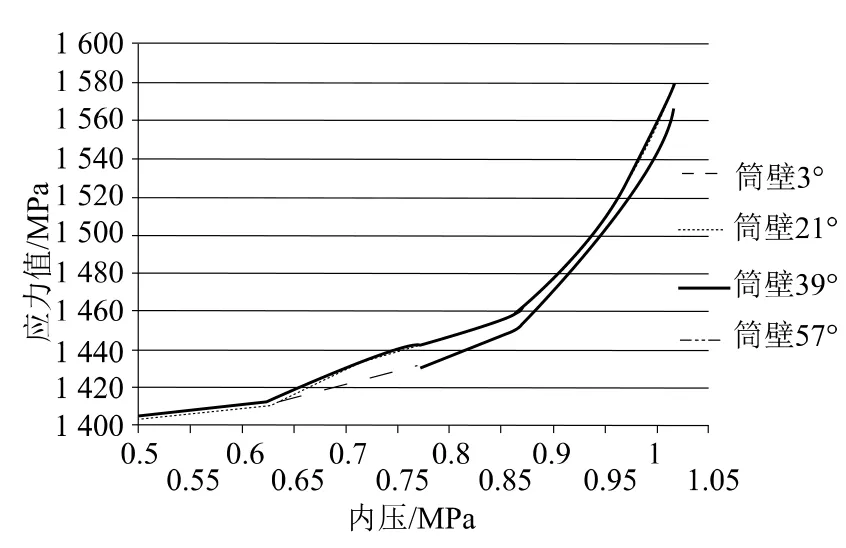
图12 筒壁竖向预应力钢束应力与内压关系曲线Fig.12 Curve between prestressed tendons stress and internal pressure at vertical direction of cylinder wall

分析相关数据：

（1）在内压从0.87MPa增大到0.93MPa的过程中，筒壁上部、半高处和根部混凝土依次进入塑性，引起环向预应力钢束的Mises应力发生突变；

（2）图12中四条曲线变化趋势一致，关于筒壁环向30°处母线对称的竖向预应力钢束（3°与57°，21°与39°）两两吻合良好，两组曲线之间差距不大，说明筒壁环向各角度处竖向预应力钢束应力变化情况基本一致；

（3）当内压增大到1.02MPa时，筒壁部分预应力钢束均处于弹性状态。

3.1.4 钢衬里

观察钢衬里的应力状态可以看出：当内压增大到0.87MPa时，筒壁环向30°半高处钢衬里的Mises应力大幅度增加；当内压增大到0.98MPa时，应力达到材料的屈服强度，之后随着内压的增大不再增长；当内压增大到1.02MPa时，筒壁几乎所有部分和穹顶上部钢衬里的Mises应力都达到了屈服强度。图13显示了1.02MPa内压作用下钢衬里的Mises应力和塑性区域分布图。

在1.02MPa内压作用下，混凝土中的最大拉应变为6 419×10-6，筒壁和穹顶大部分区域的拉应变为2 000×10-6～3 000×10-6，远远小于限值10 000×10-6；钢衬里中的最大拉应变出现在筒壁上部与穹顶交界处，为3 114×10-6，超过限值3 000×10-6，已经达到安全壳的极限状态，即可认为该安全壳的极限承载力为1.02MPa。

图13 p=1.02MPa时钢衬里模拟结果Fig.13 Simulation result of steel liner when internal pressure is up to 1.02 MPa

3.2 无自重、无预应力和无钢衬里模拟结果

无自重情况：不考虑结构自重，当内压增大到0.66MPa时，安全壳基本恢复到未加载时的形状。当内压增大到0.99MPa时，安全壳达到极限状态（钢衬里达到极限应变）。此时，穹顶顶点向上位移为46.47mm，筒壁部分最大径向位移为22.25mm。

无预应力情况：不考虑预应力，当内压增大到0.08MPa时，安全壳基本恢复到未加载时的形状。当内压增大到0.39MPa时，安全壳达到极限状态（钢衬里达到极限应变）。此时，穹顶顶点向上位移为65.95mm，筒壁部分最大径向位移为42.02mm。

无钢衬里情况：不考虑钢衬里，当内压增大到0.63MPa时，安全壳基本恢复到未加载时的形状。当内压增大到0.93MPa时，安全壳达到极限状态（预应力钢筋屈服）。此时，穹顶顶点向上位移为44.27mm，筒壁部分最大径向位移为22.97mm。

3.3 安全壳内压影响因素分析

表3中列出四种分析工况下安全壳恢复原形以及破坏时的内压值。结果表明：自重、预应力和钢衬里均对安全壳的承压分析有利。其中自重和钢衬里的影响较小，低于10%，预应力的影响较大，超过60%。

表4中列出四种分析工况下穹顶的竖向位移和筒壁径向位移，无自重或无钢衬里时，穹顶竖向位移增大约30%～40%，筒壁径向位移减少约5%～10%；无预应力时，穹顶竖向位移增大接近一倍，筒壁径向位移增大超过70%。

表3 自重、预应力和钢衬里对安全壳内压的影响Table 3 Influence of gravity，prestress and steel liner on internal pressure

从表3、表4中可以看出，预应力对安全壳极限承载力以及位移影响较大，自重和钢衬里影响相对较小。从表5中可以看出，在钢衬里存在的情况下，它控制着安全壳是否达到极限状态，无钢衬里时，预应力钢筋起控制作用。因此预应力钢束和钢衬里是安全壳极限承载力分析的决定性因素，也是实际工程中的关键指标。

表4 自重、预应力和钢衬里对安全壳位移的影响Table 4 Influence of gravity，prestress and steel liner on displacement

4 结论

本文应用有限元软件ABAQUS，采用损伤塑性模型模拟混凝土的力学性能，双线形应力-应变模型模拟钢衬里和预应力钢束的材料非线性，对某安全壳进行极限抗压承载力分析，并给出结构自重、预应力和钢衬里对极限内压和破坏形式的影响和影响规律。主要结论如下：

（1）系统给出在不同压力状态下结构响应。即有：当内压增大到设计内压0.35MPa时，安全壳中的混凝土、预应力钢束、钢衬里均处于弹性状态，满足正常使用要求。当内压增大到0.87MPa时，安全壳筒壁上部混凝土开始进入塑性，并引起结构内力重分布，导致混凝土、预应力钢束和钢衬里中应力值大幅度增加。在内压从0.87MPa增大到1.02MPa的过程中，筒壁混凝土的塑性区域从上部向根部扩展，穹顶混凝土的塑性区域从顶部向与筒壁交界处扩展，筒壁混凝土优先于穹顶混凝土进入塑性，在此过程中，钢衬里逐渐进入塑性状态。当内压增大到1.02MPa时，钢衬里中最大应变超过限值3 000×10-6，安全壳达到极限状态，此时预应力钢束尚未屈服。安全壳穹顶顶点向上位移为33.17mm，筒壁部分最大径向位移为24.51mm。

（2）通过数值模拟，得到该预应力混凝土安全壳的极限承载能力为1.02MPa，为设计内压0.35MPa的2.91倍，达到了国际安全裕度≥2.5的要求。在各种影响因素中，预应力钢束和钢衬里对安全壳的极限承载力和破坏形式起着重要作用，在安全壳设计时，要重点关注这两部分构件。

5 致谢

本文得到哈尔滨工程大学中央高校基本科研业务费专项资金项目：核安全壳振动台试验数值模拟研究（HEUCFZ1127）的资助，在此表示衷心的感谢。

［1］ T.F.Kanzleiter.Experimental investigations of pressure and temperature loads on a containment after a loss-ofcoolant accident［J］.Nuclear Engineering and Design，1976，159-167.

［2］ P.Anderson.Analytic study of the steel liner near the equipment hatch in a 1：4scale containment model［J］.Nuclear Engineering and Design，2008，1641-1650.

［3］ 赵树明，林松涛，王永焕.秦山核电二期安全壳结构整体性试验［J］.工业建筑，2003，33（9）：38-43.

［4］ 陈勤，钱稼茹.内压荷载下安全壳1∶10模型结构非线性有限元分析［J］.工程力学，2002，19（6）：73-77.

［5］ Hsuan-Teh Hu，Jiin-Iuan Liang.Ultimate analysis of BWR Mark III reinforced concrete containment subjected to internal pressure［J］.Nuclear Engineering and Design，2000，195：1-11.

［6］ 张会东，林松涛，王永焕.核电厂安全壳结构的内压承载能力计算分析［J］.工业建筑，2007，37（8）43-46.

［7］ 柳胜华，葛鸿辉.钢安全壳在设计内压下的轴对称有限元分析［J］.第16届全国反应堆结构力学会议论文集，2010：654-658.

［8］ Prinja N K，Shepherd D.Theory and Practice，Professional Engineering Publishing［M］.London：Institute of Mechanics Engineers，2003.

［9］ 刘立.某核安全壳振动台试验数值模拟研究［D］哈尔滨工程大学硕士学位论文，2009.

［10］ ACI Standard 359-04.Code for concrete containment.

［11］ Abaqus／CAE User's Manual.

［12］ 徐芝纶.弹性力学［M］.北京：高等教育出版社，2006：63-67.