全空间中Kirchhoff型方程正确的存在性

殷国帅，张福伟，刘进生，郭祖记

（太原理工大学 数学学院，山西 太原030024）

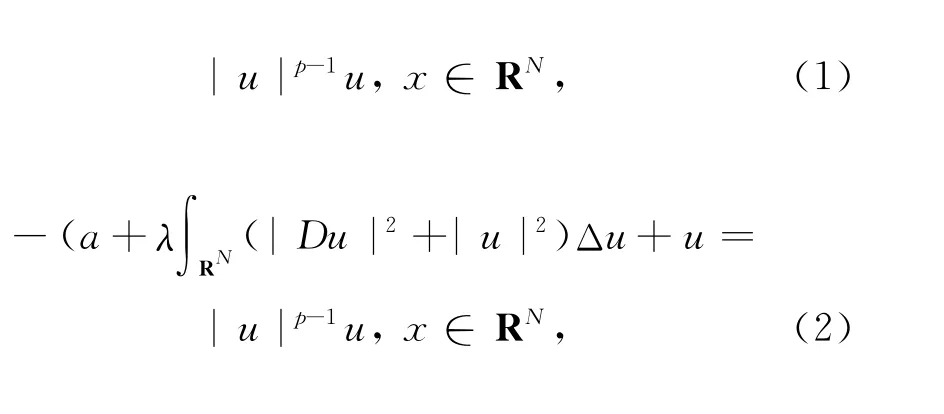
0 引言与主要结果

考虑以下三类Kirchhoff型方程

和

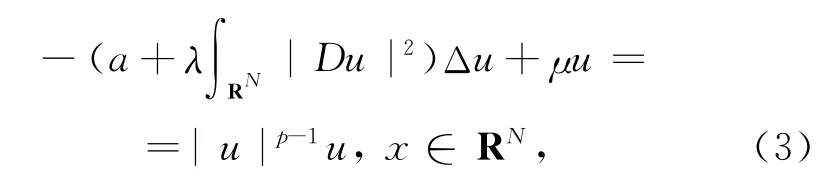
正确的存在性.其中空间维数N≥2，参数λ＞0，常数a＞0，μ＞1，1＜p＜2＊-1，当N=2时，2＊=∞，当N≥3时

本文记U是方程-Δu+u=|u|p-1u，x∈RN的唯一正径向解［1-4］.关于方程（1）～（3），得到了如下三个结果.定理1 1）当N=2，3且1＜p＜3时，或者当N≥4且1＜p＜2＊-1时，记

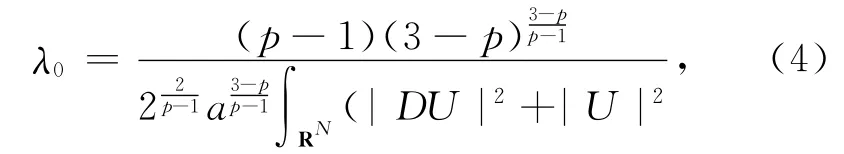
则当λ∈（0，λ0）时，方程（1）有两个正解；当λ=λ0时，方程（1）有一个正解；当λ∈（λ0，+∞）时，方程（1）无非平凡解.

2）当N=2，3且p=3时，记

则当λ∈（0，λ1）时，方程（1）有一个正解；当λ∈［λ1，+∞）时，方程（1）无非平凡解.

3）当N=2，3且3＜p＜2＊-1时，方程（1）有一个正解.

定理2 1）当N=2时，记

则当λ∈（0，λ0）时，方程（2）有一个正解；当λ∈［λ0，+∞）时，方程（2）无非平凡解.

2）当N≥3时，记

则当λ∈（0，λ1）时，方程（2）有两个正解；当λ=λ1时，方程（2）有一个正解；当λ∈（λ1，+∞）时，方程（2）无非平凡解.

定理3 1）当N=2，3时，对于任意的λ＞0，方程（3）有一个正解.

2）当N=4时，记

则当λ∈（0，λ0）时，方程（3）有一个正解；当λ∈［λ0，+∞）时，方程（3）无非平均解.

3）当N≥5时，记

则当λ∈（0，λ1）时，方程（3）有两个正解；当λ=λ1时，方程（3）有一个正解；当λ∈（λ1，+∞）时，方程（3）无非平凡解.

同时，也得到了与上面三个方程相关的临界或超临界Kirchhoff型方程非平凡解的不存在性结果.

定理4 如果N≥3，p≥2＊-1，常数a，b＞0，则Kirchhoff型方程

只有零解.

定理5 如果N≥3，p≥2＊-1，常数a，b＞ 0，则Kirchhoff型方程

只有零解.

定理6 如果N≥3，p≥2＊-1，常数a，b， μ＞0，则Kirchhoff型方程

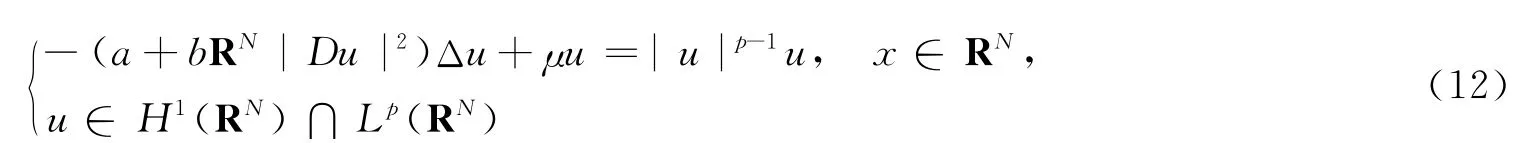
只有零解.

近年来，一些学者研究了Kirchhoff型方程

式中：常数a，b＞0，λ≥0.例如，在文献［5］中，李等考察了方程（13）在b=1，V（x）=1，N≥3时的正解的存在性.假设f∈C（R+，R+）满足次临界增长条件并且是超线性的，他们证明了存在λ0＞0，当λ∈［0，λ0）时，方程（13）至少存在一个解.然而，当λ≥λ0时，方程（13）仍然是一个待解决的问题.在文献［6］中，李等考察了方程（13）在f（u）=|u|p-1u及N=3时的非平凡解的存在性.假设1＜p≤2和V（x）满足.

（V1）对于几乎处处地x∈R3，有成立，并且上述不等式在一个正的Lebesgue测度上成立；

（V2）存在＞0使得

或者V（x）恒等于正常数.他们证明了存在λ1＞0，当λ≥λ1时，方程（13）没有非平凡解.受到上述文章的启发，本文在定理1中讨论当b=1，V（x）=1，f（u）=|u|p-1u及N≥2时方程（13）正解的存在性.由于本文的方法可以考虑到λ的所有情形，因此，所得结果可以看成是文献［5-6］的部分推广.

有界区域上的Kirchhoff型问题

已经被众多学者所研究，例如文献［7-8］等，其中常数a，b＞0，Ω＜RN.他们给出了许多关于问题（14）的可解性条件.也有人研究更一般的Kirchhoff型问题非平凡解的存在性，其中M是一个给定的连续函数，如文献［9-10］等.在上述问题中，当M（s）=a+λs，f（x，u）=|u|p-1u-u，Ω=RN时，问题（15）就变成了问题（2）.

还有学者研究方程

式中：常数a，b＞0，V（x）∈C（RN，R）.一些有趣的结果可以参见［6，11-12］.在文献［6］中，李等还得出了当f（x，u）=|u|p-1u，N=3，2＜p＜5且V（x）是正常数时方程（16）存在一个正的基态解.本文在方程（3）中研究了f（x，u）=|u|p-1u和V（x）是正常数的情形.对于N≥2时，讨论了当b的不同取值时方程（16）的解的性态.

对于临界指数方程，李等在文献［13］中也得到了当N=3，V（x）=1，f（x，u）=u5时，方程（16）无非平凡解的结论.关于此，本文也得到了一系列的结论.

已有的相关文献的证明方法不同，本文构造了一系列的函数变换，通过它们可将Kirchhoff型方程化为椭圆型方程，进而利用椭圆型方程的已有结果，得到Kirchhoff型方程的可解性结论.同时，本文的证明方法也表明，尽管Kirchhoff型方程是非局部方程，但它与局部的椭圆型方程却有着十分密切的内在联系.

1 主要结果的证明

下面应用函数变换法给出本文主要结论的证明.

定理1的证明

因此，v=U.所以，得到代数方程

因此，方程（1）与方程（19）有同样多的解.

2）当N=2，3且p=3时，通过解线性方程（19）可知当λ∈（0，λ1）时，方程（19）有一个正解当λ∈［λ1，+∞）时，方程（19）无正解，其中λ1由式（5）给出.

3）当N=2，3且3＜p＜2＊-1时，考虑幂

最后，由方程（1）与方程（19）有同样多的解即得结论.

定理2的证明

令ε=λA，则式（21）等价于

因此，方程（2）与方程（22）有同样多的解.

1）当N=2时，通过解线性方程（22）知，当λ∈（0，λ0）时，方程（22）有一个正解ε=λ（1-当λ∈［λ0，+∞）时，方程（22）无正解，其中λ0由式（22）给出.

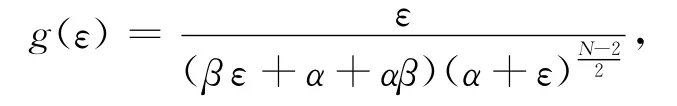
由于

所以，当0＜ε＜ε1时，当ε1＜ε＜+∞时，并 且g（0）=0，知函数λ=g（ε）的图像先增后减，且在ε1处取得最大值.因此可以得到当λ∈（0，λ1）时，方程（22）有两个正解；当λ=λ1时，方程（22）有一个正解；当λ∈（λ1，+∞）时，方程（22）无正解，其中λ1由式（7）给出.

最后，由方程（2）与方程（22）有同样多的解即得结论.

定理3的证明

1）当N=2时，对于任意的λ＞0，方程（24）存在唯一正解当N=3时，对于任意的λ＞0，由次线性函数及线性函数增减性易知方程（24）存在唯一正解.

2）当N=4时，通过解线性方程（24）可知，当λ∈（0，λ0）时，方程（24）有一个正解A=当λ∈［λ0，+∞）时，方程（24）无正解，其中λ0由式（8）给出.

当λ∈（λ1，+∞）时，方程（24）无正解.

最后，由方程（3）与方程（24）有同样多的解即得结论.

定理4的证明

定理5，定理6的证明与定理4的证明类似，略.

［1］Willem M.Minimax theorems，progress in nonlinear differential equations and their applications［M］.Boston：Birkhäuser Boston，Inc.，1996.

［2］Gidas B，Ni W M，Nirenberg L.Symmetry and related properties via the maximum principle［J］.Comm.Math.Phys.，1979（68）：209-243.

［3］Kwong M K.Uniqueness of positive solution ofΔuu+up=0［J］.Archive Rat.Mech.Anal.，1989（105）：243-266.

［4］Strauess W A.Existence of solitory waves in higher dimentions［J］.Comm.Math.Phys.，1977（55）：149-162.

［5］Li Y H，Li F Y，Shi J P.Existence of a positive solution oto Kirchhoff type problems without compactness conditions［J］.J.Differential Equations，2012（253）：2285-2294.

［6］Li G，Ye H.Existence of positive ground state solutions for the nonlinear Kirchhoff type equations in R3［J］.J.Differential Equations，2014（257）：566-600.

［7］Cheng B T.New existence and multiplicity of nontrivial solutions for nonlocal elliptic Kirchhoff type problems［J］.J.Math.Anal.Appl，2012（394）：488-495.［8］Liang Z P，Li F Y，Shi J P.Positive solutions to Kirchhoff type equations with nonlinearity having prescribed asymptotic behavior［J］.Ann.I.H.Poincaré-AN，2014，31（1）：155-167.

［9］Alves C O，Correa F J S A，Figueiredo G M.On a class of nonlocal elliptic problems with critical growth［J］.Differ Equ.Appl.，2010（2）：409-417.

［10］Ma T F.Remarks on an elliptic equation of Kirchhoff type［J］.Nonlinear Analysis，2005（63）：e1967-e1977.

［11］He X M，Zou W M.Existence and concentration behavior of positive solutions for a Kirchhoff equation in R3［J］.J.Differential Equations，2012（252）：1813-1834.的

［12］Jin J H，Wu X.Infinitely many radial solutions for Kirchhoff-type problems in RN［J］.J.Math.Anal.Appl.，2001（369）：564-574.

［13］Li G，Ye H.Existence of positive solutions for non-linear Kirchhoff type problems in R3with critical Sobolev exponent［J］.Math.Meth.Appl.Sci.，2013：3000.