求解固体力学反问题的广义边界控制方法

王明清，刘桂荣

（1.浪潮集团高效能服务器和存储技术国家重点实验室，山东 济南250101；2.太原理工大学 应用力学与生物医学工程研究所，山西 太原030024；

3.美国辛辛那提大学 航空航天学院，美国 俄亥俄州45221）

0 引 言

对于固体力学而言，通常需要控制方程以及所有边上的边界条件，进而求出问题域位移，应力以及应变等未知量.一般来说，只要物理问题是适定的，那么问题的解是存在且唯一的.然而，在实际的工程应用以及科学研究中，很大一部分问题是不具有这种适定性的［1］.对于上述固体力学问题，当所有边界上的信息都已知，其适定性才可得到保障.但有些情况下，边界条件是不可测的［1］.例如，在悬臂梁模型中，固定端位移的测量是困难的，同时自由端位移及应力的测量是比较容易的.因此，常规求解正问题的方法是不能得到稳定精确的数值解的.在同一边界上同时给出了两类边界条件，这是一类典型的柯西问题.这类柯西反问题是不适定的，即测量数据微小的扰动将导致结果产生巨大误差［1］.Lars Eldén［2］等人已经给出了关于椭圆型偏微分方程柯西问题的稳定性分析.其他微分方程的柯西问题可参见文献［3-8］.

基于有限元方法求解柯西反问题的精确有效且稳定的数值方法，首次引入了广义边界控制的思想，将问题域未知边界上位移的求解转化成求解包含一组参数化后未知系数的线性代数方程组的直接方法，不同于其他方法，无需多次迭代，格式更加简洁.Tikhonov正则化有效地克服了随机扰动带来的不适定性.

本文介绍了固体力学柯西反问题，提出了有限元方法求解固体力学反问题的广义边界控制格式，并给出数值例子，验证了算法的有效性和稳定性.

1 问题的提出

1.1 正问题

如图1所示的二维悬臂梁，其区域为Ω，边界为Γ，其中Γ1∪Γ2∪Γ3∪Γ4=Γ且Γi∩Γj=φ，（i≠j）.悬臂梁材料为各向同性的弹性材料，施加在悬臂梁右边界Γ4上的牵引力记为fb=［fx，fy］T，而在其余的边界上没有牵引力.其中，fx为x方向上的力，fy为y方向上的力.Γ1上的位移是给定的，可以记为UΓ1=［uΓ1，vΓ1］T.

相容方程为

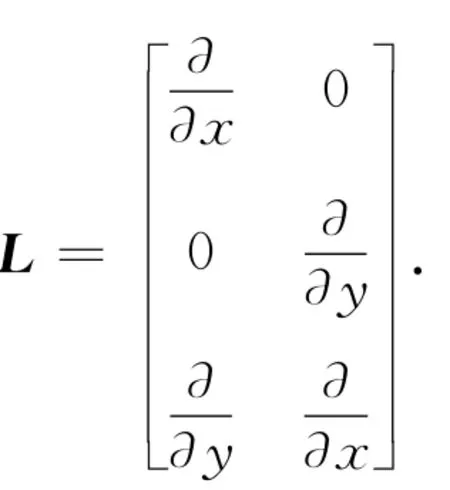
本构方程（胡克定律）为

正问题的控制方程可由动力学平衡方程给出，其矩阵格式表述为

其边界条件为

图1 右端施加牵引力的悬臂梁模型 Fig.1 A cantilever beam subjected to a traction on the right edge

1.2 柯西反问题

悬臂梁结构是工程系统中最常用的部件之一.然而，直接表述其左边界Γ1上的位移通常是非常困难的，多数情况下以UΓ1=0.因此，可得到前面定义的过于理想化的数学正问题.这种过度的简化往往会造成应力分析中巨大误差.为了使应力分析更加精确，不得不测量出边界Γ1的实际位移，使正问题具有更加可靠的解.但直接测量出边界Γ1上的位移通常是比较困难的，而测量边界Γ4是非常方便的.换言之，Γ1上不给任何条件，Γ4上既给出Dirichlet边界条件又给出Neumann边界条件，这是一个柯西反问题

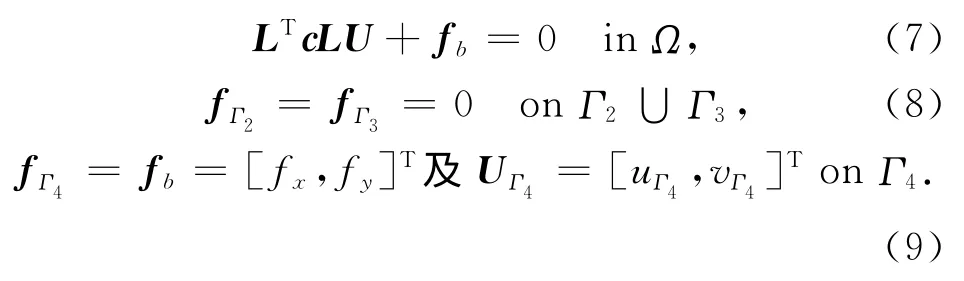
这类柯西问题是不适定的9：测量数据微小的扰动将导致结果产生巨大误差.

2 基于有限元方法的广义边界控制

鉴于有限元方法是求解弹性悬臂梁正问题（3）～（6）有效的方法，本文求解反问题的过程是基于有限元方法提出的.

首先将问题域离散成一组单元与节点，然后构造形函数，通过Galerkin弱形式构造单元刚度矩阵，组装整体刚度矩阵，最后施加边界条件，得到以下有限元方程

式中：K为整体刚度矩阵；U以及F分别为Ω∪Γ上所有节点的位移向量及节点力向量.

将Γ1上所有的节点从1到l编号，其它节点编号为l+1到n.重新排列矩阵或向量中的元素，等式（10）写成分块形式如下

式中：I为单位矩阵；矩阵O的所有元素都为零，并且

式中：ui和vi分别为水平方向及竖直方向的节点位移；l为边界Γ1上的节点数目；（n-l）为悬臂梁有限元模型其它部分的节点数目.

通过边界条件（4），可得F1=U1.对于等式（7）～（9）定义的反问题，边界Γ1上的节点位移UΓ1是未知的.首先将边界Γ1上的条件参数化：

式中：φi（x）是基函数，这里选取多项式为基函数.等式（11）中的F1可以表示为

c

i及di（i=1，2，…，k）为需要求解的系数，总共有2k个未知量.

施加边界条件后的整体刚度矩阵K是可逆的，将K-1记为

令B1=［I，-P-1Q］T，B2=［O，P-1］T，由式（10），（14）可知，

在式（15）中，B1，B2及F2是已知的，但F1是未知的.由式（12）和（13）可知，可表示为

将式（16）代入式（15）可得

为简化描述，标记N=B1M以及η=B2F2.式（17）可重新写为

在式（15）中，节点位移向量U是未知的.但边界Γ4上的节点位移向量是已知的，经过适当的排序后可以写成：

抽取等式（18）中矩阵N以及向量η中与边界Γ4上节点编号一致的行，形成新的矩阵和向量分别为

边界Γ4上的位移可以表示为

3 正则化方法

由于反问题的不适定性，直接运用传统的高斯消去法或最小二乘法求解等式（20）是十分不稳定的［10］，需要将不适定的问题正则化.

Tikhonov和Arsen（1986）提出的Tikhonov正则化便是最常用的方法之一.这种简洁的非迭代方法可求得到柯西反问题的稳定解.另外一种有效的方法是奇异值分解方法（SVD）［11］，然而对于大型问题SVD方法往往需要很大的花费［10］.

本文将采用Tikhonov正则化方法.线性代数方程组（20）的Tikhonov正则化解为

其中，fσ表示Tikhonov泛函，定义为

其中，‖·‖代表欧几里得范数且σ为正则化参数.

为得到Tikhonov正则化解Θσ，需要求出▽fσ（Θ）=0.等式（21）的解便是正则化方程的解：

当σ=0时，便是常见的最小二乘解或高斯消元所得到的解，这样的解往往是不稳定的.通过增加一个正则化参数σ，可以将范数‖Θ‖控制在一个合理的范围内.

正则化参数σ的选取仍然是一个重要的研究课题.目前，有两个比较常用的选取方法，即GCV方法以及L曲线法.在本文的讨论中主要采用L曲线法，基于一种无扰动准则确定一个合适的σ值.Hansen和O'Leary［12-13］是最早应用L曲线法研究不同参数对于正则化系统的影响，L曲线法选取正则化参数的过程可以概括为：

定义一条曲线

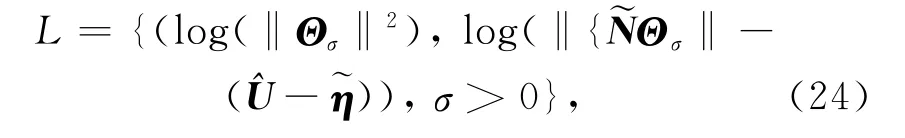
这条曲线被称为L曲线，合适的正则化参数σ往往是曲线“拐角”处的点所对应的值.

本文应用了Hansen［14］提供的Matlab代码求解离散的不适定方程组（20）.将L曲线法选取的正则化参数记为σ＊，方程组（20）的正则化解记为Θσ＊.将Θσ＊代入等式（16）可得

最终反问题（7）～（9）转化成了正问题（3）～（6）.其解为

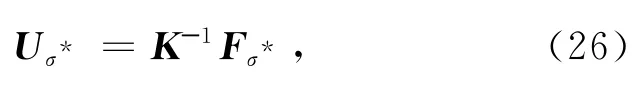
4 数值验证

为直观验证算法的有效性以及稳定性，定义相对均方根误差为

为简化讨论，考虑问题域Ω=｛（x，y）∶0≤x≤L，-5≤y≤5｝，其中L为给定常数.如图2所示，称边界Γ1的两个端点分别为“up”以及“lo”节点.

图2 悬臂梁模型问题域 Fig.2 The solution domain of the problem

例 假设材料的杨氏模量为E=3×107且泊松比为ν=0.3，施加在右边界Γ4上的牵引力为fb=［0，1 000］T.为了得到问题的参考解，分别给出“up”节点以及“lo”节点处的位移Uup=［0，-1×10-5］T及Ulo=［0，-8×10-2］T.其余边界上（Γ／Γ4）的应力设为0.在这种情况下，此问题为典型的正问题.因此，可以用有限元方法求出问题域内任意节点的位移U，也包括边界Γ4.考虑与以上正问题所对应的反问题，可将边界Γ4上的位移UΓ4作为反问题中的已知条件，并且节点位移Uup与Ulo均已知.运用本文第2节中提出的广义边界控制及Tikhonov正则化方法求出数值解U＊.

4.1 正则化的有效性验证

为使测试结果更具说服力，假定固体力学模型的长度为L=20，且对边界Γ4上的位移施加δ=5%的随机扰动.

测试结果如预期，运用最小二乘法等非正则化的方法（令等式（23）中的σ=0）求解带扰动的线性方程组是非常不稳定的，结果可参见图3.图3中实线代表有限元方法得到的参考解，点线为最小二乘解.显然，最小二乘法求解不适定问题是十分不稳定的.高斯消去法等类似的非正则化方法会得出相同的结论.

图4展示了运用Tikhonov正则化且通过L曲线法选取正则化参数σ后所得到的反问题的解.与最小二乘法等非正则化方法相比，Tikhonov正则化结果极好地吻合了参考解.因此，可断定Tikhonov正则化克服柯西反问题不适定性的有效方法.同时，L曲线法为Tikhonov正则化选取了一个合适的参数σ.

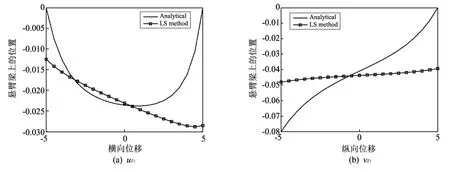
图3 边界Γ1上的有限元参考解以及最小二乘解（δ=5%） Fig.3 Analytical solution with FEM and LS solution（δ=5%）

图4 边界Γ1上的有限元参考解以及Tikhonov正则解（δ=5%） Fig.4 Analytical solution with FEM and Tikhonov regularization solution（δ=5%）

4.2 算法的有效性及稳定性验证

本小节对柯西边界上的数据施加不同水平的扰动，考察解的稳定性.假定模型的长度为L=20，对边界Γ4上的位移施加不同水平（直至10%）的随机扰动，并应用基于有限元方法广义边界控制求解.图5给出了不同扰动水平下的求解结果且整个问题域上的相对均方根误差（RSE）也在表1中给出.从图5和表1可看出，对于不同水平的随机扰动，数值方法是非常稳定的.且当扰动水平已达10%时，数值解依然很好地吻合参考解.

表1 不同扰动水平下的相对平方根误差Tab.1 The RSE against various noise levels

求解左边界上的位移是通过右边界上的柯西数据控制的，数值方法的灵敏度理论上会随着模型长度的增加而降低.接下来对算法的灵敏度进行测试.在扰动水平分别为δ=1%以及δ=5%的情况下，逐渐增加梁的长度来检验算法的灵敏度.表2给出了测试不同长度模型所对应的相对均方根误差.从表2可以看出，无论对于实验中的哪种长宽比例，广义边界控制方法都是十分有效的.正如预料，随着梁模型的增长相对误差也是逐渐加大的.但即便长宽比高达6∶1且扰动水平为5%，数值解仍然可以较好地吻合参考解.

表2 不同长宽比下的相对均方根误差 Tab.2 The RSE with different length-width ratio

图5 参考解及不同扰动水平下的数值解 Fig.5 Analytical solution and numerical solutions against different noise levels

5 结 论

本文提出了一个基于有限元方法求解柯西反问题的精确有效且稳定的数值方法.首次引入了广义边界控制的思想，将问题域未知边界上位移的求解转化成求解包含一组参数化后未知系数的线性代数方程组的直接方法.Tikhonov正则化有效地克服了随机扰动带来的不适定性.数值论证说明了基于有限元方法的广义边界控制是有效且稳定的.由于算法具有很好的鲁棒性，因此对于求解实际应用中的反问题是非常有用的.

［1］Liu G R，Han X.Computational inverse techniques in nondestructive evalution［M］.Florida：CRC Press，2003.

［2］Eldén L，Berntsson F.A stability estimate for a Cauchy problem for an elliptic partial differential equations［J］.Inverse Probl.，2005，21（5）：1643-1653.

［3］Hon Y C，Li M.A computational method for inverse free boundary determination problem［J］.Int.J.Numer.Meth.Eng.2008，73（9）：1291-1309.

［4］Hon Y C，Li M.A discrepancy principle for the source points location in using the MFS for solving BHCP［J］.Int.J.Comput.Meth.，2009，6（2）：181-197.

［5］Hon Y C，Wei T.A fundamental solution method for inverse heat conduction problem［J］.Eng.Anal.Bound.Elem.，2004，28（5）：489-495.

［6］Ling L，Takeuchi T.Boundary control for inverse Cauchy problems of the Laplace equations［J］.CMES，2008，29：45-54.

［7］Wei T，Hon Y C，Ling L.Method of fundamental solutions with regularization techniques for Cauchy problems of elliptic operators［J］.Eng.Anal.Bound.Elem.，2007，31（4）：373-385.

［8］Zhang H W，Wei T.Two iterative methods for a Cauchy problem of the elliptic equation with variable coefficients in a strip region［J］.Numer Algorithms，2014，65（4）：875-892.

［9］Schaback R.Solving the Laplace equation by meshless collocation using harmonic kernles［J］.Adv.Comput.Math.，2009，31（4）：457-470.

［10］Lawson C L，Hanson R J.Solving least squares problems［M］.Philadephia：SIAM，1995.

［11］Kalman D.Singular valuable decomposition：the SVD of a matrix［J］.The College Mathematics Journal，1996，27：2-23.

［12］Hansen P C.The L-curve and its use in the numerical treatment of inverse problems［J］.Computational Inverse Problems in Electrocardiology，2001：119-142.

［13］Hansen P C，O′Leary D P.The use of the L-curve in the regularization of discrete ill-posed problems［J］.SIAM J.Sci.Comput.，1993，14（6）：1487-1503.

［14］Hansen P C.Regularization tools：a matlab package for analysis and solution of discrete ill-posed problems［J］.Numer Algorithms，1994，6（1）：1-35.