具有反馈控制的多种群捕食-竞争系统的持久性

王丽丽，程永玲

（山西大学商务学院 理学系，山西 太原030031）

Lotka-Volterra系统在生物数学中起着重要作用.近几年，很多学者对该系统的概周期解，持久性和全局稳定性进行了广泛的研究［1-16］.在文献［1］中，Zhou Z，和Zou X研究了离散周期逻辑方程（1）的持久性和周期稳定解的存在性.

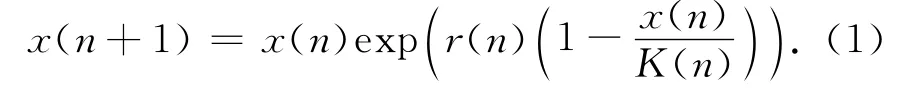
文献［2］利用泛函理论研究了具有时滞的概周期Lotka-Volterra竞争系统正概周期解的唯一性.文献［3］研究了具有时滞的多种群捕食和竞争系统的持久性.最近，具有反馈控制的Lotka-Volterra系统得到了极大关注［4-6］.文献［4］提出了具有反馈控制的单种群离散模型（2），研究了模型的持久性.

文献［5］研究了具有时滞和反馈控制的非自治单种群离散系统的持久性，在所得到的结论中，发现反馈控制对持久性是无害的.

本文考虑系统

系统（3）具有初始条件

令

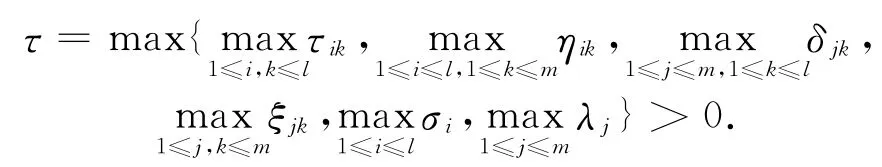
为方便，先介绍与本文相关的记号和定义.对任意的有界函数x（n），记

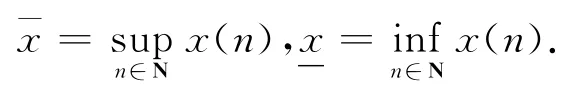
定义1 若存在正常数Mi，mi（i=1，2，3，4）使得对系统（3）的任意正解

都有

则称系统（3）是持久的.

考虑差分方程

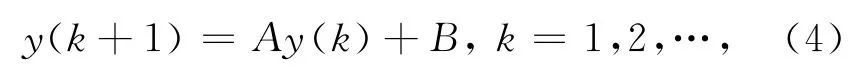
式中：A，B为正常数.

引理1［4］假定|A|＜1，且对任意的初始值y（0），存在方程（4）的唯一解y（k），表示为

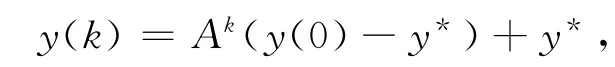
引理2［7］假定x（n）满足x（n）＞0，且当n∈［n1，∞）时，

其中，a为使得a K＞1的常数.

定理1 假定H1～H3成立，则对系统（3）的任意正解，存在正常数Mi，Pi，Wj，Qj使得

其中

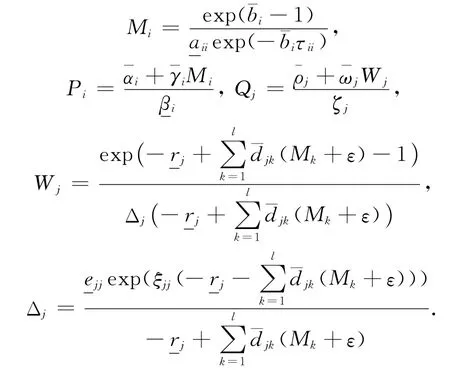
证明 根据系统（3）的第1个方程，有

进而

即

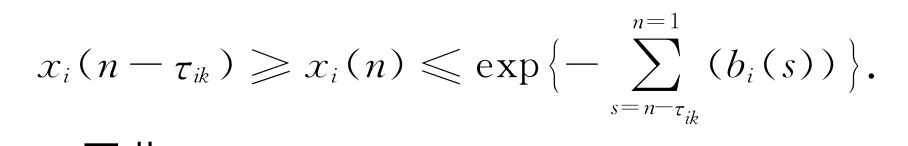
因此

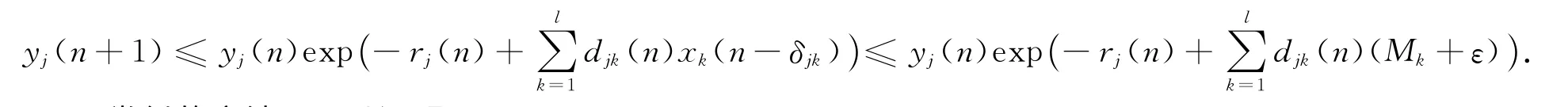
用类似的方法，可以证明

于是

由引理2，有lni→m∞yj（n）≤Wj.由系统（3）的第3个方程，有

由引理1以及差分方程比较定理，可得

定理2 假定H1～H3成立，且

则对系统（3）的任意正解，存在正常数mi，pi，wj，qj，使得

其中

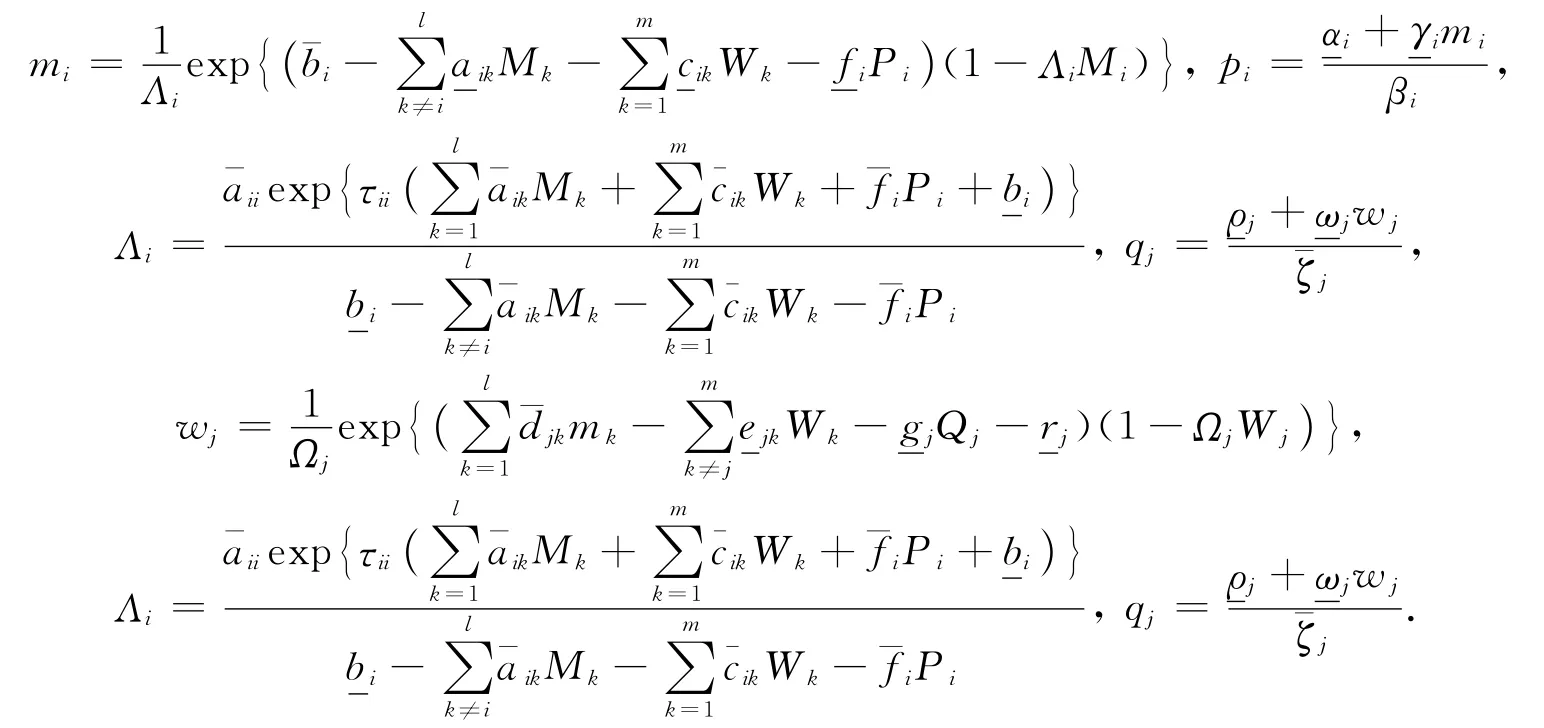
证明 由定理1，对任意的ε＞0，存在常数n1∈N，使得当n＞n1时，有

ui（n）≤Pi+ε，vj（n）≤Qj+ε，因此，对系统（3）的第1个方程，有

于是当n≥τii时，有

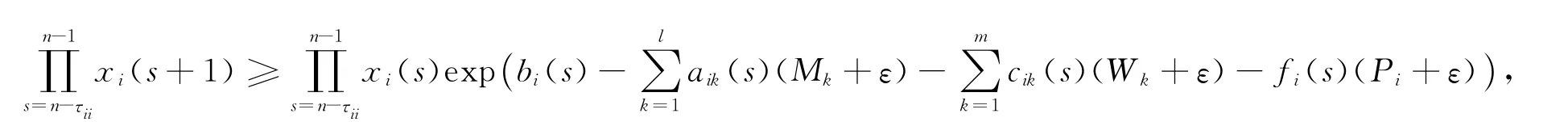
所以

进一步，可以得到

用类似的方法，可以得到

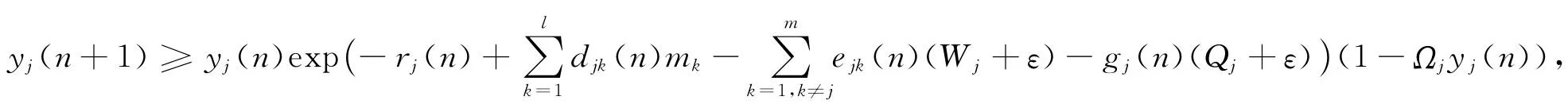
于是，由引理3，有lni→m∞inf yj（n）≥wj.

对充分小的ε＞0，由系统（3）的第3个方程，有

由引理1以及差分方程的比较原理，可得

在式（6）中令ε→0，可得

同理，对系统（3）的第4个方程，可得

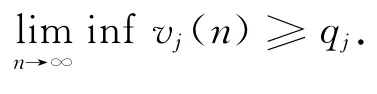
证毕.

根据定理1和定理2的结论，可知系统（3）是持久的.

［1］Zhou Z，Zou X.Stable periodic solutions in a discrete periodic logistic equation［J］.Appl.Math.Lett.，2003，16（2）：165-171.

［2］Li Z，Chen F D，He M X.Almost periodic solutions of a discrete Lotka-Volterra competi tion system with dealys［J］.Nonlinear Anal.RWA，2011，12（4）：2344-2355.

［3］Liao X Y，Zhou S F，Raffoul Y N.On the discretetime multi-species competition-preda tionsystem with several delays［J］.Appl.Math.Lett.，2008，21（1）：15-22.

［4］Chen F D.Permanence of a single discrete model with feedback control and delay［J］.Appl.Math.Lett.，2007，20（7）：729-733.

［5］Xu J B，Teng Z D.Permanence for nonautonomous discrete single-species system with delays and feedback control［J］.Appl.Math.Lett.，2010，23（9）：949-954.

［6］Chen F D.Permanence in nonautonomous multi-species predator-prey system with feed back controls［J］.Appl.Math.Comput.，2006，173（2）：694-709.

［7］Yang X.Uniform persistence and periodic solutions for a discrete predator-prey system with dealys［J］.J.Math.Anal.Appl.，2006，316（1）：161-177.

［8］Chen F D.Permanence and global attractivity of a discrete multispecies Lotka-Volterra competition predator-prey systems［J］.Appl.Math.Comput.，2006，182（1）：3-12.

［9］Liao X Y，Zhou S F，Chen Y M.Permanence for a discrete time Lotka-Volterra type food-chain model with delays［J］.Appl.Math.Comput.，2007，186（1）：279-285.

［10］Chen L S，Lu Z，Wang W D.The effect of delays on the permanence for Lotka-Volterra systems［J］.Appl.Math.Lett.，1995，8（4）：71-73.

［11］Muroya Y.Persistence and global stability for discrete models of nonautonomous Lotka-Volterra type［J］.J.Math.Anal.Appl.，2002，273（2）：492-511.

［12］Muroya Y.Persistence and global stability in discrete models of pure-delay nonautonomous Lotka-Volterra type［J］.J.Math.Anal.Appl.，2004，293（2）：446-461.

［13］Li Y K.Positive periodic solutions of discrete Lotka-Volterra competition systems with state dependent and distributed delays［J］.Appl.Math.Comput.，2007，190（1）：526-531.

［14］Zeng X Y，Shi B，Gai M J.A discrete periodic Lotka-Volterra system with delays［J］.Comput.Math.Appl.，2004，47（4）：491-500.

［15］Fang N，Chen X X.Permanence of a discrete multispecies Lotka-Volterra competition predator-prey system with delays［J］.Nonlinear Anal.RWA，2008，9（5）：2185-2195.

［16］Muroya Y.Persistence and global stability in discrete models of Lotka-Volterra type［J］.J.Math.Anal.Appl.，2007，330（1）：24-33.