分数阶Timoshenko梁格点系统解的存在唯一性

王 静，魏毅强

（太原理工大学 数学学院，山西 太原030024）

格点系统［1］是一类很重要的无穷维动力系统，是含有离散变量的时空系统，也是由无穷多个常微分方程或差分方程构成的系统.格点系统在许多领域中都有广泛应用，例如生物学［2］、电子工程［3］、激光系统［4］、材料科学［5］、化学反应理论［6］、图像处理和模式识别等［7-8］.近些年来，许多人对格点动力系统的非线性项做了不同假设，主要是为了研究格点动力系统的解的性质，如行波解方面的研究，格点系统的解的混沌性质研究等.最近，一些研究者开始密切关注格点动力系统的解的渐近行为，如上半连续性，吸引子的存在性，分形维数等，且已经有很多关于格点动力系统的全局吸引子、一致吸引子、拉回吸引子的研究.但这些吸引子在吸引轨道的速度上有时很慢.而指数吸引子是包含全局吸引子且具有有限维数、指数吸引所有有界集的正不变集，是研究动力系统渐近行为的有效工具.有关格点动力系统的指数吸引子的研究，A.Y.Abdallah、范小明、赵才地等得到一些重要结果，可参看文献［9-11］.可见，研究格点动力系统具有重要的理论和实际指导意义.

众所周知，梁是大型空间结构中的基本组件之一，所以梁的振动问题一直是科学关注的热点.Timoshenko梁是目前较为流行的柔型结构梁模型之一.Timoshenko梁理论是由Timoshenko在1921～1922年提出的，这个理论同时考虑了梁的剪切变形和梁的弯曲变形引起的转动惯量，并被广泛地运用到很多实际工程上.到目前为止，已有许多学者对Timoshenko梁做了一定的研究.如李根国、朱正佑等分析了非线性粘弹性Timoshenko梁动力学行为［12］和具有分数导数本构关系的粘弹性Timoshenko梁静动力学行为［13］；裴君莹等研究了两端固定的Timoshenko梁［14］；刘维宁等研究了移动荷载作用下周期支承的Timoshenko梁动力响应［15］；翁雪涛等研究了弹性支持的无限Timoshenko梁对移动振动质量的响应［16］.但目前还没有关于Timoshenko梁格点系统的研究，鉴于Timoshenko梁应用的广泛性和格点系统的理论及实际指导意义.本文研究了分数阶Timoshenko梁格点系统解的存在唯一性.

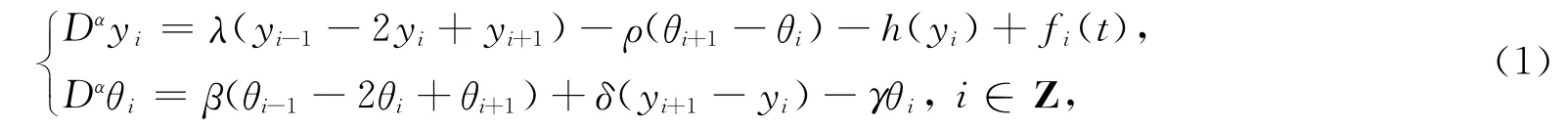
1 预备知识

定义1［17］函数x的α阶积分定义为

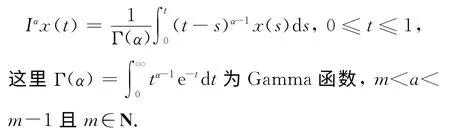
定义2［17］函数x的α阶Caputo型导数定义为

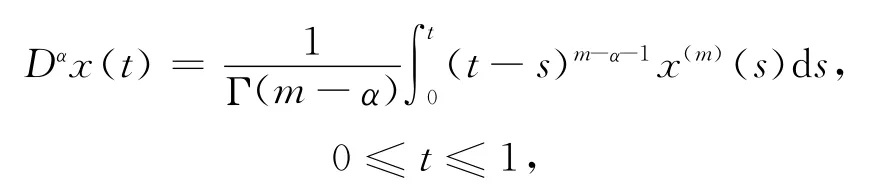
这里m＜a＜m-1且m∈N.

定理1［18］（Banach压缩映射原理）设X是完备的度量空间，T是X上的压缩映射，那么T有且只有一个不动点（即方程Tx=x有且只有一个解）.

定理2［19］（Arzela-Ascoli定理）设G是带有切比雪夫范数的C［a，b］上的一个子集，那么G在C［a，b］上相对紧当且仅当G等度连续且一致有界.

注1 如果对任意的ε＞0，存在某δ＞0，使得对所有的g∈G和所有的x1，x2∈［a，b］，当|x1-x2|＜δ时，有|g（x1）-g（x2）|＜ε，那么集合G等度连续.

注2 如果存在一个常数M＞0，使得对所有的g∈G都有‖g‖∞≤M，那么集合G一致有界.

定理3［20］（Schauder's不动点定理）设（E，d）是一个完备度量空间，U是E上的闭凸集，A∶U→U，若｛Au∶u∈U｝是E上的相对紧集.那么A至少有一个不动点.

下面主要考虑系统（1），当1＜a＜2时，在初值条件

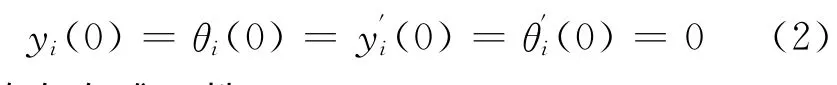
下解的存在唯一性.

系统（1）可以看成系统（3）对空间的离散化模型

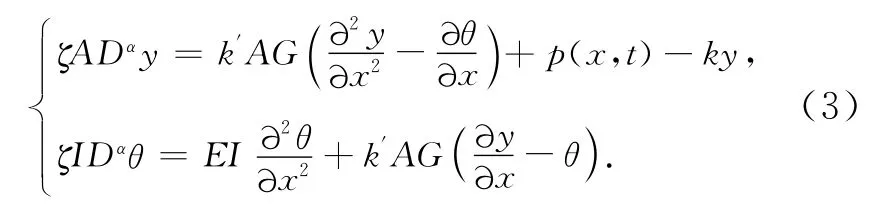
系统（3）是在考虑梁的剪切变形和转动惯量情况下，弹性基础上的无限Timoshenko梁的弯曲振动方程，初始条件为静止在平衡位置.式中：y为梁的横向位移；p为作用于单位长度梁上的力，与时间和位置有关；E为梁的杨氏模量；I为横截面的惯性矩；ζ为梁的密度；k′为剪切系数；A为横截面积；G为梁的剪切模量；k为地基的刚度；作用力p（x，t）包括振动质量原有的激励力和质量随梁一起振动所产生的惯性力.

系统（1）～（2）中，Dα为Caputo分数阶导数，且1＜α＜2，Z是整数集，λ，ρ，β，δ，γ是正常数，f（t）=（fi（t））i∈Z∈l2是满足某些条件的非线性函数，h是一个光滑函数，对所有的s∈R及正常数C满足

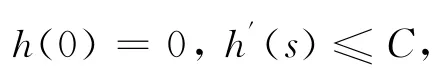
y=（yi）i∈Z∈l2和θ=（θi）i∈Z∈l2是两个序列，l2

表示通常的实序列空间.其定义如下l2上的内积和范数定义如下

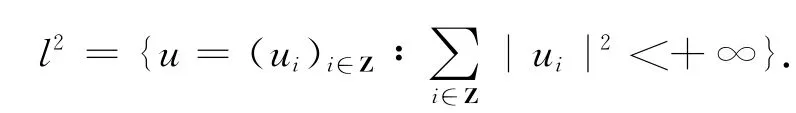
本文在H=l2×l2空间上讨论分数阶系统（1）～（2），令Φ=（y，θ）T∈l2×l2，定义l2×l2中的内积和范数如下

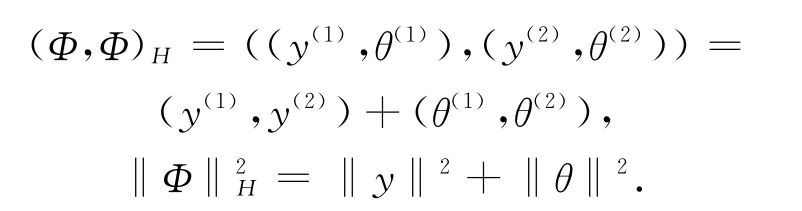
对于任给y=（yi）i∈Z∈l2和θ=（θi）i∈Z∈l2，定义l2上的线性算子

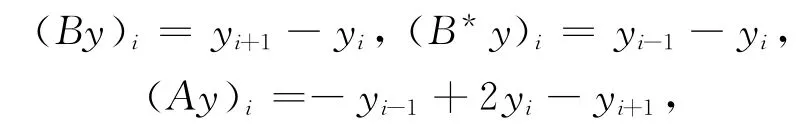
则可推出

及

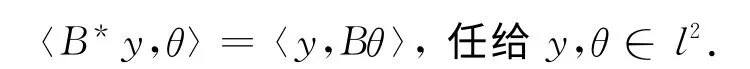
令y=（yi）i∈Z∈l2，θ=（θi）i∈Z∈l2，系统（1）～（2）就与下面形式的方程等价

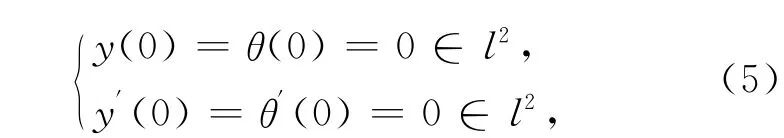
初值条件为令Φ=（y，θ）T，G（t，Φ）=（-h（y）+f（t），0）T，Φ（0）=Φ′（0）=（0，0）T，则系统（4）～（5）转化成空间H中的抽象常微分方程

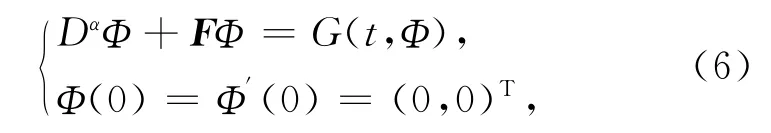
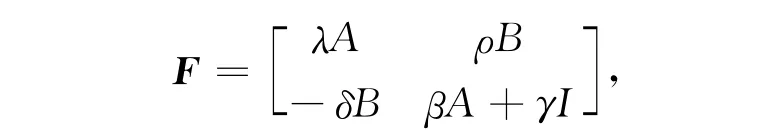
其中则系统（1）～（2）的解的存在唯一性问题的证明转化为证明系统（6）的解的存在唯一性问题.

2 主要结论

对任意的a＞0，令

并记

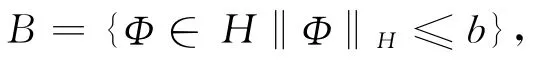
其中，a，b均为常数，‖Φ‖2H=‖y‖2+‖θ‖2，任给Φ=（y，θ）T∈H，而y，θ∈l2.现定义

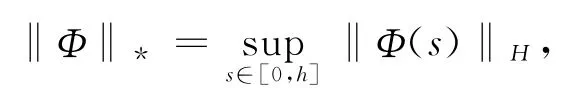
其中，h是给定的满足一定条件的正常数.

引理1 对于Φ∈B及t∈J成立

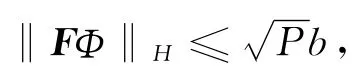
其中

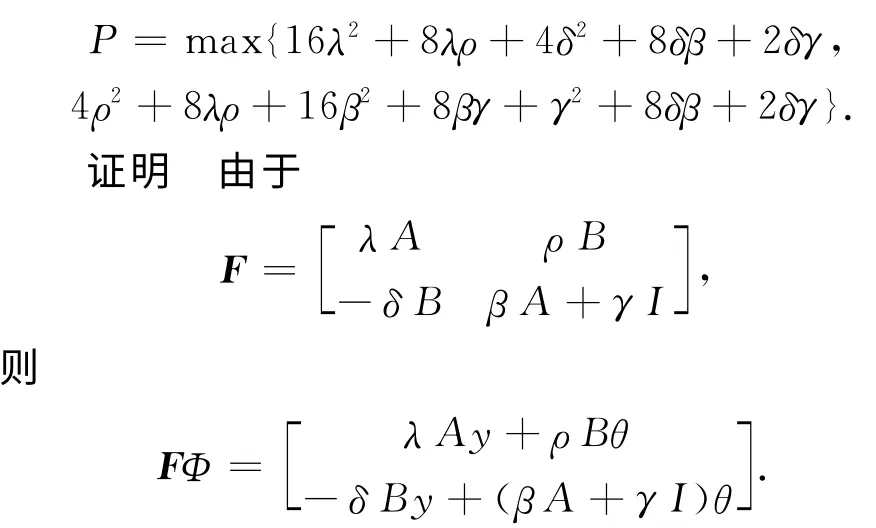
由此可知

取

则

又由于Φ∈B，及t∈J，故可得

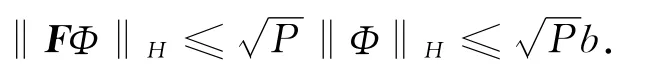
证毕.

引理2 对于Φ∈B及t∈J，有

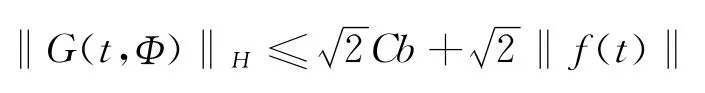
成立.

证明 由于G（t，Φ）=（-h（y）+f（t），0）T，则有

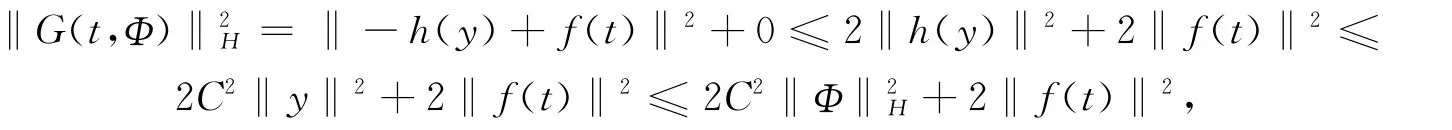
那么

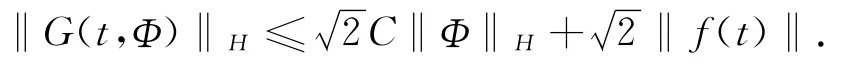
又由于Φ∈B及t∈J，故可得

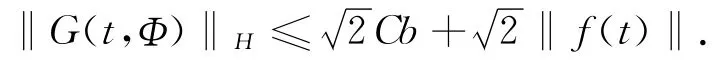
证毕.

引理3 对于0＜σ≤1及0＜c≤d，有

成立.

（H）假设存在某正常数β∈（0，α），使得实值函数

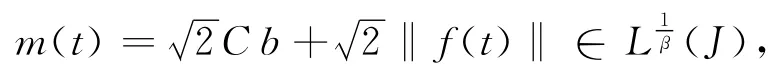
满足如下条件

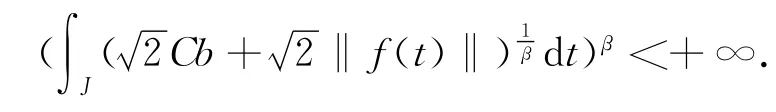
进一步，假设下面的三个条件也成立：

（H 1）G（t，Φ）-FΦ在J上关于t是勒贝格可测的；

（H 2）G（t，Φ），FΦ分别在B上关于Φ是连续的；

注 条件（H 1），（H 2）显然成立，由引理1，引理2及（H）可知条件（H 3）也成立.

定理4 假设条件（H 1），（H 2），（H 3）均成立，那么对α∈（1，2），初值问题（6）在区间［0，h］上至少存在一个解，其中

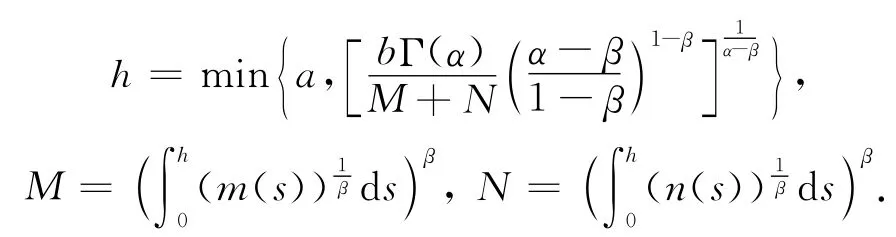
证明 由Caputo算子的定义及性质可知，系统（6）的解的存在唯一性问题等价于下面积分方程的解的存在唯一性问题

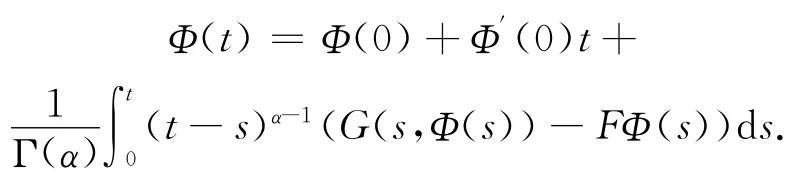
由Φ（0）=Φ′（0）=（0，0）T即得

记

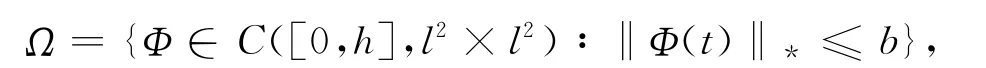
在Ω上定义算子T如下

其中，Φ∈Ω，t∈［0，h］.

首先证明T是自映射的，即对任给Φ∈Ω，有TΦ∈Ω.

而

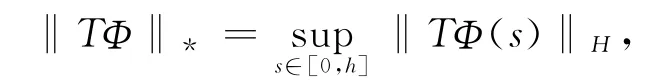
故

即T是自映射的.

其次证明算子T是全连续的（此部分分两步给出证明）.

（i）证明算子T是连续的.

对任给Φm，Φ∈Ω，m=1，2，…，当m→∞时，

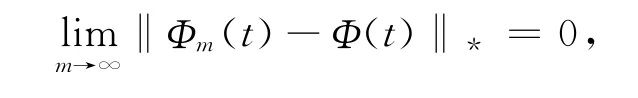
可得

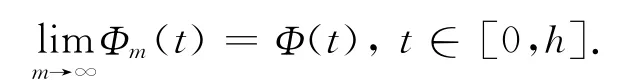
因此，由条件（H 2）得

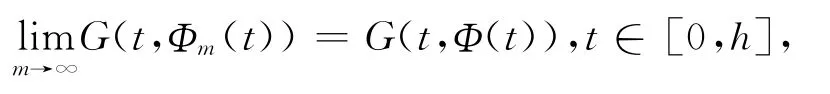
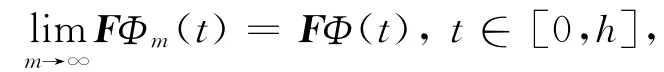
于是可知

及

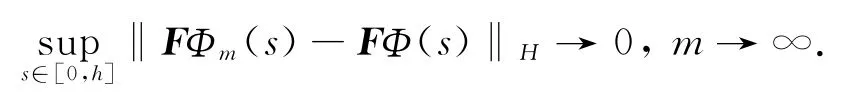
另一方面，

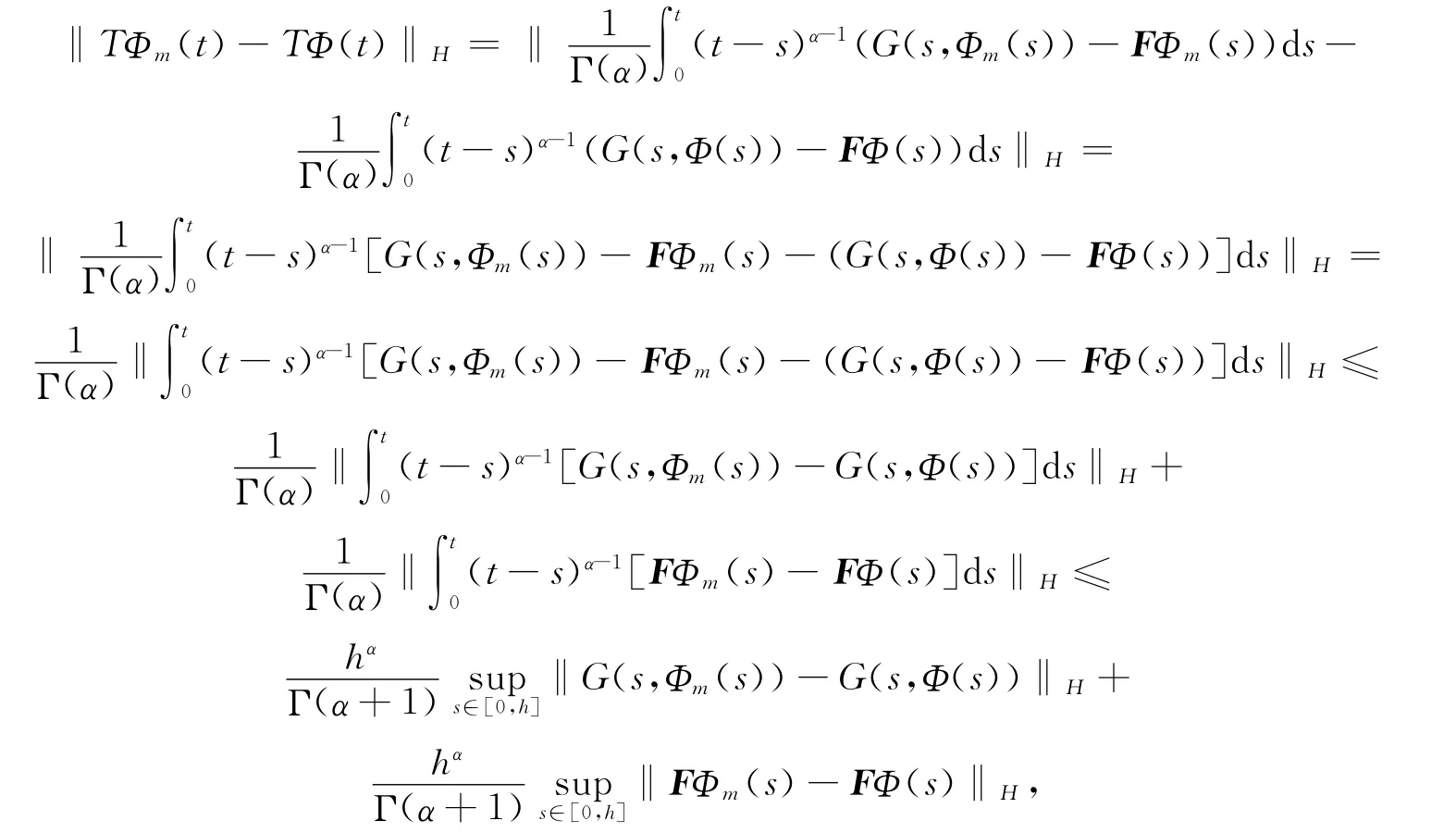
因此

故T是连续的.

（ii）证明TΩ是相对紧的.

（a）对任给Φ∈Ω，

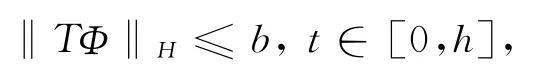
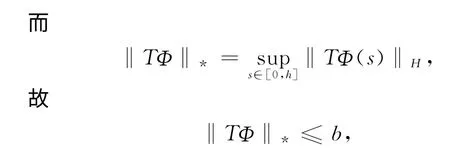
因此可

（b）对任给t1，t2∈［0，h］，t1≤t2，有

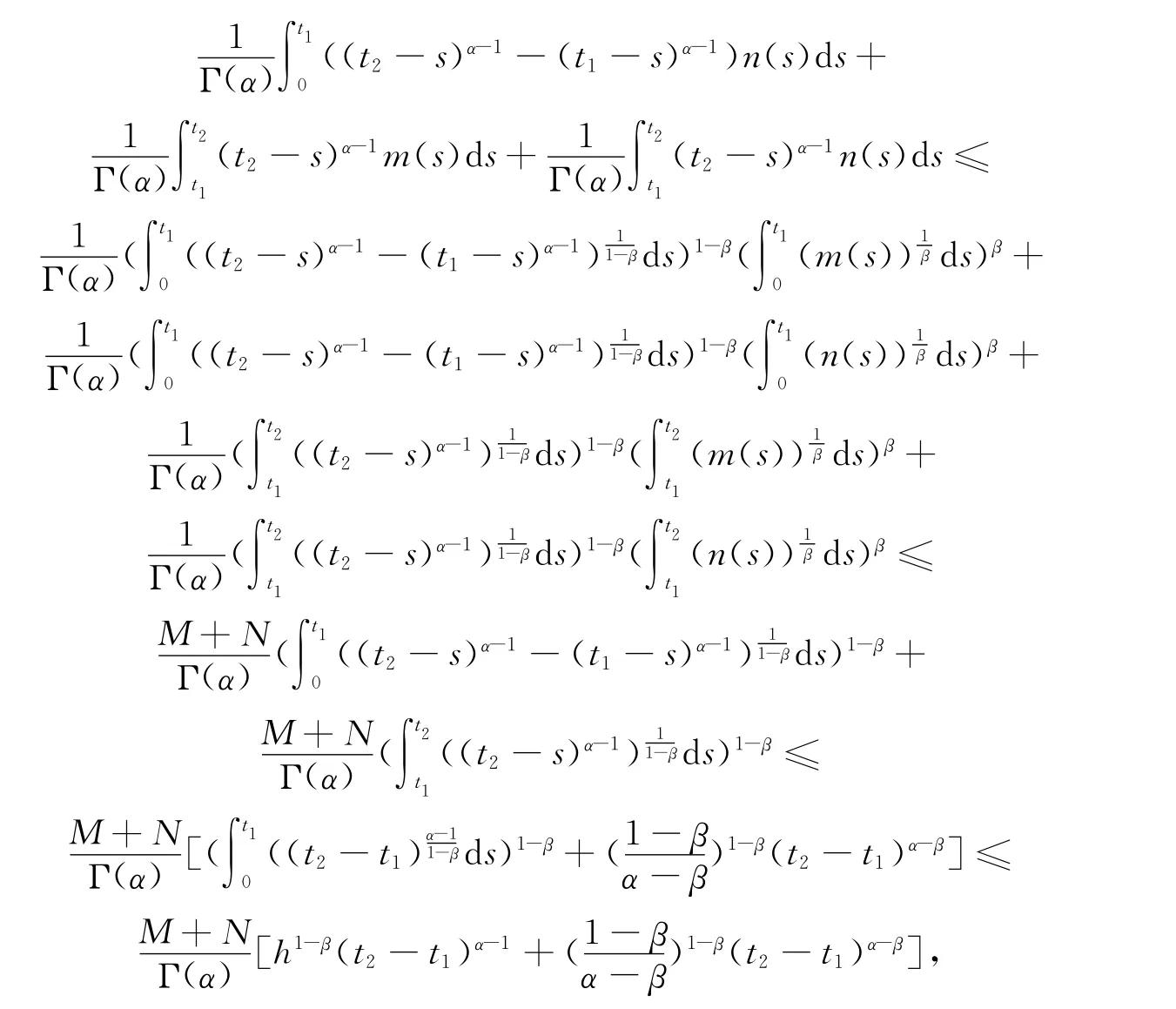
故

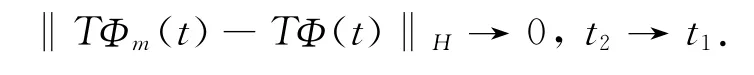
因此即得｛TΦ∶Φ∈Ω｝是等度连续的.于是由Ascoli-Arzela即可知TΦ是相对紧的.再由Schauder不动点定理可知存在Φ＊∈Ω，使得

即

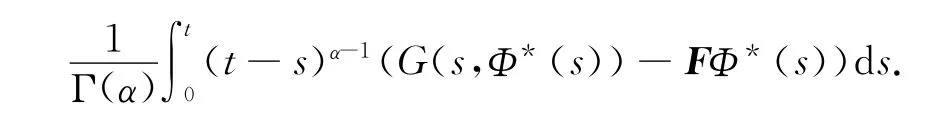
故初值问题（6）在区间［0，h］上至少存在一个解.

证毕.

推论1 令（G（t，Φ）-FΦ）∈C（J×B，H），对任给α∈（1，2），初值问题（6）在区间［0，h′］上至少存在一个解.其中

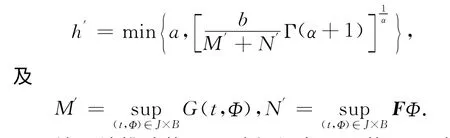
注 该推论的证明过程与定理4的证明过程类似，在此省略.

定理5 假设（H1），（H2）成立，并假设

及

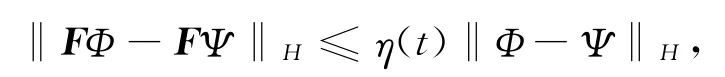
其中Φ，Ψ∈B，t∈J.则原初值问题在区间［0，h1］上存在唯一解.其中

证明 记

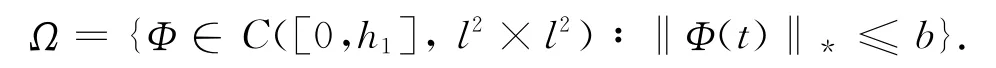
对于给定的Φ∈Ω，类似地在Ω上定义算子T如下

其中，t∈［0，h1］.类似地可以证明在［0，h1］上，T是自映射的.

接下来证明T是压缩的.

事实上，对任给Φ，Ψ∈Ω，有

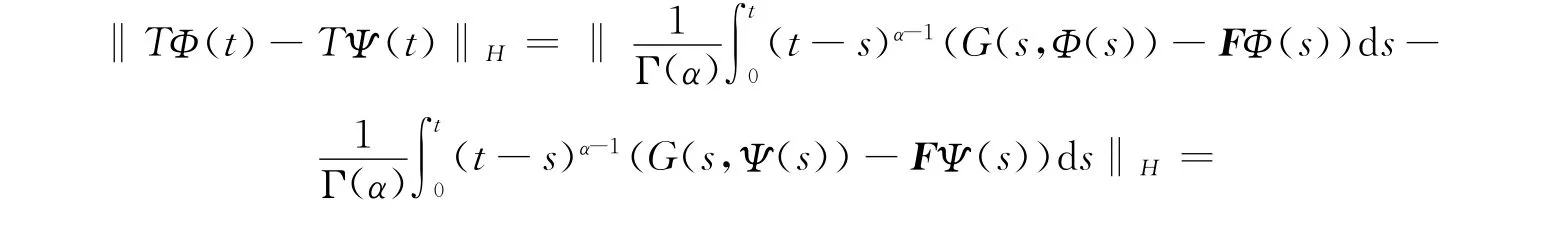
于是可知

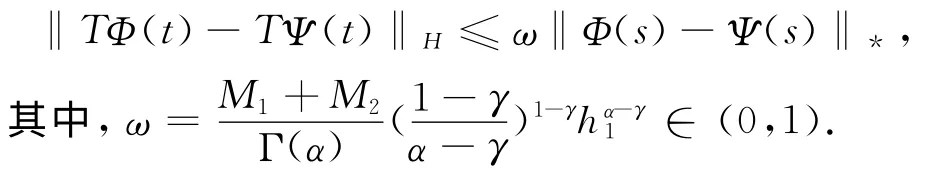
故由Banach压缩映射原理可知，T在［0，h1］上有唯一不动点，即原初值问题在区间［0，h1］上存在唯一解.

证毕.

推论2 令（G（t，Φ）-FΦ）∈C（J×B，H），对任给t∈J及Φ，Ψ∈B，α∈（1，2），假设存在常数L1，L2＞0，使得

那么初值问题（6）在区间［0，h1′］上存在唯一解，其中

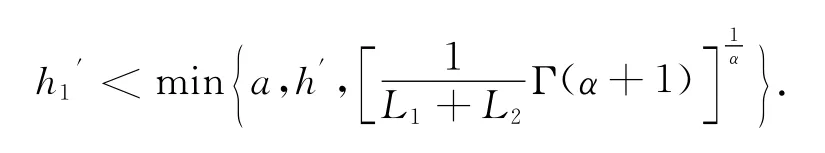
注 该推论的证明过程与定理5的证明过程类似，在此省略.

定理6 假设（H 4）成立，如果Φ（t）是原初值问题在区间［0，h］上的解，那么Φ（t）是唯一的.其中

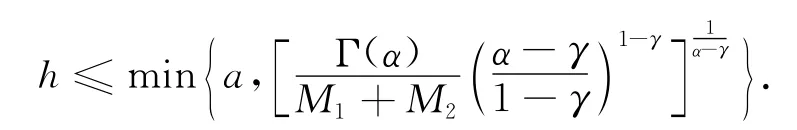
证明 假设Φ（t）和Ψ（t）均是初值问题（6）在区间［0，h］上的解，则对任给t∈［0，h］有

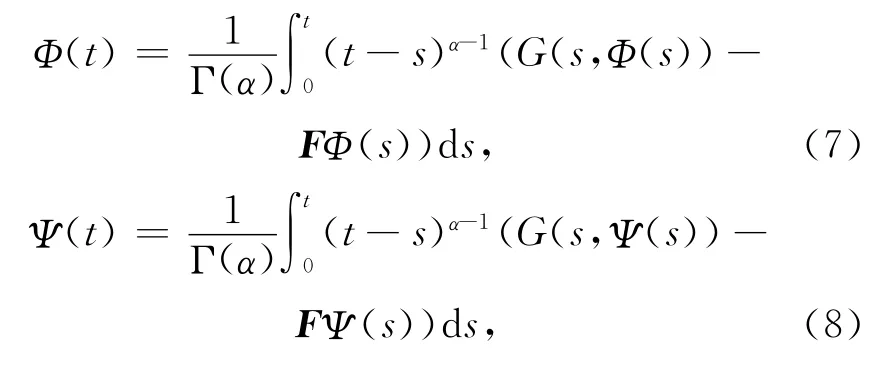
将式（7）和式（8）相减可得

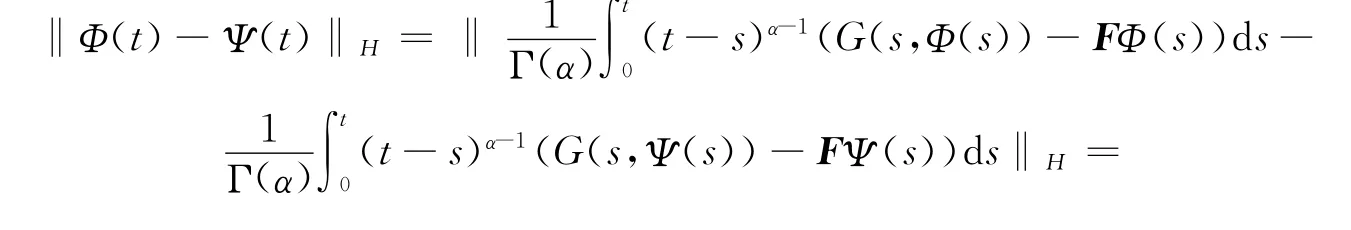
又由条件（H 4）可得

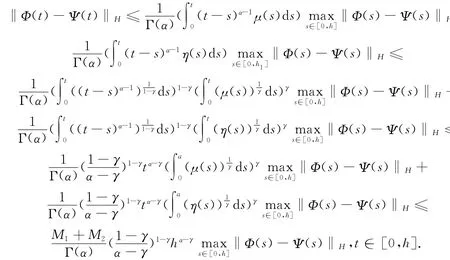
因此

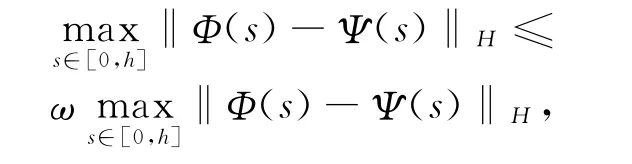
其中

故可知

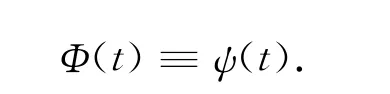
证毕.

［1］周小鹏.三类非自治无穷格点系统的一致指数吸引子［D］.湘潭：湘潭大学，2013.

［2］Keener J P.Propagation and its failure in coupled systems of discrete excitable cells［J］.SIAM Journal on Applied Mathematics，1987，47（3）：556-572.

［3］Chow S N，Paret J M.Pattern formation and spatial chaos in lattice dynamical systems-Part I［J］.IEEE Transactions on Circuits and Systems I：Fundamental Theory and Applications，1995，42（10）：746-751.

［4］Fabiny L，Colet P，Roy R.Coherence and phase dynamics of spatially coupled solidstate lasers［J］.Physical Review A，1993，47（5）：4287-4296.

［5］Cahn J W.Theory of crystal growth and interface motion in crystalline materials［J］.Acta Metallurgica，1960，8（8）：554-562.

［6］Erneux T，Nicolis G.Propagating waves in discrete bistable reaction-diffusion systems［J］.Physica，1993，67（1-3）：237-244.

［7］Chow S N，Mallet-Paret J，Van Vleck E S.Pattern formation and spatial chaos in spatially discrete evolution equations［J］.Random and Computational Dynamics，1996，4（2-3）：109-178.

［8］Chua L O，Yang L.Cellular neural networks：theory［J］.IEEE transactions on circuits and systems，1988，35（10）：1257-1272.

［9］Abdallah A Y.Asymptotic behavior of the Klein-Gordon-Schrodinger lattice dynamical systems［J］.Communications on Pure and Applied Analysis，2006，5（1）：55-69.

［10］Fan Xiaoming.Exponential attractors for lattice dynamical systems in weighted spaces［J］.Discrete and Continuous Dynamical Systems，2011，31（2）：445-467.

［11］赵才地，周盛凡.格点系统存在指数吸引子的充分条件及应用［J］.数学学报中文版，2010，53（2）：233-242.Zhao Caidi，Zhou Shengfan.Sufficient conditions for the existence of exponential attractors for lattice systems and applications［J］.Acta Mathematic Sinica，Chinese Series，2010，53（2）：233-242.（in Chinese）

［12］李根国，朱正佑，程昌钧.非线性粘弹性Timoshenko梁动力学行为的分析［J］.力学季刊，2001，22（3）：346-351.Li Genguo，Zhu Zhengyou，Cheng Changjun.Analysis of dynamical behavior of nonlinear viscoelastic Timoshenko beam［J］.Chinese Quarterly of Mechanics，2001，22（3）：346-351.（in Chinese）

［13］朱正佑，李根国，程昌钧.具有分数导数本构关系的粘弹性Timoshenko梁静动力学行为分析［J］.应用数学和力学，2002，23（1）：1-10.Zhu Zhengyou，Li Genguo，Cheng Changjun.Quasi-Static and dynamical analysis for viscoelastic Timoshenko beam with fractional derivative constitutive relation［J］.Applied Mathematics and Mechanics，2002，23（1）：1-10.（in Chinese）

［14］裴君莹，刘三阳.两端固定的Timoshenko梁［J］.西安电子科技大学学报（自然科学版），2002，29（6）：822-826.Pei Junying，Liu Sanyang.The solution of the Timoshenko beam with two fixed ends［J］.Journal of Xidian University，2002，29（6）：822-826.（in Chinese）

［15］刘维宁，张昀青，孙晓静.移动荷载作用下周期支承的Timoshenko梁动力响应［J］.中国铁道科学，2006，27（1）：38-42.Liu Weining，Zhang Yunqing，Sun Xiaojing.Dynamic response of periodic supported Timoshenko beam under moving load［J］.China Rail Way Science，2006，27（1）：38-42.（in Chinese）

［16］翁雪涛，胡安.弹性支持的无限铁木辛柯梁对移动振动质量的响应［J］.海军工程大学学报，2008，20（1）：65-69.Weng Xuetao，Hu An.Response of an elastically supported infinite Timoshenko beam to moving vibrating mass［J］.Journal of Naval University of Engineering，2008，20（1）：65-69.（in Chinese）

［17］Deng Jiqin，Ma Lifeng.Existence and uniqueness of solutions of initial value problems for nonlinear fractional differential equations［J］.Applied Mathematics Letters，2010，23（6）：676-680.

［18］程其襄，张奠宙，魏国强，等.实变函数与泛函分析基础［M］.北京：高等教育出版社，2010.

［19］Kilbas A A，Srivastava H M，Trujillo J J.Theory and applications of fractional differential equations［M］.Netherlands：Library of Congress Cataloging，2006.

［20］Morel J M，Takens F，Teissier B.The analysis of fractional differential equations［M］.Germany：Springer-Verlag，2010.