各向异性油藏水平井多角度人工裂缝线性单元计算方法

方思冬，程林松，辛一男，何聪鸽

（1.中国石油大学（北京）石油工程学院，北京 102249；2.中国石油勘探开发研究院，北京 100083）

文章编号：1001⁃246X（2015）05⁃0595⁃08

各向异性油藏水平井多角度人工裂缝线性单元计算方法

方思冬1，程林松1，辛一男1，何聪鸽2

（1.中国石油大学（北京）石油工程学院，北京 102249；2.中国石油勘探开发研究院，北京 100083）

考虑各向异性油藏渗透率张量的表征，利用Green函数和拉普拉斯变换建立裂缝流动的一维单元，裂缝的流量分布采用节点线性插值，裂缝内的流动处理为线性积分，耦合地层与人工裂缝的流动，建立有限导流裂缝井底压力的求解方法.结果表明：多裂缝压裂水平井存在压裂裂缝线性流、地层线性流、系统径向流3种流动形态，压裂裂缝条数越多，相同的生产时间，无因次井底压降越小；裂缝条数对流动影响明显.随着裂缝条数的增加，压降变化减小；裂缝长度和导流能力有相似的变化.人工裂缝与井筒角度越大，产能越大，当裂缝垂直于井筒时，产量最大；地层最大渗透率方向垂直于人工裂缝时产量最大，平行裂缝时产量最小.当人工裂缝垂直于井筒，并同时垂直于地层最大渗透率方向时，达到最大产量值.

各向异性油藏；压裂水平井；试井；点源函数；多角度裂缝

0 引言

目前，非常规油气藏，如致密油气藏以及页岩气藏，普遍采用压裂水平井进行开发［1－2］.国外一部分学者主要利用Gringarten［3－4］提出的源函数方法求解压力动态，如Evans和Guo［5］利用实空间的点源函数和Newman乘积原理得到了有多条裂缝的水平井压力动态.Rbeawi［6］利用Green函数求解均质油藏中具有多条倾斜裂缝压裂水平井的压力分布.Valko［7－8］和Zhu［9］建立了体积源函数，并通过该方法得到了多条裂缝压裂水平井的半解析解.其他一些学者主要采用拉普拉斯变换和数值反演求解不同情况下的压力动态，如Ozkan［10－12］建立了拉氏空间内考虑不同的井型、边界类型以及不同油藏类型的试井模型，Raghavan［13－14］利用盒状地层拉氏空间点源解，采用叠加原理得到了多条裂缝压裂水平井拉氏空间解.Brown［15］提出利用三线性流模型研究非常规油气藏的压裂水平井动态，该模型计算简便，物理过程清晰，但无法准确表征压裂水平井各个流动阶段.而对于各向异性油藏的研究，刘月田［16］利用坐标变换，将各向异性油藏转化为各向同性油藏进行求解.何应付［17］将各向异性坐标变换应用到边界元方法中求解封闭地层各向异性油藏压力动态.姚军［18］基于渗透率张量理论与有限元和有限差分方法进行了各向异性油藏的数值模拟研究.廉培庆［19］利用半解析解求取各向异性油藏压裂水平井产能.以前研究多裂缝压裂水平井主要是研究与井筒正交裂缝的情况，而与井筒存在不同角度的裂缝研究很少，各向异性油藏的研究主要简化成最大和最小渗透率两个方向，而缺乏对实际油藏各向异性情况的准确描述.本文吸收有限元线性单元的思想，结合源函数方法和渗透率张量对各向异性的表征，建立各向异性油藏压裂水平井压力动态的求解方法，划分流动阶段，分析各向异性和人工裂缝参数对压力动态的影响.

1 裂缝流动模型的建立和求解

1.1 物理模型

水平井穿过多条与水平井筒存在一定夹角的裂缝.整个油藏为水平等厚、均质、各向异性油藏，且最大渗透率方向与笛卡尔坐标轴方向存在一定夹角；油藏顶底封闭，只考虑无限大外边界；水平井仅在裂缝处射孔生产；水平井定产生产，不考虑井筒摩阻引起的附加压力降，各条裂缝在井筒处压力相等；水平井井筒考虑为无限导流而人工裂缝为有限导流；地层和流体微可压缩，流体为单相，且地层中流动符合达西定理；不考虑重力对流动的影响.

建立平面二维渗流的各向异性油藏渗透率张量模型，坐标轴1，2为渗透率张量的主轴，且轴1为最大渗透率方向，轴2为最小渗透率方向，并假定所取的坐标系（x，y）与（1，2）存在θ角度［20］：

式中，K1为最大渗透率，μm2；K2为最小渗透率，μm2；θ为坐标系与渗透率最大值夹角，rad；Kxy为二阶渗透率张量，μm2.

在平面渗透率张量的基础上，建立考虑渗透率张量的不稳定流渗流模型

式中，kxx，kyx，kyy为渗透率张量的分量，μm2；ϕ为孔隙度；Ct为压缩系数，1·atm－1；μ为粘度，mPa·s.引入特征变换将（2）式化简为

式中，η1＝（kyy－/kxx）/（ϕμCt）．

1.2 压裂水平井压力动态求解模型

1）油藏向人工裂缝流动模型

Gringaden［2］给出了实空间下压裂直井的线源

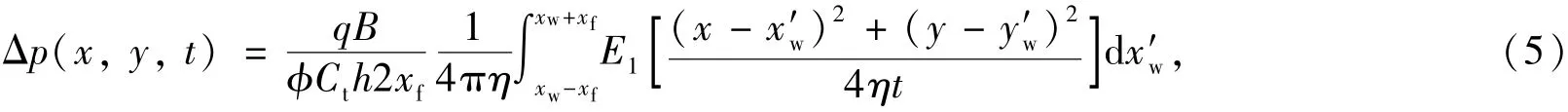
式中，q为压裂直井产量（恒定），cm3·s－1；B为体积系数，xw为井半径，cm；xf为裂缝半长，cm；h为油藏厚度，cm.

根据已有压裂直井裂缝上流量分布规律［4］，将裂缝划分成若干单元如图1所示，每个单元内流量分布根据单元两个端点线性插值构成如图2所示，基于式（5）得出油藏向裂缝单元流动压降：

图1 多级压裂人工裂缝模型Fig.1 Fractured horizontal wellmodel

图2 裂缝单元模型Fig.2 Fracture elementmodel

式中，ε＝l/lf；qe1，qe2为端点处流量强度，cm3·（s·cm－1）－1；lf为单元体长度，cm.α为裂缝与x轴夹角，rad；Δp（x，y，t）为油藏中任意一点压降，atm.将式（6）无因次化为

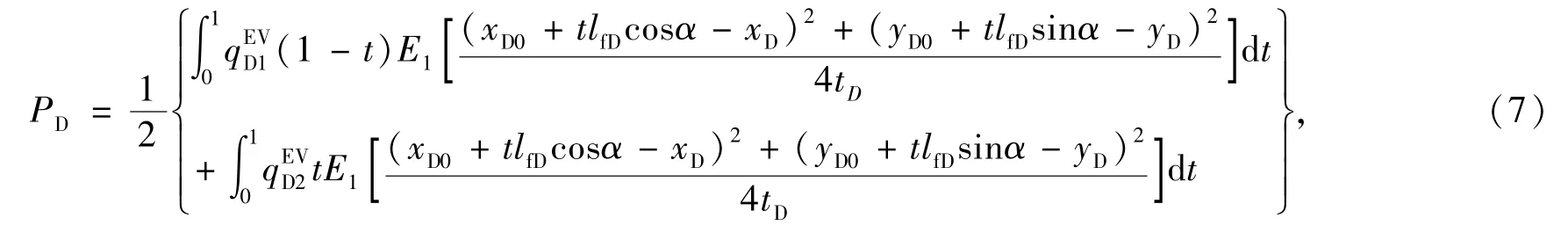
2）裂缝内流动模型

目前有限导流裂缝内流动简化为稳定线性流动［8－9，19］，根据达西定理由裂缝远端向射孔点积分，本文采用流量积分法，但流量在每个单元内由端点线性插值得到，即裂缝中任意的压力表示为

将式（10）无因次化并转换到拉普拉斯空间下

式中，CfD＝2πkxf/（kfwf）；lfD＝lf/xf．

以单条裂缝划分为4个单元为例，根据裂缝网格的对称性，建立裂缝流动附加矩阵

3）油藏渗流与裂缝内流动的耦合

数学模型中，假设压裂的裂缝条数为n，每条裂缝离散单元个数为m（i），i＝1∶n，每一条压裂裂缝都假定拥有不同的特性，并且可以在井筒的任意位置.认为压裂裂缝都在相同的井筒压力下生产，即为水平井无限导流能力模型.水平井总的流量是每一条压裂裂缝中流出流量的总和.

拉普拉斯空间下，流量和压力满足以下表达式

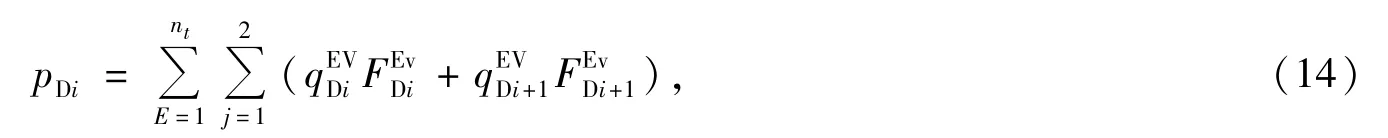
式中，nt为压裂水平井全部一维单元数.在无限导流能力的假设条件下，水平井井筒中各处保持相等的压力，

将每个单元对应式（13），（14），（15）相应的公式形式写成如下矩阵方程

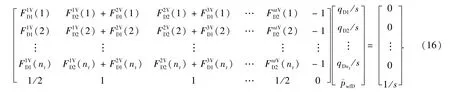
裂缝流动矩阵（12）和油藏流动矩阵（16）耦合求解，将（16）矩阵中压力部分系数矩阵表示为：AqD＝pD；式（12）裂缝的流动表示为pwfD－pD＝CqD；以上两式可以合并为（A＋C）qD＝PwfD.通过求解耦合矩阵方程组，在Laplace空间计算得到水平井井底压力之后，再利用Stehfest数值反演方法［20］可以求得实空间下压裂水平井有限导流裂缝井底压力解及每条裂缝的产量.

2 模型对比及压力动态分析

2.1 模型对比

将计算结果与经典有限导流裂缝［21］的计算结果进行对比如图3所示.选取低无因次导流能力（无因次导流系数为20）有限导流裂缝为例，该条件下裂缝内流动阻力大，流动形态复杂，与以往计算结果对比更有意义，对比不同离散网格数目下计算结果发现需要一定数量的网格才能满足求解精度，当划分线性单元数为14时，计算结果与Blasingame有限导流压力和压力导数曲线几乎重合.该模型优点在于计算精度是可控的，受网格数影响.

2.2 压力动态分析

图3 有限导流裂缝压力对比Fig.3 Finite fracture flow validation

计算前提：地层参数无因次条件，油藏为各向异性，水平渗透率为垂直渗透率2倍，水平井存在3条与井筒呈不同角度的压裂裂缝，裂缝两翼不等长.无因次参考长度选取最长裂缝半长，按照式（7）无因次化，各参数取值依次为：裂缝1半长100m；夹角60°；裂缝2半长120m；夹角90°；裂缝1半长80 m；夹角70°.分别考虑无限导流裂缝、有限导流裂缝（导流能力较大）、有限导流裂缝（导流能力较小）如图4、图5所示.

无限导流和高导流能力裂缝，流动形态分为3种：①地层线性流动阶段，是指在流动初期地层中流体线性的流向各条压裂裂缝.在双对数图上表现为无因次压力导数曲线为1/2斜率的直线段.②过渡流阶段，该阶段没有明显特征.③拟径向流动阶段，是指对于整个油藏，如果生产时间很长，且压力波未传播到边界，则流体以拟径向流的形式向水平井及压裂裂缝区域流动.该流动段在双对数诊断图上表现为无因次压力导数曲线为0.5值水平直线段.对于低导流能力裂缝，流动形态分为5种：①地层裂缝双线性流动阶段，是指在流动初期地层中流体线性的流向各条压裂裂缝，压裂裂缝内部同时存在线性流动，在双对数图上表现为无因次压力导数曲线为1/4斜率的直线段.②和④为过渡流阶段，而③为地层线性流动阶段，⑤是拟径向流动阶段.

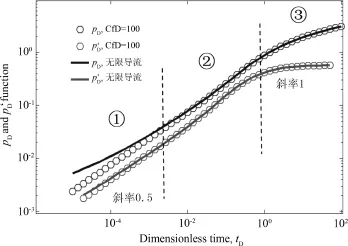
图4 无限导流与高导流裂缝压力Fig.4 Pressure of infinite and high conductive fracture

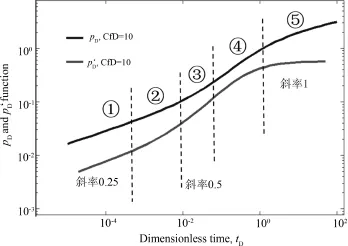
图5 低导流裂缝压力Fig.5 Pressure of low conductive fracture

3 实例计算与参数敏感性分析

3.1 实例计算

选取大庆长垣外围致密油区块，部分试验区采用压裂水平井开采，选取典型致密油藏试验区域进行实例计算，压裂水平井微地震监测如图6所示，油层厚度为3.2m，原始地层压力18MPa，井底流压9MPa，基质渗透率为0.23×10－3μm2，原油密度0.826g·cm－3，原油体积系数为1.052，原油粘度为1.45mPa·s，有效水平井长度为1 400m，压裂16段，每段压2－3簇缝，人工裂缝平均半长为154m，井筒半径0.05m.计算其无因次压降曲线与实际动态数据对比如图7所示，计算结果能够拟合实际数据点.

图6 压裂水平井微地震监测图Fig.6 Micro⁃seismicmap of fractured horizontalwell

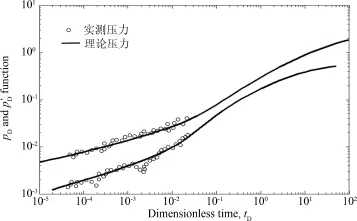
图7 压力拟合Fig.7 Pressure fitting

3.2 储层各向异性对压力动态的影响

储层各向异性对压力动态的影响在以往的研究中只是反映在渗透率主值上［16－17］，无因次压降分布如图8所示，对于实际地层，最大渗透率方向与井筒呈一定角度，而角度的大小对压力动态和产能影响较大，如图9所示，渗透率主值方向与人工裂缝垂直时无因次压降最小，定井底流压产量最大，随着渗透率主值方向与人工裂缝角度的减小，产量减小.因为，裂缝半长很大，垂直裂缝面的渗流区域很大，而平行裂缝方向流入裂缝的流量所占比例较小.

3.3 裂缝条数对压力动态的影响

随着压裂工艺技术的不断完善和提高，多裂缝压裂水平井得到了广泛的应用，特别是针对非常规油藏的开发与增产.如图10所示：人工裂缝条数对压力动态影响很大，随着裂缝条数的增加，同样的生产时间时，无因次压降变小.这是由于增加裂缝的条数可以使流体更多的流入井筒中，从而减少了渗流阻力.但是随着裂缝条数的继续增加及生产时间的增加，这种变化会越来越不明显.虽然裂缝条数增加能提高水平井产能，但随着裂缝的增加，产能的增加幅度会减小.

图8 渗透率主值方向与人工裂缝存在夹角Fig.8 Pressure distribution of different angles between permeabilitymain principal value and fractures

图9 渗透率主值与裂缝的角度压力Fig.9 Pressure of different angles between permeability main principal value and fractures

3.4 裂缝半长对压力动态的影响

裂缝半长是影响压裂水平井生产动态的又一个重要因素.裂缝半长对产能有直接的影响，通过对比不同裂缝半长对应井底压力曲线如图11所示，可以看出，随着裂缝长度的增加，无因次压降变小，但这种变小并不是无限制的，随着裂缝半长的增加，无因次压降减小的幅度变小.

图10 不同裂缝条数井底压力Fig.10 Pressure distribution of different number of fractures

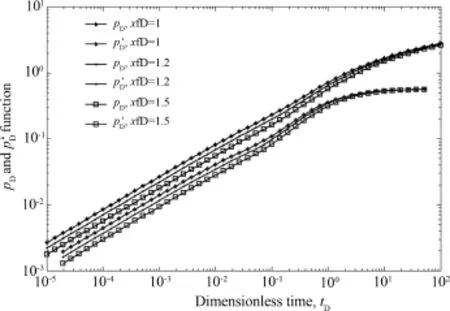
图11 不同裂缝半长井底压力Fig.11 Pressure distribution of different fractures half length

3.5 裂缝导流能力对压力动态的影响

裂缝导流能力的大小直接影响到压裂水平井最终的产能，通过对比不同裂缝导流能力对应井底压力曲线的影响如图12所示，可以看出，裂缝导流能力越大，无因次压降越小，但随着裂缝导流能力的增加，无因次压降减小的程度变小，特别是当无因次导流能力达到上百数量级后，产能增加幅度很小.

3.6 裂缝角度对压力动态的影响

目前对裂缝与井筒角度对压力和产能的影响研究较少，通过分析不同裂缝与井筒夹角井底压力如图13所示，裂缝与井筒夹角越大，无因次压降越小，对应产能越大，当裂缝与井筒垂直时，产能达到最大值.通过对比不同裂缝与井筒夹角井底压力图还可发现，角度对产能的影响不如前面几个因素明显，对产能的影响程度小于裂缝数目，半长等.

4 结论

1）结合各向异性油藏渗透率张量模型以及偏微分方程变换将各向异性油藏转化为各向同性油藏，形成了相应渗透率和空间位置表征，为建立渗流方程提供基础.

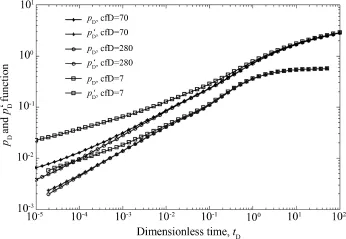
图12 不同裂缝导流能力井底压力Fig.12 Pressure distribution of different fracture conductivity

图13 不同裂缝与井筒夹角井底压力Fig.13 Pressure distribution between different angles of fractures and wellbore

2）基于格林函数，结合有限元一维单元插值函数，建立裂缝流动单元的数学表征，推导裂缝单元之间的流动关系，耦合地层向裂缝流动和裂缝内流动方程，得到任意角度多裂缝压裂水平井定产条件下的井底压力.

3）计算结果与已有解析结果对比，压力曲线以及压力导数曲线几乎相同，验证模型的可靠性与准确性.

4）分析多裂缝压裂水平井压力特征，存在压裂裂缝线性流、地层线性流、系统径向流3种流动形态，通过参数敏感性分析发现，压裂裂缝条数越多，相同的生产时间，无因次井底压降越小；裂缝条数对流动影响明显，但随着压裂条数的增加，压降变化幅度减小；裂缝长度和导流能力也有相似的变化.

5）对比地层最大渗透率方向与人工裂缝与井筒呈不同角度的情况，得出：人工裂缝与井筒角度越大，产能越大，当裂缝垂直于井筒时，产量最大，但角度影响程度不及裂缝长度、导流能力，地层最大渗透率方向垂直于人工裂缝时，产量最大，因此，当人工裂缝垂直于井筒，并同时垂直于地层最大渗透率方向时，达到最大产量.

［1］ Yao Jun，Sun Hai，Fan Dongmei，et al.Transportmechanisms and numerical simulation of shale gas reservoirs［J］.Journal of China University of Petroleum，2013，37（1）：91－98.

［2］ Huang Yanzhang.Flow mechanism of low permeability reservoirs［M］.Beijing：Petroleum Industry Press，1998：58－79.

［3］ Gringarten A C，Ramey H J.The use of source and green functions in solving unsteady⁃flow problems in reservoirs［R］.SPE 3818，1973.

［4］ Gringarten A C，Ramey H J.Unsteady⁃state pressure distributions created by a well with a single horizontal fracture，partial penetration，or restricted entry［R］.SPE 3819，1974.

［5］ Guo G，Evans R D.Pressure⁃transient behavior and inflow performance of horizontalwells intersecting discrete fractures［R］. SPE 26446，1993.

［6］ Al Rbeawi，Djebbar T.Transient pressure analysis of a horizontal well with multiple inclined hydraulic fractures using type⁃curvematching［R］.SPE 149902，2012.

［7］ Valko P，Amini S.The method of distributed volumetric sources for calculating the transient and pseudosteady⁃state productivity of complex well⁃fracture configurations［R］.SPE 106279，2007.

［8］ Amini S，ValkóP.Using distributed volumetric sources to predict production from multiple⁃fractured horizontal wells under non⁃Darcy⁃flow conditions［R］.SPE 120110，2010.

［9］ Zhu D，Magalhaes F V.Predicting the productivity ofmultiple⁃fractured horizontal gas wells［R］.SPE 106280，2007.

［10］ Ozkan E，Raghavan R.Some new solutions to solve problems in well testanalysis：Part1⁃Analytical considerations［R］.SPE，1998.

［11］ Ozkan E，Raghavan R.Supplement to new solutions for well⁃test⁃analysis problems：Part 1⁃Analytical considerations［R］. SPE，1991.

［12］ Ozkan E，Raghavan R.New solutions for well⁃test⁃analysis problems：Part 1⁃Analytical considerations（includes associated papers 28666 and 29213）［R］.SPE 18615，1991.

［13］ Raghavan R S，Chen C，Agarwal B.An analysis of horizontalwells intercepted bymultiple fractures［R］.SPE 27652，1997. ［14］ Brown M，Ozkan E，Raghavan R.Practical solutions for pressure⁃transient responses of fractured horizontal wells in unconventional shale reservoirs［R］.SPE 125043，2010.

［15］ Ozkan E，Brown M L，Raghavan R.Comparison of fractured⁃horizontal⁃well performance in tight sand and shale reservoirs ［R］.SPE 121290，2010.

［16］ Liu Yuetian，Zhang Jichang.Stable permeating flow and productivity analysis for anisotropic reservoirs in horizontal wellnetworks［J］.Petroleum Exploration and Development，2004，31（1）：94－96.

［17］ He Yinfu，Yin Hongjun，Yang Zhengming，et al.Boundary elementmethod for unstable flow in uniform anisotropic reservoir ［J］.Daqing Petroleum Exploration and Development，2006，25（5）：37－40.

［18］ Yao Jun，Li Yaqin，Huang Chaoqin.Finite flement simulation of anisotropic reservoir considering full permeability tensor［J］. Journal ofWuhan Polytechnic University，2009，28（3）：1－6.

［19］ Lian Peiqing，Cheng Linsong，Cao Renyi，et al.A coupling model of low permeability reservoir and fractured horizontal wellbore in nonsteady state［J］.Chinese Journal of Computational Physics，2010，27（2）：203－209.

［20］ Tong Dengke，Chen Yinlei.A note on Stehfestmethond on Laplace numerical inversion［J］.Acta Petrolei Sinica，2001，22 （6）：91－92.

［21］ Blasingame T A，Poe B D.Semi⁃analytic solutions for a well with a single finite⁃conductivity vertical fracture［R］.SPE 26424，1993.

Linear Element M ethod for M ulti⁃angle Fractured Horizontal W ell in Anisotropic Reservoir

FANG Sidong1，CHENG Linsong1，XIN Yinan1，HE Congge2
（1.College of Petroleum Engineering，China University of Petroleum（Beijing），Beijing 102249，China；
2.Research Institute ofPetroleum Exploration and Development，PetroChina，Beijing 100083，China）

With Green function and Laplace transformation，one⁃dimensional element is established considering effectof permeability tensor of anisotropic reservoir.Inflow of fracture is obtained by linear interpolation of endpoints and flow in fracture is treated with linear integral of flow rate.Coupling flow in formation and fractures，calculating method for bottom⁃hole pressure is formed semi⁃analytically.It shows that there are three flow regimes including fracturing linear flow，formation linear flow and system radial flow. Themore the fractures，the less the dimensionless pressure and number of factures has significant impacton flow rate.With increase of fractures increasing rate is dropping in the same time.Fracture length and conductivity have similar characteristics.Flow rate is improving as angle between fracture and wellbore is increasing.Flow rate reachesmaximum as fracture is perpendicular to wellbore，and vice versa.Angle between maximum permeability and fracture has similar impact on production.In summary，production rate reach maximum as fracture is perpendicular to wellbore and direction ofmaximum permeability.

anisotropic reservoir；fractured horizontalwell；well test；source function；multi⁃angle fractures

TE312

A

2014－09－13；

2014－12－11

国家自然科学基金（51174215/E0403）资助项目

方思冬（1988－），男，在读博士，主要从事低渗透油藏工程和数值模拟研究，E⁃mail：jbwolfgang＠163.com

Received date： 2014－09－13；Revised date： 2014－12－11