二维非均匀多孔介质中不可压两相驱替的有限分析算法
郑晓磊,刘志峰,王晓宏,施安峰
(中国科学技术大学热科学和能源工程系,安徽合肥 230026)
文章编号:1001⁃246X(2015)05⁃0586⁃09
二维非均匀多孔介质中不可压两相驱替的有限分析算法
郑晓磊,刘志峰,王晓宏,施安峰
(中国科学技术大学热科学和能源工程系,安徽合肥 230026)
为提高油藏数值模拟算法的计算效率,在求解单向稳态渗流的有限分析算法基础上,构建二维非均匀多孔介质中不可压两相渗流的有限分析算法.算法中,网格界面上的平均渗透率不是简单地取为相邻网格渗透率的调和平均值,而是通过奇点邻域解析解积分求得.相比于传统的数值算法,有限分析算法随着网格的加密,能够很快地收敛(仅需将原始网格细分至2×2或3×3),并且其计算精度和收敛性不依赖于介质的非均匀强度,从而计算效率得到提高.
有限分析算法;多相流动;多孔介质;非均匀介质;多尺度模拟
0 引言
多孔介质中的多相流动在很多科学和工程领域广泛存在,比如石油开采工业中常见的水驱油和蒸汽驱油等.其它的例子还包括干燥过程、多相流化床反应器,热管中的二元混合物流动、以及地热储能中的盐水混合物流动等等.多相流问题的强非线性使得理论分析异常困难,从而数值模拟成为研究相关问题的必要手段.以石油工业为例,在实践中广泛使用的油藏数值模拟技术主要用于预测储层性能,比较各种采收方案,以及测试不同的运营策略等等,其目的是实现企业利润的最大化.出于这个原因,已经有大量发展较为成熟的数值算法在实际中运用[1],如联立求解法(SS)和隐式压力-显示饱和度解法(IMPES)[2].SS方法[3-4]是把油相和水相压力作为直接的待求变量求解,而饱和度则作为毛管力的函数,根据毛管力得到饱和度.IMPES方法[5]的最基本思想是假定毛管力梯度在每个时间步里是不变的,利用描述多相流动的方程组得到其中某一相的压力方程,隐式求解该压力方程从而进一步去更新每个时间步内的饱和度值.如果不假定毛管力梯度在每个时间步里是定值,饱和度将隐式求解,就可以得到一种全隐式的方法—顺序求解法(SEQ)[2].
在以上提到的诸方法中,网格节点间的绝对渗透率通常都定义为相邻网格绝对渗透率的调和平均值,相对渗透率则由上游节点的饱和度确定[2].众所周知,在非均匀性很强的情况下,调和平均算法会严重低估网格间的界面流量.Cordazzo给出了一个4×4的单相流动算例,如采用调和平均算法,需要将原始网格细分至700×700的密网格,其计算结果才能与真值相近[6-7].Romeu和Noetinger建立了一种理论分析方法来研究等效渗透率计算的准确性.他们证实了传统格式的计算结果会存在很大偏差,而且随着网格的加密,其向真值的收敛速度很慢.简言之,对于非均匀性很强的介质,传统格式如果没有进行足够地加密,计算结果会导致很大的误差[8].
实验研究方面,Dave研究了渗透率或润湿性存在差异的2×2方型多孔区域中的多相流动问题[9].实验结果表明,即使渗透率很小的差异也会导致流线很大的弯曲.流体从四个象限的中心角点处快速通过形成“窜流”.“窜流”现象导致流线弯曲,从而保持流动在高渗透率区域之间进行,并且在角点区域形成一个很大的压力梯度.Dave认为,如何用少量的网格模拟出窜流现象,对于传统数值算法是一个很大的挑战.
在国内,杨权一等提出了在渗透率间断附近的自适应加密算法[10];段志田等提出了改进的两相渗流有限元数值算法[11];林刚等利用萨曼斯基技巧改造牛顿迭代方法[12];梁栋根据混溶和不混溶情况,分别提出了相应的粘性分离算法和迎风算法[13];这些方法在一定程度上有效地提高了两相渗流的计算效率和精度.
已经知道,对于二维单相流动,在不同渗透率区域交界的角点附近,压力呈幂律分布,而且其梯度是发散的.这个特殊的规律是导致传统格式计算效果差的原因.为了提高计算效率,在角点幂律解析解的基础上,提出了针对单向流动的有限分析算法[14-15].该算法在2×2或3×3的网格细分条件下,就可以得到相当准确的计算结果,并且其准确性和收敛速度不依赖于介质的非均匀强度.本文针对二维不可压缩两相流动,进一步构造相应的有限分析算法.
1 二维不可压两相流动中的有限分析算法
二维不可压油水两相流动的控制方程可表述为

其中ϕ表示孔隙度;sα表示相饱和度,下标α表示水相或者油相;Vα表示各相的速度;k是多孔介质的绝对渗透率,本文作为标量处理;krα表示α相的相对渗透率,它是饱和度sα的函数;μα是α相的粘度系数;Pα是α相的压力;毛管力Pc是两相压力之间的差值,也是饱和度的函数.将(1)式的前两个方程相加,并利用sw+so=1可以得到


图1 方程(2)的离散示意图,阴影部分表示点P0的影响区域Fig.1 Sketch map of discretization of Eq.(2)on a square cell in 2D case,where the hatched area represents influenced area of grid node P0

本文重点阐述用有限分析方法[16]来数值求解压力方程(2).对控制容积(见图1)应用流量守恒,可以得到其中Q(pqi+1/2,j+1/2)表示穿过控制体相应边界的总流量(包括水相和油相),下标pq表示如果以(i+1/2,j+1/2)为坐标原点,流量是从第p象限流向第q象限.根据方程(2),(3)中的每个Q可以分成两个部分:Qpw和Qp,分别对应方程(2)中的-(krw/μw+kro/μo)kΔPw和-krok/μoΔPc,因此方程(3)又可以改写成
c

有限分析法的关键就是如何计算界面流量(Qp和Qp).各界面流量由相应的奇点(i+1/2,j+1/2)区域决
wc定,根据奇点区域性质不同,分为两种情况:①角域压力呈幂律分布(ki,jki+1,j+1≠ki+1,jki,j+1);②角域压力呈线性分布(ki,jki+1,j+1= ki+1,jki,j+1).
1.1 角域压力呈幂律分布(ki,jki+1,j+1≠ki+1,jki,j+1)
如图1阴影部分所示,绝对渗透率k在四个网格内有不同的值ki,j,ki+1,j,ki,j+1和ki+1,j+1,和单相流动一样,压力梯度在网格公共点P0附近是发散的[14-15].该奇点邻域(图2中的小圆)的解析解是有限分析法的核心.对于方程(2),由于奇点附近的饱和度分布无法确定,所以找不到严格的奇点邻域解析解.如果考虑到流动的非定常性,情况将更加复杂.因此,首先要简化方程(2),以得到近似的奇点邻域解析解.
记奇点处的水相饱和度值为s∗,大多数情况下,水相饱和度在奇点附近是连续的;仅当饱和度锋面恰通过该点时才不连续.事实上,饱和度锋面会在迅速通过该奇点,对tn到tn+1这个时段所造成的影响可以忽略.因此,总可以假定饱和度在奇点附近连续,其梯度是个有限值,故与发散的压力梯度ΔPw相比,方程(2)中的kkro/μoΔPc可以忽略,故方程(2)可以简化为

在实际计算中,为保证物理上的正确性,离散的(krw/μw+kro/μo)值总是采用“迎风格式”,即定义在上游,故在角域,方程(5)中(krw/μw+kro/μo)项可视为常数.也就是说,可以把类拉普拉斯方程(6)在奇点邻域的解析解作为方程(2)一个合理近似.

根据上文分析,在ki,jki+1,j+1≠ki+1,jki,j+1的情况下,方程(4)中的界面流量(Qpc)21,(Qpc)34,(Qpc)41和(Qpc)32可以忽略;界面流量Qpw和离散的水相压力之间的关系,可以根据方程(6)的奇点邻域解析解来建立.把ki+1,j+1,ki,j+1,ki,j,ki+1,j,(Pw)i+1,j+1,(Pw)i,j+1,(Pw)i,j,(Pw)i+1,j,si+1,j+1,si,j+1,si,j,si+1,j(见图2)相应地简记为k1,k2,k3,k4,P1,P2,P3,P4,s1,s2,s3,s4(见图3).界面流量Qpw和离散的水相压力之间的关系可以写成[11]
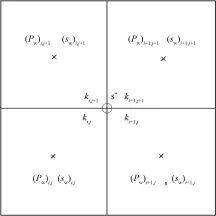
图2 方网格下计算节点示意图Fig.2 Plot of grid node in a rectangular grid system

图3 受奇点P0控制的界面流量Qpw和Qpw示意图Fige.3 Plot of interface fluxes Qpwand Qpcdominated by a grid node

上述公式的详细推导参见文献[10]或[11].
1.2 角域压力呈线性分布(ki,jki+1,j+1=ki+1,jki,j+1)
ki,jki+1,j+1=ki+1,jki,j+1的情况主要发生在网格加密过程中,这种情况下,压力梯度ΔPw和毛管力梯度ΔPc在网格节点附近都是有限值.因此,-kkro/μoΔPc这部分不能够忽略,方程(2)在此情况下的离散格式将退化到传统形式[11].方程(4)中的界面流量Qpw和Qpc可以写成
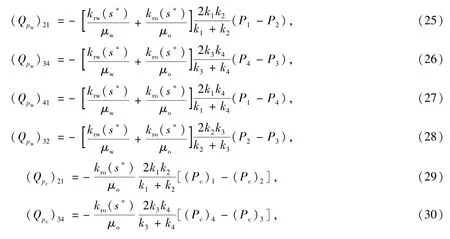
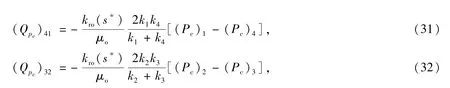
其中(Pc)1=Pc(s1),(Pc)2=Pc(s2),(Pc)3=Pc(s3),(Pc)4=Pc(s4).
至此,可以简述利用有限分析法求解二维不可压缩两相流动方程(1)的步骤如下.这里,有限分析算法也可以看作是改进的IMPES方法.
1)将tn时刻饱和度场的离散值作为tn+1时刻的迭代初值,即:,其中表示tn时刻饱和度场的离散值,表示tn+1时刻的第k次迭代值.

其中Qw表示穿过控制体边界的水相流量,与-krwk/μwΔPw相对应(见图3),由于Qpw与-(krw/μw+kro/μo)k ΔPw对应,所以Qw和Qpw之间存在一个简单的关系:
事实上,Qpw在步骤2)中已经求出,所以Qw可以直接得到.求解方程(33)可以得到tn+1时刻第k+1次的迭代值.
4)更新得到tn+1时刻离散饱和度场的第k+1次迭代值.重复步骤2)和3),直到得到收敛的.

2 数值算例
2.1 渗透率棋盘式分布算例
如图4所示的二维棋盘式结构在理论和数值上都引起研究者们的广泛兴趣,经常被用来检验一个数值算法的准确性.本文考虑9×9的方网格系统,分别用有限分析法和IMPES方法计算不同的k2/k1情况下活塞型驱替算例.为了得到更准确的结果,每一个原始网格被细分至n×n的计算网格.分别给出了k2/k1=10,100,1 000情况下有限分析法和传统IMPES方法的计算结果,以作比较.
设定棋盘式结构中的无量纲绝对渗透率分别为k1=0.1,1,10和k2=100,对应k2/k1=10,100,1 000的情况;进出口的无量纲水相压力和无量纲饱和度设为:Pin=3.0,sw in=1.0和Pout=1.0,swout=0.3;相对渗透率率曲线取为:krw=/(2-)和kro=2(1-)/(2-);无量纲粘度设为μw=1和μo=2.这种情况下,分流量函数f(sw)=(krw/μw)/(krw/μw+kro/μo) =.此时f″(sw)≥0,所以流动属于活塞式驱替[17].

图4 二维棋盘式分布示意图Fig.4 A sketchmap of 2D checkerboard problem
图5~7给出了k2/k1=10、k2/k1=100及k2/k1=1 000情况下有限分析法和传统IMPES方法在不同的加密参数n下,计算出的饱和度场分布.可以看出,k2/k1=10情况下,非均匀性不是很强,有限分析法和IMPES方法都收敛的较快,有限分析法的锋面移动速度略快于IMPES;随着非均匀性增强,k2/k1=100和1 000时,随着网格细分参数n的增加,有限分析法收敛的速度比传统IMPES方法要快得多,有限分析法的计算结果在n=8和n=16时已基本没有区别;而对于传统IMPES方法,n=8和n=16的计算结果都非常不准确,与有限分析法相比,传统IMEPS方法严重低估了锋面的移动速度.为了能达到和有限分析法相近的准确度,IMPES方法需要将计算网格划分得非常密,从而需要很大的计算成本,以至不可行.换言之,有限分析方法则可以在较粗的计算网格条件下获得很高的准确度,而且不依赖介质的非均匀强度.

图5 k2/k1=10情况下FAM和传统IMPES方法在不同的网格加密参数n下计算的水相饱和度场Fig.5 Saturation fields of a 2D checkerboard calculated with FAM and traditional IMPES under different grid refinement parameter n as k2/k1=10
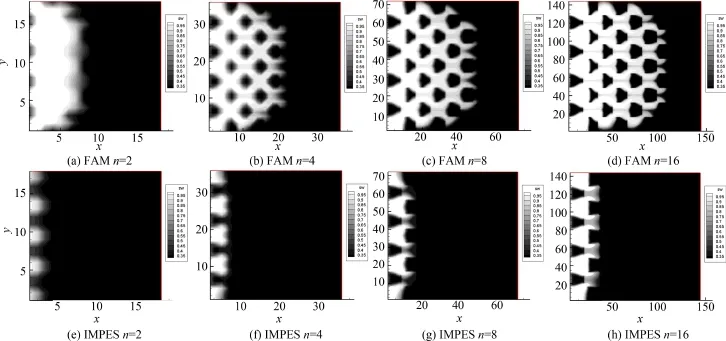
图6 k2/k1=100情况下FAM和传统IMPES方法在不同的网格加密参数n下计算的水相饱和度Fig.6 Saturation fields of a 2D checkerboard calculated with FAM and traditional IMPES under different grid refinement parameter n as k2/k1=100

图7 k2/k1=1 000情况下FAM和传统IMPES方法在不同的网格加密参数n下计算的水相饱和度Fig.7 Saturation fields of a 2D checkerboard calculated with FAM and traditional IMPES under different grid refinement parameter n as k2/k1=1 000
图8给出了k2/k1=10,100,1 000的情况下有限分析法和传统IMPES方法计算得到的出口边界见水时间.这里定义出口边界见水时间为出口边界任意位置出现水相饱和度大于0.35的情况.如图8所示,随着介质非均匀性的增强,在不同的网格加密条件下,有限分析法计算的见水时间几乎是不变的,而对传统IMPES方法,随着网格的加密,计算的见水时间会逐渐减短,而且随着介质非均匀性增强,收敛越来越困难,甚至无法收敛,这也就意味着传统IMPES方法在粗网格情况下会严重低估见水时间.
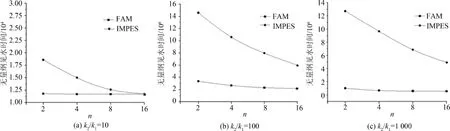
图8 不同k2/k1情况下FAM和传统IMPES方法计算的无量纲见水时间随着网格加密参数n的变化Fig.8 Water breakthrough time of a 2D checkerboard calculated with FAM and traditional IMPESunder different grid refinement parameter n as k2/k1=10,100,1 000
2.2 渗透率对数正态分布(Log⁃normal)算例
地层中的渗透率常满足对数正态分布,它的概率密度函数为

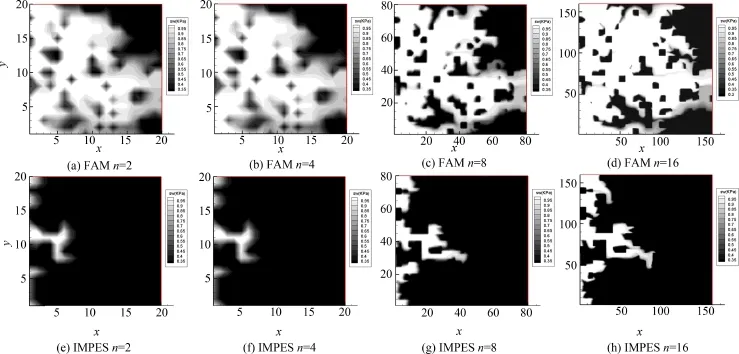
图9 Log⁃normal分布情况下FAM和传统IMPES方法在不同的网格加密参数n下计算的水相饱和度场Fig.9 Saturation fields calculated with FAM and traditional IMPESmethod under different grid refinement parameter n for the case of lognormally distributed permeability
从图中可以看出,渗透率对数正态分布情况下,传统IMPES方法依然严重低估了见水时间,且随着网格加密,计算值收敛得很慢;而有限分析法即使在粗网格情况下也能计算出相对准确的饱和度场,且见水时间在粗网格条件下也收敛.这个算例再一次证实了有限分析算法的高效性.
3 结论和讨论
针对二维非均匀多孔介质中的不可压两相流动,提出一种有限分析算法.当四个相邻网格的绝对渗透率满足ki,jki+1,j+1≠ki+1,jki,j+1时,水相和油相压力梯度在网格奇点处是发散的,而毛管力梯度是有限值.因此毛管力梯度在奇点邻域可以忽略,类拉普拉斯方程(6)在奇点邻域的幂律解析解可以作为两相流动的一个近似解,并可以基于此构造有限分析格式.而对于ki,jki+1,j+1=ki+1,jki,j+1的情况,相压力梯度和毛管力梯度都是有限值,这时的数值格式自动退化为传统形式.

图10 Log⁃noram l情况下FAM和传统IMPES方法计算的无量纲见水时间随着网格加密参数n的变化Fig.10 Water breakthrough time calculated with FAM and traditional IMPESmethod under different grid refinement parameter n for the case of lognormally distributed permeability
和传统数值算法相比,有限分析法在网格加密过程中,有更快的收敛速度,且不依赖于介质的非均匀强度.相反的,如果用传统的数值算法去求解,为得到相对准确的结果,往往需要对原始网格进行大幅度加密.
另一个问题是关于多相流粗化.从本文的数值模拟结果来看,锋面几乎处处存在,饱和度场出现波动式分布(见图5和8).此时,如果将9×9的网格合并成一个粗网格,并定义一个等效饱和度值来替代该区域内的波动饱和度场,这种做法可能并不合适.换言之,如果用等效饱和度值来计算粗化后网格间的各相流量,可能会带来相当大的误差.
[1] Allen M B.Numericalmodeling ofmultiphase flow in porousmedia[J].Adv Water Resource,1995,8:162-187.
[2] Aziz K,Setttari A.Petroleum reservoir simulation[M].Applied Science,1979.
[3] Breitenbach E A,Thurnau D H,van Poolen H K.Solution of the immiscible fluid flow simulation equation[J].Society of Petroleum Engineers Journal,1969:155-169.
[4] Chen C J,Chen H C.Finite analytic numericalmethod for unsteady two⁃dimensional Navier⁃Stokes equations[J].JComput Phys,1984,53:209-226.
[5] Coats K H,Nielsen R L,Terhune M H,Weber A G.Simulation of three⁃dimensional two⁃phase flow in oil and gas reservoirs [J].Society of Petroleum Engineers Journal,1967:377-388.
[6] Cordazzo J,Maliska C R,Romeu R K.A Considerations about the internodal permeability evaluation in reservoir simulation [C].The 2nd Brazilian Congress on R&D in Petroleum and Gas,Rio de Janeiro,June,15-18,2003.
[7] Cordazzo J,Hurtado F SV,Maliska C R,Da Silva A F C.Numerical techniques for solving partial computationalmethods in engineering[C].2003.
[8] Dawe R A,Grattoni C A.Experimental displacement patterns in a 2×2 quadrant block with permeability and wettability heterogeneities—problems for numericalmodeling[J].Trans Porous Media,2008,71:5-22.
[9] Douglas J J,Peaceman D W,Jr Rachford H H.A method for calculating multidimensional immiscible displacement[J]. Metallurgical and Petroleum Engineers,1959,216:297-306.
[10] Yang Q Y,Liu F P,Yang C C,Liu L F,Zhuo L.Adaptive nonuniform grid upscalingmethod of three⁃dimensional transient heterogeneous fluids in porousmedia[J].Chinese JComput Phys,2003,20:193-198.
[11] Duan Z T,Zhang D M.Finite element algorithms for simulating water flow in variably saturated porousmedia[J].Chinese J Comput Phys,1992,9:15-22.
[12] Lin G,Shi JM,Lin C B,Lv T,Lin A M.Gas reservoirs simulation and numerical comparison of results[J].JComput Phys,1991,8:286-278.
[13] Liang D.New numericalmethods and their theoretical analysis for the two phase displacement problems[J].JComput Phys,1992,9:286-525.
[14] Liu Z F,Wang X H.Finite analytic numericalmethod for two⁃dimensional fluid flow in heterogeneous porous media[J].J Comput Phys,2013,235:286-301.
[15] Qu Z X,Liu Z F,Wang X H,Zhao P.Finite analytic numericalmethod for solving two⁃dimensional quasi⁃Laplace equation [J].Numerical Methods for Partial Differential Equations,2014,DOI 10.1002/num.21863.
[16] Romeu R K,Noetinger B.Calculation of internodal transmissibilities in finite differencemodels of flow in heterogeneous porous media[J].Water Resour Res,1995,31:943-959.
[17] Wu B,Liu Z F,Wang X H.A study on the numerical algorithm for the non⁃piston⁃like displacement in oil⁃water two⁃phase flows[J].Journal On Numerical Methods and Computer Applications,2012,33:274-282.
Finite Analytic Numerical M ethod for Two⁃Phase Incom pressible Flow in 2D Heterogeneous Porous M edia
ZHENG Xiaolei,LIU Zhifeng,WANG Xiaohong,SHIAnfeng
(Department of Thermal Science and Energy Engineering,University ofScience and Technology of China,Hefei,Anhui 230026,China)
A finite analytic numerical scheme is constructed for two⁃dimensional two⁃phase flow in heterogeneous porous media. Compared with traditional numerical methods,FAM makes convergence faster as refinement parameter increases,and accuracy is independentwith heterogeneity.In contrast,as using traditional numerical schemes to simulate flow through a strong heterogeneous porousmedium,refinement ratio for grid cell needs to increase dramatically to get an accurate result.Compared with the proposed scheme,traditional numerical scheme underestimates greatly breakthrough time under coarse grids.However,to get a saturation distribution with high resolution even employing the proposed scheme,relative fine grids are still needed.This is different from FAM for solving a single phase flow,where coarse grids provide rather accurate results.
finite analytic method;multi⁃phase flow;fluid flows in porousmedia;heterogeneousmedia;multi⁃scale simulation
O362
A
2014-12-04;
2015-01-22
国家自然科学基金(11172295,11202205),中国科学技术大学青年创新基金(WK2090130017))及CNPC⁃CAS科技合作资助项目
郑晓磊(1987-),男,安徽六安,博士生,从事油藏数值模拟研究,E⁃mail:lzf123@ustc.edu.cn
Received date: 2014-12-04;Revised date: 2015-01-22

