材料热物性与热源强度辨识的改进遗传算法

颜 帆，卢 玫

（上海理工大学能源与动力工程学院，上海 200093）

文章编号：1001⁃246X（2015）05⁃0623⁃08

材料热物性与热源强度辨识的改进遗传算法

颜 帆，卢 玫∗

（上海理工大学能源与动力工程学院，上海 200093）

建立二维非线性导热逆问题（IHCP）的数学模型.通过对基本遗传算法逐步改进得到三种不同改进阶段的遗传算法，分别用于反演导热问题中材料的导热系数及其内部热源强度，并比较遗传算法在各改进阶段用于求解导热逆问题时的收敛速度与求解精度，寻求一种使导热逆问题求解效率与计算精度更高的遗传算法改进策略.结果表明：提出的遗传算法改进策略达到了预期目的.

遗传算法；导热逆问题；导热系数；热源强度

0 引言

近年来导热逆问题（IHCP）在生物医学、无损探伤、电子芯片散热设计等领域运用愈发广泛.导热逆问题的求解通常可转化为一优化问题，由于其具有计算量大、不适定性和非线性等特点，因此选择一种合适、高效的优化方法对于解决此类反问题非常重要.不少文献采用传统梯度类优化方法，如正则化方法［1－2］、共轭梯度法［3－6］等求解导热逆问题，由于存在模型误差和观测误差，其解常常是振荡和不收敛的［7－8］，且依赖于初始搜索点［9－10］，当反演由单宗量向多宗量转变时，导热逆问题的不适定性和解的不唯一性表现地更加明显，计算量较单宗量反演时更大，故选择一个搜索能力强、鲁棒性好的优化方法是解决此类问题的有效手段.遗传算法作为一种智能优化算法，具有较强的全局与局部搜索能力和良好的鲁棒性，能较好地避免局部最优且不依赖于初始搜索点［11］，相比于传统寻优方法，其在非线性、多宗量辨识方面具有优势.国内外许多学者已将遗传算法运用于寻优过程，并有学者对遗传算法采取了一些改进措施.王登刚等人利用遗传算法反演材料导热系数时提出保留每代最优个体的策略［12］；王秀春等人对遗传算法目标函数标定过程进行改进［13］.乐恺等人针对所求问题目标函数具有多峰特征，提出了利用小生境技术提高遗传算法全局搜索能力［14］.杨伟超等人反演板坯温度时，考虑求解问题的特殊性，提出采用浮点数编码的遗传算法并由此采取针对浮点数编码的交叉与变异算子［15］.黄长清等人对铝板带热精轧轧制规程优化过程中，对遗传算法交叉、变异概率进行自适应改进［16］.Raudensky等人采用实数编码的遗传算法求解导热逆问题［17］.Liu为了提高遗传算法求解时的收敛速度与计算精度，将梯度寻优引入遗传算法中［18］.

借鉴上述遗传算法改进措施，通过在遗传算法中逐步引入价值函数，混沌序列以及择优选取子代等，分别建立三种处于不同改进阶段的遗传算法，并将其运用于反演材料热物性与热源强度的导热逆问题，旨在获得一种能提高导热逆问题求解效率与计算精度的改进遗传算法.

1 物理问题及数学描述

讨论物理对象如图1所示，截面形状为矩形，内部有一截面为点的热源，导热体的导热系数λ随温度T呈线性变化，并设为λ＝λ0＋aT.由于导热体长度尺寸远大于截面尺寸，因此，上述物理问题是一个二维非线性稳态导热问题，对应的控制方程及边界条件为

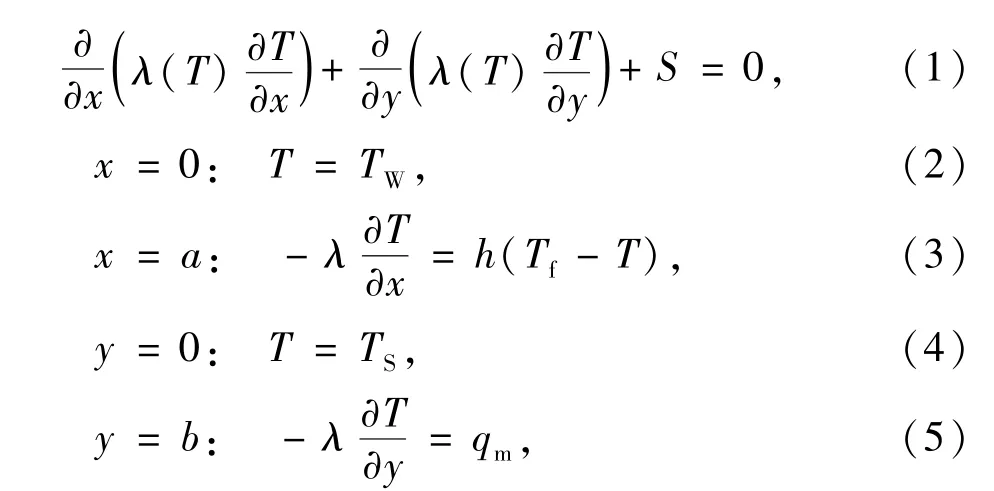
式中T为温度，K；λ为材料导热系数，W·（m·K）－1；S为热源强度，W·m－1；qm为热流密度，W·m－2；TS为南边界壁面温度，K；TW为西边界壁面温度，K；Tf为周围介质温度，K；h为表面对流换热系数，W·（m2·K）－1.

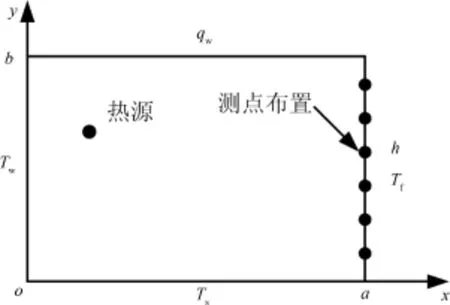
图1 计算区域示意图Fig.1 Schematic of calculation area

当材料导热系数、热源强度是待定参数时，上述导热问题即为导热逆问题，需要附加补充求解条件.本文通过在非第一类边界条件边界上布置若干测点（如图1所示），测量其温度值对导热逆问题进行反演求解［19］.定义补充求解条件

式中，Tm为测点处的实测温度向量.

式（1）、式（2）～（6）构成导热逆问题的数学描述.定义目标函数［20］

式中，n为测点个数，T为温度向量的计算值，它依赖于待识别的参数.

定义导热逆问题的解空间：0≤λ0≤999；0≤a≤0.1；0≤S≤999.利用遗传算法在解空间中随机产生一组解：λ0、a与S值，代入式（1）、式（2）～（5）所描述的导热正问题中求解其温度场，将对应测点处的计算温度向量代入式（7），目标函数越小则解越优，故而可转化为如式（8）所示一全局优化问题

2 遗传算法

遗传算法（genetic algorithm，GA）起源于对生物系统所进行的计算机模拟研究，由Holland教授在1967年首次提出.其基本思想是利用某种编码技术，将所求问题解空间中的可行解转化为称为染色体的数字串，通过选择、交叉、变异等遗传操作，使可行解逐渐改善，最终获得最优.

基本遗传算法可表示为

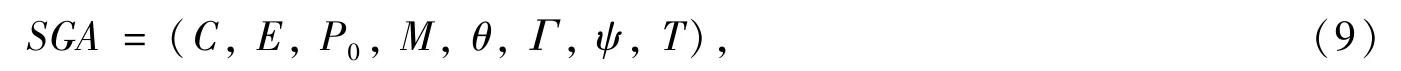
式中C表示个体编码方式；E表示个体适应度评价函数；P0表示初始种群，M表示种群大小，θ表示选择算子，Γ表示交叉算子，ψ表示变异算子，T表示算法终止条件.

基本遗传算法流程图如图2所示.

3 改进遗传算法

上述基本遗传算法对于导热反问题的求解仅是概率性收敛［12］.本文首先借鉴目前大多数学者已提出的遗传算法改进措施，对基本遗传算法作简单改进，得到GA⁃1.在GA⁃1的基础上引入价值函数得到GA⁃2.在GA⁃2的基础上再对其进行改进得到GA⁃3.具体操作过程如下.

GA⁃1：

1）采用实数编码；

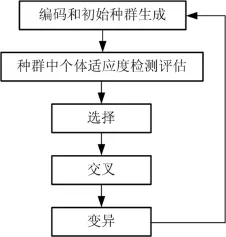
图2 遗传算法基本流程图Fig.2 Flowchart of GA

2）对由目标函数向适值函数的标定如式（10）：

式中F为适应度函数，f为个体目标函数，fmax与fmin依次为当前代中目标函数值最大与最小的个体，r为小于1的正实数.

3）变异方式上借鉴标准正态分布原理.本文只对被选中进行变异操作基因进行变异操作，以提高算法的局部搜索能力，加速算法的收敛，具体做法为：假设某代种群中一个体可表示为G＝（g1g2g3g4g5g6g7g8），且已选中该个体第三基因位上的基因g3进行变异操作，则其余基因位上基因值不变，第三基因位上基因值变为：＝g3＋N（0，1），式中N（0，1）表示服从标准正态分布的随机变量.

4）保留每代种群中最优个体.

GA⁃2：在GA⁃1基础上融入如式（11）的价值函数.

式中Jk（gij）表示第k代种群中第i个个体上第j位基因对应的价值函数，gij表示在该代种群中第i个个体上第j基因位上的基因，fij表示对应该个体的目标函数值.其基本思想是计算每代种群中所有个体相同基因位上基因的价值函数，根据这一基因位上基因的价值函数大小进行排序与重组种群.具体操作为：假设第k代种群中有且仅有三个个体，可表示为

若由式（11）计算得到J（g11）＝10，J（g21）＝14，J（g31）＝7，则根据这一基因位上基因的J值大小重组种群得到

第二位基因同理操作，直至最后一位基因.

GA⁃3：在GA⁃2基础上做如下改进.

1）将种群中个体基于价值函数重组操作置于选择操作之前.选择方式上采用基于种群中个体适应度值大小进行排序的方法，其基本思想为将种群中所有M个体按适应度值从小到大排序，则排序后第j个个体被选中的概率如式（12）所示.

2）交叉方式上采用择优交叉，每次交叉均进行N次，在2N个子代中选择适值最好的两个个体加入新一代种群；

3）交叉点与变异点的位置利用Logistic混沌序列产生的随机数来确定.假设第k代种群中两个体为

取初始值x（0）＝0.3，则x（1）＝4x（0）［1－x（0）］＝0.84，0.84×7＝5.88，取整得6，则第6位作为交叉点，保存此值作为以后确定交叉点的混沌迭代初值.变异操作同理.

三种改进算法在导热逆问题中求解流程如图3、4所示.

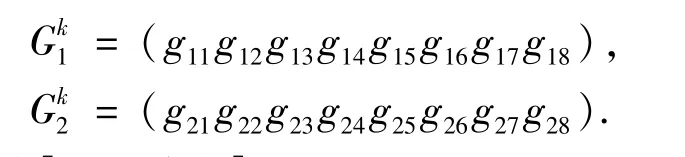
4 计算结果与分析

本文采用数值方法计算求解式（1）、式（2）～（5）所描述的导热正问题.首先采用有限体积法对图1所示计算区域进行离散，并引入边界条件，得到每个网格节点对应的离散方程，所有节点的离散方程构成一非线性方程组.计算中采用逐行法迭代求解方程组，直至收敛后得到整个计算区域的温度场.

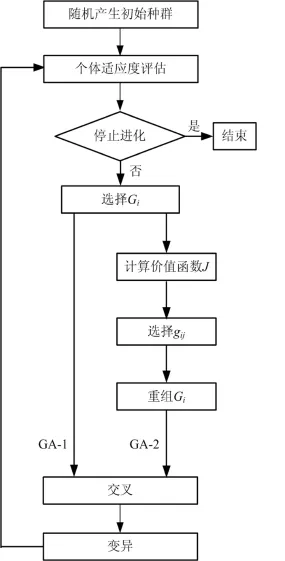
图3 GA⁃1与GA⁃2算法流程图Fig.3 Flowchart of GA⁃1 and GA⁃2

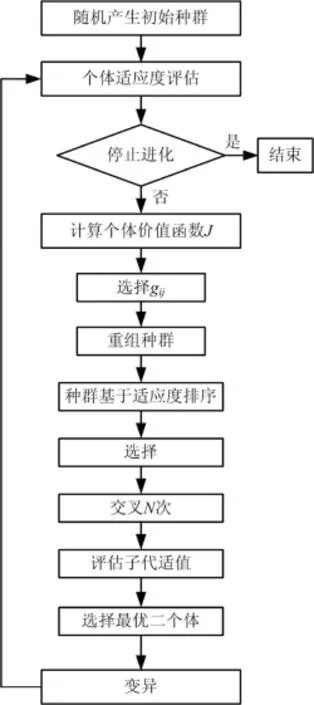
图4 GA⁃3算法流程图Fig.4 Flowchart of GA⁃3

计算时各参数取值如表1所示.假设该材料真实的导热系数λ＝500＋0.01T，热源强度S＝400W·m－1，代入式（1）、式（2）～（5）所示导热正问题中求解，得到整个计算区域的温度场，在边界处选取若干点温度值，用于代替实际测量值.

表1 各参数取值表Table 1 Values of parameters

4.1 三种改进遗传算法反演结果与分析

设定三种改进算法种群进化终止判据均为连续5代种群个体平均适应度之差绝对值小于0.01，同时对最大迭代次数设置限制，限定三种改进算法种群最大进化代数MG均为150，作为终止程序执行的准则.将以上三种算法分别运用于上述导热逆问题的反演求解，每种算法均进行3次反演计算，计算结果如表2所示.从表中可以看出，GA⁃3具有最好的求解效率与计算精度，GA⁃2其次.GA⁃3是在GA⁃2基础上，通过对选择、交叉等遗传操作的改进，更好地将优良基因传递至下一代，且采用混沌序列使得算法在初始反演阶段对解空间的全局搜索能力更强，在计算即将收敛阶段收敛速度更快，即算法的全局与局部搜索能力得到了提升.

表2中所列MGA算法是文献［14］中提出的改进遗传算法.由表中所列计算结果可以看出，仅作简单改进的GA⁃1，虽然克服了概率性收敛问题，但计算效率与精度低于MGA；GA⁃2虽然求解所需时间略长于MGA，但反演精度高于MGA；而本文最终获得的改进遗传算法GA⁃3，其计算效率与求解精度均明显优于MGA.

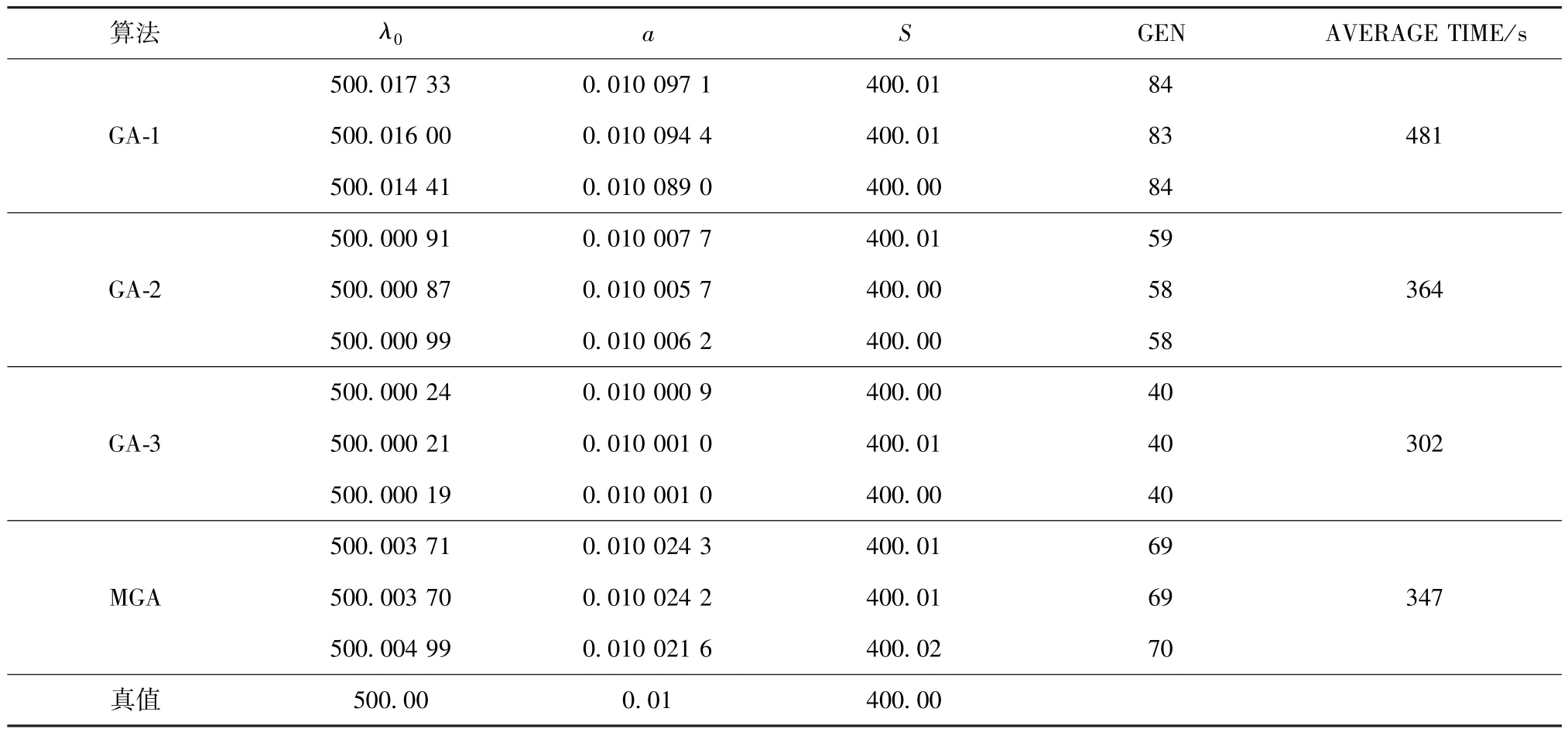
表2 计算结果Table 2 Calcu lation resu lts

为了解各算法在求解逆问题过程中种群进化趋势，限定三种改进遗传算法与MGA算法均进行90代种群进化，记录四种改进算法每代种群中最优个体目标函数值变化趋势，如图5.从图5可以看出，在种群进化代数相同的情况下，GA⁃3在反演计算中有着最高的求解精度.

GA⁃3中存在被选择父代进行N次交叉择优选择子代这一操作，对于正整数N的选取，文中进行了验证，结果如图6.图中ηN表示N取某正整数时程序运行时间的倒数.在达到几乎相同的求解精度情况下，从图中可知，N取4最优.

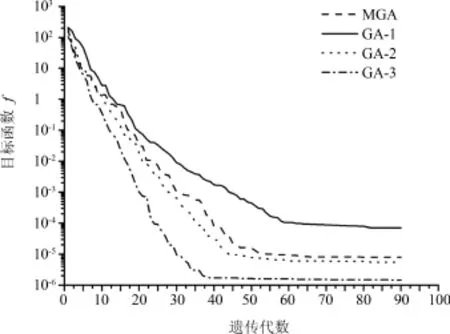
图5 种群中最优个体目标函数随代数的变化Fig.5 Objective functions of best individuals in population as functions of generations

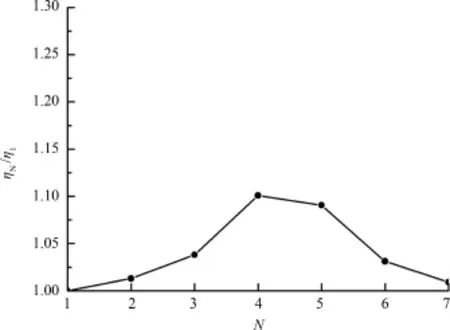
图6 求解效率随N取值变化Fig.6 Calculation efficiency as a function of N

4.2 随机噪声对算法反演结果的影响

对于以上导热逆问题的求解，测点温度是通过求解导热正问题模拟得到，为模拟测量误差对计算结果的影响，在没误差的正问题的精确解上施加随机噪声向量ε，如式（13），以检测算法在求解问题过程中的抗噪性能.

本文分别给予三种改进算法以3％、6％的随机噪声各自进行6次反演计算，用于模拟实际测量中出现的误差，所得结果如图7所示，取一次计算结果制成表3.从图7中可知GA⁃3抗噪声性能较GA⁃2稍好，GA⁃1抗噪声性能次于GA⁃2.

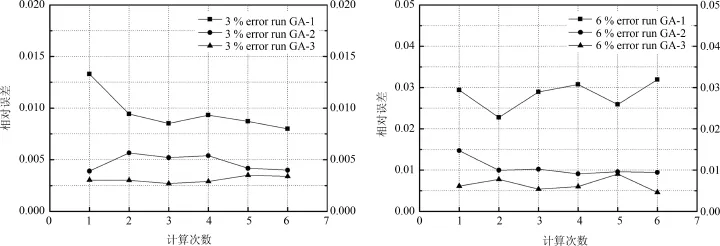
图7 输入噪声对计算结果的影响Fig.7 Influence of input noise on calculation results

表3 加入噪声反演结果Table 3 Calculation results under input noise

4.3 测点数量及分布对反演结果的影响

在测点布置与数量选择对导热逆问题反演结果的影响方面，参照图8，在计算区域东边界上均匀设置16个可选测点，在北边界靠近热源位置设置3个可选测点，图中均已标明序号.通过选择不同数量与位置处的测点，在不考虑噪声的情况下，采用GA⁃3算法对文中导热逆问题进行反演求解，结果如表4所示.

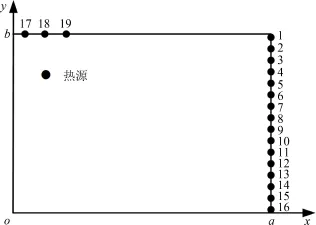
图8 测点编号示意图Fig.8 Serial number ofmeasuring points

从表4中可以看出，No.1选择东边界上3个测点进行反演计算，所得结果背离了真实值；采取No.5、No.6、No.7的测点数量与分布可反演得到正确的结果，反演精度接近一致且均比采取No.3、No.4时的反演精度要高；No.8有着最好的反演效率与精度.由表4可得出以下结论：（1）测点的布置应适当均匀且应达到一定的数量，同时测点数目并不是越多越好，过多的测点数目只会影响计算效率.（2）测点在数量选择上可从一个较小的数目开始，逐次递增，直至相邻两次计算结果在一个设定的允许范围之内，则倒数第二次测点数目为最小观测点数目.（3）对于文中导热逆问题，当材料内部存在线状轴向内热源且其位置已知，需要对其强度进行反演的情况下，在测点布置方面应尽可能使部分测点靠近热源均布，测点位置越接近热源，其上温度对热源强度的改变越敏感，越有利于结果的反演.

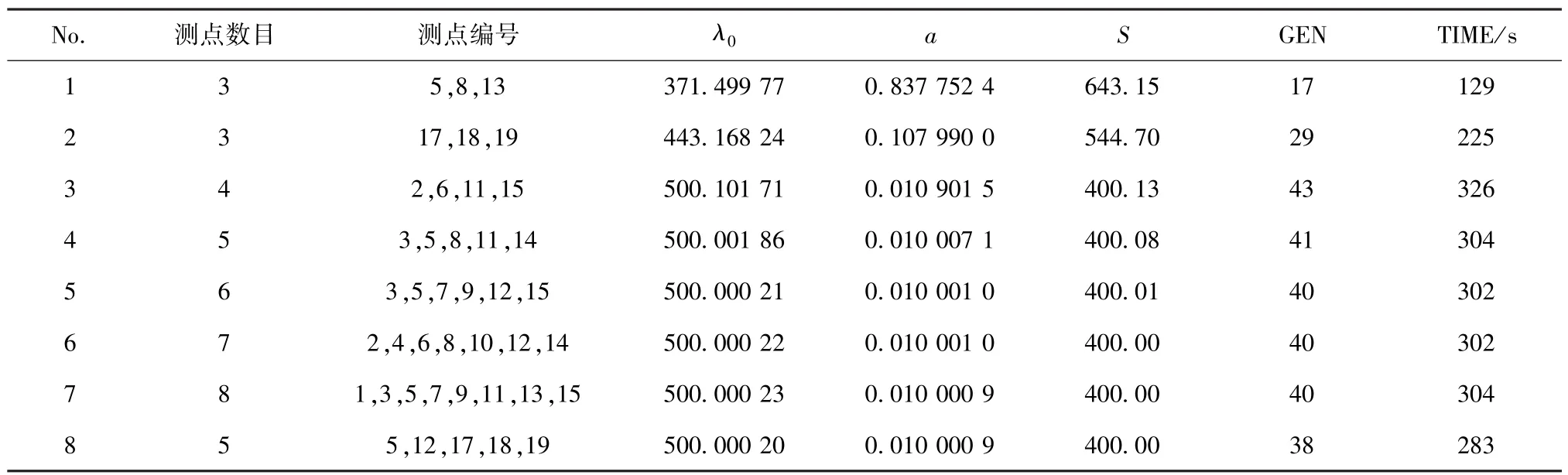
表4 测点数量及分布对最终结果的影响Table 4 Influence ofmeasuring point number and distribution on final results

5 结论

提出三种不同改进阶段的遗传算法，分别对材料导热系数与热源强度反演求解.对三种改进方法实例求解的收敛速度、计算精度的分析、比较，得到以下结论：GA⁃1克服了概率性收敛的问题；GA⁃2建立在GA⁃1基础之上，通过引入价值函数，使得GA⁃2对导热逆问题求解的收敛速度、计算精度和抗噪性能较GA⁃1得到明显提升；在GA⁃2基础上改进得到的GA⁃3，数值计算结果表明其有着更高地针对导热逆问题求解的收敛速度和计算精度，同时抗噪性也优于GA⁃2.

［1］ Lee H S.A new spatial regularization scheme for the identification of the geometric shape of an inclusion in a finite body［J］. International Journal for Numerical Methods in Engineering，1999，46（6）：973－992.

［2］ 王登刚，刘迎曦，李守巨.非线性二维导热反问题的混沌－正则化混合方法 ［J］.应用数学与力学，2002，23（8）：864－869.

［3］ Huang C H，Ozisik M N，Sawaf B.Conjugate gradient method for determining unknown contact conductance during metal casting［J］.International Journal of Heat and Mass Transfer，1991，34（7）：1779－1785.

［4］ Alifanov OM，Mikhailov V V.Solution of the nonlinear inverse conductivity problem by the iterationmethod［J］.Journal of Engineering Physics，1978，35（6）：1501－1506.

［5］ 俞昌铭.计算热物性参数的导热反问题［J］.工程热物理学报，1982，3（4）：372－378.

［6］ 吴洪潭.二维对流换热反问题的共轭梯度法求解［J］.宇航计策技术，2005，25（4）：25－27.

［7］ 薛齐文，杨海天.共轭梯度法求解非线性多宗量稳态传热反问题［J］.计算力学学报，2005，22（1）：51－54.

［8］ Tervola P.A method to determine the thermal conductivity from measured temperature profiles［J］.International Journal of Heat and Mass Transfer，1989，32（8）：1425－1430.

［9］ 朱丽娜，王广军，陈红.采用共轭梯度法求解多变量稳态传热反问题 ［J］.中国电机工程学报，2011，31（8）：58－61.

［10］ 李守巨，刘迎曦.改进遗传算法在非线性热传导参数识别中的应用［J］.工程力学，2005，22（3）：72－75.

［11］ Liu F B.A modified genetic algorithm for solving the inverse heat transfer problem of estimating plan heat source［J］. International Journal of Heat and Mass Transfer，2008，51（15－16）：3745－3752.

［12］ 王登刚，刘迎曦，李守巨，等.非线性二维稳态导热反问题的一种数值解法［J］.西安交通大学学报，2000，34（11）：49－52.

［13］ 王秀春，智会强，毛一之，等.用遗传算法求解多维导热反问题［J］.核动力工程，2005，26（1）：23－27.

［14］ 乐恺，赵琰，张欣欣.改进的遗传算法在生物组织热物性参数无损测量中的应用［J］.北京科技大学学报，2008，30（11）：1317－1321.

［15］ 杨伟超，王剑魁，张国山，王赟.基于改进遗传算法的板坯温度计算［J］.系统仿真技术，2012，8（4）：259－265.

［16］ 黄长清，刘彬，赵旻，阳康.基于改进遗传算法的铝板带热精轧轧制规程优化 ［J］.金属材料与冶金工程，2014，42 （2）：20－24.

［17］ Raudensky M，Woodbury K A，Kral J，Brezina T.Genetic algorithm in solution of inverse heat conduction problems［J］. Numerical Heat Transfer Fundamentals，1995，28（3）：293－306.

［18］ Liu F B.A hybrid method for the inverse heat transfer of estimating fluid thermal conductivity and heat capacity［J］. International Journal of Thermal Sciences，2011，50（5）：718－724.

［19］ Kohn R，Vogelins M.Determining conductivity by boundary measurements［J］.Communications on Pure and Applied Mathematics，1984，137（3）：289－298.

［20］ 黄少君，卢玫，张涛，等.适用于寻源导热反问题的改进蚁群系统［J］.工程热物理学报，2013，34（4）：694－697.

M odified Genetic Algorithm for Identifying M aterial
Thermal Properties and Strength of Heat Source

YAN F?an，LU Mei （School of Energy and Power Engineering，University of Shanghai for Science and Technology，Shanghai 200093，China）

A mathematicalmodel for two⁃dimensional nonlinear inverse heat conduction problem（IHCP）is established.Three kinds of genetic algorithm at differentmodified phase are proposed for identifyingmaterial thermal conductivity and strength of heat source. Convergence speed and calculation precision of genetic algorithms at differentmodified phase are compared.Calculation results show that the genetic algorithm modified strategy proposed achieve higher convergence speed and calculation precision.

genetic algorithm；IHCP；thermal conductivity；strength of heat source

TL329

A

2014－09－25；

2014－12－18

国家自然科学基金（51176126）资助项目

颜帆（1989－），男，硕士，从事导热逆问题优化方法研究，E⁃mail：yanfanaust＠163.com

∗通讯作者：卢玫（1957－），女，教授，从事导热逆问题研究，E⁃mail：rose_luu＠usst.com

Received date： 2014－09－25；Revised date： 2014－12－18