复杂地形下带自由表面水流的分离涡模拟

张景新

（1.上海交通大学水动力学教育部重点实验室，上海 200240；2.上海河口海岸科学研究中心河口海岸交通行业重点实验室，上海 201201）

文章编号：1001⁃246X（2015）05⁃0561⁃11

复杂地形下带自由表面水流的分离涡模拟

张景新1，2

（1.上海交通大学水动力学教育部重点实验室，上海 200240；
2.上海河口海岸科学研究中心河口海岸交通行业重点实验室，上海 201201）

将分离涡模型（DES），即一种RANS和LES的混合模型，应用于带自由表面的地表水流运动，建立一套数值仿真模型.模型基于有限体积法，水平面内采用非结构计算网格，垂向为结构化网格，对流项离散格式采用二阶TVD格式，并行基于OpenMP语言库.算例表明DES模型有助于揭示复杂地形条件下带自由表面水流的大涡拟序结构.

分离涡；拟序结构；自由表面流动；动压模型

0 引言

天然地表水流涉及洋流、河流、湖流等，对其水动力特征的研究有助于水利工程、水环境工程等的顺利开展.基于雷诺平均（RANS）的数学模型得到了广泛的应用，该类模型可描绘水流的时均流动特征，且计算效率较高.高精度数值模拟技术（LES、DNS）有助于流动细观结构的揭示，可描绘出水流运动的大涡拟序结构.但鉴于地表水流的时空尺度及复杂的边界几何形状，无论LES还是DNS近期都较难付诸于实际工程的数值模拟研究.结合LES与RANS两者的混合模型，近年来逐渐被用于工业流动的数值模拟，将其应用于地表水流运动的数值模拟，有助于进一步研究该类水流运动的若干机理问题.分离涡（DES）模型是一种RANS/LES的混合模型，由Spalart等［1］提出，后续有了长足进展［2－5］.本文将分离涡（DES）模型拓展至水动力学数值模拟，针对复杂地形条件下的带自由表面水流运动开展研究.

大尺度带自由表面的地表水流运动，依据流动的水平尺度远大于垂向运动尺度，通常采用静压假定来计算压力.但对于地形陡变、自由表面坡陡较大、局部射流等情况，需要补充动压.Casulli［6－7］建立了完全的动压模型，将压力分为静压和动压.静压的求解与常用浅水方程求解方法相似，在静压求解的基础上再通过求解压力泊松方程计算动压，可将其视为一种压力的预估—校正法.Jankowski［8］详细地论述了预估—校正法，即首先求解静压作用下的流场，称为预估步；在此基础上，通过求解动压满足的泊松（Poisson）方程，进一步更新动压作用下的流场.Li［9］将预估校正法用于表面重力波的模拟.Kocyigit等［10］和Chen等［11］在笛卡尔坐标系下求解了三维非静压模型.Fringer等［12］建立了大洋潮汐流的非静压模型.非静压模型正逐渐地被应用到大尺度地表水流运动的数值模拟中.大尺度地表水流运动模拟中，网格尺度通常较大，而粗网格不能描述局部地形的陡变，某种意义上而言，地形被数值平均了.而DES要求较高分辨率的计算网格，此时，陡变地形得以刻画.静压假定模型的模拟精度降低，动压的引入是必要的.

文章第1部分介绍自由表面水流的DES模型及数值求解方法；第2部分为模型算例，验证模型精度，讨论DES的相关技术问题.

1 数学模型

1.1 控制方程描述

基本控制方程为考虑地球自转效应（柯氏力）的三维自由表面水流运动方程，其中压力分解为静压ph＝ρg（ζ－z）和动压pn，连续性方程和动量方程如下其中g为重力加速度，柯氏力f＝2ωsinϕ，ϕ为地球纬度，ω为地球旋转角速度，ζ为水位值．若忽略动压作用，则上述控制方程退化为常用的静压方程，只包含连续性方程和水平动量方程．流场变量 qx＝Du，qy＝Dv，qz＝Dw，qσ＝Dω~，σ坐标系下的垂向速度

上述控制方程中采用了垂向σ坐标［13］变换，可拟合不规则床面及波动水面.

1.2 湍流模型

湍流模型采用S⁃A［14］一方程模型，计算变量υ~通过如下输运方程获得：

涡粘性系数υt通过υt＝的关系式计算得到．其中fv1＝χ3/（χ3＋），χ≡/υ．υ为分子运动学粘性系数．为涡量值，而＝＋（υ~/k2 d2）fv2，其中fv2＝1－χ/（1＋χfv1）．方程（6）中的耗散项系数fw由fw＝g［（1 ＋）/（g6＋）］1/6计算得到，其中各参数计算公式为g＝r＋cw2（r6－r），r≡/（）．S⁃A模型中的各计算参数分别为cb1＝0.135 5，＝2/3，cb2＝0.622，κ＝0.41，cw1＝cb1/κ2＋（1＋cb2），cw2＝0.3，cw3＝2.0，cv1＝7.1．

S⁃A模型控制方程中耗散项中的特征长度d为距固壁的距离，表征了受固壁限制湍流运动的特征长度. DES模型通过修改该变量实现RANS至LES的转换，以替代方程中的d，即d~＝min（d，CDESΔ）．表达式中Δ＝max（4A/π，Δz），A为水平网格面积，系数CDES取0.65［15］.

求解变量υ~的边界条件涉及固壁、自由表面.采用S⁃A模型，固壁边界条件满足ν~t＝0．自由表面的值可设定为常数，某些参考值可见相应的研究成果，如设定为3ν～5ν［14，16］，3ν［17－18］，也有研究取值范围为［0，0.1ν］［2］．以上的研究成果多针对气动力学.Yue等［19］针对气水两相流，采用LES模拟了明渠流动，气水交界面基于VOF法，结果表明自由表面处的涡粘性系数为几倍的分子粘性系数.

1.3 DES的“灰区”

DES模型由RANS至LES的转换过程中，存在一个“灰区”.其实质是模拟的雷诺应力不足 （Model⁃Stress Depletion，MSD），根本原因是RANS模型不能激发充分的湍流脉动量.Spalart等［3－4］为克服DES的这一缺陷，先后提出了DDES（Delayed DES）和IDDES（Improved Delayed DES）.另一种解决办法是在RANS/LES界面处通过数值方法产生湍流脉动量［20］，也可明显改善MSD问题.区域分离涡（Zonal⁃DES，ZDES）模型采用了另一种思路.与DES模型比较，DES模型由RANS至LES的转换是逐渐过渡的，即方程中的湍流特征尺度的变化是连续的.ZDES模型中的特征尺度当计算域由RANS转换至LES计算域时，直接以LES模型网格尺度代替，即Δ＝（AΔz）1/3（A为本模型中水平网格面积）．与此同时，相关的计算参数fv1，fv2和fw修改为

ZDES模型中，流动由RANS转换至LES时，特征尺度的变化及上述各参数的设定，使得模型迅速转化为LES，可激发出流动的脉动量，从而获得更多的湍流脉动.Breuer等［21］以ZDES模拟了绕平板的强分离流动，获得了与LES模拟吻合较好的结果.Deck［22－24］通过对粘性系数等的模拟结果比较，验证了ZDES在克服MSD问题方面的可行性.同时，该模型实现简便，并未增加额外的计算量.

1.4 数值方法

1.4.1 坐标变换

对于正交网格，控制体各面上的法向导数可由该面两侧单元形心处的物理量沿两点连线直接求导［7，12］.对于非正交网格系统，控制面上的导数计算可借助局部坐标系求解.本文模型，在控制面上引入局部坐标系（ξ，η），笛卡儿坐标系下的导数计算通过链导法则，转化为局部坐标系下的相应计算：

其中J＝xξyη－xηyξ为坐标系转换系数的雅可比行列式．局部坐标ξ由单元形心指向邻单元形心，η沿两单元界面，方向为ξ方向逆时针旋转，该坐标系见图1.

图1 局部坐标系Fig.1 Local coordinates on a control cell surface

1.4.2 静压模型求解

数值模型的时间积分采用半隐格式，通过参数θ实现［25］．参数θ的取值范围已有相关报道［10－11，25］．本文模型计算中θ取值0.5.

连续性方程的数值离散为

动量方程分别离散为

上述离散方程中F为显式方式离散项，包括对流项、水平粘性扩散项及柯氏力等.

首先，离散方程中仅保留静压项ph，引入临时变量，，，，η∗，单独静压作用下连续性方程的离散形式为

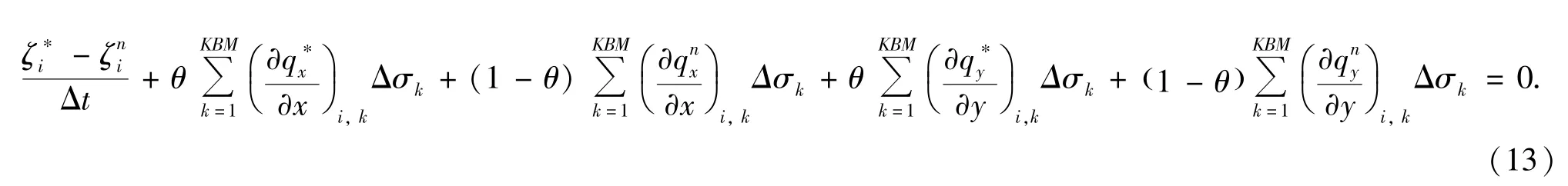
动量方程离散形式为

采用矩阵表达式，将上述离散方程改写为紧凑的表达形式，

上述表达式中的矩阵分别如下

其中，Ai是三对角形式的系数矩阵.

将方程（18）、（19）代入方程（17），可得到关于待求水位变量ζ∗的控制方程

将水位的控制方程（21）在计算单元水平面内积分，利用高斯积分定理，得到离散方程

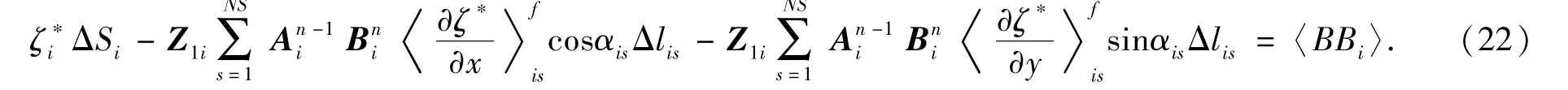
方程（22）中，符号f代表水平单元的边，ΔSi代表水平单元面积，Δlis为第s条边的边长，NS为各水平单元的总边数，（cosαis，sinαis）为第s条边的法向单位向量．单元各边建立局部坐标系（图1），表达式（22）中变量在笛卡尔坐标系（x，y）下的导数计算可借助局部坐标系（ξ，η）下的相应计算获得，具体表达式

将表达式（23）写成如下的紧凑形式其中各系数为

代数方程组（24）采用双共轭梯度法（Bi⁃CGSTAB）求解，可获得新时刻的水位变量ζ∗；新时刻的流速变量，通过方程（18）和（19）进一步求解得到.如果模型仅做静压计算，上述的求解变量即为n＋1时步的最终变量，一个计算循环完成；若模型设定为非静压模式，需要进一步求解动压项.

1.4.3 动压模型求解

动压模型在静压求解的基础上进行，动压pnn＋1作用下的控制方程

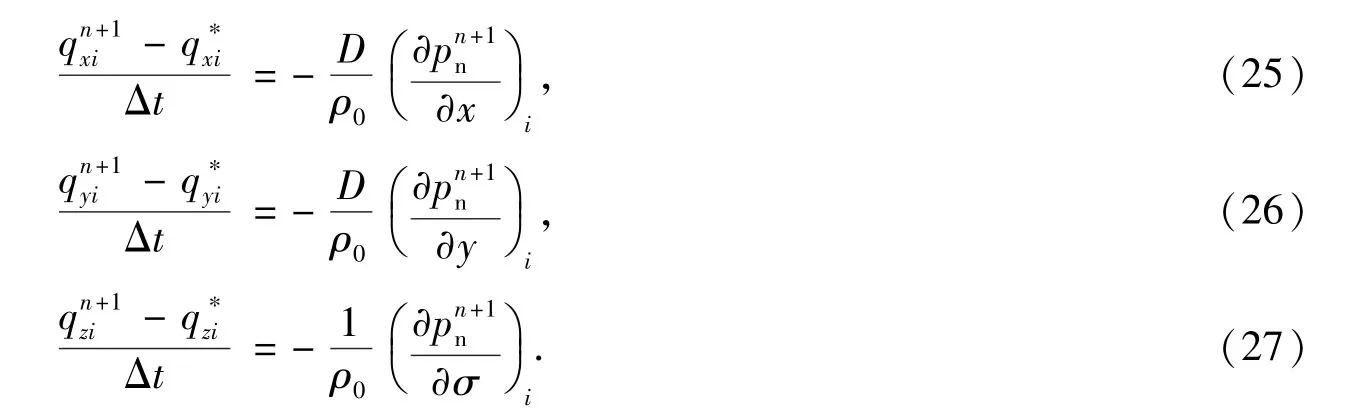
n＋1时刻更新的流场须满足连续性条件，即流速变量满足连续性方程（1）.方程（1）中不显含变量qz，首先需要将方程（1）改写为将方程（25）、（26）和（27）代入方程（28），得到如下关于动压pn＋1n的泊松方程上述控制方程中关于动压pn＋1

将方程（25）、（26）和（27）代入方程（28），得到如下关于动压pn＋1n的泊松方程

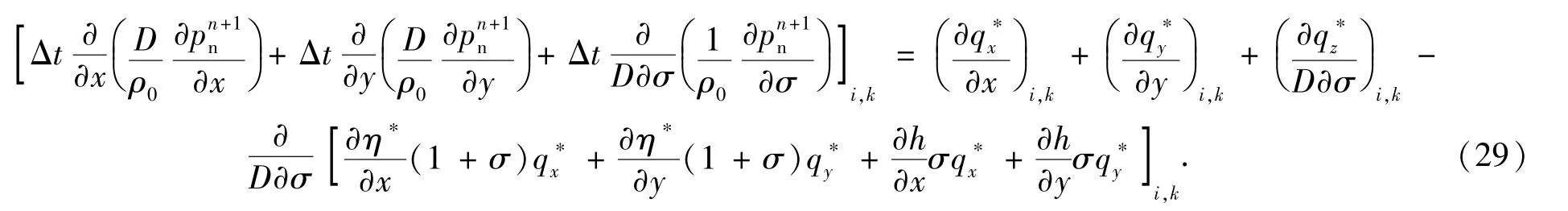
其中各系数的计算表达式

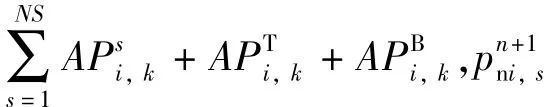
1.4.4 TVD离散格式

本模型采用二阶TVD数值格式离散动量方程的对流项.有限体积法中，界面处的任一物理量〈φ〉f通过如下插值法获得

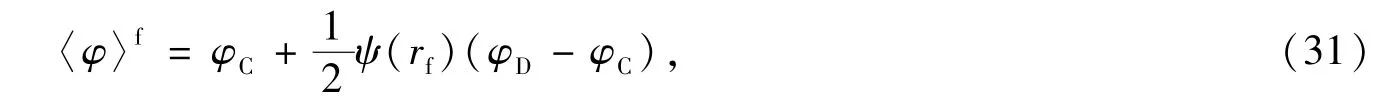
其中符号f代表界面，φD和φC分别为该界面顺风向和迎风向单元形心处的相应变量．通过通量限制器ψ（rf），实现二阶的TVD格式．ψ（rf）是变量rf的相关函数，相关的计算可参考文献Darwish等［26］.本模型引入了如下的通量限制器：

SUPERBEE ψ（rf）＝max（0，min（1，2rf），min（2，rf））；

MINMOD ψ（rf）＝max（0，min（1，rf））；

OSHER ψ（rf）＝max（0，min（2，rf））；

MUSCL ψ（rf）＝（rf＋ rf）/（1＋ rf）；

VAN LEER ψ（rf）＝（rf＋ rf）/（1＋rf）；

SWEBY ψ（rf）＝max（0，min（1，1．5rf），min（1.5，rf））；

QUICK ψ（rf）＝max（0．0，min（2rf，（3.0＋rf）/4．0，2．0））；

UMIST ψ（rf）＝max（0．0，min（2rf，（1．0＋3rf）/4．0，（3．0＋rf）/4．0，2．0）；

MC ψ（rf）＝max（0．0，min（（1．0＋rf）/2．0，2．0，2．0rf））．

模型中的上述TVD格式均做了严格验证，下文计算采用OSHER格式.

1.4.5 湍流S⁃A模型的离散

控制方程（6）采用有限体积法（FVM）离散求解，具体离散格式如下

其中F为显式方式离散项，包括对流项、水平粘性扩散项等；生成项与耗散项采用隐格式求解.上述离散方程的具体求解过程及所形成的三对角方程组的求解同动量方程的相应求解方法.

2 模型应用

将上述数值模型应用于自由表面水流运动的模拟，重点考察小尺度涡结构，获得流动的细观特征.本文针对系列沙丘地形下的水流运动开展小尺度涡结构的模拟研究，模型计算细节及结果分析如下文所述.

沙丘地形下带自由表面水流运动

单一沙丘的几何形状与Balachandar等［27］的实验相同.该实验共布设了22个相同的沙丘，详细测量了第17个沙丘范围内的流场.图2描绘了单个沙丘的几何形状及测量点位置.本文模拟了5个沙丘组成的系列地形条件下的水流运动，重点考察局部流动的涡结构，讨论了流动的沿程演化等问题.覆盖沙丘地形的计算域网格尺度设计满足LES的要求，向上下游开边界网格尺度逐渐增加，直至完全处于RANS计算范畴.依据网格尺度设计的计算域分区见图3，其中RANS计算域不仅覆盖近底床区域，还延伸至上下游开边界处的全水深区域.对于LES，开边界的入流条件，即来流的湍流脉动信息的充足与否对计算影响明显.而本算例中开边界设置为RANS计算域，没有提供流场脉动量信息，势必对湍流小尺度涡结构的模拟产生影响.本算例设计了5个连续的沙丘地形，预期前部沙丘地形诱导湍流脉动，为后续流场提供湍流脉动成分.与LES模拟中采用数值生成脉动量的方法相比较，可视其为湍流脉动产生的物理方法.若仅研究沙丘地形下的流动特征，布置5个相同的沙丘地形，显然效率不高.天然水流（如河流），空间尺度不允许全计算域采用LES，而只能局部关注区域采用LES，其它区域采用RANS.天然河流等无论地形，还是岸线均是不规则的，这些不规则的几何形状影响流动，可激发出湍流的脉动量.正如本算例所设置的地形，可作为脉动量生成的物理因素.上游来流中脉动量的重要性，通过以下模拟结果进行分析.

图2 沙丘地形及测点位置Fig.2 Geometry of dunes

图3 计算域及RANS/LES区域划分Fig.3 Schematic of computational zones

本算例以上游水深L和自由表面来流速度U0为特征量，控制参数为Re＝5．7×104，且Fr＝0.44．水平网格最高分辨率5mm，垂向网格设计满足近壁面第一层网格中心点z＋≈1，继而垂直向上以1.15的伸展率逐渐增加，直至达到5mm.明渠流动的大涡尺度受水深这一特征尺度限制，相关研究［28］给出了满足LES计算需要的网格尺度与水深的关系，可作为明渠水流LES模拟网格设计的参考.本文网格尺度与水深关系为L/24（L为上游水深值）.DES计算中RANS和LES的区域划分以网格尺度控制，本算例中5mm的计算网格控制了RANS/LES的分区界面位于O（10z＋），而该区域是近壁湍流发展的活跃区域［20］.

模型首先以静压模式运行至流动稳定状态，再切换至动压模式计算至稳定状态，继而由RANS模式转换至DES模式.在DES模型运行过程中，记录若干点流动变量的计算值，当达到统计意义上的稳定状态后，再继续运行15个大涡周期（L/uτ），uτ为上游流场的平均摩阻流速.该15个大涡周期时段的流场模拟信息用于流动分析，数据采样频率100Hz.

时均流动分析

对于本文系列沙丘地形下的流动，RANS模型获得稳定的定常流动，然而DES模型预报了小尺度涡的脉动，流动是非定常的，仅存在统计意义上的稳定状态.将流场的时间序列模拟结果作时均分析，可获得时均流场信息.

实验测量了图2所示6条垂线位置处的流速时间序列，并给出了相应的流场特征.6个测点相对于沙丘峰值点的位置分别为x/h＝2，4，5，6，12和18.本文算例分别记录了第一、第三和第五个沙丘相应的6个测点的流场信息，用于模型验证.图4给出了流向速度的对比，其中符号为实测值，线分别对应于三个沙丘的计算值.分析6个测量点的模拟结果与实验结果，第五个沙丘范围内的相应计算值与实测值吻合最好，精度最高.第一个沙丘范围内的相应计算值精度最低.而RANS模型的结果显示几个沙丘范围内的计算值基本一致，并未显示出沿流向流场的明显变化.分析本文DES模型的网格设计，入口为RANS计算域，对于其后的LES计算域而言，输入的湍流脉动成分不足，导致湍流场发展不充分.当水流流经沙丘时，该局部地形变化将诱发流场脉动，该脉动量可视为其后流场的输入条件，故模拟结果显示湍流场沿程逐渐发展，至第五个局部沙丘范围时，模拟结果与实测值吻合精度已明显提高.

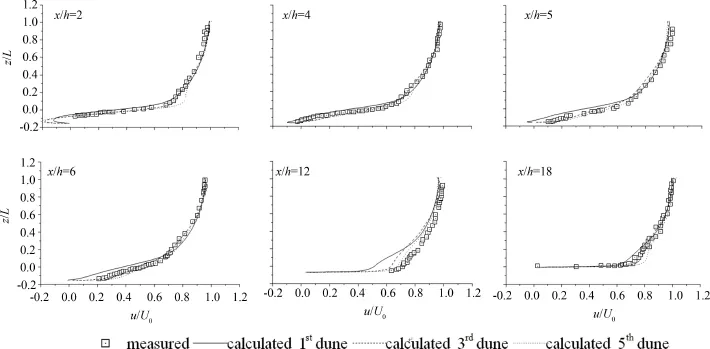
图4 流向速度验证Fig.4 Stream velocity at different sites

计算时均Reynolds应力〈－u′w′〉，并与实测值比较，图5给出了6个测量点处两者的比较.图中符号为实验测量值，线分别为第一、第三和第五个沙丘范围内相应位置的计算值.Reynolds应力〈－u′w′〉的极值大致出现在z/L＝0，数值模拟结果与实测值吻合较准确.第一个沙丘范围内的计算值明显低于实测值，第三和第五个沙丘范围内的相应计算值与实测值符合的较好.该结果再次验证了入流湍流脉动量对计算结果有明显的影响.系列沙丘地形条件下，水流流经某个局部沙丘，将激发湍流脉动量.对后续流场，该脉动量可视为入流条件，故模拟精度沿流向逐渐提高.图5显示第三个沙丘地形模拟结果较之第五个沙丘范围内的相应计算结果精度更高，与湍流场逐渐充分发展的预期存在偏差，这可能在于流动经过这一系列沙丘后，尚未达到统计意义上的稳定状态.相应的实验测量均取在第17个沙丘范围内完成，也是考虑到湍流场的充分发展需要一定的沿程距离.

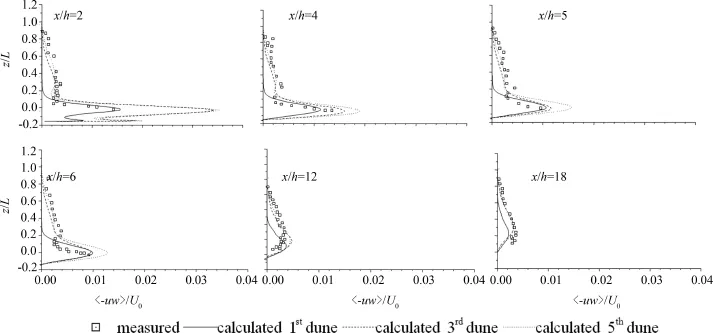
图5 Reynolds应力模拟与比较Fig.5 Predicted mean Reynolds stress and experimental data

瞬时流动分析

图6 Q的瞬时等值云图（灰度由涡量渲染）Fig.6 Snapshot of criterion Q isosurfaces contoured by vorticity

较之RANS模型，DES可模拟小尺度的涡结构，给出流动的细观特征.湍流场的复杂涡结构可以用速度梯度张量的第二不变量描述，即变量Q ＝（ΩijΩij－SijSij）/2＞0，其中Sij和Ωij分别是速度梯度张量ΔV的对称和反对称部分．图6给出了Q＝5的瞬时云图，并以涡量值渲染.小尺度涡沿流向逐渐发展，模拟结果逐渐显示出大涡模拟的内容.上游局部沙丘激发出湍流脉动，从而促使湍流场充分发展.这一算例的设计，入流边界条件并未包含湍流脉动信息，但流动的发展，特别是地形变化引起的水流分离运动，极大地激发出了脉动量，使得小尺度涡结构向下游越发清晰，湍流运动逐渐充分演化.

考察湍流场的沿程演化，分别在第一、第三和第五个沙丘范围内取一横断面，各断面相对沙丘峰值点位置为0.2λ（λ为单个沙丘全长）.图7描述了各个断面内的瞬时流速矢量分布及涡量分布.瞬时流速矢量及涡量分布显示了不同断面模拟结果中小尺度涡的发展情况，即湍流场充分发展的程度.数值模拟结果所包含的涡结构是否充分，是大涡模拟成功与否的一个标志.结果显示来流所含湍流场脉动信息对湍流运动模拟、大涡结构的捕获非常重要.

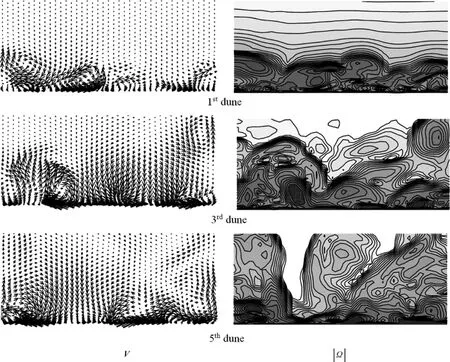
图7 不同断面内的瞬时流场（x/λ＝0.2）Fig.7 Instantaneous flows at different cross⁃sections（x/λ＝0.2，withλthe dune length）

通过时均处理，可获得时均流场信息，进一步提取瞬时流场脉动量，同样可分析湍流场的沿程发展.图8给出了中垂面（y＝0，x⁃z）内瞬时脉动速度（u′，w′）的分布，分别对应于第一、第三和第五个沙丘范围.与前述分析类似，沿流向，脉动速度逐渐增大，湍流运动逐渐发展.大涡模拟中通常采用数值方法在来流中生成脉动速度，本算例的入流开边界处于RANS计算域，缺少脉动量的输入.而局部地形变化激发的湍流脉动量，可视为其后流场模拟的入流条件，故极大地提高了模拟精度.若针对天然河流采用该计算方法，仅在重点关注区域采用LES，开边界局部仍采用RANS，将简化边界条件的设定.同时，天然河道的不规则几何特征将极大地激发湍流脉动，从而为LES模拟区域提供充分的脉动信息.

图8 中垂面（y＝0，x⁃z）内瞬时脉动速度场（u′，w′）的沿程演化Fig.8 Instantaneous velocity vectors（u′，w′）in the central x⁃z plane

3 结论

将静压假定条件下的自由表面浅水动力学模型拓展至考虑动压的数学模型，极大地拓宽了模型的应用范围.通过修改一方程湍流模型（S⁃A模型），建立了自由表面水流运动的DES数值模型.建立的数值模型基于FVM，采用非结构网格，并基于OpenMP技术实现了软件的并行化.DES模型较之RANS模型，在小尺度涡结构的捕获方面具有一定的优势，可用于流动细观特征的研究.通过RANS与DES模型算例的对比，可知DES模型能够提供更丰富的小尺度旋涡信息，而这些在RANS模型中均被时均化处理方法所掩盖.从流动细观入手，通过适当的统计方法，进而获得流动的宏观特征，较之直接的时均化方法研究，可获得更加丰富的流场信息.

DES模型局部采用RANS，强分离区采用LES，对于高雷诺数、复杂边界几何条件的流动模拟是兼顾了计算效率和计算精度的一种可行办法.但也存在一些问题，最突出的一个就是“灰区”问题，即计算模型由RANS转换至LES时，所输入的湍流脉动量不足.对于开边界处于RANS区的情况，入流脉动量不足也将导致计算结果精度降低.

天然大尺度的自由表面水流运动，多为高雷诺数、复杂几何边界条件，LES的实现尚有一定的难度.而采用LES/RANS混合模型，既可实现局部关注区域的高分辨率模拟，又可大大降低计算量，是一种可推广应用的数值方法.

［1］ Spalart PR，Jou W H，Strelets M，Allmaras SR.Comments on the feasibility of LES forwings，and on a hybrid RANS/LES approach［M］∥Liu C，Liu Z.Advances in DNS/LES.Greyden Press，1997.

［2］ Spalart PR，Allmaras SR.A one⁃equation turbulencemodel for aerodynamic flows［J］.La Recherche Aérospatiale，1994，1：5－21.

［3］ Spalart PR，Deck S，Shur M L，Squires K D，Strelets M K，Travin A.A new version of detached⁃eddy simulation，resistant to ambiguous grid densities［J］.Theor Comput Fluid Dyn，2006，20：181－195.

［4］ Shur K L，Spalart PR，Strelets M K，Travin A K.A hybrid RANS⁃LES approach with delayed⁃DES and wall⁃modelled LES capabilities［J］.International Journal of Heat and Fluid Flow，2008，29：1638－1649.

［5］ Spalart PR.Detached⁃eddy simulation［J］.Annu Rev Fluid Mech，2009，41：181－202.

［6］ Casulli V.A semi⁃implicit finite difference method for non⁃hydrostatic，free⁃surface flows［J］.International Journal for Numerical Methods in Fluids，1999，30：425－440.

［7］ Casulli V，Zanolli P.Semi⁃implicit numericalmodeling of nonhydrostatic free⁃surface flows for environmental problems［J］. Mathematical and Computer Modeling，2002，36：1131－1149.

［8］ Jankowski JA.A non⁃hydrostatic model for free surface flows［D］.Germany：University of Hannover，1999.

［9］ Li B，Fleming C A.Three⁃dimensionalmodel of Navier⁃Stokes equations for water waves［J］.Journal of Waterway，Port，Coastal and Ocean Engineering，2001，127（1）：16－25.

［10］ Kocyigit M B，Falconer R A，Lin B.Three⁃dimensional numericalmodeling of free surface flowswith non⁃hydrostatic pressure ［J］.International Journal for Numerical Methods in Fluids，2002，40：1145－1162.

［11］ Chen X J.A fully hydrodynamic model for three⁃dimensional，free⁃surface flows［J］.International Journal for Numerical Methods in Fluids，2003，42：929－952.

［12］ Fringer O B，Gerritsen M，Street R L.An unstructured⁃grid，finite⁃volume，nonhydrostatic，parallel coastal ocean simulator ［J］.Ocean Modeling，2006，14：139－173.

［13］ Phillips N A.A coordinate system having some special advantages for numerical forecasting［J］.Journal of Meteorology，1957，14：184－185.

［14］ Spalart PR.Strategies for turbulencemodelling and simulations［J］.International Journal of Heat Fluid Flow，2000，21：252 －263.

［15］ Shur M，Spalart P R，Strelets M，Travin A.Detached⁃eddy simulation of an airfoil at high angle of attack［C］∥Fourth International Symposium on Engineering Turbulence Modelling and Experiments，Rodi W，Laurence D，eds.Corsica：Elsevier，New York，24－26 May，1999.

［16］ Spalart PR，Rumsey C L.Effective inflow conditions for turbulencemodels in aerodynamic calculations［J］.AIAA Journal，2007，45（10）：2544－2553.

［17］ Aupoix B，Spalart PR.Extensions of the Spalart⁃Allmaras turbulencemodel to account for wall roughness［J］.International Journal of Heat and Fluid Flow，2003，24：454－462.

［18］ Eca L，Hoekstra M，Hay A，Pelletier D.A manufactured solution for a two⁃dimensional steady wall⁃bounded incompressible turbulent flow［J］.International Journal of Computational Fluid Dynamics，2007，21（3/4）：175－188.

［19］ YueW，Lin C L，Patel V C.Large eddy simulation of turbulent open⁃channel flow with free surface simulated by level set method［J］.Physics of Fluids，2005，17：1－12.

［20］ Keating A，Piomelli U.A dynamic stochastic forcingmethod as a wall⁃layermodel for large⁃eddy simulation［J］.Journal of Turbulence，2006，7（2）：1－24.

［21］ Breuer M，Jovicˇic＇N，Mazaev K.Comparison of DES，RANS and LES for the separated flow around a flat plate at high incidence［J］.International Journal for Numerical Method in Fluids，2003，41：357－388.

［22］ Deck S.Numerical simulation of transonic buffet over a supercritical airfoil［J］.AIAA J，2005，43（7）：1556－1566.

［23］ Deck S.Zonal⁃detached eddy simulation of the flow around a high⁃lift configuration［J］.AIAA J，2005，43（11）：2372－2384.

［24］ Deck S，Weiss P，Pamiès M，Garnier E.Zonal detached eddy simulation of a spatially developing plate turbulent boundary layer［J］.Computers＆Fluids，2011，48：1－15.

［25］ Casulli V，Cattani E.Stability，accuracy and efficiency of a semi⁃implicitmethod for three⁃dimensional shallow water flow ［J］.Computers and Mathematics with Applications，1994，27（4）：99－112.

［26］ Darwish MS，Moukalled F.TVD schemes for unstructured grids［J］.International Journal of Heat and Mass Transfer，2003，46：599－611.

［27］ Balachandar R，Polatel C，Hyun B⁃S，Yu K，Lin C⁃L，YueW，Patel V C.LDV，PIV，and LES investigation of flow over a fixed dune［C］∥Proc，Symp Held in Monte Verta：Sedientation and Sediment Transport，Monte Verita，Switzerland，Kluwer Academic，Dordrecht，2002：171－178.

［28］ Hinterberger C，Frohlich J，RodiW.Three⁃dimensional and depth⁃averaged large⁃eddy simulations of some shallow water flows ［J］.Journal of Hydraulic Engineering，2007，133（8）：857－872.

A Detached Eddy Simulation Model for Free Surface Flows w ith Uneven Bottom

ZHANG Jingxin1，2
（1.MOE Key Laboratory ofHydrodynamics，Shanghai Jiao Tong University，Shanghai 200240，China；
2.Key Laboratory of Estuarine＆Coastal Engineering，Ministry of Transport，Shanghai 201201，China）

A detached⁃eddy simulation（DES）model is proposed based on a fully hydrodynamic pressuremodel instead of hydrostatic model.The numerical scheme is based on finite volumemethod（FVM）on unstructured grids in the horizontal plane，andσcoordinate in vertical direction to fix free surface and uneven bottom.The in⁃house codes are paralleled using OpenMP.The proposed model is shown particularly effective in prediction of small⁃scale vortical structures.

detached eddy simulation；coherent structure；free surface flow；hydrodynamic model

O352

A

2014－12－11；

2015－01－13

国家重点基础研究发展计划（973）（2014CB046200）及水利部公益性行业科研专项经费（201401027）资助项目

张景新（1975－），男，副教授，从事环境流体力学研究，E⁃mail：zhangjingxin＠sjtu.edu.cn

Received date： 2014－12－11；Revised date： 2015－01－13