校准条件下的数值模拟不确定度量化方法

马智博，殷建伟，李海杰，刘 全

（1.北京应用物理与计算数学研究所，北京 100088；2.长沙机电产品研究开发中心，湖南长沙 410100）

文章编号：1001⁃246X（2015）05⁃0514⁃09

校准条件下的数值模拟不确定度量化方法

马智博1，殷建伟1，李海杰2，刘 全1

（1.北京应用物理与计算数学研究所，北京 100088；2.长沙机电产品研究开发中心，湖南长沙 410100）

当存在众多不确定输入因素时，不确定度的传递分析往往导致对数值模拟不确定度的过高估计.利用校准行为能够消减系统级数值模拟中认知不确定度的客观机制，提出一个综合利用已有系统级试验对比信息和新增建模与模拟传递信息的不确定度量化方法，结合一个虚拟试验的例子对该方法进行展示和验证.

数值模拟；不确定度量化；校准；可靠性认证

0 引言

在投入应用之前，建模与模拟（Modeling＆Simulation，M＆S）技术需要经过验证（Verification）、确认（Validation）和认可（Accreditation）过程，以评估其可信度并获取工程应用所需的资质［1－2］.事实上，即便经过充分的验证和确认，也难以完全发现并彻底解决M＆S中的所有问题，再加上不可避免的离散误差，对复杂物理过程的数值模拟往往会产生相对于真值的系统性偏离，因而常常通过校准（Calibration）措施给予纠偏以提高模拟结果与试验结果的一致性.用经过校准的模拟程序对新的复杂对象进行模拟计算，是现实中普遍存在并将长期存在的工程预测方法.当不能进行新对象的系统级试验时，对校准后数值模拟的预测结果进行不确定度量化，是可靠性认证与评估所面临的一个重要科学问题［3］.

认证的对象为抽象的事物类（如型号），评估的对象为具体的事物例（如产品）［4］.型号经过认证后获得定型，定型产品经过库存和服役等过程后，可能发生状态上的改变，往往需要分期评估.为全面考察各种工程因素的影响，新型号认证一般会安排较多的系统级试验，试验数据可用于数值模拟的系统级校准、确认和不确定度量化.当不能进行新对象的系统级试验时，需要针对改变后的设计参数和新增加的工程因素进行数值模拟及其模拟结果的不确定度量化.

如果不能进行新对象的系统级试验，数值模拟不确定度量化的信息主要来自两个方面：其一是对比信息，即通过原型对象的系统级试验数据与数值模拟的对比而得到的不确定度信息，利用模型空间中不确定度从确认域到应用域的外推技术，可以将该信息转换为能够直接反映新对象系统级数值模拟的不确定度信息［4］；其二是传递信息，即借助总体计算程序和扰动分析方法，将较低层级建模与模拟不确定度信息传递到新对象系统级数值模拟的不确定度信息［5］.

可靠性分析往往受困于信息缺乏，多源信息的整合因此变得迫切.虽然对比信息和传递信息分别来自不同的认知途径，但反映的是同一个问题，将二者进行整合，既有现实需求，又有科学上的合理性和可行性.

基于单信息源的不确定度量化已有较好的方法基础.Oberkampf根据数值模拟结果以及试验结果的均值和标准差，给出了概率框架下基于对比分析的数值模拟误差量化方法［1］，Helton总结了认知不确定度传递分析的敏感度方法和蒙特卡罗抽样方法［6］，刘全用非嵌入多项式混沌方法进行了炸药状态方程模型参数不确定度对爆轰计算结果不确定度的传递分析［7］.将对比信息从确认域外推到应用域的不确定度量化方法也被提出并逐渐投入使用［4，8］，而有关这两类信息的整合，仍是目前面临的技术瓶颈.

数值模拟的不确定度主要为认知不确定度，宜用区间理论来表达并进行信息整合，不确定度量化应当遵循真值覆盖原则和最小化原则［4］.如果量化结果仅利用外推后的对比信息，则会因为没有充分考虑新对象建模和模拟所新增加的认知缺陷，容易导致不确定度估计结果偏小而违背真值覆盖原则，最终增加不合格对象被接收的风险，如果把外推后的对比信息和不确定度的整体传递信息直接相加或仅仅利用整体传递信息，均可能使不确定度估计结果被不合理地放大而违背最小化原则，从而增加合格对象被拒收的风险.

根据认知科学中对比信息和传递信息之间的容斥关系以及不确定度量化的基本原则，本文将经过外推的系统级对比信息作为不确定度的基本组成部分，将新对象建模和模拟所新增加的不确定度传递到系统级的计算结果中，作为不确定度的增量部分，然后将二者进行相加作为新对象数值模拟的不确定度，并结合一个黎曼问题及其虚拟试验对该不确定度量化方法进行展示和验证.

1 数值模拟校准及其技术特征

提高计算结果与试验结果一致性的途径有两个，其一是全面提高认知能力，降低数值模拟中每个技术环节的认知不确定度，这也是数值模拟发展的理想途径，其二是基于现有认知能力，人为地让不同技术环节所产生的认知误差相互补偿.数值模拟校准在较大程度上依赖于误差补偿机制，但这种补偿作用只在较小的模型范围内有效，随着模拟对象远离那些用以校准的试验对象，数值模拟不确定度往往增加很快.

本文提及的模型包括实体模型和物理模型，前者指具体的特殊工程对象，包括部件的材料选用、密度与质量、形状与尺寸、动作过程的初边条件等工程设计参数，后者指抽象的一般物理规律，包括描述材料力学属性的本构关系和状态方程、描述相关物理过程（如爆轰、湍流和传热等）的模型方程以及描述物质运动普遍规律的三大守恒方程等.实体建模的不确定度往往决定于静态测量的不确定度，物理建模可能涉及更多的动态测量以及基于测量结果和近似理论的逆向运算，因此，物理建模所引起的数值模拟不确定度一般较大.

结合试验进行的校准行为，主要体现在对模型形式、计算方法和选定的校准参数进行调整并把它们固定下来［2］，校准参数一般来自计算参数、物理参数或可调参数.可调参数可理解为缺乏明确数学和物理含义或缺乏确切赋值信息但对最终数值模拟结果有明显影响的参数.通过充分的验证和确认，可有效减少可调参数的数量，提高数值模拟的预测能力，但由于数值计算对应非零的时间和空间离散尺度，离散误差不可避免，再加上模型形式的近似性和计算方法在模拟复杂问题时能力的欠缺，可调参数的存在往往难以避免［9］.

校准过程一般基于某一范围内的实体模型，本文将实体模型空间中的这个范围称为校准域.校准之后所进行的确认活动，也有对应的确认域，其中模拟结果和试验结果的对比分析，被用于确认域内数值模拟的不确定度量化.

校准过程完成以后，计算程序及其相关的模型参数即被固化，但固化通常具有相对性和阶段性.相对性主要表现在描述物理规律的模型参数在取值上与特定计算方法和计算参数有关，并非完全基于对物理的认识，而阶段性表现在固化版本通常是暂时的，随着数值模拟技术的发展，模型和参数也会随之改变.

演绎和归纳是认识事物的两个基本方法，前者基于特定条件和普遍规律来推断事物的发展结果，是不确定度传递分析的基础，后者通过实践和观察来总结事物的发展结果，是不确定度对比分析的基础.对比信息直接来自系统层级的实践活动，因此可信度更高，在进行信息整合时，对比信息的权重因子一般要远大于传递信息.

我们认为，经历校准后的数值模拟具有如下特点：

1）校准域内系统级数值模拟的不确定度能够得到有效消减，但随着实体模型远离校准域，误差补偿作用逐渐减弱，新对象模拟结果对真值的背离会逐渐增大；

2）确认域内由对比分析得到的不确定度可外推至应用域，但外推结果不能充分反映新对象建模和模拟所导致的新增不确定度；

3）系统级以下物理建模和数值计算的不确定度并不因为校准而得到必然的消减，由传递分析得到的不确定度往往较大；

4）如果对比信息和传递信息均反映同一数值模拟的不确定度，进行信息整合时，权重分配应以对比信息为主；

5）当确认域外的新对象不能进行试验时，数值模拟不确定度存在两个独立的信息来源：其一是系统级确认域内来自对比的不确定度信息，其二是系统级以下新增的建模和模拟不确定度所传递到系统级的不确定度信息，二者具有可加性，可基于区间理论进行信息整合.

2 校准条件下的不确定度量化

需要解决的关键问题之一，是如何整合对比信息和传递信息，并使量化方法符合真值覆盖原则和最小化原则［4］.

实物试验可消减认知不确定度，但不能消减偶然不确定度.对偶然不确定度，可根据各自的信息量来分配信息整合的权重，然后用概率框架下的贝叶斯理论或其它技术途径进行对比信息和传递信息的整合［10－11］.数值模拟主要产生认知不确定度，只要对比信息存在，一般可把传递信息的权重赋零，主要使用对比信息进行不确定度量化.

当没有新对象的系统级试验时，无直接的对比信息可利用，不确定度量化的可能方案有：

1）仅仅利用传递信息；

2）仅仅利用外推后的对比信息；

3）同时利用以上两种信息.

第一方案未利用原有的系统级对比信息，由传递给出的认知不确定度不能得到有效消减，传递过程产生的不确定度难以量化，低层级数值计算造成的不确定度也难以传递到系统层级.第二方案可能漏掉新对象建模和模拟所新产生的不确定度.第三方案有更加合理的思想基础，但需要设计一套恰当的实施方法，最大限度地减少上述问题造成的影响.

基于第三方案，本文建议，首先将新对象由传递得到的数

传递信息一般由三部分组成，结合式（1），有如下近似表达式

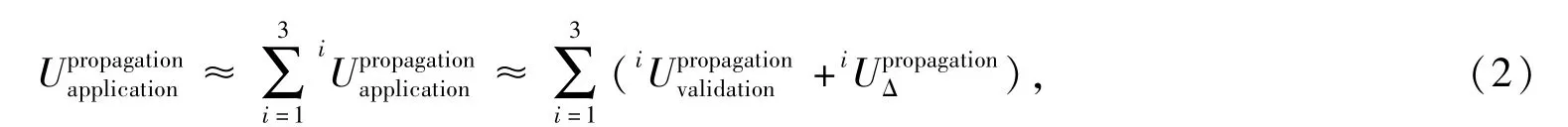
其中1Upropagation，2Upropagation，3Upropagation分别表示实体建模、物理建模和数值计算三个技术环节所传递到系统级的数值模拟不确定度.

新对象数

综上所述，可据如下步骤进行数值模拟不确定度的量化：

1）结合校准试验，进行数值模拟校准，然后完成对计算程序和相关参数的固化；

2）结合确认试验，进行系统级确认域内的对比分析和不确定度量化；

3）根据不确定度随实体模型参数的变化规律，用确认域内的不确定度信息外推新对象数值模拟的不确定度；

5）根据公式（3）得到新对象数值模拟的总体不确定度.

3 基于对比分析的不确定度量化

试验对象的加工随机性和测试随机性都会使试验结果产生偶然不确定度，但该不确定度并非由数值模拟产生，因此，基于对比分析的不确定度量化方法，要恰当地构造统计量，屏除这类不确定度的影响，同时有效地揭示真正的数值模拟不确定度信息.

在工程实践中，基于试验的对比分析有两种情形：

1）一对一，即一次数值模拟对应一次试验；

2）一对多，即一次数值模拟对应多次试验.

在一对一情形中，需要对每次试验的对象进行单独测量，然后将测量结果用于实体建模和物理建模，每个试验对象均有相应的数值模拟结果和试验结果，在扣除测试误差后，两者之间的差别能够直接地反映试验对象的数值模拟误差.如果试验和模拟次数均为n，可按下式提取数值模拟的不确定度：

一对多情形往往对应于重复性试验，仅基于设计方案的公称参数或实际加工的中值参数进行实体建模和物理建模，最终只产生一套数值模拟结果.虽然每一个试验对象都按照同样的设计方案进行加工制造，但产品加工和试验测试的随机性会导致试验结果的随机性.为了屏除随机性干扰信息，本文建议从数值模拟结果与试验均值之间的差异中挖掘数值模拟的不确定度信息，具体公式

本文取置信度β＝0.95，t（1－β）/2，ν为自由度为ν的t分布的（1－β）/2分位数，ν＝n－1．

当所有试验对象均处于某设计点附近且n足够大时，式（4）、（7）给出的结果趋于一致.

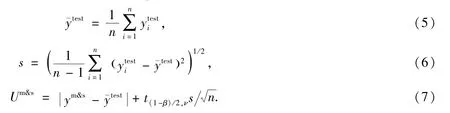
4 实例演示

4.1 问题描述

图1所示的实体模型对应一维黎曼问题，共有两个物质区域，左端区域相当于高压气体，其初始时刻的压强、密度、内能和速度分别为p1，ρ1，e1，v1，右端区域相当于重金属材料，其初始时刻的压强、密度、内能和速度分别为p2，ρ2，e2，v2．两区在零时刻的初速度均为零，从零时刻开始，在物质界面处产生一个向左传播的膨胀波和向右传播的冲击波，金属材料在高压气体的推动下向右运动，本例所关心的系统级输出量是10μs时物质界面移动的距离D.

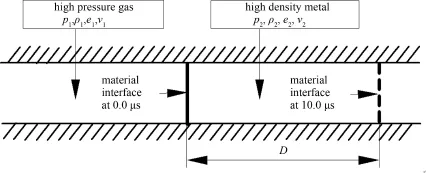
图1 实体模型示意图Fig.1 Sketchmap of entitymodel

物理模型主要涉及两种材料的状态方程，左端的气体选用理想气体状态方程p＝（γ1－1）ρe，音速方程c右端的金属也被视作流体，选用凝聚介质实用状态方程p＝（ρ－ρ0）＋（γ2－1）ρe，音速方程 ，其中γ1和γ2分别为两种材料的多方指数，c0为初始音速.

本例将上述实体模型看作一个产品型号，并假定库存老化仅导致两个物理参数发生改变，其一是气体的初始内能e1（初始压强与初始内能相关，不作为独立的模型变量），其二是金属的多方指数γ2．因二者均为库存时间t的函数，可基于库存时间建立实体模型的模型空间，并在该模型空间中定义校准域、确认域和应用域.

要解决的问题是，当不能对库存产品进行新的系统级试验时，如何基于已有的0年～50年库存期产品的系统级试验结果及其对应的数值模拟结果，量化80年库存期产品数值模拟预测的不确定度.

4.2 试验设计

模型校准、模型确认以及对不确定度量化方法的检验将涉及试验，该例存在系统级输出量的精确解D∗，因此拟用虚拟试验代替真实试验，并需要预先确定一套表达不同库存期产品真实变化规律的实体模型和物理模型——本文称之为真实模型.真实模型只用于产生虚拟试验数据，文中不予展示.

虚拟试验（下文简称试验）的作法是，首先结合真实模型确定模型参数的设计值，然后在设计值上附加一个虚拟随机量（以模仿真实的加工制造随机性），将模型参数转变为随机变量，接着对该随机变量进行抽样，把抽样结果视作试验样品真实状态的模型参数，并据此求出各试验样品所对应的系统级输出量的精确解.为了模仿真实试验的测试随机性，也通过附加虚拟随机量的方法将精确解转变为随机性系统级输出量，对该输出量进行抽样，便可获取相当于真实试验的测试结果.

表1 虚拟随机变量的均方差Table 1 Deviations of virtual stochastic variables

4.3 模型校准

本例中需要校准的参数有两类，其一是计算参数，其二是物理参数.参照验证和确认的顺序要求，先进行计算参数的校准，后进行物理参数的校准.因为新鲜材料和新鲜产品的试验数据比较丰富，拟基于新鲜产品的试验数据来校准计算参数，即首先根据工程任务对数值计算的准确性要求以及所耗费计算时间的承受能力，选择恰当的空间步长，然后将时间步长和人为粘性系数确定为校准量，以新鲜产品的试验结果为参照解，完成对时间步长和人为粘性系数的校准.物理参数的校准主要是对库存老化后材料参数e1和γ2的校准，需要用到库存产品的试验数据.校准后的计算参数和物理参数形成一组固定搭配，用于新对象的数值模拟预测.

按以下步骤开展数值模拟校准：

1）对计算方法、计算参数、物理参数和可调参数进行应用需求分析，确定校准量以及参照解的获取途径.本例只在计算参数和物理参数中选取校准量（选取结果见下文），并假定分析对象是复杂系统，参照解来自试验数据；

3）通过设计状态下模拟结果和5个试验结果的对比分析，得到优化的计算参数校准结果：初始网格宽度Δx＝0.1mm，时间步长Δt＝0.0016μs，人为粘性系数α＝1.5和β＝0.06，该粘性系数所对应的人为粘性模型为

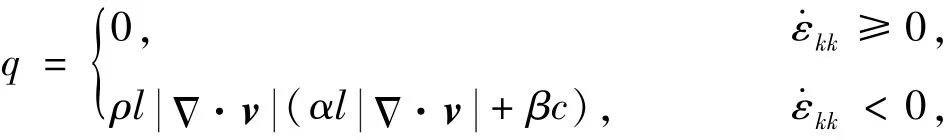
其中q为粘性压力，l为网格尺度，c为当地音速，Δ·v为速度的散度．计算参数校准以后，给出对应设计状态下的模拟结果Dm＆s，结果列于表2；

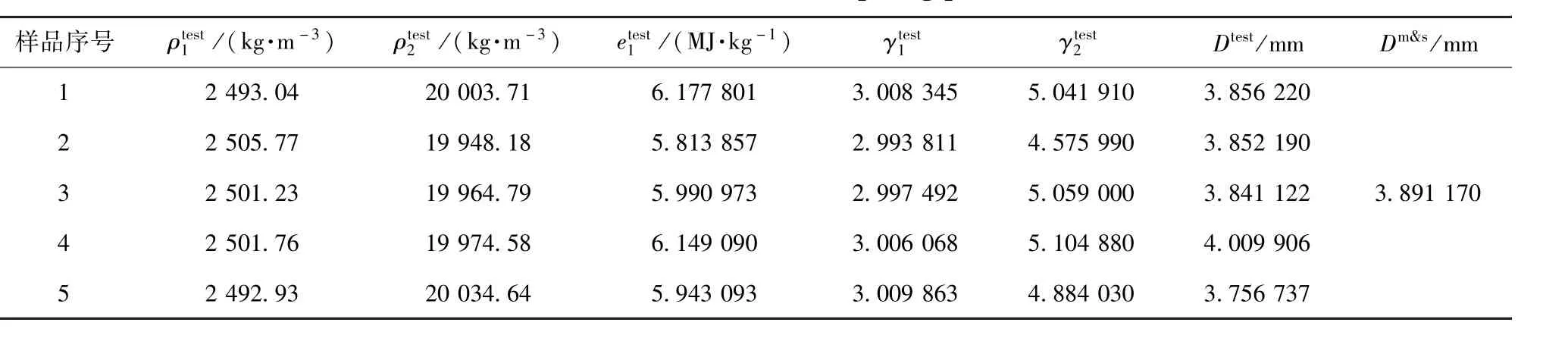
表2 试验结果和计算参数校准后的计算结果Table 2 Test data and M＆S result after com puting parameters calibrated

4）基于材料的老化模型以及库存期为10年、30年和50年的系统级试验与数值模拟的结果对比，校准物理模型参数.

老化模型给出的物理参数变化规律为

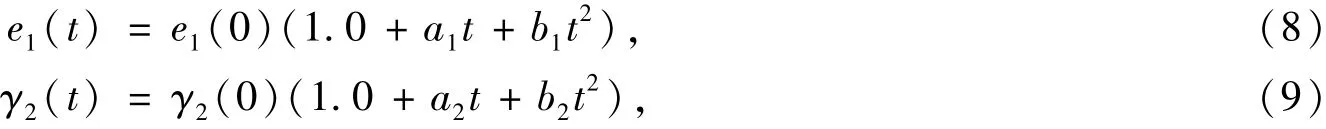
5）固化计算方法和各种校准参数的取值，完成数值模拟校准.

4.4 模型确认

在模型空间中，将库存时间从0年～50年的区域定义为确认域，确认试验分别对应0年、10年、20年、30年、40年和50年的库存时间，每个库存时间分别安排5次重复性试验，但只对应一个数值模拟结果.

依据公式（7）进行确认环节的不确定度量化，当置信度β＝0.95时，t（1－β）/2，ν＝t0.025，4＝2.7764，确认域内的不确定度量化结果见表3.

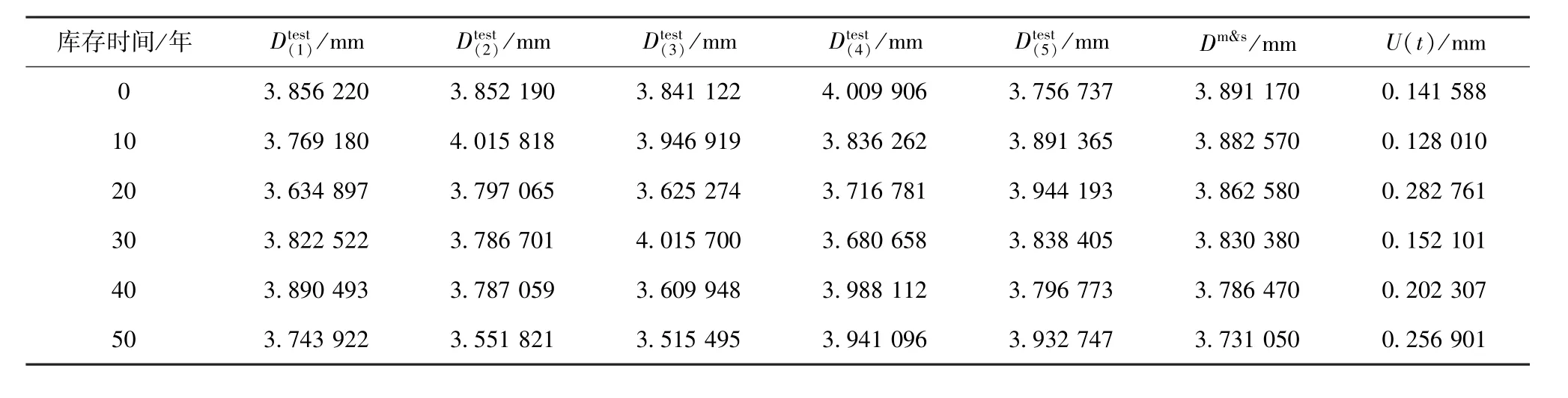
表3 确认域内的数值模拟不确定度Table 3 M＆S uncertainties in validation domain

4.5 应用域内不确定度的量化

在模型空间中，将库存时间大于50年的区域定义为应用域，该域内没有新的系统级试验.

为了量化式（3）的右端第一项，需要得到确认域内不确定度随库存时间的变化规律，本例用二次多项式来表达这个规律

根据表3中的信息，有

该超定方程的最小二范数解为

（a0，a1，a2）＝（1.415 7×10－1，2.6012×10－3，－1.3807×10－5）．

为量化式（3）的右端第二项，表4和表5分别列出了基于区间表达的不同库存期模型参数的不确定度以及系统响应量D对模型参数的偏导数（即敏感系数），其中偶然不确定度源自加工随机性导致的产品个体模型参数的随机变化，而认知不确定度源自建模者对模型参数母体均值的认知缺陷.由于80年库存期的材料级物理建模试验较少，又没有系统级试验用于模型校准，因此在建模方面比0年～50年库存期产品存在更多的认知不确定度，其中e1U增加了0.2MJ·kg－1，γ2U增加了0.2，即用式（8）－（10）求得的80年库存期模型参数，对模型参数的真值存在更大的偏离.

表4 模型参数的不确定度Table 4 Uncertainties ofmodel parameters

表5 系统响应量对模型参数的偏导数Table 5 Partial derivatives of system response to model parameters

对库存80年的产品，由模型参数不确定度增量传递到系统响应量上的不确定度为

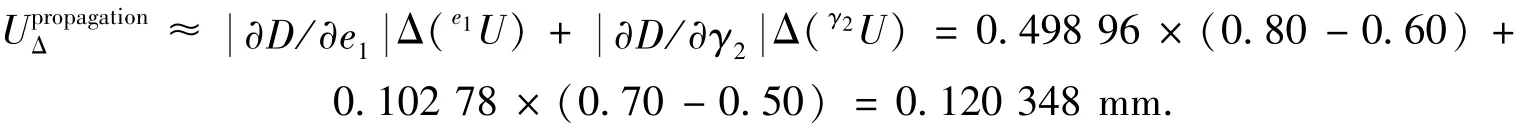
根据式（3），对应80年库存期的数值模拟不确定度为

假如将模型参数的认知不确定度整体传递到模拟结果中，则有

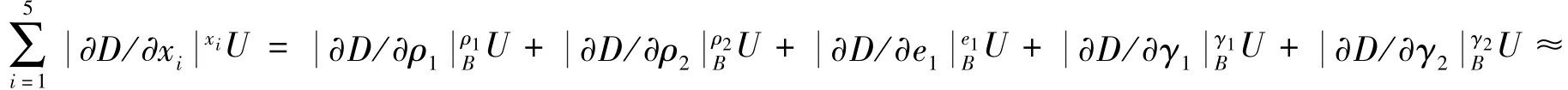
如果进一步将偶然不确定度也考虑在内，则仅由传递分析得到的数值模拟不确定度就高达0.92828mm，而且该结果还不能视为总的数值模拟不确定度.从这里可以看出，式（3）～式（7）所示的方法能有效利用试验校准对系统级认知不确定度的消减作用，过滤来自试验的偶然不确定度对量化结果的影响，合理地反映新对象数值模拟预测的不确定度.

4.6 不确定度量化方法的检验

为了检验上述方法的有效性，特意安排了应用域内对应80年库存期的试验.检验方法是，根据数值模拟和试验数据，直接由式（7）所示的对比方法对不确定度进行评定，如果式（13）的量化结果大于该评定结果且大得不多，则在一定程度上说明量化结果满足真值覆盖和最小化原则，量化方法正确有效.

试验方法同前，即根据真实模型确定80年库存期的设计参数，然后结合精确解和抽样方法给出5个重复性试验结果.数值模拟继续用式（10）所示的校准后的模型参数，并且数值模拟中模型参数的认知不确定度与虚拟实验中模型参数的偶然不确定度符合表4，即80年库存期与0～50年库存期相比，数值模拟所用的e1和γ2对真实模型的偏离分别增加了0.2MJ·kg－1和0.2，这两个增加的偏离在影响效果上均使D变大，能够很好地反映不确定度的叠加效应，突出检验效果.

表6为库存80年产品基于试验对比的数值模拟不确定度评定结果，其中数值模拟所采用的模型参数为ρ1＝2 500kg·m－3，ρ2＝20 000kg·m－3，e1＝5.4MJ·kg－1，γ1＝3.0，γ2＝6.02，e1和γ2的取值来自式（8）－（10），不确定度的评定仍采用式（7）.

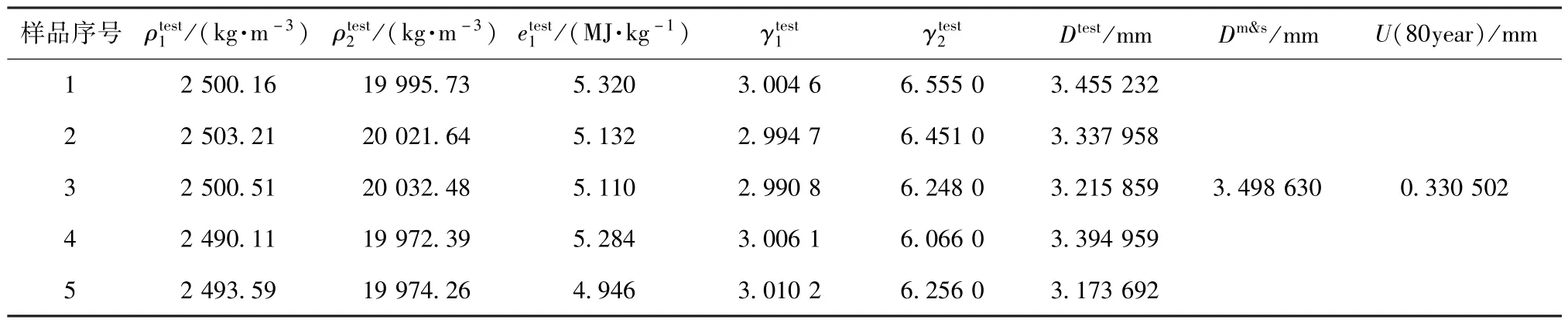
表6 基于试验对比的不确定度评定Table 6 Uncertainty assessment based on com parison w ith test data

由表6知，试验前用本文方法预测的数值模拟不确定度（0.381 65mm）稍大于试验后由对比分析得到的不确定度评定结果（0.330 502mm），说明该例中的不确定度量化是成功的.

5 结论

当一个新对象不能进行实物试验时，数值模拟预测及其不确定度量化结果就成为产品认证和评估的重要信息来源，而不确定度的传递分析往往被用作不确定度量化的常用手段.系统层级划分越细，输入的不确定因素也越多，仅靠传递分析则难以给出有实用价值的数值模拟不确定度.本文根据新对象的原型往往有一定试验数据的工程现实，利用数值模拟的试验校准能够大量消减认知不确定度的作用机制，提出了在没有新对象系统级试验的条件下综合利用校准后确认域对比信息和新增不确定度传递信息的数值模拟不确定度量化方法，案例表明该方法能够较好地遵循不确定度量化的真值覆盖原则和最小化原则，适用于新对象数值模拟预测的不确定度量化.

［1］ OberkampfW L，Roy C J.Verification and validation in science computing［M］.Cambridge University Press，2010：1－767.

［2］ Roy C J，OberkampfW L.A comprehensive framework for verification，validation，and uncertainty quantification in scientific computing［J］.Computer Methods in Applied Mechanics and Engineering，2011，200：2131－2144.

［3］ Ma Zhibo，Ying Yangjun，Zhu Jianshi.QMU certifyingmethod and its implementation［J］.Chinese Journalof Nuclear Science and Engineering，2009，29（1）：1－9.

［4］ Ma Zhibo，Li Haijie，Yin Jianwei，Huang Wenbin.Uncertainty quantification of numerical simulation for reliability analysis ［J］.Chinese Journal of Computational Physics，2014，31（4）：424－430.

［5］ Chen W，Baghdasaryan L，Buranathiti T，Cao J.Model validation via uncertainty propagation［J］.AIAA Journal，2004，42 （7）：1406－1415.

［6］ Helton J C.Conceptual and computational basis for the quantification of Margins and uncertaity［A］.Sandia Report，SAND2009－3055.

［7］ Liu Quan，Wang Ruili，Lin Zhong，Wen Wanzhi.Uncertainty quantification for JWL EOS parameters in explosive numerical simulation［J］.Chinese Journal of Explosion and Shock Waves，2013，33（6）：647－654.

［8］ Ma Zhibo，Zheng Miao，Yin Janwei，et al.Quantification of uncertainties in detonation simulations［J］.Chinese Journal of Computational Physics，2011，28（1）：66－74.

［9］ Higdon D，Kennedy M，et al.Combining field observation observations and simulation for calibration and prediction［J］. SIAM Journal of Scientific Computing，2004，26：448－466.

［10］ Helton J C.Uncertainty and sensitivity analysis in the presence of stochastic and subjective uncertainty［J］.Journal of Statistical Computation and Simulation，1997，57：3－76.

［11］ Babuska I，Nobile F，Tempone R.A systematic approach tomodel validation based on bayesian updates and prediction related rejection criteria［J］.Computer Methods in Applied Mechanics and Engineering，2008，197（29/32）：2517－2539.

Uncertainty Quantification of Numerical Simulations Subjected to Calibration

MA Zhibo1，YIN Jianwei1，LIHaijie2，LIU Quan1
（1.Institute of Applied Physics and Computational Mathematics，Beijing 100088，China；
2.Electromechanical Product Research and Development Center，Changsha 410100，China）

Propagation analysis often overrate uncertainty of numerical simulation，especially asmany uncertain inputs exist.Taking advantage of the reality that calibration can reduce epistemic uncertainty of system⁃level numerical simulation，amethod for uncertainty quantification is offered synthetically using comparison information based on available testdata and additional propagation information of modeling and simulation.An example with virtual test is displayed in which themethod is demonstrated and validated.

numerical simulation；uncertainty quantification；calibration；reliability certification

O242.1

A

2014－08－12；

2014－12－24

国家自然科学基金（11371066）、装备预先研究（51319010207）及中国工程物理研究院科学技术发展基金（2012B0102010，2013A0101004）资助项目

马智博（1963－），男，博士，研究员，主要从事计算物理和可靠性工程研究，E⁃mail：mazhibo＠iapcm.ac.cn

Received date： 2014－08－12；Revised date： 2014－12－24