Salt and pepper noise removal in surveillance video based on low-rank matrix recovery

Yongxia Zhang,Yi Liu,Xuemei Li(),and Caiming Zhang,2

©The Author(s)2015.This article is published with open access at Springerlink.com

Salt and pepper noise removal in surveillance video based on low-rank matrix recovery

Yongxia Zhang1,Yi Liu1,Xuemei Li1(),and Caiming Zhang1,2

©The Author(s)2015.This article is published with open access at Springerlink.com

This paper proposes a new algorithm based on low-rank matrix recovery to remove salt& pepper noise from surveillance video.Unlike single image denoising techniques,noise removal from video sequences aims to utilize both temporal and spatial information.By grouping neighboring frames based on similarities of the whole images in the temporal domain,we formulate the problem of removing salt& pepper noise from a video tracking sequence as a lowrank matrix recovery problem.The resulting nuclear norm and L1-norm related minimization problems can be efficiently solved by many recently developed methods.To determine the low-rank matrix,we use an averaging method based on other similar images.Our method can not only remove noise but also preserve edges and details.The performance of our proposed approach comparesfavorably to thatofexisting algorithms and gives better PSNR and SSIM results.

multimedia computing;noise cancellation; signal denoising;sparse matrices;video signal processing;video surveillance

1 Introduction

Due to the popularity of webcams and mobile phone cameras,image denoising is still an important problem of interest.Given the high speed of video capture,video data is more likely to be noisy than single images.Clearly,a single-image denoising method can be used to remove noise from video databy processing each frame independently.However, an ideal video denoising algorithm should utilize information in both temporal and spatial domains to take advantage of the high temporal redundancy in video.

Most of papers on video denoising concentrate on i.i.d.Gaussian white noise[1-6].However salt& pepper noise is also common in video,especially surveillance video.It can be introduced during signalacquisition orbe dueto biterrorsin transmission.Salt&pepper noise corrupts the signal by replacing the original pixel value with either the maximum or minimum gray level value;it severely impacts the accuracy and efficiency of information retrieval from such signals.Many existing algorithms for removing salt&pepper noise from sequences use a single-image denoising method on each frame of video[7].Such methods do not take advantage of the information in the temporal domain.

Patch-based non-local schemes are promising and provide very impressive denoising results,but the patch size must be selected carefully via many experimental tests-it depends on the object to be dealt with and the noise level.Furthermore,this method groups many patches based on similarity, which should be evaluated by some measurement, butthismay bedegraded bytheimpactof noise.Thirdly,one pixel may belong to different patches grouped in many different stacks and it may be considered many times.The denoised result is found by aggregating all the values calculated in different groups and one frame may need thousands of calculations to obtain the denoised data,so the process is wasteful and the cost of computation is very high.

This paper proposes a robust video denoisingmethod capable of removing salt&pepper noise from video data using information in both spatial and temporal domains.The proposed method is similar to patch-based schemes.Unlike existing methods, our algorithm uses the whole frame as a patch and takes neighboring frames as similar patches.The basic idea is to convert the problem of removing noise from the stack of images to a low-rank matrix recovery problem,which can be solved by minimizing the nuclear norm(L1-norm of all singular values)and L1-norm of the matrix with linear constraints.Our low-rank matrix recovery based video denoising approach combined with median filtering can remove salt& pepper noise efficiently and give better peak signal-to-noise ratio(PSNR)and structural similarity(SSIM)results,as shown later.

The main theoretical contribution of this paper is that the original data in neighboring frames form a low-rank matrix because of their internal similarity of structure,and the denoising problem can be formulated as low-rank matrix recovery.Entire imagesareprocessed instead ofsmallpatches which brings many benefits.Firstly,by taking the whole image as a patch,the size of patch is fixed, and need not be chosen by the user according to video data and noise level.Secondly,there is no need to choose an appropriate criterion to evaluate similarities between patches which may be affected by noise or patch size,as neighboring frames in surveillance video have high similarity due to temporal redundancy.Last but not least, the denoised results can be obtained with less computation.

1.1 Related work

There have been many research papers on image denoising.In this section,we only discuss the most closely related denoising techniques.

Most of these video denoising methods assume that noise is additive i.i.d. Gaussian white noise.Generally,these algorithms do not work well when the video sequences are corrupted by some other types of noise such as salt&pepper noise.Of course,there have been many research works on removing salt&pepper noise from a single image[7-11].One of the common and simplest methods of removing salt&pepper noise is the median filter (MF)along with its variants.However,traditional MF methods are usually applied indiscriminately acrossthewholeimagemodifyingboth noise corrupted pixels and noise-free pixels which results in blurred and distorted images.To overcome this drawback,many decision based median filters have been proposed[9-11].Pixels corrupted by noise are firstly detected by rules and replaced by the median of a local window,or some variant.The modified decision based asymmetric trimmed median filter (MDBUTMF)[11]replaces the noisy data with the median value when its neighbor pixels are not all corrupted,or by the mean otherwise.This scheme is good because the noise-free pixels are left unchanged, protecting sound regions to some extent.However, the replacement methods in these algorithms cannot preserve all image features,especially edges.In Ref.[8],the directional multi-pass median filter (DMPMF)is applied repeatedly to remove noise and then directional filtering is applied to preserve the details and edges in the restored image.In Ref.[7], the adaptive decision based median filter(ADBMF) is used to remove salt&pepper noise from video by applying this filter to each frame as single image without considering information in the temporal domain.The adaptive temporal averaging(ATA) algorithm[2]takes advantage of the similarity of frames in the temporal domain to remove Gaussian noise from image sequences by averaging similar neighboring frames.

In recent years,patch-based non-local schemes have been proposed as a promising approach with very impressive results [1,3-6,12-14].These methods have a similar framework but differ in details.In general,they group similar patches into stacks and then apply collaborative filtering.The famous BM3D algorithm[12]may be taken as a representative example,and is one of the best denoising methods for removing Gaussian white noise with big PSNR values.In BM3D,similar small patches are grouped in a stack by block matching to form a 3D array.Then each 3D block stack is shrunk in the 3D transform domain using wavelet shrinkage or a Wiener filter.The denoised image is aggregated from denoised patches after inverse 3D transformation.BM3D applies grouping and collaborative filtering twice,so the PSNR value is increased.The result can be further improved byiteratively repeating this process.The idea of sparse representation using a patch dictionary has also been applied to video denoising[5,14],where the denoised image patches are found by seeking the sparsest solution in a patch dictionary.The idea of low rank has also been used to remove noise from video data [15].In Ref.[15],similar small patches are grouped and reformed as a matrix,then implausible items are removed and rules are used to preserve only the most reliable data.Finally the video denoising problem is formulated as low-rank matrix completion with many elements missing.In all such methods, denoised frame images are aggregated from denoised patches.

Image denoising methods can be applied on video sequences directly by denoising each of the frames separately.But surveillance video sequences usually have very high temporal redundancy which meansneighboringframeshavehigh similarity in structure which should be effectively used forbetterperformance[2,7,15].Patch-based schemes can also be applied to video sequences, but unlike in single image denoising,the block matching process is not only applied within each image to which the referenced patch belongs,but also within neighboring frames.The concept of BM3D can be expanded to video denoising[1] by using predictive search block matching over time and collaborative Wiener filtering on patch stacks.However,algorithms for removing salt& pepper noise from image sequences do not make best use of temporal redundancy of video.

1.2 The motivation and our work

Most existing video denoising algorithms assume the data is corrupted by i.i.d.Gaussian white noise,and as a result, they do not work well when other types of noise are present such as salt &pepper noise-the performance of a denoising method ishighly dependenton how wellthe noise in the data fits the statistical noise model assumed by the method. However,salt&pepper noise is common in surveillance video,and may be introduced during the signal acquisition stage or arise due to bit errors in transmission.Of course,there are many approaches to remove salt &pepper noise from a single image,and they can be expanded to video denoising simply by dealing with each frame independently.In this way,the high temporal redundancy in video sequence is ignored and wasted.Furthermore,median filtering and its variants,even in the most popular algorithms for removing salt&pepper noise,may not remove noise completely,and may also result in artifacts or blurring.These observations have inspired us to develop a robust denoising algorithm capable of removing salt&pepper noise from the given video data using the information in both temporal and spatial domains.

In traditional patch-based schemes,small patches are used with a fixed size determined by experiment; this size depends on the subject and noise level.Block matching is applied to pick up similar patches to form stacks,which may be disturbed by the noise.At the same time,one pixel may belong to different patches and may be processed many times.The whole image is determined by aggregating the denoised patches.This approach makes the algorithm complicated and gives it a high cost.This inspired us to take the whole image as a patch and similar neighboring frames as stacks,without using a patch matching process and aggregating to get the final result.Since the neighboring frames in a video have similar underlying image structures,the noiseless version of these images in a stack lies in a low dimensional subspace.If the stack of images is rearranged as a matrix,it becomes a noisy version of a low-rank matrix with many noisy elements.In consequence,the problem of denoising image stacks is converted to the problem of recovering a low-rank matrix from a noisy observation.

Recently there has been great progress in solving the problem of low-rank matrix recovery.As the rank of a matrix is not a convex function,the nuclear norm of the matrix is used to approximate it,which leads to a convex minimization problem, with many efficient solution methods available(e.g., [16-19]).In our implementation,we use the inexact ALM algorithm to solve low-rank matrix recovery by minimizing the nuclear norm and L1-norm of the matrix with linear constraints(see Ref.[16]for more details).

The structure of the paper is as follows.In Section 2,we describe our formulation of video denoising based on low-rank matrix recovery,and discuss the details of our proposed method.Experimentalevaluation of the proposed method is given in Section 3.Section 4 summarizes and concludes the paper.

2 Proposed methodology

2.1 Problem formulation

The image denoising task is to recover a clear image f from the given noisy image g,which can be generally formulated as

where n is the noise.Extending the above model based on image patches,we may reformulate it as

i.e.,G=F+N,where F is the matrix composed of clean image patches fi,N is the matrix of noise corresponding to matrix F,and G is the matrix of noisy image patches gi.These three matrices have the same size.In BM3D,these matrices are three dimensional and formed by similar patches within one group,while in other patch-based algorithms[13],these matrices are two dimensional, based on columns after reshaping each patch as a vector.In our proposed algorithm,images are reshaped as a vector to form the two-dimensional degraded matrix.

To exploit the temporalredundancy in a surveillancevideo,wetakeneighboringframes having homogeneous underlying image structures as similar patches,so these patches lie in a low dimensional subspace.If we rearrange these images as a matrix,such a matrix becomes a noisy version of a low-rank matrix with many noisy elements.In this way,the problem of video denoising can be formulated as recovering a low-rank matrix from an observed degraded matrix.

An r×cmatrix M haslow rank ifits rank(rank(M))is much smaller than its smaller dimension,i.e.,rank(M)≪ min(r,c).As noted in Ref.[19],the bigger a matrix M is,i.e.,the larger min(r,c),the more likely the low-rank property is to be preserved.Neighboring frames in a video have high similarity except for small shifts for temporal redundancy.However the longer the time span between a set of frames of video,the lower the similarity,so the rank of matrix G representing the images is larger.To ensure higher similarity and sufficient information,for every frame we use n/2 earlier frames and n/2 later frames.In this way, each frame is processed n times and the denoised frame can be obtained by weighted averaging of n results.Thus,the proposed method has two stages.In the first stage,we split the sequence into groups and use a simple averaging method to provide further similar images in each group,forming the matrix G.The second stage reformulates the denoising process as recovery of a low-rank matrix F from a degraded matrix G with the constraint that N=G−F is sparse,by minimizing rank(F)+‖N‖0.

Low-rank matrix recovery aims to recover a lowrank matrix F from G,subjected to the constraint that G=F+N and the error N is sparse.There are many papers on solving this problem[14,16-18].In this paper,we adopt the inexact ALM algorithm (introduced in Section 2.3)to solve the low-rank matrix recovery problem because of its simplicity of implementation and computational efficiency.

2.2 Image groups and forming the degraded matrix

Toensurehigh similarity between theimages processed in one group,the video sequence with K frames is divided into K groups in which each frame is included in more than one group,and all of the frames in one group are denoised together via a lowrank matrix recovery problem.

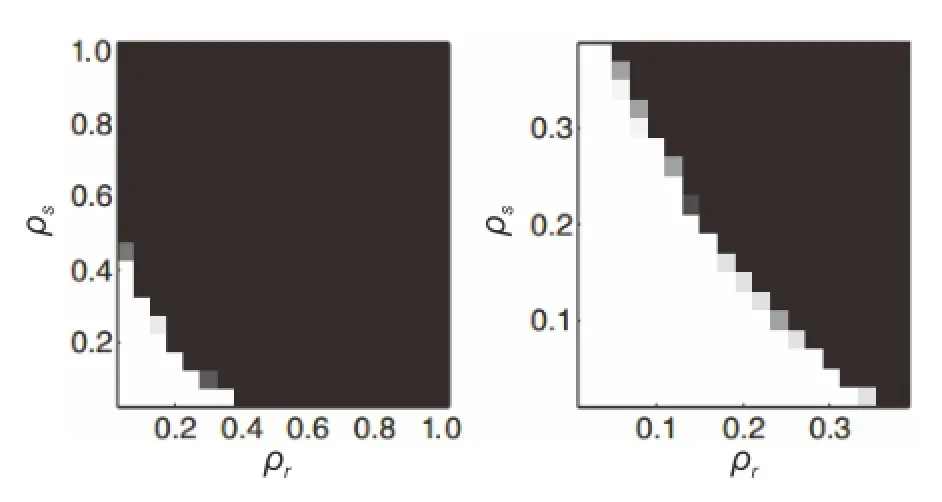
Fig.1 Phase transition with respect to rank and fraction of noisy entries[18].

In Ref.[18],the circumstances under which the low-rank matrix can be recovered correctly are analysed.For a low-rank matrix M0with the size of r×c,M is the observed matrix for M0with many corrupted items.We let ρr=rank(M0)/min(r,c) and the fraction of noisy entries in matrix M is ρs.If the recoveredsatisfies0.01,the low-rank matrix recovery is considered to be successful.Figure 1 right shows detail of Fig.1 left,with white denoting perfect recovery,and black denoting failure.As shown in Fig.1,when ρr＜0.4 and the value of ρsis such that(ρr,ρs)is located in the white region,the low-rank matrix recovery problem can be solved successfully.Otherwise,the recovered matrix may preserve some dirty entries.In the problem of video denoising,if the noise level is high,which means that ρsis large and(ρr,ρs) does not satisfy the condition above,the recovered imageswillbe stillnoisy.In orderto avoid this phenomenon,we do not deal with the raw data immediately like BM3D algorithm.Instead, a modified decision based unsymmetric trimmed median filter(MDBUTMF)[11]is used to firstly decrease the value of ρs.MDBUTMF only changes noisy pixels with values 0 or 255,and replaces the value with the mean or median of elements in a local window based on the neighbor’s pixel values in the selected window.We use a simple averaging method to supply further similar images from intermediate images processed by MDBUTMF to form the observed matrix G and lower the value of ρr.Given m images{Ii}m,we can get m similar images{Si}mgiven by

In the same way,we can get 2m images from{Si}m]by Eq.(3).The more times the process is applied,the more images can be obtained.The degraded matrix of each group consists of column vectors formed by reshaping the images in the group and the similar images generated by the averaging method.

2.3 Denoising the image matrix

For each group of images,we use MDBUTMF and the averaging method to generate further similar images and form the image matrix G.As discussed in Section 2.1,F is recovered from the degraded observation matrix G by minimizing the rank of matrix F and the L0-norm of matrix N with the constraint G=F+N.This optimization problem may be reformulated as

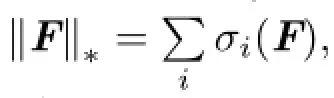
There are many available efficient algorithms to solve the above minimization problem.The ALM method which combines the Lagrange multiplier (LM)method with a multiplier penalty function operates on the augmented Lagrangian:

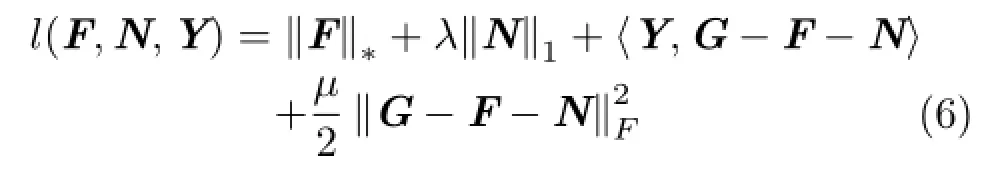
where Y is a Lagrange multiplier matrix,〈A,B〉= traceis the Frobenius norm, andµis the penalty factor updated in the iterations. The inexact ALM algorithm(see Ref.[16]for more details)is the ALM method used in this paper for its simplicity of implementation.

3 Experiments

In thissection,we evaluate the performance oftheproposed method onmanysurveillance video samplescorrupted by differentlevelsof salt&pepper noise.All video data used in the experimentscan bedownloaded from http:// media.xiph.org/video/derf/.A wide range of noise ratios varying from 10%to 50%in increment of 10% have been used to study the efficacy of the proposed methodology.Thecomparative analysisofthe results obtained by the proposed method and those of published techniques is presented in terms of peak signal-to-noise ratio(PSNR)that measures the degree of closeness between the restored and original images,and structural similarity(SSIM)which measures the similarity of structural information between two images,with a high consistency with human visual perception.PSNR(dB)is defined as

SSIM is defined as

The bigger the PSNR and SSIM values are,the more similar are the denoised image and clean image.Since the quality of an image is subjective, the denoising efficacy of the method for salt&pepper noise is also judged by visual inspection.

In the experiment,we use even prolongation of the video and denoise each key frame of test surveillance video sequence using information from n=4 neighbor frames,with neighbours from both sides.In other words,five frames are processed at a time;most frames are used five times except for the first and last two frames.As the fraction of corrupting data in matrix G is unknown,to make sure the low-rank matrix recovery problem can be solved perfectly,we should make the value ρsas small as possible.Taking into account the computer’s capability and the efficiency of the algorithm,we expand the matrix G with the averaging method five times so that ideally ρr=0.03.

To demonstrate the advantages of our proposed method,we compare results with two classes of algorithms.Firstly,to show the importance of information in the temporal domain,we compare our method with other recent single frame denoising algorithms:MDBUTMF[11],DMPMF[8],and ADBMF[7];they focus on removing salt&pepper noise from video frame by frame.The visual quality can be evaluated in Figs.2(c)-2(k).It is clear that ADBMF and MDBUTMF methods do not remove all of the noise.DMPMF can remove most of the noise but some artifacts are produced and much detail information is lost.The denoised image provided by our method is clearer and closer to the noise-free frame,with more details and structural information than the other methods.It achieves the highest PSNR value.

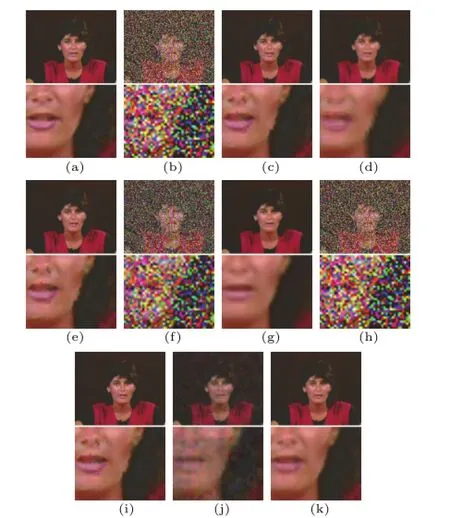
Fig.2 Miss America sequence with 40%salt&pepper noise: (a)noise-free frame;(b)noisy frame,PSNR=8.58; (c)frame denoised by ADBMF[7],PSNR=36.56;(d)frame denoised by DMPMF[8],PSNR=33.77;(e)frame denoised by MDBUTMF[11],PSNR=35.86;(f)frame denoised by VBM3D without salt&pepper noise pre-processing,PSNR=10.30;(g) frame denoised by VBM3D with MDBUTMF pre-processing, PSNR=32.30;(h)frame denoised by ATA[2],PSNR=8.63; (i)framedenoised by ATA [2]with MDBUTMF preprocessing,PSNR=35.73;(j)frame denoised by the method in Ref.[15],PSNR=25.53;and(k)frame denoised by our method, PSNR=37.88.

Secondly,we also compare our method with patchbased non-local denoising schemes:the VBM3D method[1]which is a typical representative of patchbased non-local algorithms(we use the authors’executable code from their website),the method in Ref.[15],and ATA[2].VBM3D and ATA methods only consider Gaussian white noise and do not work well on salt&pepper noise,as shown in Figs.2(f)and 2(h).Using pre-processing to remove salt&pepper noise,the result from the method is greatly improved,as shown in Figs.2(g)and 2(i).Thus,we should compare to the VBM3D method with salt&pepper noise pre-processing.The method in Ref.[15]can remove most of the noise but some detail information is lost.The denoised image produced by our method is clearer and closer to the noise-free frame with more detail and structural information than results from other methods.Further examples are shown in Figs.3-6 with different noise levels.Image frames and close ups are shown in the first and second rows.These figures show:(a)noise-free frame;(b)noisy frame; (c)frame denoised by ADBMF[7];(d)frame denoised by DMPMF[8];(e)frame denoised by MDBUTMF[8];(f)frame denoised by VBM3D withMDBUTMF prep-rocessing;(g)frame denoised by ATA[2]with MDBUTMF processing;(h)frame denoised by the method in Ref.[15];and(i)frame denoised by our method.Values of PSNR and SSIM obtained by the proposed method and comparison to state-of-the-art algorithms are listed in Table 1 and Table 2,respectively.There is little improvement when VBM3D is applied after MDBUTMF preprocess.The ATA algorithm is averaging most similar frame images,that is to say,sometimes,ATA may take more existing images in the sequence and get a better result.In general,it is obviouse that our method increases the PSNR and SSIM values from MDBUTMF obviously and gets the higher values even in high noise level than the other methods.

Fig.3 Carphone sequence with 10%salt&pepper noise.

Fig.4 Container sequence with 20%salt&pepper noise.

Fig.5 Tempete sequence with 30%salt&pepper noise.

Fig.6 Akiyo sequence with 50%salt&pepper noise.

4 Conclusions

In thispaper,wehaveproposed an efficient algorithm to remove salt&pepper noise from surveillance video sequences.By formulating the video denoising problem as a low-rank matrix recovery problem,our proposed algorithm uses neighboring frame images to form a similar patch stack without patch matching.The effectivenessof our proposed algorithm is validated in various experiments.The method proposed in this paper can also be applied to images continuously sampled from the same scene.However,when dealing with dynamic video sequences,rapid changes of location between frames may result in a little blurring.In future,we hope to study motion preservation technologies and combine them with the current ideas to remove noise from video data of dynamic scenarios.

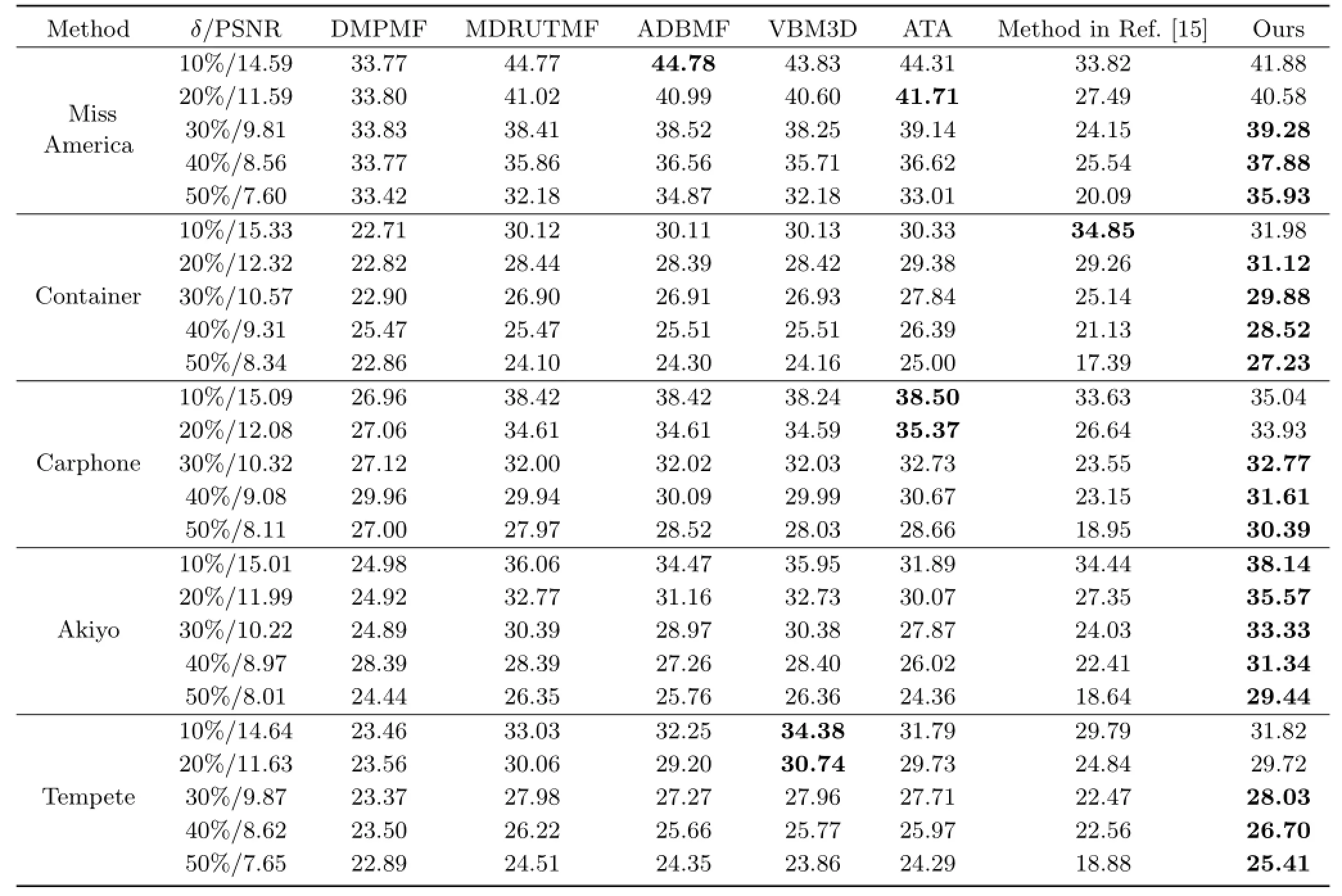
Table 1 PSNR values of video sequences denoised using our method and other methods

Acknowledgements

The authors would like to thank the referees for their valuable suggestions which significantly improved the paper.The original surveillance videos are from http://media.xiph.org/video/derf/.This work was supported by the National Nature Science Foundation of China(Nos.61332015,61373078, 61272245,and 61272430),and NSFC Joint Fund with Guangdong(No.U1201258).

Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use,distribution,and reproduction in any medium,provided the original author(s)and the source are credited.

[1]Dabov,K.;Foi,A.;Egiazarian,K.Video denoising by sparse 3D transform-domain collaborative filtering. In: 15th European Signal Processing Conference,145-149,2007.

[2]Bartov˘cak,D.;Vranki´c,M.Video denoising based on adaptive temporal averaging.Engineering Review Vol.32,No.2,64-69,2012.

[3]Zlokolica,V.;Pizurica,A.;Philips,W.Waveletdomain video denoising based on reliability measures. IEEE Transactions on Circuits and Systems for Video Technology Vol.16,No.8,993-1007,2006.

[4]Protter,M.;Elad,M.Image sequence denoising via sparseand redundantrepresentations.IEEE Transactions on Image Processing Vol.18,No.1,27-35,2009.

[5]Cheong, H.-Y.; Tourapis, A.M.; Llach, J.; Boyce,J.Adaptive spatio-temporal filtering for video denoising.In:2004 International Conference on Image Processing,Vol.2,965-968,2004.

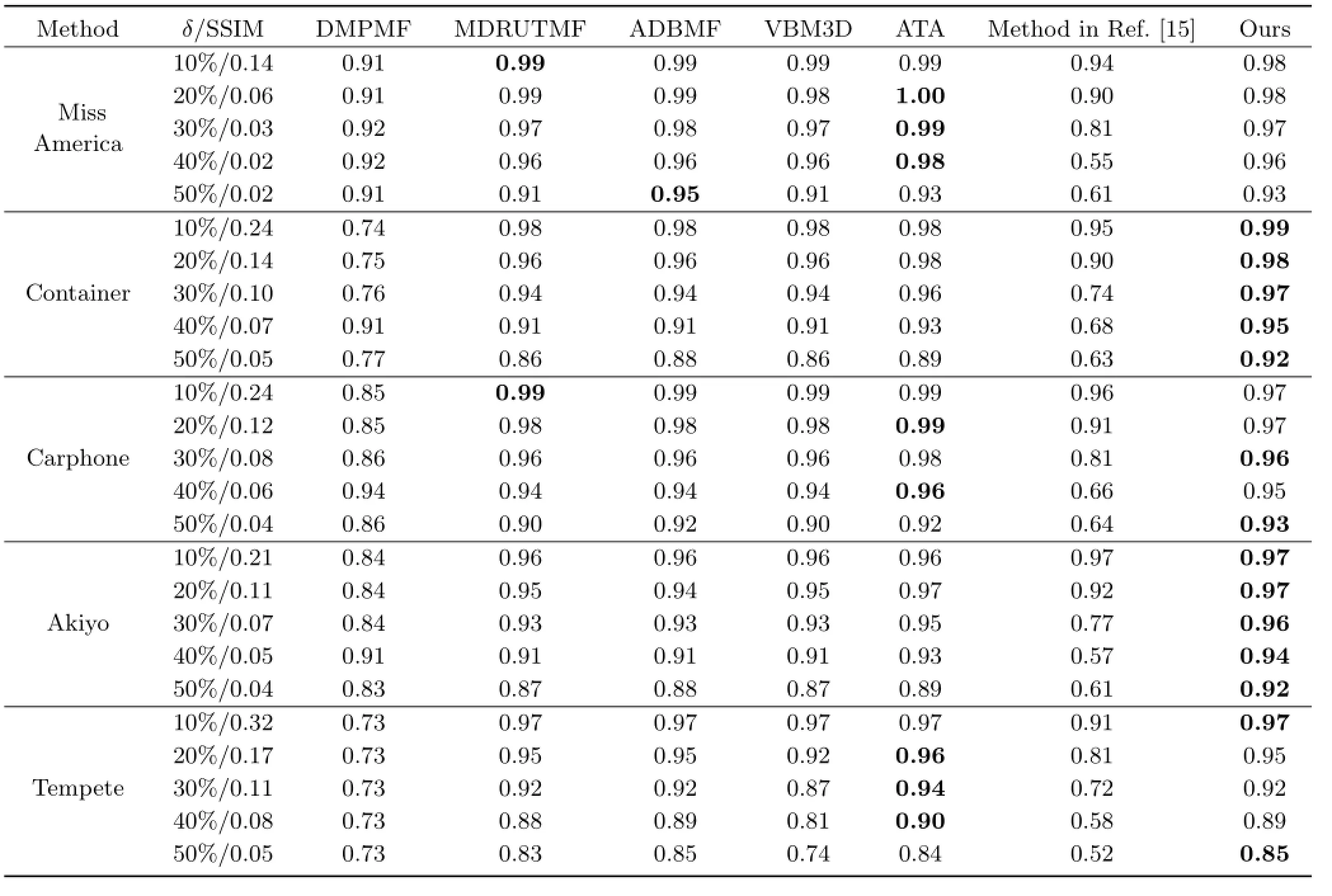
Table 2 SSIM values of video sequences denoised using our method and other methods

[6]Chen,J.;Tang,C.-K.Spatio-temporalMarkov random field for video denoising.In:IEEE Conference on Computer Vision and Pattern Recognition,1-8, 2007.

[7]Veerakumar,T.;Esakkirajan,S.;Vennila,I.Salt and pepper noise removal in video using adaptive decision based median filter.In:2011 International Conference on Multimedia,Signal Processing and Communication Technologies,87-90,2011.

[8]Vajpai,J.;Mehta,S.Directional multi-pass median filter for impulse noise reduction.In:2013 Fourth National Conference on Computer Vision,Pattern Recognition,Image Processing and Graphics,1-4, 2013.

[9]Chan,R.H.;Ho,C.-W.;Nikolova,M.Salt-and-pepper noise removal by median-type noise detectors and detail-preserving regularization.IEEE Transactions on Image Processing Vol.14,No.10,1479-1485,2005.

[10]Srinivasan,K.S.;Ebenezer,D.A new fast and efficient decision-based algorithm for removal of highdensity impulse noises. IEEE Signal Processing Letters Vol.14,No.3,189-192,2007.

[11]Esakkirajan,S.;Veerakumar,T.;Subramanyam, A.N.;PremChand,C.H.Removal of high density salt and pepper noise through modified decision based unsymmetric trimmed median filter. IEEE Signal Processing Letters Vol.18,No.5,287-290,2011.

[12]Dabov,K.;Foi,A.;Katkovnik,V.;Egiazarian, K.Image denoising by sparse 3-D transform-domain collaborative filtering.IEEE Transactions on Image Processing Vol.16,No.8,2080-2095,2007.

[13]Dong,W.;Zhang,L.;Shi,G.;Li,X.Nonlocally centralized sparse representation for image restoration.IEEE Transactions on Image Processing Vol.22,No.4,1620-1630,2013.

[14]Mairal,J.; Bach, F.; Ponce,J.; Sapiro,G.; Zisserman,A.Non-local sparse models for image restoration.In: 2009 IEEE 12th International Conference on Computer Vision,2272-2279,2009.

[15]Ji,H.;Liu,C.;Shen,Z.;Xu,Y.Robust video denoising using low rank matrix completion.In:2010 IEEE Conference on Computer Vision and Pattern Recognition,1791-1798,2010.

[16]Lin,Z.;Chen,M.;Ma,Y.The augmented Lagrange multiplier method for exact recovery of corrupted lowrank matrices.arXiv:1009.5055,2010.

[17]Toh,K.-C.;Yun,S.An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems.Pacific Journal of Optimization Vol.6,No.3,615-640,2010.

[18]Wright,J.;Ganesh,A.;Rao,S.;Peng,Y.;Ma, Y.Robustprincipalcomponentanalysis: Exact recovery of corrupted low-rank matrices by convex optimization.In: Advances in Neural Information Processing Systems 22,2080-2088,2009.

[19]Cand`es,E.J.;Li,X.;Ma,Y.;Wright,J.Robust principal component analysis?Journal of the ACM (JACM)Vol.58,No.3,Article No.11,2011.

Yongxia Zhang received the B.S. degree from Qilu University of Technology,Jinan,China,in 2011.She is currently working toward the Ph.D. degreein the SchoolofComputer Science and Technology, Shandong University,Jinan,China.Her research interests include computer vision,image processing,and machine learning.In particular,she focuses on the problems of image and video denoising and image segmentation.

Yi Liu received the M.S.degree in electronic information science and technology from the Information Engineering College, Shandong University in 1998,the Ph.D.degree in computer software and theory of computer science and technology from Shandong University in 2006.She was a postdoctoral fellow of computer science and technology in Peking University in 2008.Currently,she is a professor in the School of Computer Science and Technology,Shandong University.Her research interests include wavelets,image signal processing,and pattern recognition.

XuemeiLi received the M.S.and Ph.D. degrees from Shandong University, Jinan, China, in 2004 and 2010,respectively.She is currently an associate professorin Schoolof Computer Science and Technology, Shandong University.She is engaged in research on geometric modeling,CAGD, medical image processing,and information visualization.

Caiming Zhang is a professor and doctoral supervisor of the School of Computer Science and Technology, Shandong University.He received the B.S.and M.E.degrees in computer science from Shandong University in 1982 and 1984,respectively,and a D.E.degree in computer science from the Tokyo Institute of Technology,Japan,in 1994.From 1997 to 2000,Dr.Zhang has held the visiting position in the University of Kentucky,USA.His research interests include CAGD,CG,information visualization,and medical image processing.

1School of Computer Science and Technology, Shandong University,Jinan 250101,China. E-mail: xmli@sdu.edu.cn().

2Shandong University ofFinance and Economics, Shandong Provincial Key Laboratory of Digital Media Technology,Jinan 250014,China.

Manuscript received:2014-10-10;accepted:2015-01-26