Edge-preserving image decomposition via joint weighted least squares

Pan Shao,Shouhong Ding,Lizhuang Ma(),Yunsheng Wu,and Yongjian Wu

©The Author(s)2015.This article is published with open access at Springerlink.com

Edge-preserving image decomposition via joint weighted least squares

Pan Shao1,Shouhong Ding1,Lizhuang Ma1(),Yunsheng Wu2,and Yongjian Wu2

©The Author(s)2015.This article is published with open access at Springerlink.com

Recent years have witnessed the emergence of image decomposition techniques which effectively separate an image into a piecewise smooth base layer and several residual detail layers.However,the intricacy of detail patterns in some cases may result in side-effects including remnant textures,wronglysmoothed edges, and distorted appearance.We introduce a new way to construct an edge-preserving image decomposition with properties of detail smoothing,edge retention,and shape fitting.Our method has three main steps: suppressing highcontrast details via a windowed variation similarity measure,detecting salient edges to produce an edgeguided image,and fitting the original shape using a weighted least squares framework.Experimental resultsindicate thatthe proposed approach can appropriately smooth non-edge regions even when textures and structures are similar in scale.The effectiveness of our approach is demonstrated in the contexts of detail manipulation,HDR tone mapping, and image abstraction.

detail suppression;edge extraction;edgepreserving decomposition;shape recovery

1 Introduction

Many natural photos and artworks include various well-structured objects with rich visual information. These images usually contain distinctive texture elements as well as complex structures. Many current applications incomputational photography call for decomposition of an image into a piecewise smooth base layer plusoneormoredetaillayerswith different scales.Appropriate manipulation of these layers separately provides a basis for meeting the needs of a wide range of applications such as image fusion and enhancement[1,2],tone mapping and transfer[3,4], and image-based editing[5,6].

The paramount problem of image decomposition techniques is to obtain the base layer via some coarsening operations,following which detail layers can be extracted.During these operations, proper determination of edge elements and detail elements is crucial,since edges should be preserved while details require smoothing.Numerous edgepreserving smoothing algorithms exist which aim to suppressorcapturedetailsin images.As traditional linear filters[7]are known to produce halo artifacts near edges,several non-linear smoothing filters[8-11]have been devised to mitigate this shortcoming.Common approaches[12-16]depend on gradient magnitudes or brightness differences to distinguish edges from details.Therefore,they lead to unsatisfactory image decomposition when textures and structures are similar in scale.Some studiesstrive to characterize detailsby rapid oscillations between local minima and maxima[17]or by relative total variation[18].They have difficulties in handling images with complex content despite producing superb results in certain cases.The drawbacks of these techniques can be generalized as: detail residue,edge collapse,and shape distortion.

We propose a noveledge-preserving image decomposition framework via joint weighted least squares that effectively smooths the non-edge regions while fitting the overall appearance.Taking the weighted least squares(WLS)mechanism[14]as abridge,we successively remove high-contrast details, extract salient edges,and finally recover the initial shape.The detail suppression stage is based on the key observation that the gradients of details always differ widely in small local regions while those of edges usually point in similar directions.This allows us to repress the gradients of details to a lower magnitude than those of edges,after which use of edge detection methods becomes feasible to separate edges from details.The shape recovery stage strives to obtain the coarse base layer which,meanwhile,is analogous to the original image.

The remainder of this paper is organized as follows.In the next section,we discuss the related work on base-detail decomposition and explain the causes of some shortcomings in performance.In Section 3, we elaborate our edge-preserving decomposition framework via joint weighted least squares and illuminate the principle ofeach procedure.Several applications are demonstrated in Section 4 to show the effectiveness of our decomposition.Section 5 concludes this paper.

2 Background

The goal of edge-preserving decomposition is to remove the high-frequency details from an input image,while keeping both the transitions and profiles of edges.We show a 1D signal in Fig.1 to provide intuition.The local signal is decomposed into three main components:a high-frequency detail signal,a step edge,and a slowly-varying shape signal.The detail signal represents the texture element with approximate zero mean.The edge signal depicts the margin of a visually salient segment.The shape signal contains the overall shape of the local signal.To properly capture details,it is essential for the base layer to combine the edge signal with the shape signal,without being confused by details.Confusing the base layer with the detail layer results in unexpected artifacts or distortions[14]. 2.1 Energy minimization framework

Fig.1 A 1D signal consists of three optional components: a detail signal,an edge signal,and a shape signal.The edge component and the shape component(in the blue rectangle) combine to give the final output(in the green rectangle).

A wealth of image decomposition techniques have been advocated to compute the base layer.Some approaches[14,18,20]follow the same optimization framework based on a data term and a smoothness term.The goal of the data term is to decrease the distance between the filtered image and the original one,while the smoothness term endeavors to achieve flatness in textured regions.Formally, given an input image I,seeking a smoothed image S can be expressed as solving the energy minimization problem:

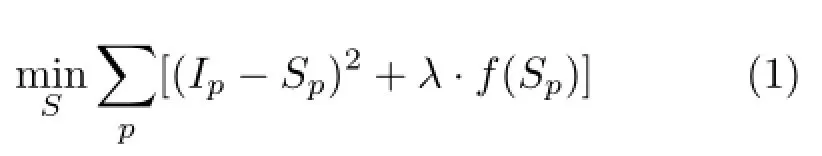
where the subscript p denotes the spatial location of a pixel.The function f(·)is carefully designed to control the smoothness of each pixel in the output image.Balancing the two possibly contradictory terms,the data term(Ip−Sp)2and the smoothness term f(Sp),enables us to compute the coarsened image S.Here,λ balances the two terms;a larger value leads to a smoother outcome.

2.2 Edge-preserving image smoothing

Edge-preserving image smoothing has already received a great deal of attention.Historically,a Gaussian filter is the most commonly used linear scale-space smoothing operator.Nonlinear scalespaceoperatorsimproveupon linearoperators by integrating a priori edge information into the smoothing process.In particular,the bilateral filter[11]and its extensions[2,4,21,22]are popular choices which have been applied in various multiscale decomposition scenarios[23,24].

Weighted least squares.Farbman et al.[14] advanced an edge-preserving operator based on the weighted least squares(WLS)framework,which correlates the smoothness function f in Eq.(1) with the gradients of S.Figure 2(b)illustrates theperformanceofWLS filtering.There are several inevitable limitations since the smoothing coefficients locate edges using large amplitudes.WLS filtering not only fails to smooth fine-scale highcontrast details,but also gets confused when edges touch details.We can increase the value of λ to provide smoother output(see Fig.2(c)).However,it produces deformations where the shape component is not flat(see the leftmost part of the plot of the signal,for example),and some edges become degraded. Such undesirable outcomes result from the naive design of the smoothness weights.

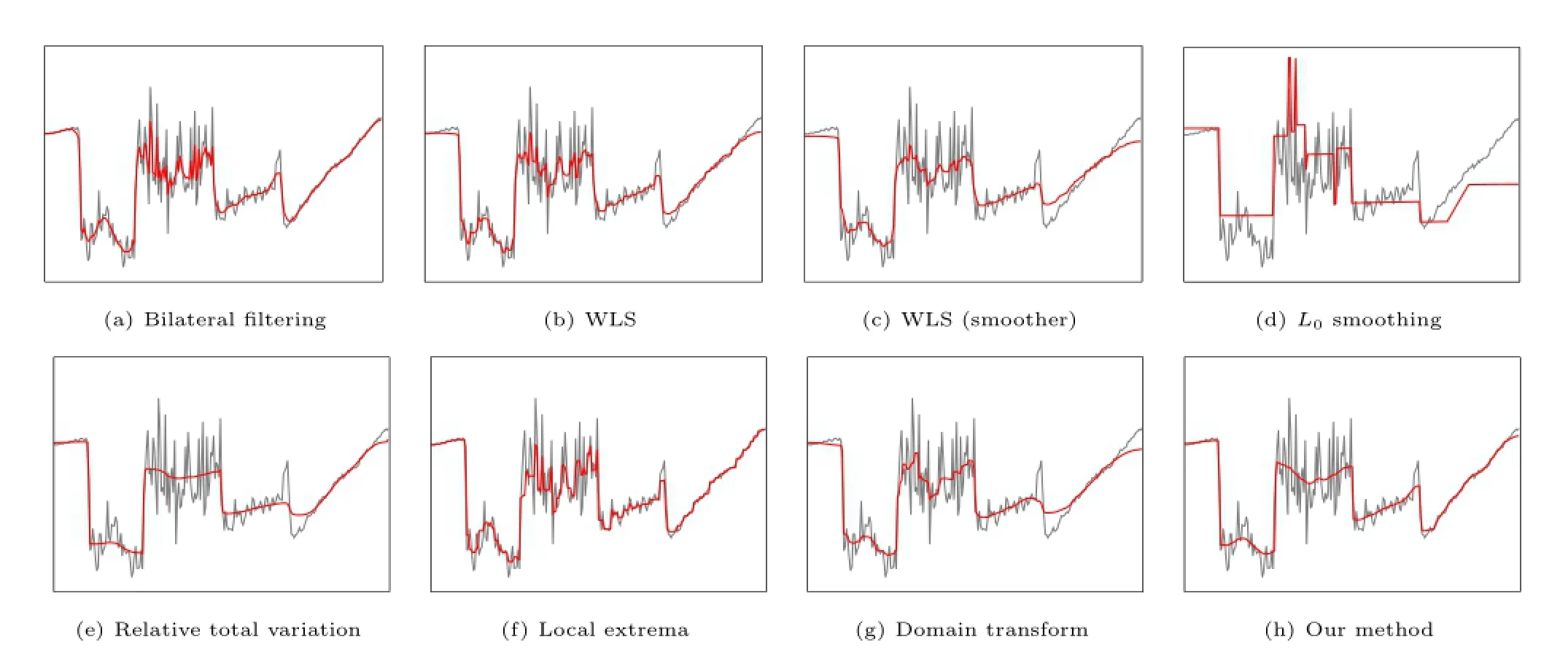
Fig.2 The gray curve represents a scanline of an input image;the red curve is the smoothed result.(a)Bilateral filtering[11] (σs=4,σr=0.2);(b)weighted least squares optimization(λ=0.5,α=1.2);(c)weighted least squares optimization(λ=1.5, α=1.2);(d)L0smoothing(λ=2e−2,κ=2.0);(e)relative total variation(λ=1e−2,σ=3.0);(f)local extrema[17];(g)domain transform[19](σs=20,σr=0.4);and(h)our method(λ1=0.4,λ2=3e−2,λ3=4e−3,α=2.2).

L0smoothing. Xu et al.[20]used a sparse gradient counting scheme to enhance the steepness of transition and eliminate a certain amount of lowamplitude structures.The smoothness function f is defined in a global manner by limiting the number of non-zero gradients.An alternative approach to optimization is used,since the original problem involves a discrete counting metric.However,this solverconserves the largestgradients in each iteration instead of intensities,which consequently gives rise to several drawbacks(see Fig.2(d)).Highcontrast textures are sharpened,while low-contrast edges are flattened.Some details may be overly smoothed,since the smallest gradients need to be set to zero.

2.3 Structure-texture image decomposition Structure-texture decomposition[25,26],focusing on the separation of structure components and texture components,traditionally enforces the total variation(TV)regularizer to preserve large-scale edges[27-30].Aujol et al.[27]studied different TV energy terms and functional spaces that suit various types of textures.These forms of total variation regularizer have limited abilities,since textures are usually complex and irregular.

Fig.3 Our pipeline involves three successive stages(labeled in green): detailsuppression,edgeextraction,and shape recovery.The resultofeach stage isshown in a blue rectangle.Taking the WLS optimization framework as a bridge, weimposeshapeconstraints(from theinputimage)and smoothness constraints(from the edge-guided image)on the output image to achieve base-detail decomposition.

Relative total variation.Xu et al.[18]proposed the relative total variation(RTV)regularizer for the smoothness function f.This measure yields different responses to meaningful content and texture edges, which assists in texture removal.Figure 2(e)shows the success of RTV in making the main structure stand out.However,it cannot distinguish between edges and textures that are close in scale,since they may be penalized similarly with respect to the regularizer.

3 Our approach

In this section,we explain our method using the joint weighted least squares framework.At the outset it generates a reference image containing structure information.This reference image helps to reduce the gap between the output base layer and the original appearance.We now explain the principles behind,and relationships of,the three main steps.

3.1 Overview

The pipeline of our approach,diagramed in Fig.3, includes three major procedures(indicated by green arrows):detail suppression,edge extraction,and shape recovery.Given an input image,we first compress details or textures to guarantee that their amplitudes are smaller than those of edges.Next,we can detect salient edges using existing methods,since the amplitudes of details have been reduced.The consequentexcessivesmoothing,which willbe elaborated later,does not matter,because we just require a guide image to reflect the structure.This edge-guided imagethen suppliesasmoothness constraint,while the input image supplies a shape constraint(indicated by orange arrows).Ultimately, using the WLS optimization framework as a bridge, we produce the final smoothed image which matches the overall shape of the input image elements.

3.2 Detail suppression

We define a windowed variation similarity measure at a pixel p in an image I to be

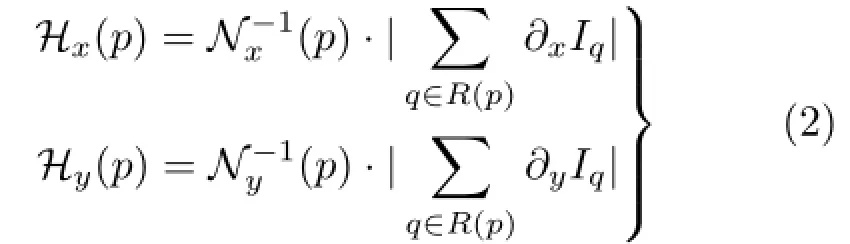
whereR(p)isthesetofpixelsin thelocal neighborhood centered at p,and∂xIqand∂yIqdenote the partial derivatives of I along the x and y directions respectively.Each direction is normalized via

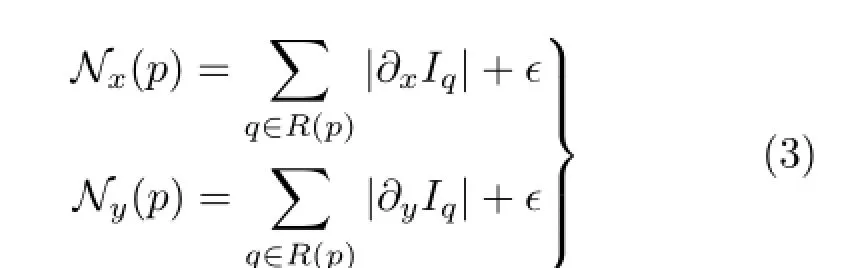
We set∈to a small positive number to avoid division by zero;Hxand Hyboth range from 0(when the derivatives in the local neighborhood R sum to zero) to 1(when the derivatives in the local neighborhood R coincide in sign).

A key observation isthatthe gradientsof details widely vary in direction in a small area while those of edges usually conform in terms of direction.Therefore,the quantity of H,which represents the intensity differences within R,is relatively smaller in detail regions.Our windowed variation similarity measure is inspired by Xu et al.[18].However,the largest distinction lies in the removal of the weights for neighboring pixels in their relative total variation measure.Our work reveals that weights are insignificant because all the pixels contribute equally when calculating the gradient variation in a local region.

Farbman et al.[14]suggested setting the smoothness function f in Eq.(1)to

We achieve detail suppression by incorporating the windowed variation similarity into the coefficient a(Ip)as

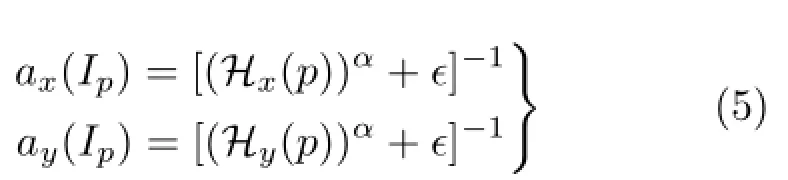
where α is a positive number which controls the sensitivitytoH.Notethatawindow merely containing textures has a larger value of a to enforce smoothness,while a window including structural edges imposes a milder smoothness requirement.

A closed-form solver for the WLS framework was provided in Ref.[14].We give the pseudocode of their scheme in Algorithm 1.Substituting our new weights(in Eq.(5))provides the intuitive output in Fig.4(b),which successfully suppresses the highcontrast details without degrading edges.

Algorithm 1:Weighted least squares(WLS) Input:An input image I,smoothing parameter λ,and smoothness weights axand ay. Output:A smoothed base layer S. Steps: 1)Ax←diagonal matrix containing ax; 2)Ay←diagonal matrix containing ay; 3)Dx←discrete differentiation operator along the x direction; 4)Dy←discrete differentiation operator along the y direction; 5)L←DTxAxDx+DTyAyDy; 6)E←identity matrix; 7)S←(E+λL)−1I.

3.3 Edge extraction

Recently,Xu et al.[20]proposed an L0gradient minimization strategy by limiting the number of pixels p whose magnitude is not zero.The gradient measure of an image S is written as

Fig.4 The three steps of our algorithm.(a)A scanline of intensity along a row in a real image.(b)Step 1:suppress high-contrast details using the windowed variation similarity measure;outcome shown in green.(c)Step 2:extract the salient structure layer (blue)from the image with low-contrast detail(green).(d)Step 3:fit the original shapes according to the edge-guided image(blue) and the input image;final output shown in red.

where#{·}is the counting operator.Used as the smoothness function f in Eq.(1),the gradient measure provides the objective function:

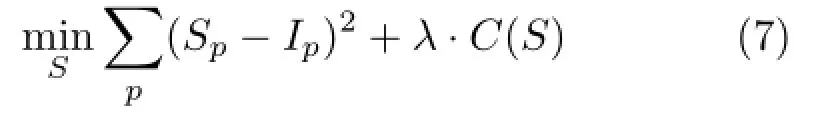
There isa crucialaspectofL0smoothing relevant to our edge extraction stage design-it picks out major edges and eliminates insignificant details.Therefore,it is a feasible tool to distinguish structure constituents now that the amplitudes of details have dropped below those of edges.We apply L0smoothing to the detail-suppressed image produced in the previous stage to give an edge-guided image for the final shape recovery phrase.

An inevitable side-effect of the L0operation is the severe intensity offset,as shown in Fig.4(c).This hinders succeeding delicate operations.However,it does not matter,as the generated edge-guided image includes the essential information which discerns edges from details.We explain the information as the possibility of a pixel belonging to an edge.Some non-edge regions are treated as constant(implying zero gradient)and hence have zero probability of containing a structural edge.The large-amplitude edges,even though compressed,still have larger gradients than the small-amplitude edges,and hence a greater chance of being an edge.

3.4 Shape recovery

We rectify the offset and oversmoothing problem utilizing joint weighted least squares,an extension of the WLS strategy[14].In our implementation, weimporttheedge-guided imageasa joint image for the ultimate purpose of detail-smoothing, edge-preserving,and shape-fitting.The smoothness function f is defined as in Eq.(4).However, the coefficients in this stage depend on the joint image J:

where the exponent β determines the sensitivity to the gradients of J.The probability information in J, together with I,controls the gradients of the output image.Combining the characteristics of the WLS framework and the knowledge from the edge-guided image,we recover the initial appearance,meeting our original goals.

Solving the energy minimization framework by Algorithm 1 with new weights produces a final coarsened base layer in Fig.4(d),with smoothed high-contrast details excluding edges,yet which still follows the overall signal form.

3.5 Results

To complete the exposition of our joint weighted least squares strategy,we summarize it in Algorithm 2, which affords a coarse base layer.Iterative smoothing operations on the returned base layer by Algorithm2 can provide a multiscale decomposition of an input image,which can be a more satisfactory result.However,we do not explore this further in this paper.

Algorithm 2:Joint weighted least squares Input:An input image I,smoothing parameters λ1, λ2,and λ3for the three stages,and sensitivity parameters α and β. Output:A smoothed base layer S. //Detail suppression 1)for all p∈I do 2) Solve Eq.(5)for ax(Ip)and ay(Ip); 3)end for 4)G←WLS(I,λ1,ax(I),ay(I)); //Edge extraction 5)J←L0smoothing(G,λ2); //Shape recovery 6)for all p∈J do 7) Solve Eq.(8)for ax(Jp)and ay(Jp); 8)end for 9)S←WLS(I,λ3,ax(J),ay(J)).

We compare our method with several others which perform base-detail decomposition.One should keep in mind that our goal is to seek a smoothed base layer in an edge-preserving and shape-fitting manner.All the parameters were carefully adjusted to achieve the best performance for these methods.Figure 5(a) shows some heart-shaped cookies with decorations on the surface.It is apparent that Figs.5(b)-5(f) exhibit poor outcomes.Some treat textures as edges and therefore preserve or sharpen them instead of smoothing them,while others blur strong edges in the coarsening process.Relative total variation (in Fig.5(g))produces subtle,yet visible,residual details on the surface of the back cookie.Our method (see Fig.5(h))performs best,with excellent removal of details without affecting edges and the entire shape.

Figure 6 exemplifies another comparison on the well-known“Barbara”image.We decompose the input image(Fig.6(a))into a smoothed base layer(Fig.6(b)))and a detail layer(Fig.6(c)).A representative signal indicated by the yellow line is taken to illustrate the traits of our algorithm (see Fig.6(d)).Despite the large amplitude of some oscillations,a piecewise smooth base signal is still extracted,plus a detail signal oscillating near a zero value.We combine the original signal and the coarsened base signal to demonstrate the accurate capture of the initial appearance.Other existing approaches in Figs.6(e)-6(h)cause severe sideeffects,with results far from satisfactory.

4 Applications

Our approach can be used as the basis of numerous image editing and manipulation tasks due to its fundamental properties of detail suppression,edge preservation,and shape matching.We demonstrate the abilities of the joint weighted least squares framework via several practical applications.

4.1 Detail enhancement

Detail enhancement is the process of representing detail in an amplified manner.Given an input image in Fig.7(a),we simply double the intensity of the detail layer to achieve the detail magnification result,without artifacts or blurring,in Fig.7(d).We highlightthe significance ofthe correctdetail determination that is embedded in the property of shape fitting.To provide understanding,a scanline signal(indicated by the yellow line)is plotted in the bottom row.The detail-enhanced signal(in red)is supposed to vibrate about,rather than deviate from, the initial one(in gray).

Fig.5 Results and comparison on an image with high-contrast details.

Fig.7 Detail boosting results.Top:input image and its detail enhanced output using various methods.Bottom:corresponding intensity plots indicated by the yellow line.

The results of the L0smoothing and the weighted least squares operator,taken directly from Ref.[20] and Ref.[14]respectively,both fail to fit the original shape.Our decomposition which provides appropriate enhancement and a more sophisticated boosting mechanism,instead of simply doubling, could be used to provide a more advanced outcome.

4.2 Image abstraction

Textures and details enrich the visual perception of a photo.However,in some situations,we prefer simplified stylistic pictures from color images or videos.This non-photorealistic processing technique demands elimination of details without degrading edges.Traditionally,bilateral filtering is widely used in image and video abstraction[23,24].Using our edge-preserving decomposition approach produces the results in Fig.8.In this application,we simultaneously suppressdetailsand emphasize edges.Two main steps are involved-extracting the smooth base layer,and detecting the edge component.We discern edges according to the gradient map of the base layer,following which the intensity of these edges is enhanced.The coarsened image is then overlaid with the enhanced edgesto augment the visual distinctiveness of different regions.

Fig.8 Image abstractions computed using our framework.

4.3 HDR tone mapping

HDR tone mapping is another popular application that aims to approximate the appearance of high dynamic range images in a medium that has a more limited dynamic range.The focus lies in maintaining detail contrast and compressing edge range.This goal can be achieved by harnessing image decomposition techniques[4,33,34].We use the tone mapping algorithm of Ref.[4]by simply replacing the bilateralfiltering with our decomposition algorithm.The base layer is linearly mapped to a low dynamic range and then composed back with the detail layer.It is of prime importance to carefully preserve sharp discontinuities to avoid halos.

Figure 9 shows results using several different methods.Structures can be clearly recognized and contrasts are reasonably maintained.Another instance is given in Fig.10.The comparison of two close-ups in the bottom row reveals that our method can generatestrongercontrastswithoutvisual artifacts such as blocky reflections(in Fig.10(a)and Fig.10(b))on the floor.

5 Conclusions

The ability to perform edge-preserving image decomposition opens up a wide range of possibilities for interesting photographic applications.We have presented a feasible optimization framework via joint weighted least squares to compute a coarsened base layer with the properties of detail smoothing, edge preservation,and shape fitting.We endeavor to impose shape constraints and smoothness constraints on the output image to address certain shortcomings of previous approaches.Our results for a variety ofapplications, involving detail enhancement,HDR tonemapping,andimage abstraction,demonstrate that our strategy is robust and versatile.

Our future work will concentrate on improving the performance under more complicated lighting and reducing the sensitivity to parameters.Another direction for future work is to explore further potential applications based on challenging image manipulations.

Acknowledgements

This work was sponsored by the National Basic Research Program of China(No.2011CB302203), the National Natural Science Foundation of China (Nos.61133009 and 61472245),and the Science and Technology Commission of Shanghai Municipality Program(No.13511505000).All the images used came from the homepages of previous projectsdirected by other authors.We would like to thank all the photographers who shot these photos.

Fig.9 HDR tone mapping results of the“small office”image.

Fig.10 Top:HDR tone mapping results and comparison on the“memorial”image.Bottom:corresponding close-ups.

Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use,distribution,and reproduction in any medium,provided the original author(s)and the source are credited.

[1]Eisemann, E.; Durand, F.Flash photography enhancement via intrinsic relighting. ACM Transactions on GraphicsVol.23,No.3,673-678,2004.

[2]Petschnigg,G.;Szeliski,R.;Agrawala,M.;Cohen, M.;Hoppe,H.;Toyama,K.Digital photography with flash and no-flash image pairs.ACM Transactions on Graphics Vol.23,No.3,664-672,2004.

[3]Bae, S.; Paris, S.; Durand, F. Two-scale tonemanagementforphotographic look.ACM Transactions on Graphics Vol.25,No.3,637-645, 2006.

[4]Durand,F.;Dorsey,J.Fast bilateral filtering for thedisplayofhigh-dynamic-rangeimages.ACM Transactions on Graphics Vol.21,No.3,257-266, 2002.

[5]Khan,E.A.;Reinhard,E.;Fleming,R.W.; B¨ulthoff,H.H.Image-based material editing.ACM Transactions on Graphics Vol.25,No.3,654-663, 2006.

[6]Huang,S.-S.;Zhang,G.-X.;Lai,Y.-K.;Kopf, J.;Cohen-Or,D.;Hu,S.-M.Parametric meta-filter modeling from a single example pair.The Visual Computer Vol.30,Nos.6-8,673-684,2014

[7]Burt,P.J.;Adelson,E.H.The Laplacian pyramid as a compact image code.IEEE Transactions on Communications Vol.31,No.4,532-540,1983.

[8]Black,M.J.;Sapiro,G.;Marimont,D.H.;Heeger, D.Robust anisotropic diffusion.IEEE Transactions on Image Processing Vol.7,No.3,421-432,1998.

[9]Lagendijk,R.L.;Biemond,J.;Boekee,D.E. Regularized iterative image restoration with ringing reduction.IEEE Transactions on Acoustics,Speech and Signal Processing Vol.36,No.12,1874-1888, 1988.

[10]Perona,P.;Malik,J.Scale-space and edge detection using anisotropic diffusion.IEEE Transactions on Pattern Analysis and Machine Intelligence Vol.12,No. 7,629-639,1990.

[11]Tomasi,C.;Manduchi,R.Bilateral filtering for gray and color images.In:Sixth International Conference on Computer Vision,839-846,1998.

[12]Bhat,P.;Zitnick,C.L.; Cohen,M.;Curless, B.GradientShop:A gradient-domain optimization framework forimageand videofiltering.ACM Transactions on Graphics Vol.29,No.2,Article No. 10,2010.

[13]Cheng,X.;Zeng,M.;Liu,X.Feature-preserving filtering with L0gradient minimization.Computers& Graphics Vol.38,150-157,2014.

[14]Farbman,Z.;Fattal,R.;Lischinski,D.;Szeliski, R.Edge-preserving decompositions for multi-scale tone and detail manipulation.ACM Transactions on Graphics Vol.27,No.3,Article No.67,2008.

[15]Paris,S.;Hasinoff,S.W.;Kautz,J.Local Laplacian filters:Edge-aware image processing with a Laplacian pyramid.ACM Transactions on Graphics Vol.30,No. 4,Article No.68,2011.

[16]Li,X.-Y.;Gu,Y.;Hu,S.-M.;Martin,R.R. Mixed-domain edge-aware image manipulation.IEEE Transactions on Image Processing Vol.22,No.5, 1915-1925,2013.

[17]Subr,K.;Soler,C.;Durand,F.Edge-preserving multiscale image decomposition based on local extrema.ACM Transactions on Graphics Vol.28,No. 5,Article No.147,2009.

[18]Xu,L.; Yan,Q.; Xia,Y.; Jia,J.Structure extraction from texture via relative total variation. ACM Transactions on Graphics Vol.31,No.6,Article No.139,2012.

[19]Gastal,E.S.L.;Oliveira,M.M.Domain transform for edge-aware image and video processing.ACM Transactions on Graphics Vol.30,No.4,Article No. 69,2011.

[20]Xu,L.;Lu,C.;Xu,Y.;Jia,J.Image smoothing via L0gradient minimization.ACM Transactions on Graphics Vol.30,No.6,Article No.174,2011.

[21]Choudhury,P.;Tumblin,J.The trilateral filter for high contrast images and meshes.In: ACM SIGGRAPH 2005 Courses,Article No.5,2005

[22]Su,Z.;Luo,X.;Deng,Z.;Liang,Y.;Ji,Z.Edgepreserving texture suppression filter based on joint filtering schemes.IEEE Transactions on Multimedia Vol.15,No.3,535-548,2013.

[23]Chen,J.;Paris,S.and;Durand,F.Real-time edgeaware image processing with the bilateral grid.ACM Transactions on Graphics Vol.26,No.3,Article No. 103,2007.

[24]Winnem¨oller,H.;Olsen,S.C.;Gooch,B.Real-time video abstraction.ACM Transactions on Graphics Vol.25,No.3,1221-1226,2006.

[25]Karacan,L.;Erdem,E.;Erdem,A.Structurepreserving image smoothing via region covariances. ACM Transactions on Graphics Vol.32,No.6,Article No.176,2013.

[26]Su,Z.; Luo,X.; Artusi,A.A novelimage decomposition approach and its applications.The Visual Computer Vol.29,No.10,1011-1023,2013.

[27]Aujol,J.-F.;Gilboa,G.;Chan,T.;Osher,S. Structure-texture image decomposition—modeling, algorithms,and parameter selection.International Journal of Computer Vision Vol.67,No.1,111-136, 2006.

[28]Meyer,Y.Oscillating Patterns in Image Processing and Nonlinear Evolution Equations:The Fifteenth Dean Jacqueline B.Lewis Memorial Lectures.Boston, MA,USA:American Mathematical Society,2001.

[29]Rudin,L.I.;Osher,S.;Fatemi,E.Nonlinear total variation based noise removal algorithms.Physica D: Nonlinear Phenomena Vol.60,Nos.1-4,259-268, 1992.

[30]Yin,W.;Goldfarb,D.;Osher,S.Image cartoontexture decomposition and feature selection using the total variation regularized L1functional.In: Proceedings of the Third international conference on Variational,Geometric,and Level Set Methods in Computer Vision,73-84,2005.

[31]Zhang,Q.;Shen,X.;Xu,L.;Jia,J.Rolling guidance filter.In:Computer Vision-ECCV 2014. Lecture Notes in Computer Science Volume 8691. Fleet,D.;Pajdla,T.;Schiele,B.;Tuytelaars,T.Eds. Switzerland:Springer International Publishing,815-830,2014.

[32]He,K.;Sun,J.;Tang,X.Guided image filtering. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol.35,No.6,1397-1409,2013.

[33]Li,Y.;Sharan,L.;Adelson,E.H.Compressing and companding high dynamic range images with subband architectures.ACM Transactions on Graphics Vol.24, No.3,836-844,2005.

[34]Tumblin,J.;Turk,G.LCIS:A boundary hierarchy for detail-preserving contrast reduction.In:Proceedings of the 26th annual conference on Computer graphics and interactive techniques,83-90,1999.

Pan Shao received the B.S.degree in computer science from Shanghai Jiao Tong University in 2013.She is now workingtoward theM.S.degreein the Department of Computer Science and Engineering at Shanghai Jiao Tong University.Her research interests lie in image editing and face recognition.

Shouhong Ding received the B.S.and M.S. degrees from the School of Mathematical Sciences in Dalian University of Technology, China, in 2008 and 2011,respectively.He isnow a Ph.D.candidate in the Department of Computer Science and Engineering,Shanghai Jiao Tong University,China.His current research interests include image/video editing,computer vision,computer graphics, and digital media technology.

Lizhuang Ma received his Ph.D.degree from Zhejiang University in 1991.He is now a full professor, Ph.D.tutor,and thehead ofthe Digital Media Technology and Data Reconstruction Lab at the Department of Computer Science and Engineering, Shanghai Jiao Tong University since 2002.He is also the chairman of the Center of Information Science and Technology for Traditional Chinese Medicine in Shanghai Traditional Chinese Medicine University.His research interests include computer-aided geometric design, computer graphics,scientific data visualization,computer animation,digital media technology,and theory and applications for computer graphics,CAD/CAM.

Yunsheng Wu received his B.S.degree in computer science from Peking University,China.He is now a product director in Tencent Inc.,China.He is responsible for QQ video,Pitu,QQ tornado,and Watermark Camera.His current research interest is face recognition.

Yongjian Wu received the M.S.degree from ComputerSchoolin Wuhan University, China, in 2008.He is now aseniorresearcherin Tencent Inc., China. His current research interests include computer vision, pattern recognition,and digital media technology.

1Department of Computer Science and Engineering, ShanghaiJiao Tong University, Shanghai200240, China.E-mail:pshao@sjtu.edu.cn,dingsh1987@gmail. com,ma-lz@cs.sjtu.edu.cn().

2Tencent Inc.,China.

Manuscript received:2014-11-15;accepted:2015-02-02