Least-squares images for edge-preserving smoothing

Hui Wang,Junjie Cao,Xiuping Liu(),Jianmin Wang,Tongrang Fan,and Jianping Hu

©The Author(s)2015.This article is published with open access at Springerlink.com

Least-squares images for edge-preserving smoothing

Hui Wang1,Junjie Cao2,Xiuping Liu2(),Jianmin Wang1,Tongrang Fan1,and Jianping Hu3

©The Author(s)2015.This article is published with open access at Springerlink.com

In this paper,we propose least-squares images(LS-images)as a basis for a novel edgepreserving image smoothing method.The LS-image requires the value of each pixel to be a convex linear combination of its neighbors,i.e.,to have zero Laplacian,and to approximatethe original image in a least-squares sense.The edge-preserving property inherits from the edge-aware weights for constructing the linear combination.Experimental results demonstrate that the proposed method achieves high quality results compared to previous state-of-theart works.We also show diverse applications of LS-images,such as detail manipulation,edge enhancement, and clip-art JPEG artifact removal.

feature-preserving;image enhancement; image smoothing;least-squares images (LS-images)

1 Introduction

Edge-preserving image smoothing hasemerged as a valuable toolfor many applications in image processing and computer graphics,and has received much attention[1-12].However,it is still a challenging problem due to the difficulty of distinguishing sharp edges from noises.

Ofthepreviousmethodsforedge-preserving image smoothing, some are gradient domain methods,which generally specify both zerothorder constraints to provide desired pixel valuesand first-order differential constraints to provide desired pixel gradients,examples being the total variation model[2],WLS optimization[5],and L0smoothing[9,12].Inspired by use of secondorder differential Laplacian constraints for image colorization[13]and segmentation[14],we propose least-squares images(LS-images)as a basis for a novel edge-preserving image smoothing method. The LS-image is constructed with inhomogeneous Laplacian constraints set to zero and approximates the original image in a least-squares sense.The edgepreserving property is achieved by using edge-aware weights to compute the inhomogeneous Laplacian. Minimizing second-order Laplacians with vertex constraints has been widely used in digital geometry processing,for purposes such as smoothing[15, 16],geometry compression [17],and high-pass quantization[18].

Experimental results demonstrate the proposed method achieves high quality results.The LS-image is simple,robust,and versatile,and may be used in many of the applications that have so far been based on previous approaches.It can be used for detail manipulation,edge enhancement,and clip-art compression artifact removal.

The rest of this paper is organized as follows. Section 2 describes previous work on edgepreserving imagesmoothing.TheLS-imageis introduced in Section 3.Experimental results and comparisons with existing methods are discussed in Section 4.Applications of LS-images are demonstrated in Section 5.Finally this paper is concluded in Section 6.

2 Previous work

Edge-preserving image smoothing,which smooths small details and preserves sharp edges,has already received a great deal of attention.A full reviewof edge-preserving image smoothing is beyond the scope of this paper.In this section,only approaches that are most relevant to the proposed one are surveyed.

2.1 Explicit weighted-average methods

Classicalbilateralfiltering [3]is perhaps the simplest and most intuitive of the explicit weightedaverage methods.It smooths each pixel as a linear combination of its neighbors,where weights consider both spatial distance and range similarity.A number of efficient implementations of bilateral filtering have been proposed[19-21].A bilateral texture filter has also been proposed to effectively remove textures while preserving structures[22].Mean shift filtering[4]can also be regarded as an explicit weighted-average method,where a moving window is used to compute the average.Edge-avoiding wavelets with explicit image-adaptive weights can also be used for edge-preserving image smoothing[7]. However,constraints on kernel size of the wavelet may limit its applicability. Derived from a local linear model between a guidance image and the final filtering result,explicit and efficient guided filtering has been used for edge-preserving image smoothing[11].Another class of explicit edgepreserving filtering uses weights based on geodesic distances between pixels[23,24].Karacan et al.[25] proposed an explicitstructure-preserving image smoothing method,where the weights are derived from region covariances.Learning an image filter from a pair of example images is considered in Ref.[26].

As stated in Ref.[11],the local explicit weightedaverage methods have one limitation:unavoidable halosappearnearcertain weak edges.Global implicit methods attenuate these halos,at the price of high computational cost.Our proposed edgepreserving image smoothing method is a global implicit approach.

2.2 Gradient based methods

As a first-order differential quantity,the gradient contains information about details,and has been widely used in edge-preserving image smoothing[1, 5,9,12].Anisotropic diffusion achievesedgepreserving smoothing by use of an edge-stopping function to permit smoothing only in the interior of regions without crossing sharp edges;the edgestopping function is based on magnitudes of the gradients[1].The flexible weighted least-squares optimization framework achieves edge-preserving smoothing by minimizing gradients using edge-aware weights[5].Reconstructing images that minimize gradients in the L0norm is another state-of-theart edge-preserving smoothing approach[9,12].Xu et al.[27]proposed a new inherent variation and relative total variation measures,and developed an efficient optimization system to extract main structures from textures.

In this paper,the LS-image approach minimizes the Laplacian,which is a second-order differential quantity,to provide smoothing.The edge-preserving property of the LS-image is inherited from the edgeaware inhomogeneous Laplacian.

2.3 Other approaches

Paris et al.[10]manipulated the coefficients of the Laplacian pyramid around each pixel to provide edge-preserving smoothing.A mixed-domain edge-aware image manipulation method based on Gaussian pyramids was given in Ref.[28].Inspired by the 1D Hilbert-Huang transform(HHT),Subr et al.[6]proposed an edge-preserving image smoothing method based on averaging two envelops which fit the local maxima and minima of the image.An efficient structure-aware image smoothing method based local extrema on space-filling curves was proposed in Ref.[29].Edge-aware image smoothing methods have also been used for image and video abstraction[30,31].

3 Edge-preserving smoothing via LS-image

In this section,we first describe a novel edgepreserving smoothing method via the proposed LS-image,and then analysethemathematical relationship of our method to other related work. 3.1 LS-image

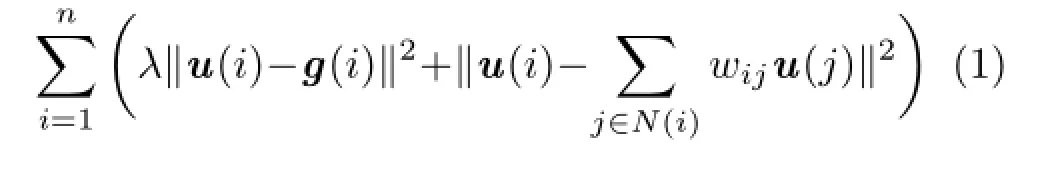
Given an original image g (gray or color)with n pixels,the LS-image u is an edge-preserving smoothing result,which minimizes the following energy:where i denotes the index of a pixel.The data term‖u(i)−g(i)‖2ensures the LS-image approximates theoriginalimage,whilethesmoothingterm constrains the value of each pixel to be a convex combination of the values of its neighbors N(i),so that each pixel has a zero Laplacian.As explained in Section 4.2,in this paper we fix N(i)to be the 3×3 neighborhood of pixel i.The parameter λ allows a trade-off between the data and smoothing terms; decreasing λ leads to a smoother LS-image u.

The non-linear weights wijplay an important role in the edge-preserving properties of LS-images.They are set as follows:

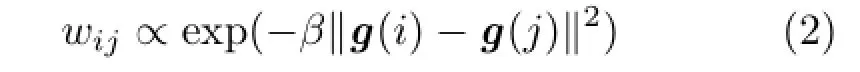
The energy in Eq.(1)can be uniquely minimized as the solution of the following linear system:

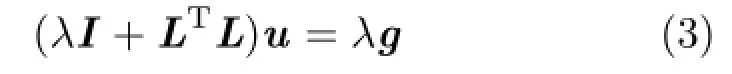
where I is the n-dimensional identity matrix,and L is an n×n inhomogeneous Laplacian matrix with elements

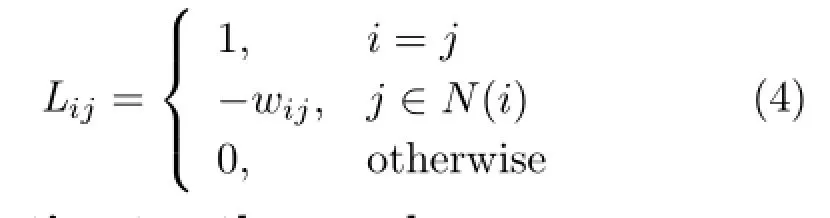
3.2 Relation to other work

Bilateral filter.As stated in Eq.(3),our edgepreserving LS-image may be expressed as applying the operator LSλ,β=λ(λI+LTL)−1to the original image vector g.Each row of LSλ,βcould be thought as a kernel that determines the value of the corresponding pixel as a weighted combination of other pixels in the original image.

In Fig.1,we compare our filter kernels with classical bilateral filters in Ref.[3].Firstly,it can be seen that filter kernels of the both two methods are edge-aware,and thus our smoothing method is spatially-variant filtering.Secondly,the support of filter kernels of our LS-image is much larger than the 3×3 neighbors in Eq.(1).

Fig.1 Filter kernels.Left:kernels are centered at the pixels denoted by the red dots.Middle:filter kernels for bilateral filtering with δs=5 and δr=0.1.Right:filter kernels for LS-images with β=100 and λ=10−5.

Weighted least-squares method.Both the LS-image and weighted least-squares(WLS)method in Ref.[5]can preserve sharp edges,by solving a linear system.The linear system for WLS is

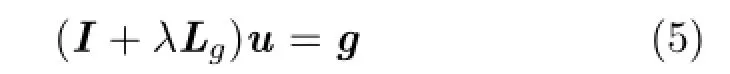
where Lgis a five-point spatially inhomogeneous Laplacian matrix,while the matrix L in Eq.(3) is an extended ten-point spatially inhomogeneous Laplacian matrix.

Thesmoothnessterm inWLSminimizesa first-orderdifferentialquantity, gradient, while the LS-image approach minimizes a second-order differentialquantity,theLaplacian.Theedgepreserving property ofWLS is achieved by minimizing homogeneous gradients with edge-aware weights,while LS-image uses edge-aware weights for computing the inhomogeneous Laplacian.In geometry processing,minimizingtheLaplacian correspondsto plateenergy,whileminimizing gradients corresponds to membrane energy[32].

We compare our LS-image with the WLS method in Fig.2,which demonstrates that our approach can generate clearer edges-see particularly the two cars in the top region.This is because WLS only considers the 4 nearest neighbors of a pixel in Eq.(5), while our LS-image approach takes into account the 25 nearest neighbors in Eq.(3).Thus,the interaction range τ,defined in Section 5 in Ref.[8],is τ=1 for WLS,while τ=2 for LS-images.

Image segmentation and colorization.The edge-aware smoothing term ofour LS-image approach in Eq.(1)is inspired by a colorization method based on optimization[13],and random walks for segmentation[14].However,these works use sparse and hard constraints,while in LS-images, all pixels are constrained in a soft linear squares sense for edge-preserving image smoothing.

Fig.2 Comparing our LS-image with the WLS result[5].

4 Implementation and results

In this section,we discuss implementation details, demonstrate that our method producing artifact-free results,and compare it to previous state-of-the-art approaches.

4.1 Implementation

Our algorithms were implemented in MATLAB on a PC with a 3.30 GHz Intel(R)core(TM)i3 CPU and 3.20 GB of RAM.They were not optimized for speed.The most time-consuming part of our method is solving the linear system in Eq.(3),using the builtin solver of MATLAB.It takes about 2s for the 384× 512 image in Fig.3.A C++implementation on a GPU would speed up our method.

4.2 Parameters

The LS-image approach has three parameters:choice of neighborhood N(i),λ to trade off smoothing and edge-preservation,and β for computing weights.

Figure 4 demonstrates the effects of choosing different neighborhoods N(i).It can be seen that enlarging N(i)gives better results,as observed in Ref.[8].However,a larger N(i)would destroy the sparse property of the inhomogeneous Laplacian matrix,and induce expensive computational cost.In this paper,we fixed N(i)to be the 3×3 neighbors of pixel i,following Refs.[6,13].

In Fig.3,LS-images with different values of λ are displayed.It can be seen that in all cases the sharp edges are preserved,while decreasing λ leadsto smoother images.In experiments,we find that λ=10−4or λ=10−6provides satisfactory results for most images.

Fig.3 LS-images for different values of λ(β is fixed at 3000).

Fig.4 The effect of using different neighborhoods N(i)for LS-images;β=1000 and λ=10−4are used from(b)to(c).

Figure 5 shows LS-images with different values of β,which controls the edge-preservation extent. Larger β preserves more sharp edges.If the variance of the grey of color is small,the parameter should also be small.For example,the variance of color in Fig.9 is small,so choosing a smaller β=100 would get desirable result.However,it is difficult to find a fixed or an automatic value for β for all images.

4.3 Comparisons with other methods

In this paper,we have carefully tuned the parameters used for all the methods compared,in order to generate the best results.

Guided filtering.We compare our method with the explicit guided image filtering method[11]in Fig.6,which demonstrates that our method can preserve weaker edges in the sky region indicated by a box,while guided filtering cannot.As analysed in Ref.[11],smoothing of weaker edges is a limitation of explicit methods such as bilateral filtering and guided filtering.Our LS-image approach,being an implicit method,can preserve weaker edges to some extent at the price of more greater computational cost.

Weighted least-squares method.In Fig.2,we compare our LS-image with the WLS method[5]. Our results are better than those of WLS,especially within the red box indicated.However,the WLS method isfasterthan ourmethod.Thetime taken by WLS and our method is 0.8s and 2.5s respectively.

L0gradient minimization. In Fig. 7, wecompare ourLS-image with L0gradient minimization[9].Our result can preserve sharp edges better than theirs,as shown in the highlighted box.Meanwhile,our approach takes about 3s,which is much faster than the L0gradient minimization cost of about 78 s for the CUP version.

Local Laplacian filter.Figure 8 compares our LS-image approach with local Laplacian filters via a Laplacian pyramid,as in Ref.[10].Both methods can preserve sharp edges,but our result is globally brighter and closer to the original image than theirs, especially in the indicated region showing hair and hat.This is because the local Laplacian filters just modify the coefficients of the Laplacian pyramid to obtain the final result without a data term to ensure closeness to the original image.

Fig.5 LS-images with different values of the parameter β(λ is fixed at 10−4).

Fig.6 Comparing our method with the guided filtering[11].(a)Input image;(b)the guided filtering result(r=16,ε=0.12); and(c)our LS-image(β=1000,λ=10−4).

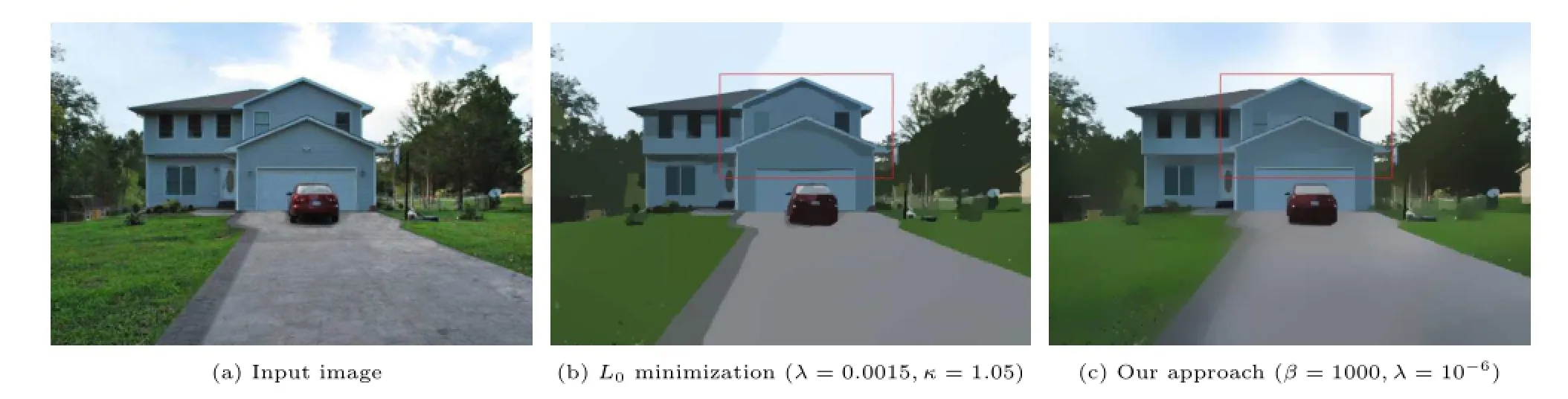
Fig.7 Comparing LS-images with L0gradient minimization((a)and(b)are directly reproduced from Ref.[9]).

Fig.8 The Lena image(left)smoothed using local Laplacian filters[10](middle)and our method with β=500 and λ=10−5(right).

Other previous work.In Fig.9,we compare our LS-image result with other classic previous edgepreserving smoothing methods:bilateral filtering[3], the mean-shift method [4],total variation [2], weighted least-squares optimization [5],and L0gradient minimization[9,12].It can be clearly shown that our method achieves comparable results to L0gradient minimization[12]for the step edge image, and generates better results than the other methods.

5 Applications

The proposed LS-image has many potential applications.We apply it to detail manipulation, edgeenhancement,and clip-artJPEG artifact removal.

5.1 Detail manipulation

An LS-image u can be seen as a smoothed base layer of the original image g in Eq.(3).Thus the original image can be decomposed as follows:

where d is the detail.Boosting the detail d can achieve detail manipulation.

Figure 10 shows that boosting using different smoothed layers can produce versatile detail manipulation effects.

Fig.9 (a)Image from Ref.[5],with added noise.Results using: (b)bilateral smoothing[3](δs=12,δr=0.5);(c)mean-shift smoothing[4](hs=10,hr=8);(d)total variation[2](λ=3); (e)weighted least-squares optimization[5](λ=2,α=3);(f) L0gradient minimization[9](λ=0.3,κ=2);(g)Cheng et al.’s method[12](λ=0.45);and(h)our method(β=100, λ=10−6).

Fig.10 Detail manipulation.(a)Input image;(b)and(c)two LS-images with different values of β(λ is fixed to 10−5);(d)and (e)enhanced results boosting detail,based on(b)and(c)respectively(2.0×).

5.2 Clip-art compression artifacts removal Currentimagecompression standards,suchas JPEG,when used with low bit rates lead to annoying visual artifacts,especially for cartoon images.LS-image processing is suitable for removing these artifacts,due to its edge-preserving property,as the approaches in Refs.[9,12](see Fig.11).

5.3 Edge enhancement

Some images like Fig.12(a)may contain tiny details making them indistinguishable from sharp edges. The output LS-image displayed in Fig.12(c),whose gradient map is shown in Fig.12(f),both removes small textures while preserving the main edges(see Fig.12(i)).The LS-image approach produces better results than the state-of-the-art work in Ref.[9].

6 Conclusions

In this paper,we define least-squares images(LS-images),which have zero inhomogeneous Laplacian and approximate the original image in a leastsquares sense,as a novel edge-preserving image smoothing approach.Comparisons with previous state-of-the-art edge-preserving image smoothing methodsdemonstrate itachieveshigh quality results.We have also shown that the LS-image approach can be applied to detail manipulation, edgeenhancement,and clip-artJPEG artifact removal.A limitation,however,is that the proposed smoothing method cannot extract main structures from complex textured patterns.

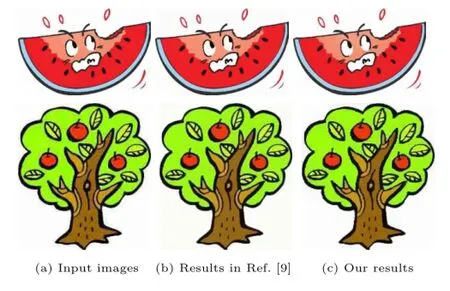
Fig.11 JPEG artifact removal. (a)Low quality JPEG compressed images. (b)Restoration results via L0gradient minimization.(c)Restoration via LS-images(β=1000,λ= 0.0001).

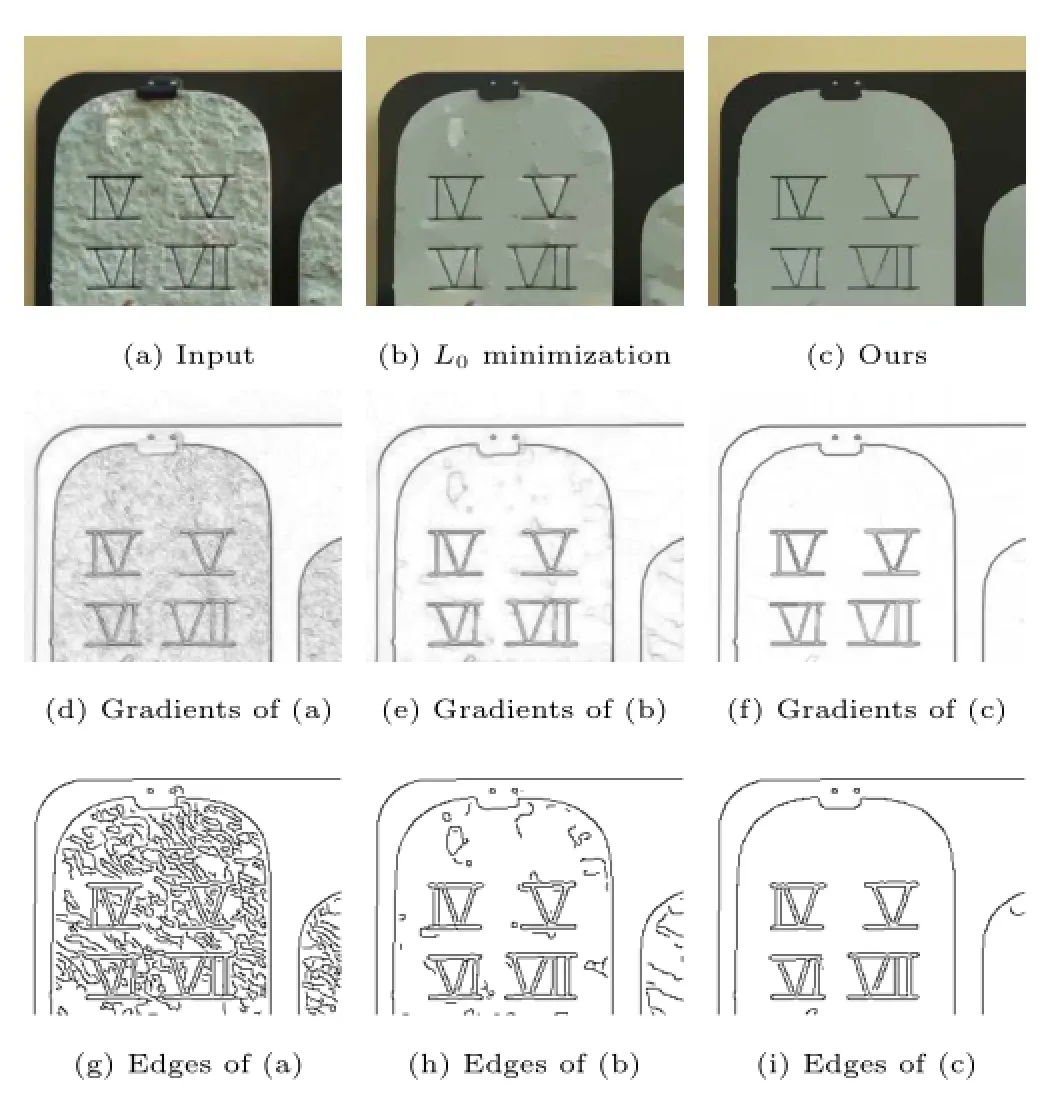
Fig.12 Smoothing for edge enhancement and detection.Our LS-image(c)(β=500,λ=10−8)suppresses low-amplitude details and enhances high contrast edges better than the method in Ref.[9](b)(figure directly copied from their paper).(d)-(f) are gradient maps of(a)-(c),scaled for visualization.(g)-(i)are Canny edges of(a)-(c).

For future work,we would like investigate further image smoothing methods that minimize other differential quantities,such as curvature.We will also seek further applications for our LS-images,and intend to extend our LS-images to extract structures from complex textures,as in Refs.[22,25,27].

Acknowledgements

We would like to thank the anonymous reviewers for their valuable comments.Most images in this paper come from other researchers and we thank them for making their data and code available.The results in Figs.9(b)-9(g)were shared by the authors ofRef.[12].This work is supported by National Natural Science Foundation ofChina (Nos.61402300, 61373160,61363048,61173102,61370143,and 61202261),Natural Science Foundation of Hebei Province(No.F2014210127),the Funded Projects for Introduction of Overseas Scholars of Hebei Province,Funds for Excellent Young Scholar of Shijiazhuang Tiedao University,and Scientific and Technological Development Plan of Jilin Province (No.20130522113JH).

Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use,distribution,and reproduction in any medium,provided the original author(s)and the source are credited.

[1]Perona,P.;Malik,J.Scale-space and edge detection using anisotropic diffusion.IEEE Transactions on Pattern Analysis and Machine Intelligence Vol.12,No. 7,629-639,1990.

[2]Rudin,L.I.;Osher,S.;Fatemi,E.Nonlinear total variation based noise removal algorithms.Physica D: Nonlinear Phenomena Vol.60,Nos.1-4,259-268, 1992.

[3]Tomasi,C.;Manduchi,R.Bilateral filtering for gray and color images.In:Sixth International Conference on Computer Vision,839-846,1998.

[4]Comaniciu,D.;Meer,P.Mean shift:A robust approach toward feature space analysis.IEEE Transactions on Pattern Analysis and Machine Intelligence Vol.24,No.5,603-619,2002.

[5]Farbman,Z.;Fattal,R.;Lischinski,D.;Szeliski, R.Edge-preserving decompositions for multi-scale tone and detail manipulation.ACM Transactions on Graphics Vol.27,No.3,Article No.67,2008.

[6]Subr,K.;Soler,C.;Durand,F.Edge-preserving multiscale image decomposition based on local extrema.ACM Transactions on Graphics Vol.28,No. 5,Article No.147,2009.

[7]Fattal, R. Edge-avoiding wavelets and their applications. ACM Transactions on Graphics Vol.28,No.3,Article No.22,2009.

[8]Farbman,Z.;Fattal,R.;Lischinski,D.Diffusion maps for edge-aware image editing.ACM Transactions on Graphics Vol.29,No.6,Article No.145,2010.

[9]Xu,L.;Lu,C.;Xu,Y.;Jia,J.Image smoothing via L0gradient minimization.ACM Transactions on Graphics Vol.30,No.6,Article No.174,2011.

[10]Paris,S.;Hasinoff,S.W.;Kautz,J.Local Laplacian filters:Edge-aware image processing with a Laplacian pyramid.ACM Transactions on Graphics Vol.30,No. 4,Article No.68,2011.

[11]He,K.;Sun,J.;Tang,X.Guided image filtering. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol.35,No.6,1397-1409,2013.

[12]Cheng,X.;Zeng,M.;Liu,X.Feature-preserving filtering with L0gradient minimization.Computers& Graphics Vol.38,150-157,2014.

[13]Levin,A.;Lischinski,D.;Weiss,Y.Colorization using optimization.ACM Transactions on Graphics Vol.23, No.3,689-694,2004.

[14]Grady,L.Random walks for image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence Vol.28,No.11,1768-1783,2006.

[15]Sorkine,O.;Cohen-Or,D.Least-squares meshes.In: Proceedings of the Shape Modeling International,191-199,2004.

[16]Sorkine,O.Differentialrepresentationsformesh processing.Computer Graphics Forum Vol.25,No.4, 789-807,2006.

[17]Sorkine,O.;Cohen-Or,D.;Irony,D.;Toledo,S. Geometry-aware bases for shape approximation.IEEE Transactions on Visualization and Computer Graphics Vol.11,No.2,171-180,2005.

[18]Chen,D.;Cohen-Or,D.;Sorkine,O.;Toledo,S. Algebraic analysis of high-pass quantization.ACM Transactions on Graphics Vol.24,No.4,1259-1282, 2005.

[19]Chen,J.;Paris,S.;Durand,F.Real-time edgeaware image processing with the bilateral grid.ACM Transactions on Graphics Vol.26,No.3,Article No. 103,2007.

[20]Yang,Q.;Tan,K.-H.;Ahuja,N.Real-time O(1) bilateral filtering.In:IEEE Conference on Computer Vision and Pattern Recognition,557-564,2009.

[21]Gastal, E.S.L.; Oliveira, M.M.Adaptive manifoldsforreal-timehigh-dimensionalfiltering. ACM Transactions on Graphics Vol.31,No.4,Article No.33,2012.

[22]Cho,H.;Lee,H.;Kang,H.;Lee,S.Bilateral texture filtering.ACM Transactions on Graphics Vol.33,No. 4,Article No.128,2014.

[23]Criminisi,A.;Sharp,T.;Rother,C.;P´erez,P. Geodesic image and video editing.ACM Transactions on Graphics Vol.29,No.5,Article No.134,2010.

[24]Gastal,E.S.L.;Oliveiral,M.M.Domain transform for edge-aware image and video processing.ACM Transactions on Graphics Vol.30,No.4,Article No. 69,2011.

[25]Karacan,L.;Erdem,E.;Erdem,A.Structurepreserving image smoothing via region covariances. ACM Transactions on Graphics Vol.32,No.6,Article No.176,2013.

[26]Huang,S.-S.;Zhang,G.-X.;Lai,Y.-K.;Kopf, J.;Cohen-Or,D.;Hu,S.-M.Parametric meta-filter modeling from a single example pair.The Visual Computer Vol.30,Nos.6-8,673-684,2014.

[27]Xu,L.; Yan,Q.; Xia,Y.; Jia,J.Structure extraction from texture via relative total variation. ACM Transactions on Graphics Vol.31,No.6,Article No.139,2012.

[28]Li,X.-Y.;Gu,Y.;Hu,S.-M.;Martin,R.R. Mixed-domain edge-aware image manipulation.IEEE Transactions on Image Processing Vol.22,No.5, 1915-1925,2013.

[29]Zang,Y.;Huang,H.;Zhang,L.Efficient structureaware image smoothing by local extrema on spacefilling curve.IEEE Transactions on Visualization and Computer Graphics Vol.20,No.9,1253-1265,2014.

[30]Zhang,S.-H.;Li,X.-Y.;Hu,S.-M.;Martin,R.R. Online video stream abstraction and stylization.IEEE Transactions on Multimedia Vol.13,No.6,1286-1294, 2011.

[31]Kyprianidis,J.E.;Kang,H.Imageand video abstraction by coherence-enhancing filtering. Computer Graphics Forum Vol.30,No.2,593-602,2011.

[32]Botsch, M.; Sorkine, O.On linearvariational surface deformation methods.IEEE Transactions on Visualization and Computer Graphics Vol.14,No.1, 213-230,2008.

Hui Wang is a lecturer in School of Information Science and Technology at Shijiazhuang Tiedao University,China. He received the Ph.D.degree in computational mathematics at Dalian University of Technology in 2013.His research interests include computer graphics,digital geometry processing, and image processing.

Junjie Cao is a lecturer in School ofMathematicalSciencesatDalian University of Technology, China. He received the Ph.D.degree in computational mathematics from Dalian University of Technology. Hisresearch interestsinclude shape modeling, image processing, and machine learning.

Xiuping Liu is a professor in School ofMathematicalSciencesatDalian University of Technology, China. She received the Ph.D.degree in computational mathematics from Dalian University of Technology. Her research interests include shape modeling and analysis.

Jianmin Wang is an associate professor in SchoolofInformation Science and Technology at Shijiazhuang Tiedao University,China.His current research interests include software engineering and network technology.

Tongrang Fan is a professor in School of Information Science and Technology at Shijiazhuang Tiedao University, China. Her current research interests includenetworktechnology,network security technology, and intelligent information processing.

Jianping Hu is an associate professor in College ofSciences at Northeast Dianli University,China.He obtained his B.S.and M.S.degrees in mathematics atJilin University. He received his Ph.D. degree in computational mathematics at Dalian University of Technology in 2009.His research interests include computer graphics,computational geometry,and image processing.

1School of Information Science and Technology, Shijiazhuang Tiedao University,Shijiazhuang 050043, China.

2School of Mathematical Sciences,Dalian University of Technology,Dalian 116024,China.E-mail:xpliu@ dlut.edu.cn().

3 School of Sciences,Northeast Dianli University,Jilin 132012,China.

Manuscript received:2014-09-26;accepted:2015-01-19