Poisson disk sampling through disk packing

Guanghui Liang,Lin Lu(),Zhonggui Chen,and Chenglei Yang

©The Author(s)2015.This article is published with open access at Springerlink.com

Poisson disk sampling through disk packing

Guanghui Liang1,Lin Lu1(),Zhonggui Chen2,and Chenglei Yang1

©The Author(s)2015.This article is published with open access at Springerlink.com

Poisson disk sampling is an important problem in computer graphics and has a wide variety of applications in imaging,geometry,rendering,etc.In this paper,we propose a novel Poisson disk sampling algorithm based on disk packing.The key idea uses the observation that a relatively dense disk packing layout naturally satisfies the Poisson disk distribution property that each point is no closer to the others than a specified minimum distance,i.e.,the Poisson disk radius.We use this property to propose a relaxation algorithm that achieves a good balance between the random and uniform properties needed for Poisson disk distributions.Our algorithm is easily adapted to image stippling by extending identical disk packing to unequal disks.Experimental results demonstrate the efficacy of our approaches.

disk packing;image stippling;Poisson disk sampling;power diagram

1 Introduction

Samplingisafundamentaltopicin computer graphics since it can be applied to many areas such as rendering and statistical study of shapes[1].The Poisson disk distribution,for instance,is one of the preferred graphical noise distributions,having blue noise-the samples are distributed in a both uniform and random manner.Due to its nice spatial and spectral properties,it is widely used in many applications such as halftoning and stippling[2,3],populating plants in virtual ecosystems[4],and geometry processing[5].

A Poisson disk distribution is a point set with the constraint that each point is separated from the others by a minimum distance 2r,where the parameter r is called the Poisson disk radius. The classical method for generating Poisson disk distributions is dart throwing[6],in which an iterative process randomly generates sample points in the domain and accepts them if they do not conflict with existing point.There is much follow-up work on the dart throwing algorithm.However,the results from this type of method could still be further optimized,to enlarge the disk size or to involve more samples,while retaining the blue noise properties.

In this paper,we take advantage of the essential connection between disk packing and the problem of Poisson disk sampling or image stippling,and use it to propose novel algorithms for improving the quality of existing Poisson disk distributions,and to generate image stippling based on the idea of disk packing. In the disk packing problem,the disks are arranged to maximise density subjected to the constraints that no overlap exists between any two disks.Based on the observation that this can be of benefit in Poisson disk sampling,we employ the disk packing algorithm to improve the quality of a given Poisson disk distribution,either by enlarging the Poisson disk radius,or by allowing more sample points while maintaining the same Poisson disk radius.As a result,we gain a better balance between the two properties of Poisson disk distributions.

Furthermore,we adapt the unequal disk packing problem to image stippling.

The main contributions of our paper are as follows:

·A novel method for improving the quality of given Poisson disk distributions,based on our disk packing algorithm.

·We adapt our method to image stippling,by generalizing the packing problem to unequal disks.

The remainder of this paper is organized as follows.Related work is briefly introduced in Section 2. Section 3 contains some preliminary ideas.In Sections 4 and 5,we present our Poisson disk sampling algorithm and image stippling algorithm respectively.Experiments and comparisons are made in Section 6 and we give conclusions in the last section.

2 Related work

In this section,we give a brief literature review of the topics most closely related to our work,namely Poisson disk sampling,disk packing,and image stippling.

2.1 Poisson disk sampling

During recent decades,many methods have been proposed to generate Poisson disk distributions. The classical algorithm is dart throwing[6];it can produce unbiased disk free point sets.During the dart throwing process,successive samples are thrown.Each is rejected if it is closer to the existing samples than the Poisson disk radius,otherwise it is accepted.Dart throwing is widely used and is easy to implement.However,as more samples are accepted,the area that remains uncovered by disks becomes smaller.It becomes ever more difficult to generate samples in these areas.This algorithm cannot guarantee that a maximal Poisson disk distribution can be generated,which also means that it is difficult to control termination of this algorithm.

Considerable efforts have been spent to improve the classic dart throwing approach.These new methods take advantage of spatial data structures to determine where to place the next dart[7-11].Graphics processing units(GPUs)can also be employed to improve the efficiency of the methods [12,13]. Ebeida et al.[14]and Gamito et al.[15]generalized the algorithm for Poisson disk distributions from 2D to higher dimensions.

Tile-based methods provide another approach to Poisson disk sampling.Dipp´e et al.[16]first proposed the idea of using pre-computed patterns called tiles for Poisson disk sampling.Subsequently many approaches have been proposed based on tiles,including Wang tiles[17],Penrose tiles[18], recursive Wang tiles[19],and polyominoes[20], etc.Such approaches are generally fast but rely on tiles with Poisson disk distributions to be calculated in advance.

Lloyd’s relaxation scheme[21]can also be used to produce point distributions with blue noise properties.McCool and Fiume[22]first used it to enhance blue noise properties of point sets.However, Balzer et al.[23]showed that this method often producesregularhexagonalpatterns,which is undesirable.Thus they improved Lloyd’s method by using the so called capacity constrained Voronoi tessellation(CCVT).This ensures that the Voronoi cell of each point has the same capacity,but the computation cost is much higher. Chen et al.[24] combined the CCVT[23]and CVT(centroidal Voronoi tessellation)[21]frameworks for blue noise sampling.De Goes et al.[25]formulated blue noise sampling in termsofoptimaltransport based on power diagram and Lloyd’s relaxation.In addition,to avoid patterns,they used a teleportation technique to locally perturb points.

In recent years,various methods have added controloverthespectralpropertiesofsample points[26-29].Ebeida et al.[30]proposed the notion of a well-spaced blue noise distribution.This is a distribution that both has the blue noise property and at the same time an improved spatial coverage ratio.Chen et al.[31]proposed a generalized form of blue noise whose samples can possess both spatial and non-spatial attributes.

2.2 Disk packing

Disk packing is a classical mathematical problem: the aim is to arrange multiple disks within a containing region without overlap between any two disks.Variants of the problem consider packing identicaldisks,and packing disksofdifferent sizes.For identical disk packing in the plane, it is well known that the densest arrangement is the regular hexagonal pattern,as conjectured by Kepler[32].Nevertheless,regular hexagonal packing is not the solution to the packing problem within a given container[33].Szab´o et al.[34]and Graham and Lubachevsky [35] discussed packing equal-sized disks into square and triangular containers.For the nonidentical disk packing problem,two kinds of methods exist: exact methods and heuristic methods.In exactmethods,nonlinear programming solvers such as MINOS[36],SNOPT[37],or MathOptimizer[38] are used to achieve numericallocalminima directly.Alternatively,various heuristic rules have been proposed to solve this problem,such as the maximal hole degree rule[39],corner-occupying actions[40],quasi-physical approaches[41],etc.

2.3 Image stippling

Image stippling isa way ofreproducing an image using small dots or stipples.Details of the image are represented through the intensity of the dots.In stippling,the distribution of the stipples has the Poisson disk property locally,and so related algorithms can be used to generate stippled images.For instance,Secord[3]used a centroidal Voronoi diagram to simulate a gray scale image.Deussen et al.[2]proposed a relaxation method using centroidal Voronoi diagram to generate approximations of blue noise distributions.Other work by Balzer et al.and others[23-25]gave extensions of algorithms for blue noise sampling.

3 Preliminaries

3.1 Disk packing problem

Given a region Ω∈R2and n diskswith known radiiwe focus on the disk packing problem of determining the tightest configuration for all the disks within Ω without overlap.Generally speaking,there are two types of disk packing algorithms depending on whether the given disks are identical or not.Poisson disk sampling takes advantage of identical disk packing while image stippling benefits from unequal disk packing.In this paper,we use the disk packing algorithms by Lu et al.[42].The basic idea is that we optimize the layout of the disks while shrinking or expanding them at the same rate. Thus,we introduce a scale factor k∈R+common to all disks, such that each disk Cibecomes kCiwith radius kri. The disk packing problem can thus be stated in the following form:

Maximize k

If all disks satisfy the above two constraints,we say that the configuration is valid.Note that a disk here is considered as being closed,so the second constraint can be rewritten aswhere xiis the centre of Ci.

3.2 Power diagram

The power diagram is a weighted form of the Voronoi diagram of a set of point sites.It is a partition of space into cells within which all points are closer to one of the sites than to all the other sites.

Intuitively,given a circle centered at piwith radius riand an outside point p,then the power of p with respect to the circle is defined as the square of the length of a line segment from p to a point q of tangency with the circle.As shown on the right,the power distance dw(p,pi)is thus defined as

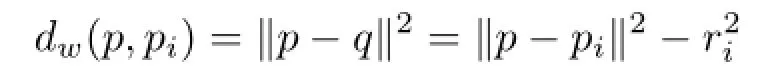
Regarding each circle center as a site,we treat each circle’s squared radius as a weight,that is wi=r2i,leading to the definition of the power diagram introduced by Aurenhammer[43].Given a set of distinct points P={p1,···,pn},in which each point piis associated with a weight wi≥0,then the power diagram of P is defined as the whole set of V(pi),where

V(pi)={p∈Rm|dw(p,pi)≤dw(p,pj),∀pj∈P} Given a bounded region Ω,let Ωi=V(pi)∩Ω be the intersection of V(pi)and Ω.The set of all Ωiconstitutes the bounded power diagram of P in Ω, where Ωiis called the cell for pi.If all the points have the same weight,the power diagram becomes the Voronoi diagram.

4 Disk packing algorithm for Poisson disk relaxation

Given a point distribution,whose Poisson disk radius is r0,we present a global relaxation scheme based on disk packing to improve the distribution by optimizing the point locations.The pseudocode for Poisson disk relaxation is given in Algorithm 1.Note that we restrict ourselves to periodic point sets,i.e.,point sets on the unit torus.

Algorithm 1:Poisson disk relaxation Input:A point distribution with n samplesin the bounded domain Ω. Output:An improved Poisson disk distribution. Steps:

1)Compute the normalized Poisson disk radius r, While r＜∈,do ·Construct the Voronoi diagram{Ωi}ni=1of{xi}ni=1inΩ; ·Foreach VoronoicellΩi,computeitsmaximal inscribed circle(MIC)centered on x˜i,{xi}ni=1 ←{x˜i}ni=1. 2)Return the improved Poisson disk distribution{xi}ni=1.

The disk packing relaxation is analogous to computing a centroidal Voronoi tessellation (CVT)[44]using Lloyd’s method to minimize a certain cost function.The idea is to iteratively update a Voronoi diagram in order to optimize the layout of the disks.Concretely,we iteratively compute the Voronoi diagram for the configuration and move each point to the center of the maximal inscribed circle of its corresponding Voronoi cell.Figure 1 illustrates successive improvements made by the disk packing iterations.

One must in principle be careful when a Voronoi diagram cell does not have a unique MIC.For example,if the cell is rectangular,there are infinitely many MICs that are copies of each other,sliding along the two long parallel edges.In this case,we simply pick an arbitrary MIC.Fortunately,this problem happens rarely in practice due to the numerical limitations.Therefore,we just assume that each Voronoi diagram cell has a unique MIC.

In each iteration,the algorithm aims to generate movements that enlarge the minimal MIC,leading to a monotonic increase in the normalized Poisson disk radius r,as shown in Fig.2.

The normalized Poisson disk radius is a measure of distribution quality,which is defined as the minimal distance between all points normalized by the radius of each disk in the densest layout, i.e.,a hexagonal layout.Lagae and Dutr´e[45] recommended it should be in the range[0.65,0.85].If the normalized Poisson disk radius is too large,more hexagonal structures will appear,which weakens the randomness property.On the contrary,too small normalized Poisson disk radius will also break the uniformity property.A suitable Poisson disk distribution will keep a good balance between the random and uniform properties.

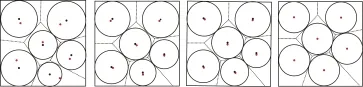
Fig.1 The disk packing process.Red dots indicate the current point positions;black circles and dots show the MICs and their centers respectively.

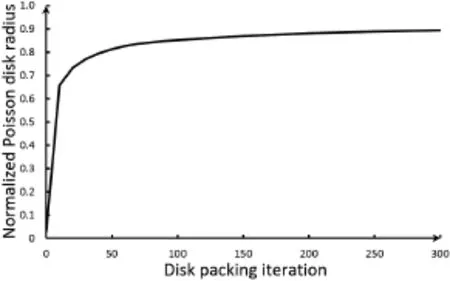
Fig.2 The normalized Poisson disk radiusincreases monotonically and converges during disk packing iterations.

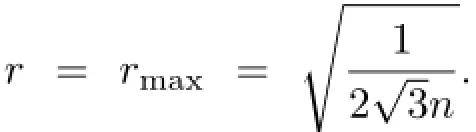
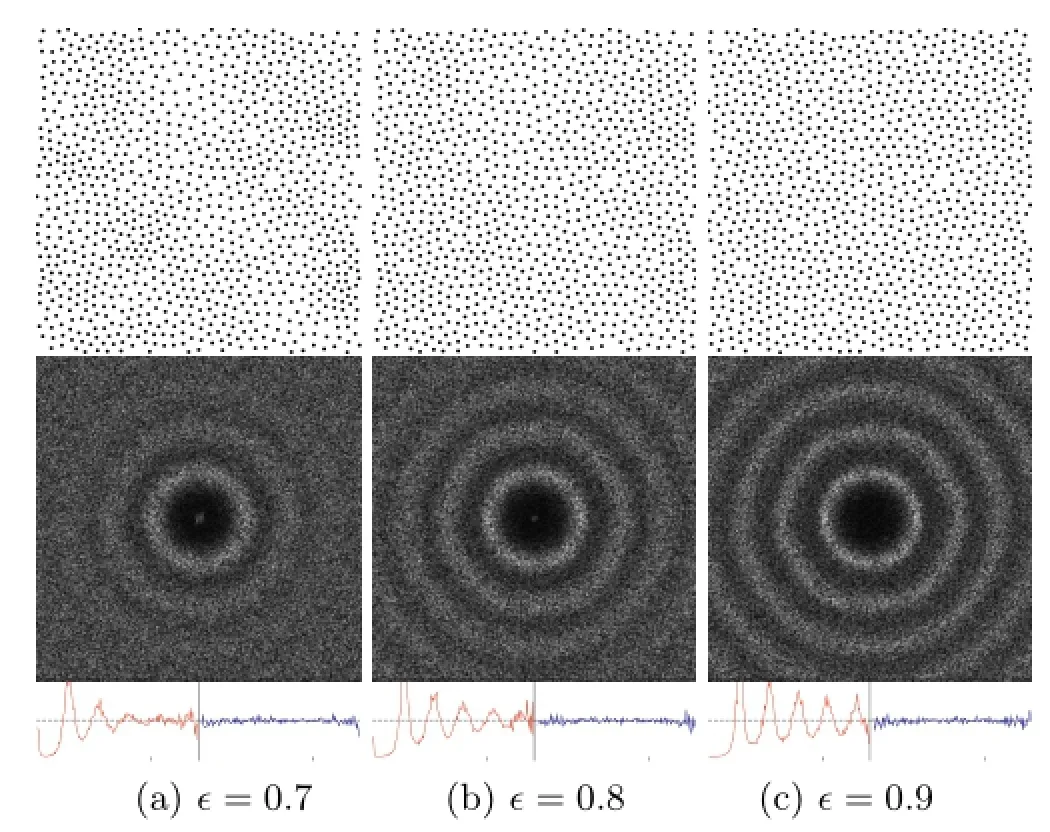
Fig.3 Results with different values of∈(1024 points).Upper row:the point distribution;lower row:spectral analysis of the point set.

Figure 4 shows an example of our method.Given the distribution(Fig.4(a))produced by Gamito and Maddock[15],we can further improve it(Fig.4(b)), to achieve a better balance between the random and uniform properties.

5 Image stippling

In this section,we replace the Voronoi diagram with the power diagram and thus extend our Poisson disk sampling method to image stippling based on the unequal disk packing problem.

Given a gray-scale image,we treat the intensity as the underlying density field of the domain and assign a weight for each sample point according to the density field.Specifically,for a sample point xiin the image domain,we first find the closest pixel to xi.Let its gray value be Ii∈[0,1].Then we assign a weight for xiequal towhere γ is a parameter for tuning the importance of image contrast and k is the scale factor introduced in Eq.(1).Thus the weighted point xiis regarded as a disk with radiusIn our experiments,we choose γ=3 to boost image contrast.

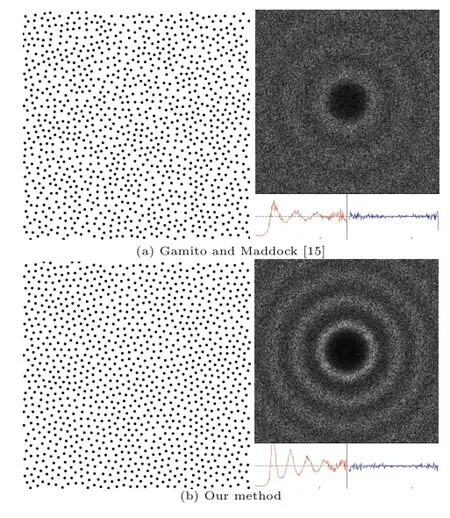
Fig.4 An example of our method,initialized by the result by Gamito and Maddock[15].We give the point distribution, mean periodogram,radial mean power,and an anisotropy analysis.Using the same number of points(n=1100),the Poisson disk radius is 0.012 and 0.013 for Gamito and Maddock’s result and ours respectively;the normalized Poisson disk radius is 0.73 and 0.80 respectively.

Given a gray-scale image(see Fig.5(a))and the desired number of points,we first generate an initial point distribution adapted to the image(see Fig.5(b))by use of error diffusion.During the weight assignment,we initialize the disks using a very small scale factor k=10−6,say,to guarantee that the disks do not overlap.During iteration,we recompute the power diagram and the MIC of each power cell, and update the positions of the points,together with k.

As the weight of each point changes with its location,this process is not guaranteed to converge. We use a threshold β to control the number of iterations.Selection of β depends on the number of samples,and should normally be chosen in the range[20,50].We note that the disk packing algorithm stops at a locally minimal configuration, in which small hole artifacts may exist,as shown in Fig.5(b).To eliminate such artifacts,we employ Lloyd relaxation to escape the local minimum (see Fig.5(c)).Pseudocode for image stippling is presented in Algorithm 2.

Algorithm 2:Image stippling via disk packing Input:A gray-scale image and the number of stipples n. Output:A stippling result with n points. Steps: 1)Generate the initial point configuration by error diffusion.k←10−6. 2)For i=1 to β ·Settheweightwiofeach stipplexiaccording to the density mapped from the gray value of its corresponding pixel.Set the disk radius of xias ri←√wi. ·Compute the bounded power diagram for{xi}ni=1and i=1. ·Compute the MIC for each power cell with center˜xi, radius Ri. ·Update{xi}n{wi}ni=1←{˜xi}ni=1. ·Update k←mini{Ri/ri}. 3)If the termination condition is not reached, run procedure Lloyd relaxation and goto step 2; Else output the point distribution.

Fig.5 Stippling process.Using the input image(a,top)as the underlying density map,we first generate an initial distribution of 5000 points via error diffusion(a,bottom).After disk packing and Lloyd relaxation iterations,we obtain the result in(d).

6 Result and comparisons

We have implemented our algorithm in C/C++ using CGAL[46]on an Intel Core i5 3.1 GHz 4GB RAM PC.One iteration of our algorithm includes the construction of a 2D Voronoi diagram or power diagram,in O(nlogn)time,and the computation of the maximal inscribed circle or the centroid for each cell,taking O(n)time.Therefore,each iteration of disk packing or Lloyd relaxation requires O(nlogn) time.

The time for Poisson disk sampling depends on the Poisson disk radius and the number of points.Each disk packing iteration takes 0.12s for 1100 points and 40 iterations are needed to generate the distributions.Figure 6 shows a result using the method of de Goes et al.[25]and the improved result achieved by our method.Figure 7 shows two results with more points than Fig.4.These two results preserve typical blue noise properties while keeping the same Poisson disk radius as Fig.4.Figure 7 indicates that given a Poisson disk distribution generated by other methods,we can achieve a better point set with more points while keeping the same Poisson disk radius(0.012)and preserving the blue noise properties.

In the image stippling experiments,it takes 1.65 s for one disk packing or Lloyd relaxation iteration for 30000 points(Fig.10),and 3.00 s for 50000 points (Figs.8 and 9).The number of iterations depends on the complexity of the input image and the number of samples.It requires 180 disk packing iterations and 30 Lloyd relaxation iterations to attain suitable results for Fig.8.Comparisons with state-of-the-art methods are shown in Figs.9 and 10.The close-up views in Fig.9 show that fewer regularity artifacts exist in our results.

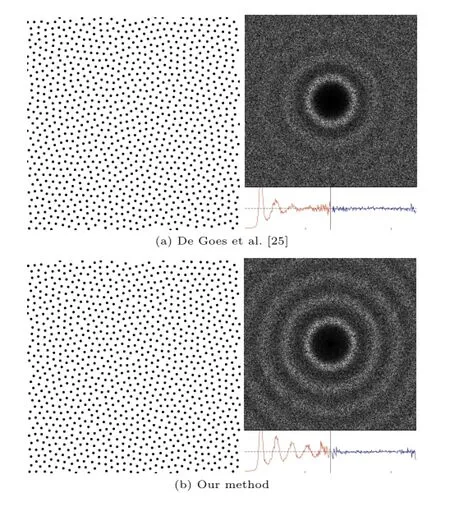
Fig.6 Comparisons of our method and the one in de Goes et al.[25].With the same number of points(n=1024),the Poisson disk radius is 0.0123 and 0.0135 for de Goes et al.’s result and ours respectively;the normalized Poisson disk radius is 0.74 and 0.80 respectively.Our result keeps the Poisson disk distribution properties well.

7 Conclusions

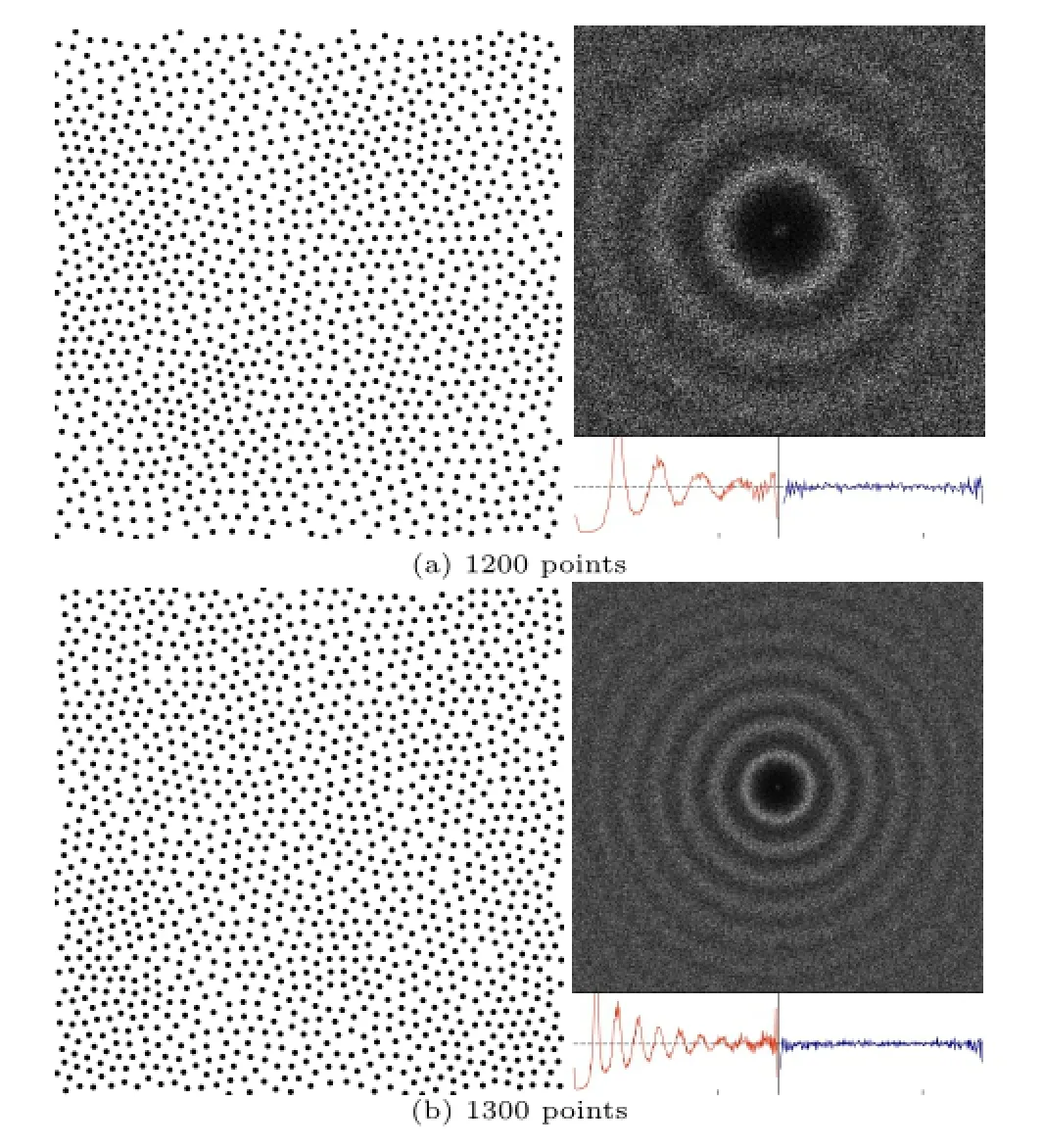
Fig.7 For the same Poisson disk radius(0.013)as shown in Fig.4(b),our method can incorporate more points.The numbers of points in(a)and(b)are 1200 and 1300 respectively.The normalized Poisson disk radius for(a)and(b)is 0.78 and 0.80 respectively.

In thispaper,weobservethatadensedisk packing configuration naturally satisfies the desirable properties of Poisson disk distributions.We take advantage of this to propose a novel relaxation scheme for Poisson disk sampling which achieves a good balance between randomness and uniformity. Our relaxation method can generate Poisson disk distributions with more points than current methods fora given Poisson disk radius.Applications including rendering,imaging,and texture generation can benefit from this improvement.Furthermore,we adapt the Poisson disk sampling algorithm to image stippling by extending identical disk packing to unequal-sized disks.This generates stippling results with fewer regularity artifacts than other methods.

One limitation,is that our method for stippling is not good at preserving sharp features in the input images,as can be seen in Fig.9.This is because the disk packing process tends to decentralize the disks to optimize space coverage.In our future work,we hope to use disk packing to achieve good stippling results while preserving features.It is also promising to study sphere packing approach for 3D Poisson sphere sampling and the acceleration of the approach by use of GPUs.

Acknowledgements

The authors would like to acknowledge the help of

Fig.8 Image stippling.(a)Input image;(b)initial point set obtained by error diffusion(50000 points);and(c)our result.

Prof.Wenping Wang for many valuable discussions on this work.This work was supported in part by National Natural Science Foundation of China (Nos.61202147 and 61272243),Shandong Province Natural Science Foundation(No.ZR2012FQ026), and Fundamental Research Funds for the Central Universities(No.20720140520).

Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use,distribution,and reproduction in any medium,provided the original author(s)and the source are credited.

[1]Pharr, M.; Humphreys, G.Physically Based Rendering: From Theory to Implementation.SanFrancisco,CA,USA:Morgan Kaufmann Publishers Inc.,2004.

Fig.9 Image stippling.(a)and(b)Input image and initial point set(50000 points)respectively;(c)result of the method in de Goes et al.[25];and(d)our result.

[2]Deussen,O.;Hiller,S.;Van Overveld,C.;Strothotte, T.Floating points:A method for computing stipple drawings.Computer Graphics Forum Vol.19,No.3, 41-50,2000.

[3]Secord, A. Weighted Voronoi stippling. In: Proceedingsofthe2nd internationalsymposium on Non-photorealistic animation and rendering, 37-43,2002.

[4]Deussen,O.;Hanrahan,P.;Lintermann,B.;Mh, R.;Pharr,M.;Prusinkiewicz,P.Realistic modeling and rendering of plant ecosystems.In:Proceedings of the 25th annual conference on Computer graphics and interactive techniques,275-286,1998.

[5]Surazhsky,V.;Alliez,P.;Gotsman,C. Isotropic remeshing of surfaces: A local parameterization approach.In:12th International Meshing Roundtable, 215-224,2003.

[6]Cook, R.L.Stochastic sampling in computer graphics.ACM Transactions on Graphics Vol.5,No.1, 51-72,1986.

[7]Jones, T.R.Efficient generation of Poisson-disksampling patterns.Journal of Graphics,GPU,and Game Tools Vol.11,No.2,27-36,2006.

[8]Dunbar,D.;Humphreys,G.A spatial data structure for fast Poisson-disk sample generation.ACM Transactions on Graphics Vol.25,No.3,503-508, 2006.

[9]White,K.B.;Cline,D.;Egbert,P.K. Poisson disk point sets by hierarchical dart throwing.In: IEEE Symposium on Interactive Ray Tracing,129-132,2007.

[10]Ebeida,M.S.;Davidson,A.A.;Patney,A.;Knupp, P.M.;Mitchell,S.A.;Owens,J.D.Efficient maximal Poisson-disk sampling.In:ACM SIGGRAPH 2011 papers,Article No.49,2011.

[11]Yan,D.-M.;Wonka,P.Gap processing for adaptive maximal Poisson-disk sampling.ACM Transactions on Graphics Vol.32,No.5,Article No.148,2013.

[12]Wei,L.-Y.Parallel Poisson disk sampling.In:ACM SIGGRAPH 2008 papers,Article No.20,2008.

[13]Xiang,Y.;Xin,S.-Q.;Sun,Q.;He,Y. Parallel and accurate Poisson disk sampling on arbitrary surfaces.In:SIGGRAPH Asia 2011 Sketches,Article No.18,2011.

[14]Ebeida,M.S.;Mitchell,S.A.;Patney,A.;Davidson, A.A.;Owens,J.D.A simple algorithm for maximal Poisson-disk sampling in high dimensions.Computer Graphics Forum Vol.31,No.2,785-794,2012.

[15]Gamito, M.N.; Maddock, S.C. Accurate multidimensional Poisson-disk sampling. ACM Transactions on Graphics Vol.29,No.1,Article No.8,2009.

[16]Dipp´e,M.A.Z.; Wold,E.H. Antialiasing through stochastic sampling.In:Proceedings of the 12th annual conference on Computer graphics and interactive techniques,69-78,1985.

[17]Cohen,M.F.;Shade,J.;Hiller,S.; Deussen, O.Wang tiles for image and texture generation.ACM Transactions on Graphics Vol.22,No.3,287-294, 2003.

[18]Ostromoukhov,V.;Donohue,C.;Jodoin,P.-M.Fast hierarchical importance sampling with blue noise properties.ACM Transactions on Graphics Vol.23, No.3,488-495,2004.

[19]Kopf,J.;Cohen-Or,D.;Deussen,O.;Lischinski, D.Recursive Wang tiles for real-time blue noise.ACM Transactions on Graphics Vol.25,No.3,509-518, 2006.

[20]Ostromoukhov,V.Sampling with polyominoes.ACM Transactions on Graphics Vol.26,No.3,Article No.78,2007.

[21]Lloyd,S.Least squares quantization in pcm.IEEE Transactions on Information Theory Vol.28,No.2, 129-137,1982.

[22]McCool,M.;Fiume,E.Hierarchical Poisson disk sampling distributions.In: Proceedings ofthe conference on Graphics interface,94-105,1992.

[23]Balzer,M.;Schl¨omer,T.;Deussen,O.Capacityconstrained point distributions:A variant of Lloyd’s method.ACM Transactions on Graphics Vol.28, No.3,Article No.86,2009.

[24]Chen, Z.; Yuan, Z.; Choi, Y.-K.; Liu, L.; Wang,W.Variational blue noise sampling.IEEE Transactions on Visualization and Computer Graphics Vol.18,No.10,1784-1796,2012.

[25]De Goes, F.; Breeden, K.; Ostromoukhov, V.; Desbrun, M.Blue noise through optimal transport.ACM Transactions on Graphics Vol.31, No.6,Article No.171,2012.

[26]Zhou,Y.;Huang,H.;Wei,L.-Y.;Wang,R.Point sampling with general noise spectrum. ACM Transactions on Graphics Vol.31,No.4,Article No.76,2012.

[27]¨Oztireli,A.C.;Gross,M.Analysis and synthesis of point distributions based on pair correlation.ACM Transactions on Graphics Vol.31,No.6,Article No.170,2012.

[28]Heck,D.;Schl¨omer,T.;Deussen,O.Blue noise sampling with controlled aliasing.ACM Transactions on Graphics Vol.32,No.3,Article No.25,2013.

[29]Wachtel,F.;Pilleboue,A.;Coeurjolly,D.;Breeden, K.;Singh,G.;Cathelin,G.;de Goes,F.;Desbrun,M.; Ostromoukhov,V.Fast tile-based adaptive sampling with user-specified Fourier spectra.ACM Transactions on Graphics Vol.33,No.4,Article No.56,2014.

[30]Ebeida,M.S.;Awad,M.A.;Ge,X.;Mahmoud,A.H.; Mitchell,S.A.;Knupp,P.M.;Wei,L.-Y.Improving spatial coverage while preserving the blue noise of point sets.Computer-Aided Design Vol.46,25-36, 2014.

[31]Chen,J.;Ge,X.;Wei,L.-Y.;Wang,B.;Wang,Y.; Wang,H.;Fei,Y.;Qian,K.-L.;Yong,J.-H.Wang, W.Bilateral blue noise sampling.ACM Transactions on Graphics Vol.32,No.6,Article No.216,2013.

[32]Kepler,J.The Six-Cornered Snowflake.Oxford,UK: Clarendon Press,1966.

[33]Lubachevsky,B.D.;Graham,R.L.Curved hexagonal packingsofequaldisksin a circle.Discrete& Computational Geometry Vol.18,No.2,179-194, 1997.

[34]Szab´o,P.G.;Mark´ot,M.Cs.;Csendes,T.;Specht,E.; Casado,L.G.;Garc´ıa,I.New Approaches to Circle Packing in a Square:With Program Codes.New York, NY,USA:Springer-Verlag,2007.

[35]Graham,R.L.;Lubachevsky,B.D.Dense packings of equal disks in an equilateral triangle:From 22 to 34 and beyond.The Electronic Journal of Combinatorics Vol.2,No.1,A1,1995.

[36]Birgin,E.G.;Sobral,F.N.C.Minimizing the objectdimensionsin circle and sphere packing problems. Computers and Operations Research Vol.35,No.7,2357-2375,2008.

[37]Addis,B.;Locatelli,M.;Schoen,F.Efficiently packing unequal disks in a circle.Operations Research Letters Vol.36,No.1,37-42,2008.

[38]Pint´er, J.D.; Kampas, F.J.MathOptimizer professional: Key features and illustrative applications. In: Nonconvex Optimization and Its Applications,Vol.84 Global Optimization.Liberti, L.;Maculan,N.Eds.New York,NY,USA:Springer-Verlag,263-279,2006.

[39]Huang,W.Q.;Li,Y.;Akeb,H.;Li,C.M.Greedy algorithms for packing unequal circles into a rectangular container.Journal of the Operational Research Society Vol.56,No.5,539-548,2005.

[40]L¨u,Z.;Huang,W.PERM for solving circle packing problem.Computers&Operations Research Vol.35, No.5,1742-1755,2008.

[41]Wang,H.;Huang,W.;Zhang,Q.;Xu,D.An improved algorithm for the packing of unequal circles within a larger containing circle.European Journal of Operational Research Vol.141,No.2,440-453,2002. [42]Lu,L.;Choi,Y.-K.;Sun,F.;Wang,W.Variational circle packing based on power diagram.Technical report.The University of Hong Kong,2011.Available at http://vr.sdu.edu.cn/～lulin/CP TechReport.pdf.

[43]Aurenhammer,F.Powerdiagrams: Properties, algorithms and applications.SIAM Journalon Computing Vol.16,No.1,78-96,1987.

[44]Liu,Y.;Wang,W.;L´evy,B.;Sun,F.;Yan,D.-M.; Lu,L.;Yang,C.On centroidal voronoi tessellation—energy smoothnessand fastcomputation.ACM Transactions on Graphics Vol.28,No.4,Article No.101,2009.

[45]Lagae,A.;Dutr´e,P.A comparison of methods for generating Poisson disk distributions.Computer Graphics Forum Vol.27,No.1,114-129,2008.

[46]Fabri,A.;Pion,S.CGAL:Thecomputational geometry algorithms library.In:Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems,538-539,2009.

[47]Schmaltz,C.;Gwosdek,P.;Bruhn,A.;Weickert, J.Electrostatic halftoning.Computer Graphics Forum Vol.29,No.8,2313-2327,2010.

[48]Fattal,R.Blue-noise point sampling using kernel density model.ACM Transactionson Graphics Vol.30,No.4,Article No.48,2011.

Guanghui Liang received the BSEE degree in computer science and technology from Shandong University, China,in 2012.Currently,he is studying at Shandong University for a master’s degree.His research interests include computer graphics, computational geometry,and visualization.

Lin Lu is an associate professor of computer science in Shandong University, China. She got her B.Eng.(2002) and M.Eng.(2005) degrees in Shandong University,and Ph.D.(2011)degree in the University of Hong Kong, allin computer science.Her research interests include computer graphics and geometry processing.

ZhongguiChen received B.S.and Ph.D.degrees in applied mathematics from Zhejiang University, in 2004 and 2009,respectively.Currently,he is working as an associate professor in the Department of Computer Sciences,School of Information Science and Technology,Xiamen University, China.His research interests include computer graphics and computational geometry.

Chenglei Yang isa professorat Shandong University,China.He holds a Ph.D.degree in computer science from Shandong University.His interests includehuman-computerinteraction, virtual reality,computational geometry, and computer graphics.His work involves a variety of research topics such as data modeling and rendering,visibility computing, path planning,collision detection,cooperative design,and interaction in the domains of immersive learning systems.

1School of Computer Science and Technology, Shandong University,Jinan 250101,China.E-mail: ghliang.sdu@gmail.com,llu@sdu.edu.cn(),chl yang@ sdu.edu.cn.

2Department of Computer Science,Xiamen University, Xiamen 361005,China.E-mail:chenzhonggui@xmu. edu.cn.

Manuscript received:2014-09-19;accepted:2015-01-12