中国股市整合风险测度研究——基于VaR框架和相关结构的分析

覃小兵，唐晓华，林 宇

（1.成都理工大学 商学院，成都 610059；2.四川工商职业技术学院，四川 都江堰 611830）

中国股市整合风险测度研究
——基于VaR框架和相关结构的分析

覃小兵1，唐晓华2，林 宇1

（1.成都理工大学 商学院，成都 610059；2.四川工商职业技术学院，四川 都江堰 611830）

针对现有流动性风险与市场风险的整合风险测度方法忽略两者相关结构的问题，在运用ARMA-GARCH-t模型对中国股市市场风险因子和流动性风险因子的边缘分布进行刻画的基础上，引入7种Copula函数来考察两者的相关结构，并运用MonteCarlo方法测度出整合风险。以沪深300指数为研究对象的实证检验结果表明：中国股市市场风险与流动性风险之间更符合动态的相关结构；在考虑了两风险的相关结构之后，基于时变t Copula函数的风险测度模型最能准确测度两风险的整合风险。

整合风险；流动性风险；市场风险；Copula函数；蒙特卡洛模拟

一、文献综述

美国次贷危机、欧洲债务危机等一系列金融风险事件的爆发，使得流动性风险成为继市场风险之后学者及风险管理者关注的焦点。对流动性风险进行管理已成为金融风险管理者不得不面对的事情，而且，在市场缺乏流动性的情况下，流动性风险能够显著增大市场风险，加剧市场波动[1]。因此，如何加强对流动性风险的管理，尤其是加强对流动性风险与市场风险整合风险的管理，成为投资者及金融风险管理者亟待解决的问题。

目前，虽然VaR技术已经成为测度市场风险的通用方法，并被广泛运用于实践，但是如何准确测度市场风险与流动性风险的整合风险还没有一个被广泛认可的方法。尽管如此，由Bangia et al提出的基于价差调整VaR的BDSS模型[2]，即在传统市场风险上加上由价差测得的流动性风险，成为当前学者在研究流动性风险与市场风险的整合风险时较多采纳的模型。该模型不仅测度了市场风险的VaR值，更为重要的是，它在传统市场风险的基础上考虑了流动性风险的影响，从而更为全面、综合地反映了投资者及风险管理者所面临的风险。正是BDSS模型的这些优点，其一经提出就受到诸多学者的关注并在其基础上进行扩展研究，如Angelidis et al[3]及刘晓星等[4]。然而，不可忽视的是，虽然BDSS模型整合了流动性风险与市场风险，但仅是将两者简单地相加，而这种方法只能在流动性风险与市场风险完全正相关的情况下才能成立[5]。遗憾的是，这种将两类风险假定为完全正相关的假设过于简单，而现实中的情况却更为复杂[1][5]，因而BDSS模型并不能完全准确地反映出市场风险与流动性风险之间的相关结构。值得庆幸的是，这种复杂的相关结构能够用一个合适的Copula函数来准确描述[6][7]。于是，本文引入Copula函数来刻画流动性风险与市场风险之间的相关结构，进而准确测度两者的整合风险。

然而，选择何种Copula函数来描述中国股市流动性风险与市场风险之间的相关结构，不同的学者有不同的看法。张金清等认为运用静态的正态Copula函数就能准确刻画市场风险与流动性风险之间的相关结构；然而，张蕊等则认为运用Frank Copula函数才能够准确刻画市场风险与流动性风险之间的相关结构；江红莉等则认为时变的Copula函数（Time-varying Copula）比静态的Copula函数更能准确刻画流动性风险与市场风险之间的相关结构[8]。因此，为准确刻画中国股市流动性风险与市场风险之间的相关结构，本文将学者们较常运用的5种静态Copula函数以及时变的正态Copula函数和时变t Copula函数用于考察流动性风险与市场风险的相关结构，并试图找出能准确描述中国股市流动性风险与市场风险相关结构的最优Copula函数，以便运用蒙特卡洛（Monte Carlo）模拟方法来拟合整合风险的分布，进而准确测度整合风险的VaR值。

需指出的是，流动性风险因子的选择对于准确刻画流动性风险与市场风险相关结构有着重要影响[5]。目前，对于流动性风险的刻画因子也并没有一个统一的指标，如张金清等运用单位换手率引起的每股交易价格变化率作为流动性风险因子；而张蕊等则选用的是相对价差指标；张铮等研究得出，Amihud指标是较优的低频流动性间接指标[9]。然而，Andreas及王明涛等指出，Amihud指标没有考虑资产流通盘的大小，从而容易受到资产流通总额的影响，并建议运用日换手率来代替原指标中的成交金额，并且指出修正过后的Amihud指标是一个较好的流动性指标[10][11]。因此，本文选择修正后的Amihud指标作为流动性风险因子。

毋庸置疑，模型的稳健性检验作为风险测度的重要环节，关系到风险管理的成败。然而，以往学者在对整合风险测度模型的稳健性进行评价时都是以失败率作为评价模型的标准[1][4]，而忽略了模型失败情况的随机性。作为风险管理者，除了要保证风险测度的准确性之外，还要避免出现连续发生风险溢出的情况，即风险的溢出情况尽可能是独立的[12]。因而，若仅以失败率作为评价模型稳健性的标准可能缺乏严谨。于是，本文运用既检验模型预测失败率与假定失败率是否一致，又检验失败情况是否具有随机性的Kupiec[13]和Christofersen[14]返回测试（Backtesting）方法对模型的稳健性进行检验，以使检验结果更具有科学性和可信性。

基于以上分析，本文选择修正后的Amihud指标作为流动性风险的风险因子，并选用5种静态Copula函数和2种时变Copula函数来刻画其与市场风险因子之间的相关结构；进而运用蒙特卡洛模拟法，模拟出既符合两风险相关结构特征又具有原市场风险因子及流动性风险因子特征的随机数并得到整合风险的分布情况，进而测度出整合风险的VaR值；最后运用规范的Back-testing检验方法对模型的稳健性进行检验。

最后，仍需指出的是，虽然已有诸多学者（如，Bangia et al、Angelidis et al、Loebnitz[15]、刘晓星等以及林辉[16]）研究了市场风险与流动性风险的整合风险，并证实了在测度金融市场风险时不仅不能忽略流动性风险，而且当市场缺乏流动性时，流动性风险的增大，往往伴随着市场风险也显著增大。但是，他们的研究并没有阐明市场风险与流动性风险之间的相关结构。虽然，张金清等、张蕊等以及江红莉等运用Copula函数考察了市场风险与流动性风险的相关结构，但是，他们的研究限于单一地运用静态模型或是时变模型，具有一定的片面性，而本文则是将静态模型和时变模型一并纳入考虑，更全面地考察中国股市市场风险与流动性风险之间的相关结构。同时与前人研究选取相对价差作为流动性风险因子不同的是，本文引入较好的低频流动性指标——修正后的Amihud指标作为流动性风险的风险因子；而且更为重要的是，本文对模型的稳健性检验，并没有把以往学者采用的失败率作为模型稳健性的评价标准，而是采用规范的Back-testing方法对模型的稳健性进行检验。

二、研究方法

（一）基于相关结构与Monte Carlo法的整合风险VaR测度方法

在金融风险管理中，市场风险因子通常用对数收益率来表示。

对于流动性风险因子l，目前还没有一个统一的度量指标。张铮等研究得出Amihud指标是一个很好的低频流动性指标。然而，Andreas、张金清等以及王明涛等指出，Amihud指标没有考虑资产流通盘的大小，从而容易受到资产流通总额的影响，并建议用日换手率来代替原指标中的成交金额。于是，本文将运用修正后的Amihud指标——lAs作为流动性风险的风险因子。

其中，turnovert为金融资产的日换手率，且其值为金融资产第t日的成交股数Volt与其第t日的流通股数ANt的比值，即turnovert=Volt/ANt。因此，流动性风险因子lAs，t可以理解为，单位换手率所引起的收益变化，可以用来反映流动性风险的大小，即lAs，t越小，则流动性越好，流动性风险越小，反之亦然。于是，在t时刻成交流通中的m个单位的头寸所引起的流动性风险即为mt×lAs，t，其中mt=nt/ANt，nt为投资者欲成交的头寸。

至此，我们得到市场风险因子与流动性风险因子。此外，在金融风险管理中还通常假定金融资产收益率服从如下的波动形式：

当然，要准确测度流动性风险与市场风险的整合风险，则需要运用Copula函数对市场风险与流动性风险的相关结构进行考察。需指出的是，运用Copula函数来考察市场风险与流动性风险之间的相关结构，两风险因子需满足服从[0，1]均匀分布的条件，而通常它们并不满足这一条件，因而需要将两风险因子进行标准化及概率积分变换（Probability Integral Transform，PIT），将其转换为服从[0，1]上的均匀分布，标准化过程如下：

其中，i为市场风险因子rt或流动性风险因子lt。

从（4）式可知，要得到标准市场风险因子zr，t及标准流动性风险因子zl，t，首先必须运用合适的均值方程及波动模型分别对市场风险因子rt和流动性风险因子lt进行建模，估计出两者的条件均值t和条件标准差t。鉴于金融时间序列通常具有自相关性、异方差性等特征，因而在此运用ARMA-GARCH模型来刻画市场风险因子与流动性风险因子的自相关性及异方差性等特征。考虑到金融时间序列通常具有比正态分布更厚的尾部，同时Giot指出运用GARCH-t模型对金融风险进行刻画，能取得很好的效果[17]，因此，本文运用ARMA-GARCH-t模型对市场风险因子与流动性风险因子进行建模。ARMAGARCH-t模型的基本形式如下：

至此，我们估计出了流动性风险因子与市场风险因子的条件均值t、条件标准差t，进而得到标准市场风险因子zr，t和标准流动性风险因子zl，t。通过对标准市场风险因子zr，t和标准流动性风险因子zl，t进行概率积分变换，得到服从[0，1]均匀分布的市场风险因子Ut与流动性风险因子Vt。于是，可以运用Copula函数来考察市场风险因子Ut与流动性风险因子Vt之间的相关结构。

为准确反映市场风险因子Ut与流动性风险因子Vt的相关结构，本文采用5种常用的静态Copula函数来考察两者的静态相关结构，同时采用Patton基于Hansen自回归条件密度的思想而提出的时变正态Copula函数和时变t Copula函数来刻画两者的动态相关结构[18][19]。两时变Copula函数的分布函数及相关系数演进模型如下所示：

（1）时变正态Copula函数的分布函数及相关系数方程：

当n=2时，

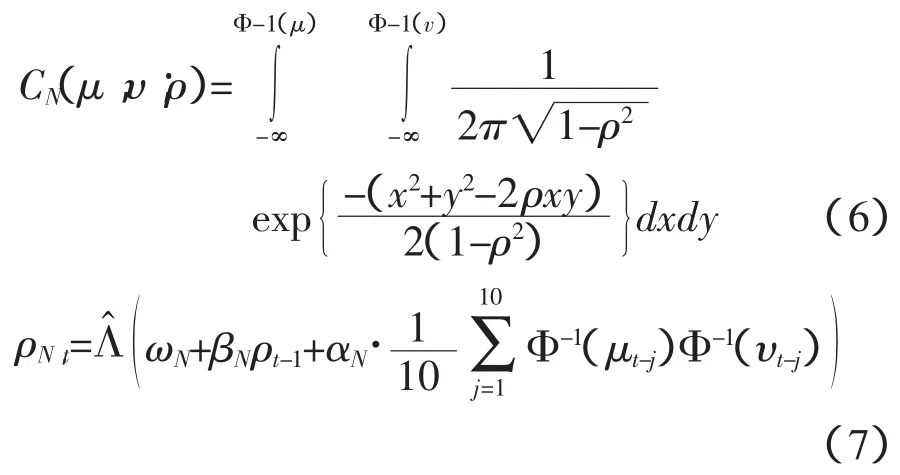
（2）时变t Copula函数的分布函数及相关系数方程：

当n=2时，

至此，得到了市场风险因子Ut与流动性风险因子Vt的相关结构，进而运用蒙特卡洛模拟方法模拟出既满足市场风险因子Ut与流动性风险因子Vt相关结构，又具有风险因子rt及lt特征的随机变量r，t和l，t。将得到的条件均值t和条件标准差t以及随机变量r，t和l，t代入（3）式中，进而估计出符合流动性风险与市场风险相关结构的风险因子t和t，将t和t代入整合风险因子Rz，t中：

至此，我们得到了基于相关结构的整合风险在第t时刻的一种分布情况。重复进行j次（此处j= 5000）蒙特卡洛模拟，则可得到在第t时刻整合风险因子Rz，t的j种分布情况。

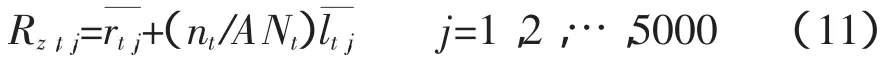
再将整合风险因子Rz，t在第t时刻的j种分布情况按升序排列，通过求排序后的整合风险因子z，t，j在置信水平q下的分位数，从而得到整合风险Rz，t在第t时刻及置信水平q下的VaR值，即

（二）VaR测度方法的Back-testing检验方法

本文运用Kupiec的检验方法对整合风险的稳健性进行检验。根据Kupiec et al的研究成果，给定的置信水平为q，考察期为N，实际失败天数为n，则失败率或溢出率为（n/N）。模型的零假设为：溢出率（n/N）=（1-q），进而模型的稳健性检验就转换成检验溢出率（n/N）是否与预期溢出率（1-q）有显著差异。其中，当VaR值小于资产的真实损失时，说明预测的风险不足以覆盖市场发生的风险，则定义为预测失败，并用指示变量I来表示，否则为预测成功。

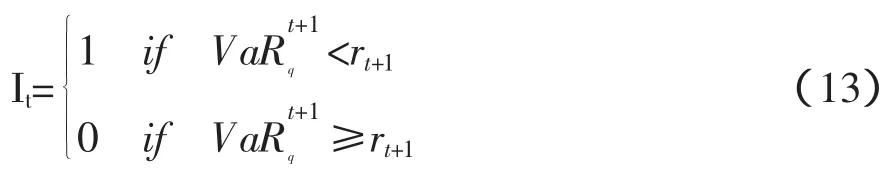
此外，根据Kupiec et al的研究成果，模型零假设的似然比LRuc满足（14）式，并且依概率服从自由度为1的卡方分布。

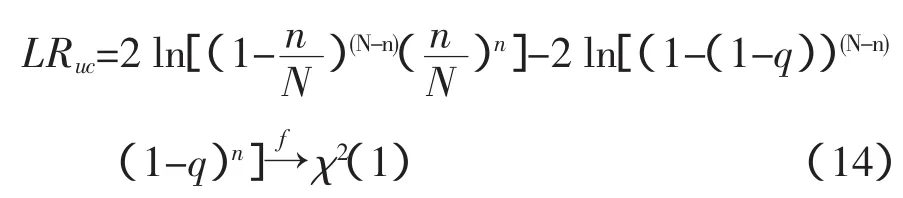
通常为了便于比较，我们将LRuc的卡方值转换成概率值Puc。

若Puc＞（1-q），则不能拒绝零假设，即认为风险模型在置信水平q下是可靠的，且Puc值越接近于1，说明模型预测的效果越好。

倘若仅仅检验模型的溢出率与预期溢出率是否相符，并不能说明模型是稳健的，还必须对模型溢出情况的随机性进行检验。于是，Christoffersen构建了类似于LRuc的检验指标LRind，来检验溢出情况的随机性，其似然比如下：

在此基础上，Christoffersen还构建了一个综合了指标LRuc和指标LRind的条件检验指标LRcc，以综合反映模型的稳健性。LRcc指标依概率服从自由度为2的卡方分布，且其似然比满足：

由于检验指标LRcc综合了指标LRuc和指标LRind，从而有更强的检验能力。于是，本文判断模型稳健性的主要依据是该指标对应的概率值Pcc。

三、实证结果及分析

（一）研究样本

本文选取在中国股票市场上具有代表性的沪深300指数作为研究对象，并选取2009年1月5日至2014年3月31日作为样本期，进而得到在该样本期内的样本点，共计1269个。需说明的是，在本文所选的样本期内，沪深300指数的日成交股数在2亿股到20亿股之间，因此本文假定沪深300指数的日成交股数为2亿股。本文所需的研究数据来自上海证券交易所对外公布的《上证统计月报》和锐思金融数据库。本文主要运用的分析软件为matlab 2013b。

（二）市场风险因子及流动性风险因子的特征检验及分析

图1是沪深300指数市场风险因子r及流动性风险因子l的波动情况。从图1可以明显地观察到两因子均具有较大的波动性；同时也表现出了明显的“波动聚集性”，即在较大的波动后又伴随着另一较大的波动，在较小的波动后也伴随着另一较小的波动。表1为市场风险因子r及流动性风险因子l的描述性统计检验结果。从表1可知：市场风险因子r正态分布检验的J-B统计量在1%的显著性水平下显著拒绝服从正态分布的假设；其峰度（Kurtosis）和偏度（Skewness）反映出市场风险因子r具有“尖峰”及“有偏”的分布特征；单位根检验和拉格朗日乘数检验也均在1%的显著性水平下显著拒绝零假设，说明市场风险因子r不存在单位根，但具有“异方差”特征；自相关性检验在1%的显著性水平下不拒绝零假设，表明市场风险因子r为非自相关序列。因而，沪深300指数的市场风险因子r为“尖峰”、“有偏”、具有“异方差性”的平稳序列。流动性风险因子l的特征检验，除了拉格朗日乘数检验和“异方差性”检验的结果与市场风险因子r的检验结果不同之外，其余检验结果与市场风险因子r的检验结果相似。与市场风险因子r相比，流动性风险因子具有更明显的“尖峰”及“有偏”分布特征。因此，根据两风险因子的上述分布特征，可分别采用GARCH模型和ARMA模型对市场风险因子r及流动性风险因子l进行建模分析。

表1 市场风险因子与流动性风险因子的描述性统计检验结果

（三）市场风险因子与流动性风险因子的边缘分布参数估计结果

基于市场风险因子r及流动性风险因子l的特征检验结果，并结合AIC准则，最终选择GARCH（1，1）-t模型对市场风险因子r的边缘分布进行建模，以及选取ARMA（7，5）-t模型对流动性风险因子进行建模，参数估计结果如表2、表3所示。

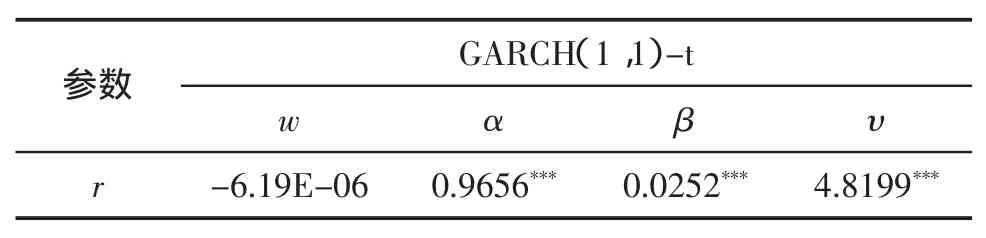
表2 市场风险因子的边缘分布参数估计结果

表3 流动性风险因子的边缘分布参数估计结果

从表2，表3可以看出，市场风险因子r的持久性因子（α+β）为0.9908，非常接近于1，说明其波动效应具有持久性；市场风险因子r及流动性风险因子l的自由度υ分别为4.8199和2.3096，并且在1%的置信水平下显著，说明两者均具有较厚的尾部。此外，为检验所选模型对市场风险因子和流动性风险因子“异方差性”特征及“自相关性”特征的刻画效果，以及检验标准化后的市场风险因子zr和流动性风险zl是否满足标准残差序列服从独立同分布（Independent Identically Distribution，i.i.d）的要求，因而对标准化后的市场风险因子zr和流动性风险zl再次进行描述性统计检验，特征检验结果如表4所示。

表4 标准市场风险因子与标准流动性风险因子的特征检验结果

从表4的检验结果可看出，虽然标准化后的市场风险因子zr与标准流动性风险因子zt仍具有“尖峰”、“有偏”的分布特征，但是两者均已不再具有“异方差性”及“自相关性”特征，由此可见，本文所运用的GARCH（1，1）-t模型以及ARMA（7，5）-t模型分别对市场风险因子r和流动性风险因子l的“异方差性”及“自相关性”特征进行刻画是合理的；同时从BDS统计量来看，两者均在1%的置信水平下不拒绝零假设，说明标准化后的两风险因子均为独立同分布序列。因而标准化后的两风险因子为“尖峰”、“有偏”、“无自相关性”和“异方差性”的独立同分布平稳序列，进而说明本文采用的均值方程及波动模型能够有效地刻画两风险因子的分布特征。

（四）Copula函数的参数估计结果及分析

为准确刻画我国股市市场风险与流动性风险之间的相关结构，本文选择5种常用的静态Copula函数来考察两风险之间的静态相关结构，以及采用时变正态Copula函数和时变t Copula函数来刻画两风险之间的动态相关结构。其中，5种静态Copula函数的相关参数估计结果如表5所示；两种动态Copula函数的参数估计结果如表6所示；同时，两风险之间的动态相关性如图2所示。

表5 静态Copula函数的相关参数估计结果

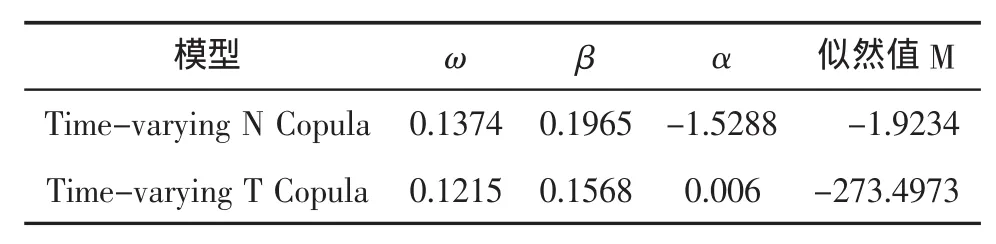
表6 时变Copula函数的相关参数估计结果

图2 时变Copula函数的相关系数

从表5可看出，在静态的Copula模型中，静态t Copula函数的似然值最小，其次是Gumbel Copula函数，最大的则是Clayton Copula函数，因此，从似然值指标来看，静态t Copula函数比其他静态Copula函数更能刻画我国市场风险与流动性风险之间的相关结构。另外，由于正态Copula函数与t Copula函数的相关参数亦是变量间的线性相关系数，而表5中正态Copula函数与t Copula函数的线性相关系数均不为1，则说明中国股市的市场风险与流动性风险之间并非完全正相关，从而说明若仍旧按照Bangia et al的做法，将流动性风险与市场风险进行简单相加来测度两者的整合风险，而不考虑这两者之间的相关结构是不够严谨的。因此，要准确测度市场风险与流动性风险的整合风险，就必须考虑两者之间的相关结构。

从表5和表6中各模型的似然值来看，时变t Copula函数的似然值比最优的静态t Copula函数的似然值更小，说明运用时变Copula函数描述的动态相关结构更符合我国股市市场风险与流动性风险的相关结构；同时时变t Copula函数的似然值也比时变正态Copula函数的似然值更小。因而说明我国股市的流动性风险与市场风险间的动态相关结构运用时变t Copula函数来描述更为准确。

从图2可以看出，无论是用时变正态Copula函数还是用时变t Copula函数来描述我国股市市场风险与流动性风险的动态相关结构，均得出两者的相关性不为1且基本在区间[-0.05，0.15]上，因而再次说明不能将市场风险和流动性风险进行简单相加来测度两者的整合风险。此外，我国股市的市场风险与流动性风险的相关性在大部分情况下均大于0，从而说明我国股市市场风险与流动性风险的正向相关性更强，也就是说当市场的流动性风险增大时，市场风险也会相应增大。于是，再次说明研究市场风险与流动性风险的整合风险是很有必要的，而且在研究市场风险与流动性风险的整合风险时，不考虑两者之间的相关结构是不严谨的。

（五）整合风险VaR测度方法的Back-testing检验结果及分析

基于市场风险与流动性风险的相关结构，本文采用蒙特卡洛模拟方法来测度出整合风险的VaR值，并运用Kupiec和Christofersen返回测试方法对模型的稳健性进行检验，各模型的检验结果如表7所示。需说明的是，表7所示的检验结果是对经过5000次蒙特卡洛模拟测得的整合风险进行Backtesting检验而得到的结果。

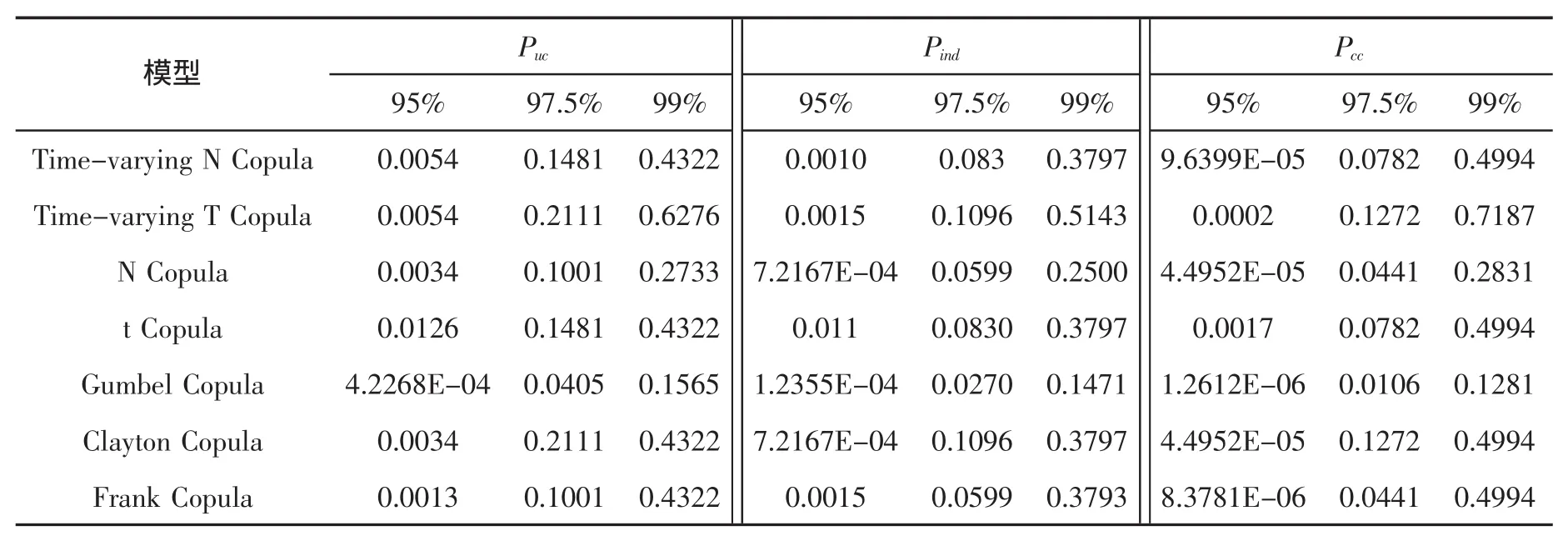
表7 各整合风险测度模型的Back-testing检验结果

从表7中各模型的返回测试检验结果可知：在两种基于时变Copula函数的测度模型中，无论在何种置信水平下，基于时变t Copula函数的测度模型其检验结果均比基于时变正态Copula函数的测度模型所得的检验结果更为优越，这说明运用具有厚尾性的学生t分布比运用正态分布更能捕获市场风险因子及流动性风险因子的尾部信息，进而使得风险测度更为准确。这与流动性风险因子及市场风险因子为“有偏”的特征检验结果相符，同时与江红莉等得出时变t Copula模型优于时变正态Copula模型的研究结果一致。

此外，在5种基于静态Copula函数的风险测度模型中，只有在95%的置信水平下，基于t Copula函数的测度模型的检验结果优于基于Clayton Copula函数的测度模型所得的检验结果，在其他置信水平下，基于Clayton Copula函数的测度模型其检验结果均优于其他模型的检验结果。这说明中国股市流动性风险与市场风险在下尾的相关性较强，即说明当市场严重缺乏流动性导致流动性风险增大时，市场风险也将增大。这与张蕊等得到的中国股市流动性风险与市场风险在下尾的相关性较强的结果一致。

当然，从本文所选的模型来看，基于时变t Copula函数的风险测度模型其Back-testing检验结果在所有模型中的表现最好，说明运用时变t Copula函数对中国股市市场风险与流动性风险的相关结构进行刻画，更能准确测度两风险的整合风险。

基于以上实证结果及分析可知，在对中国股市市场风险和流动性风险之间的相关结构进行考察时，时变t Copula函数不仅比各静态Copula函数更好，而且同样比时变正态Copula函数更能准确刻画两风险的相关结构。另外，就整合风险测度模型的检验结果而言，基于时变t Copula函数的风险测度模型不仅比基于静态Copula函数的风险测度模型更能准确测度整合风险，而且也比基于时变正态Copula函数的风险测度模型在测度整合风险上更为优越，是测度我国市场风险与流动性风险整合风险的最优模型。

四、结论

本文针对当前研究流动性风险与市场风险的整合风险时并未考虑两者相关结构的问题，引入2种时变Copula函数及5种静态Copula函数来刻画两者的相关结构。在运用ARMA-t模型及GARCH-t模型分别对流动性风险因子和市场风险因子的边缘分布进行估计后，再运用Copula函数对两风险因子的相关结构进行考察，进而运用蒙特卡洛模拟法测度出整合风险的VaR值，最后运用规范的返回测试检验方法对模型的稳健性进行检验，得到相关结论如下：

1.通过对中国股票市场风险与流动性风险的相关结构进行考察，得出中国股市的市场风险与流动性风险并非完全正相关，因而如果不考虑两者之间的相关结构，直接将两风险进行简单相加来测度整合风险，则可能出现不准确的风险测度结果。

2.通过对中国股市市场风险与流动性风险的相关结构进行考察，发现中国股市市场风险与流动性风险的相关结构更符合于动态的相关结构，而且这种动态的相关结构，能够用时变t Copula函数进行准确地刻画。

3.在对考虑了相关结构之后的整合风险进行测度时，基于时变t Copula函数的风险测度模型不仅优于基于静态Copula函数的风险测度模型，而且同样比基于时变正态Copula函数的风险测度模型更能准确测度市场风险与流动性风险的整合风险。

由以上结论可知，投资者及风险管理者要实现有效地管理我国股市市场风险与流动性风险的整合风险，则不仅不能忽略两风险之间的相关结构，而且还必须对两者的相关结构进行准确刻画，从而才能更为准确地测度整合风险，进而实现对整合风险的有效管理。当然，对于要维护金融市场稳定和健康运行的我国市场监管者而言，亦是如此。

［1］张蕊，王春峰，房振明，梁葳.市场风险与流动性风险整合风险度量研究［J］.北京理工大学学报（社会科学版），2010（15）：18-22.

［2］Bangia A，Diebold F，Schuerman T，Stroughair J.Modeling liquidity risk，with implications for traditional market risk measurement and management.Working Paper，University of Pennsylvania，December 21，1998.

［3］Angelidis T，Benos A.Liquidity Adjusted value-at-risk Based on the Components of the bid-ask Spread［J］.Applied Financial Economics，2006，16（11）：835-851.

［4］刘晓星，邱桂华.基于买卖价差的我国股票市场流动性调整的风险价值研究［J］.当代经济管理，2008（8）：83-87.

［5］张金清，李徐.流动性风险与市场风险的集成度量方法研究［J］.系统工程学报，2009（2）：154-172.

［6］张尧庭.连接函数（Copula）技术与金融风险分析［J］.统计研究，2002（4）：48-51.

［7］Cherubini U，Luciano E，Vecchiato W.Copula method in Finance［M］.Chichester：John Wiley，2004.

［8］江红莉，何建敏，胡小平.基于时变Copula的La-VaR测度研究［J］.重庆大学学报（社会科学版），2013（3）：27-32.

［9］张铮，李怡宗，张玉龙，刘翔.中国股市流动性间接指标的检验——基于买卖价差的实证分析［J］.经济学（季刊），2013（1）：233-262.

［10］Andreas A，Timotheos A.Idiosyncratic Risk，Returns and Liquidity in the London Stock Exchange：A Spillover Approach，2008.http：//ssrn.com/abstract=1083997.

［11］王明涛，庄雅明.股票市场流动性风险计量模型研究［J］.中国管理科学，2011（2）：1-9.

［12］林宇.基于双曲线记忆HYGARCH模型的动态风险VaR测度能力研究［J］.中国管理科学，2011（6）：15-24.

［13］Kupiec P.Techniques for Verifying the Accuracy of Risk Measurement Models［J］.Journal of Derivatives，1995，（3）：73-84.

［14］Christoffersen P F.Evaluation Interval Forecasts［J］.International Economic Review，1998，39（4）：841-862.

［15］Loebnitz K.Market Liquidity Risk：Elusive No More Defining and Quantifying Market Liquidity Risk［D］.Twente University，2006.

［16］林辉.流动性调整的风险价值模型及其实证研究［J］.科技与经济，2010（2）：93-96.

［17］Giot P.Market Risk Models for Intraday Data［J］.European Journal of Finance，2005，11（4）：309-324.

［18］Patton A J.Modeling Time-varying Exchange Rate Dependence Using the Conditional Copula［R］.Department of Economics，San Diego，University of California，2001.

［19］Patton A J.Modeling Asymmetric Exchange Rate Dependence［J］. International Economic Review，2006，47（2）：527-556.

（责任编辑：卢艳茹；校对：龙会芳）

F830.9

A

1006－3544（2015）02－0054－08

2015-01-07

国家自然科学基金资助项目（71171025）；四川省软科学研究计划资助项目（2014ZR0093）；成都理工大学“金融与投资”优秀创新团队计划资助项目（KYTD201303）

覃小兵（1990-），男，四川内江人，成都理工大学商学院硕士研究生，研究方向为金融工程、流动性风险；唐晓华（1976-），女，四川广汉人，四川工商职业技术学院讲师，研究方向为国际贸易与风险管理；林宇（1973-），男，四川仪陇人，博士，成都理工大学商学院副教授，研究方向为金融风险管理、金融市场与公司理财。