逆城市化及乡镇公共品最佳供给模型分析

沈双生，巩潇然

（河北金融学院，河北 保定 071051）

经济论坛

逆城市化及乡镇公共品最佳供给模型分析

沈双生，巩潇然

（河北金融学院，河北 保定 071051）

乡镇作为人口城市的起点和逆城市化的终点，在人口双向流动的过程中都具有重要地位。尽管逆城市化现象在目前才刚刚开始，由纯农与非纯农人口构成的乡镇最佳人口规模与公共品最佳供给模型分析表明，非纯农人口构成乡镇与纯农业人口乡镇相比，最优城镇人口规模增加，最佳农业人口数量减少，农民的福利得以改善。增加乡镇中的非农业人口，有利于改善乡镇社会公共品供给水平，也是促进乡镇产业转型与经济发展的最佳途径。

乡镇；公共品；供给模型；人口规模

一、逆城市化与乡镇建设

上世纪起，在包括美国与欧洲共同体在内的多数发达国家，逐步出现人口由特大型与大型城市向中小城市和县乡回流的趋势。这一显著的人口分布变化，在相关学术文献中，普遍被称为逆城市化现象。逆城市化理论起源于英国城市学家Ebenezer Howard 1898年提出的“田园城市”概念，他认为城乡一体化的新型社会，有助于缓解城市拥挤、改善环境、降低生活成本、促进乡村发展[1]。近年国外学者针对逆城市化所做的研究多集中在需求方，即研究影响城市居民到乡村居住需求的社会经济学因素。Irwin等人在2010年提出的观点，“自然资源便利是导致美国逆城市化人口迁移的重要因素”，成为这些研究的典型代表[2]。

2006年开始，我国城市化进程的加快带来的城市人口膨胀、地价上涨、交通拥堵、环境恶化、市民生活和居住成本升高等因素所造成的“大城市病”在中心城市和一线城市频现，甚至出现了“逃离北上广”等现象，标志着中国从特大城市开始，逐步进入逆城市化阶段。针对这一严峻的现实，国内学者针对中国城市化高速发展中所带来的诸多问题，也开始逆城市化的相关探索，就经验描述、事例分析和城市病带来的社会现象等方面进行推论与探讨性研究。目前，缺乏系统性的供给方特征和模型，定量分析逆城市化影响小城镇与县乡特征的相关理论性研究报道[3]。

乡镇作为人口城市化的起点和逆城市化的终点，在人口双向流动的现代化社会中都具有重要地位。尽管逆城市化现象目前在我国尚不普遍，但随着我国人口城市化进程的加快，城市吸纳能力和劳动力供给矛盾的加剧，以及城乡一体化程度提高和乡镇就业、生活条件的逐步改善，逆城市化现象将会与经济发达国家一样，规模会不断扩大。因此，我国的乡镇建设不仅要考虑如何有效承接农村剩余劳动力转移，也要考虑吸纳逆城市化的人口转移。

二、乡镇最佳人口规模与公共品最佳供给模型与分析

中国乡镇的发展在经历千百年的自然发展与变迁的过程中，既受人文历史因素的影响，更受到经济与自然的影响，进入商品社会后，经济的影响更加显著。为适应经济发展和农村剩余劳动力转移的需要，我国当前正在大力推进城镇化建设。在建设过程中，如何提高城镇的经济中心功能、文化中心功能和服务功能，使城镇居民能安居乐业，是需要关注的核心问题。为此，本文专门探讨乡镇的最佳人口规模和公共品最佳供给水平。本文将这些乡镇归纳成两种：纯农民居住的乡镇和农民与非农业人口混居的乡镇（即非纯农人口乡镇）。在乡镇的归纳处理中，不考虑农业人口与非农人口的比例对参数的影响。

本文以两个乡镇为基础进行分析，假设乡镇一的居民全是农民，乡镇二混居有农民与非农业人口，假设两个乡镇在其他方面完全同质，据此推导两个乡镇经济系统的最佳人口规模与公共品最佳供给提供水平，分别建立理论模型。

本研究采用纳什均衡的方法，选取边界条件进行比较，以农业家庭、耕地面积、非农与农业人口等作为计算参数，在建立模型的基础上，运用萨缪尔森规则，推导出城镇最佳人口规模和最佳区域性公共品规模，并对两个城镇的最佳规模进行比较。

（一）模型建立的条件

本模型中，暂不考虑转移支付。乡镇政府作为一个独立的经济实体，为所辖地区提供G个单位的区域性公共品，区域性公共品为辖区内所有居民服务。乡镇一没有非农业人口，乡镇二中居住的非农业人口用Nu表示；无论是否从事农业活动，所有居民平均承担公共品供应的成本。我国自2009年起已全面取消农业税，但农民依然缴纳消费税等间接税[4]，模型假设符合我国现实情况。

当区域性公共品的供给水平固定为G个单位时，成本大小取决于乡镇政府辖区内的人口N（= mNa+Nu=Nf+Nu）与辖区大小。随着辖区大小的增长，运输成本等因素也增加，进而使总成本增加。由此可知，区域性公共品成本函数CR（G，N，）与所有参数有正相关关系。对于给定的G与，平均成本函数CR（G，N，）是N的一个U型函数，最小值为N*，并假设N*＞Nf，如图1所示。

（二）纯农业人口乡镇的模型建立与分析

假设乡镇辖区内人口总数N全是农民，即Nu= 0，Na=N/m⇒l=/Na=m/N。每一个农业居民个体的效用，一部分由对复合商品的消费产生，可以用表示；另一部分则由乡镇内其他居民共同消费的U个单位区域公共品产生，可用U（G）表示，U（G）是一个凹函数，并且具有连续递增与二阶可微的性质。综合两部分，得出一位典型农民的效用币值函数（G）。对于乡镇一的政府而言，最优化问题可以用以下公式表达：

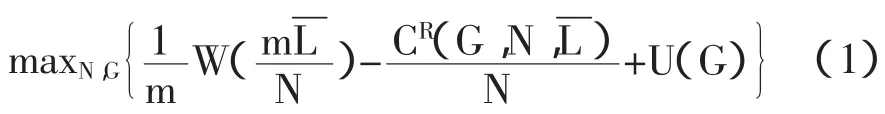
假设存在内部解，需要满足的一阶必要条件是：

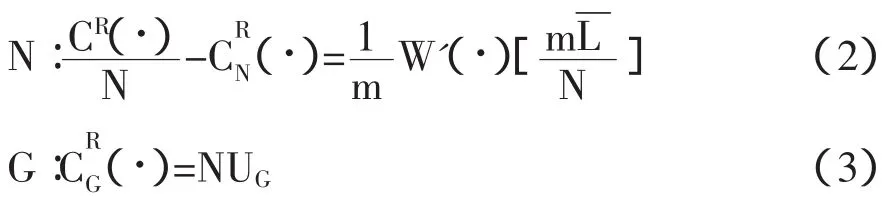
结合图1可知，N*＞Nf的假设表明了只有当时，条件（2）才成立。换言之，为了取得规模经济效益，乡镇一的最佳人口规模（用N0表示，N0＜mNa），达不到使农业生产活动平均成本最小的程度。条件（3）则体现了新古典理论框架下，萨缪尔森规则决定了公共品的最佳供给规模是G0。

上述分析建立在一个隐含假设上，即居住用地不影响区域内可耕地面积。这一假设对于理论分析结果不产生影响。具体而言，将居住用地排除在耕地之外，耕地面积由下降到=-hNa，此处，＞hNa，h代表Na个农户中每一户占用的居住用地，以公顷计。用W（m/N-h）代替W（m/N）代入最优化问题公式（1）中，推导对应的一阶条件（2）、（3）式，对（2）、（3）式不产生影响，对N与G最优值的影响甚微。

（三）非纯农人口乡镇的模型建立与分析

假设乡镇由农民与非农业居民构成，并且除了有是否从事农业活动的差别外，乡镇内所有居民具有同质的其他属性，平均承担区域性公共品的成本，并在使用区域性公共品的过程中获得相同的效用。在这些假设条件下，该乡镇面对的最优化问题，即在给典型非农业居民留存保留效用水平e的前提下，选择区域性公共品供给水平与乡镇人口规模，使典型农民实现效用最大化。这一最优化问题，可以用如下公式表示：

式中，λ是拉格朗日乘数，I0是代表非农业居民城镇收入的外生变量，mNa是乡镇辖区内的农业人口总数。

假设方程存在内部解，一阶必要条件是：

结合图1可知，条件（5）说明达到该乡镇的最佳人口规模（用N*表示）时，边际成本与平均成本相等，此时乡镇平均运营成本达到最低点。条件（7）与条件（3）相同，决定着乡镇内提供区域公共品的最佳规模G*。条件（6）决定了乡镇内农家数量的最优值，此时每个农家的边际产量为0，收益达到极大值。

与乡镇一的情况一致，此处的分析依然假定一个隐含条件成立，即农民与非农业居民的居住用地，不造成耕地流失。放开这一假定，假设每户农业家庭占用h公顷的耕地居住，每个非农业家庭占用公顷（其中＜h），这会造成耕地减少，由减少至，其中=-hNa-Nu=-hNa-（N-mNa），在此，＞hNa+hNu。用W［/Na-（N/Na）-（h-m）］替代W（/Na），并不会影响条件（5）、（6）、（7）。由此可知，与对乡镇一的分析过程一样，放开居民（农业与非农业）居住用地不影响耕地面积的假设，对于理论分析的结果没有影响。出于简化的原因，下文的分析都建立在这一假设的基础上。

（四）两乡镇各变量最优值的对比分析

前文分析已经得出，由最优化问题（1）（4）的一阶必要条件可知，条件（2）与条件（3）决定着N0与G0，条件（5）与条件（7）决定了N*与G*。为比较N*与N0，对条件（5）与条件（7）加以变形，写成如下形式：

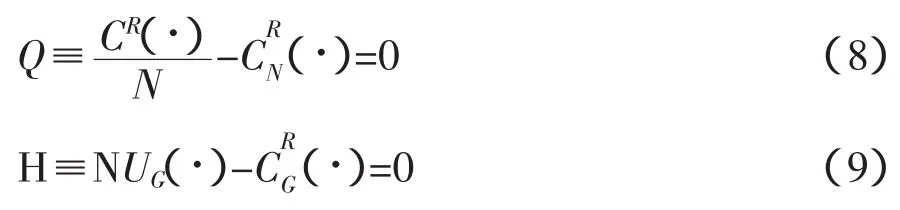
最优化的二阶条件需要满足以下三个条件：

结合函数（8）与（9），将G对N求导，得到：

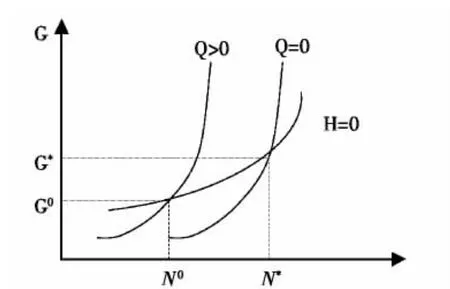
图2 时的最佳组合（N，G）

图3 时的最佳组合（N，G）

除此之外，在乡镇一中，W'（·）＞0，但乡镇二的W'（·）=0。由此可以推导出，进一步得出Na0＞Na*。也就是说，乡镇二中适宜承载的农业家庭数目小于乡镇一。

三、结论

经过对乡镇最佳人口规模与公共品最佳水平供给建立模型与分析，可以得出如下结论；

1．非纯农业人口乡镇的最佳城镇人口规模大于纯农业人口乡镇的最佳城镇人口规模。

2．尽管非纯农业人口乡镇的最佳总人口规模较大，但其最佳农业人口规模小于纯农业人口乡镇的最佳农业人口规模。

3．非纯农业人口乡镇的农民总效用水平优于纯农业人口乡镇。这说明，在乡镇最大限度地吸引非农人口，是改善乡镇人均社会公共品占有水平的有效手段。

［1］霍华德．明日的田园城市［M］．艾比尼泽.北京：商务印书馆，2000．

［2］IWIN E D，ISSERMAN A M.A century of research on rural development and regional issues［J］.American Journal of Agricultural E－conomics，2010（92）：936-945.

［3］孟祥林，张悦想，申淑芳．城市发展进程中的“逆城市化”趋势及其经济学分析［J］．经济经纬，2004（1）：64-67．

［4］刘乐山，何硕成．取消农业税后的县乡财政困难问题研究［J］．经济体制改革，2005（3）：80-83．

（责任编辑：龙会芳；校对：刘文敏）

F062.6

A

1006－3544（2015）02－0067－04

2015-01-22

2014年度河北省社会科学发展研究课题（2014031417）

沈双生（1963-），男，河北唐山人，河北金融学院教授；巩潇然（1988-），女，河北唐山人，河北金融学院教师。